Yangyang Chen,, Rui Yu, Ya Zhang,, and Chenglin Liu

Abstract—This paper proposes a new distributed formation flight protocol for unmanned aerial vehicles (UAVs) to perform coordinated circular tracking around a set of circles on a target sphere. Different from the previous results limited in bidirectional networks and disturbance-free motions, this paper handles the circular formation flight control problem with both directed network and spatiotemporal disturbance with the knowledge of its upper bound. Distinguishing from the design of a common Lyapunov function for bidirectional cases, we separately design the control for the circular tracking subsystem and the formation keeping subsystem with the circular tracking error as input. Then the whole control system is regarded as a cascade connection of these two subsystems, which is proved to be stable by input-tostate stability (ISS) theory. For the purpose of encountering the external disturbance, the backstepping technology is introduced to design the control inputs of each UAV pointing to North and Down along the special sphere (say, the circular tracking control algorithm) with the help of the switching function. Meanwhile, the distributed linear consensus protocol integrated with anther switching anti-interference item is developed to construct the control input of each UAV pointing to east along the special sphere(say, the formation keeping control law) for formation keeping.The validity of the proposed control law is proved both in the rigorous theory and through numerical simulations.

I. Introduction

CURRENTLY, there is increasing interest in the using of a cluster of small unmanned aerial vehicles (UAVs) flying in formation to accomplish some complex missions such as Earth monitoring [1], [2], deep space explorations [3], [4] and oceanographic explorations [5]. In an Earth observing mission, each UAV is desired to fly around Earth with a special orbit and the group is required to maintain formation while responding to relative orbits, which is also called a circular formation flight [6]. Another case is a planetary exploration mission [7], [8], where a formation consisting of numerous spacecrafts is used to enclose a master satellite while maintaining the relative orbit. Some recent experimental results indicate that a formation moving in a bounded space with the predetermined trajectories results in many advantages regarding in mission cost and data collection [5], [9]. Therefore, the design of circular formation flight for UAVs becomes particularly critical.

Previous works have been devoted to disturbance-free motion under the various circumstances in 2D space such as with bidirectional or directed networks, fixed or switching topologies and a geometric variety of curves. In [10], cyclic pursuit formation was analyzed based on a circulant matrix associated with a fixed ring-coupled topology. With the application of Lie groups, [11] applied cyclic pursuit formation with directed networks. However, the circular center in aforementioned references [10], [11] depends on the vehicles’ initial states. To enclose a special center with a circle, Zhanget. al. [12] proposed a geometric solution i.e. the orbit extension method with a fixed and bidirectional network.The result was developed to deal with a set of orbits in[13]–[15] and then bidirectional and switching case in [16].Moreover, there are also a lot of results involving coordinated path following control [17]–[19] based on a leader-following structure. Although the formation trajectories do not focus on simple and closed curves in these works, the ideas developed are still very helpful in the coordinated control problem of circular formation flight.

Nobody can deny the fact that both space missions involving Earth monitoring and deep space explorations involving ocean data collection can be executed by 3D UAVs.Therefore, there is a tendency to develop 2D circular formation algorithms in 3D space. Paley used Lie groups to achieve steady formation motion around a fixed, small circle on a sphere [20] while Zhu showed the consensus equilibria of a high-order Kuramoto model moving on a unit sphere [21].Recently, attitude formation on a sphere has been analyzed with ring topologies [22] and bidirectional topologies [23].The aforementioned references focus on the consensus phenomenon on a sphere rather than the circular formation flight problem. In [24]–[26], so-called master-slave strategies were developed for circular formation reconfiguration of multiple microsatellite systems in Hill’s equations, but the tracking error was difficult to optimize in the presence of disturbances. In [7], the virtual structure approach was presented to address the formation flight problem of 3D particles under bidirectional ring information-exchange topology. To assist with the consensus of adjacent tracking errors, the virtual structure approach was developed in [27] to achieve better robustness and speed of directed coupled UAVs with the second-order dynamics. It is worth emphasizing that the virtual structure approach requires the desired positions and velocities in formation for each spacecraft at all times. To avoid the additional design necessary for the virtual structure approach, a novel method for formation flight based on decoupling the target tracking task and the inter-vehicle coordination task was proposed in [28]. A cooperative control scheme was given for first-order UAVs with the ring-coupled topology [29] and the undirected topology [30]. However, the aforementioned works assume that the motion of each UAV is not affected by the external disturbance and that the networks among UAVs have bidirectional topologies.

As shown in [5], [31], vehicles employed by ocean explorations are inevitably affected by external disturbances(e.g., ocean currents), which often results in poor sampling performance. Another case in point is formation flight [32],where the dynamics of a spacecraft includesperturbations,atmospheric drag, solar radiation pressure and the like.Therefore, it is essential to give a systematic method for robust formation tracking control with external disturbances.When the external disturbances affect each vehicle,disturbance-free circular formation control laws can be easily extended to deal with robust formation movements by adding an input item to counteract the effectiveness of disturbance.The details can be found in [33], [34]. When an external disturbance can be represented as a spatiotemporal variable with an unknown parameter vector, [35]–[41] who that adaptive technology can be applied to achieve circular formation motion in bidirectional networks. However, the disturbances acting on UAV, especiallyperturbations,atmospheric drag and solar radiation pressure, can only generally be regarded as a bounded force [42], [43], which implies that it is difficult to translate them into the parameterized form as in [35]–[41]. To this end, Zhang and Song [44] developed the virtual structure approach with a time-varying nonlinear saturation function to adapt the robust formation flight control law to a bidirectional topology.Recently, a robust formation flight algorithm was proposed in[45] to counteract the bounded disturbances in a directed network. Unfortunately, the conclusion that tracking errors converge to small regions was obtained. Furthermore, it was found that the control parameters required the knowledge of the smallest real part of the nonzero eigenvalue of the Laplacian matrix associated with the directed network (say, a global information of network), which leads to the tremendous disadvantages with the distribution of the controller.Furthermore, the formation flight controllers proposed in [44],[45] inherit the shortcomings of the virtual structure approach.

Motivated by the facts and challenges stated above, the goal of this paper is to develop the circular formation flight control for bidirectional connected UAVs [39] in a directed network with external disturbances. It is worth pointing out that the extension from a bidirectional network to a asymmetric topology is nontrivial due to the fact that it is difficult to select a common Lyapunov function for the latter. To this end, we separately design the control for the circular tracking subsystem and the formation keeping subsystem with the circular tracking error as input. The whole control system can then be regarded as a cascade connection of these two subsystems where its stability is proved by ISS. In contrast with the virtual structure approach [7], [27], [44], [45], the objectives of 3D circular formation flight as illustrated in this paper not only involve determining the tracking motion along each circle on the target sphere, the circular formation in the lateral direction, but also involves the avoidance of each UAV’s trajectory to the set defined by the undefined circular formation in the lateral direction. It should be emphasized that the last objective is also necessary and neglected in [28], [29].Furthermore, the description of the desired trajectory in this paper uses differential geometry, especially the level sphere of the spherical function and the azimuthal angle, which is avoided with the external design for the desired trajectory at each time in the virtual structure approach.

The second contribution of this paper is to give a new robust circular formation flight algorithm to confront the spatiotemporal disturbance with knowledge of its upper bound. Meanwhile our proposed controller does not require any global information of network in the eigenvectors of the Laplacian matrix. Different from the adaptive estimate for uncertain parameterized disturbances under bidirectional networks [35]–[39], three switching functions (say, three sign functions) are brought into the controller design. For the purpose of achieving an asymptotic convergence result of circular tracking instead of the boundedness of the tracking errors as shown in [45], this paper first determines the velocities of each UAV pointing to the North and Down along the special sphere and then the inputs in these two directions by backstepping. In order to avoid the use of global information of network as pointed out in [45], we use the distributed consensus algorithm proposed in [46] to construct the control input of each UAV pointing to East along the special sphere, which ensures the distributed nature of our control in the presence of disturbance. [46] deals with a linear multi-agent system without consideration of disturbances.

The paper is organized as follows: Section II summarizes the control problem of circular formation flight. The main result is given in Section III. Simulation results are presented in Section IV. Conclusions are given in Section V.

II. Problem Formulation

Before representing the definition of the control objectives of circular formation flight, here we introduce another frame named the Earth-centered, Earth-fixed (ECEF) framewhere its originis located at the center of the sphere (e.g., the Earth), itsextends to true north, itsintersects the sphere at the equator and prime meridian in Greenwich, and itscomplies with the right-hand rule. To simplify the coordinated description, we assumeandare parallel to thex-,y- andz-axes of the world framerespectively. It should be noted in particular that the ECEF frame is suitable in building the connection between the geometric patterns of sphere and the objectives of the circular formation flight task. As shown in Fig. 1, each position on a special sphere can be defined by a fixed length, a latitudeand a longitudewheredenotes the one-torus, that is,implies we identifywithThe fixed length can be used to represent the distance from each UAV to the target spherical surface by the spherical function given in Lemma 1. The desired value of the latitudecan be denoted as one circular orbit on the sphere whose center is located at thedue to the fact that any point on the circular orbit responds the same latitude.

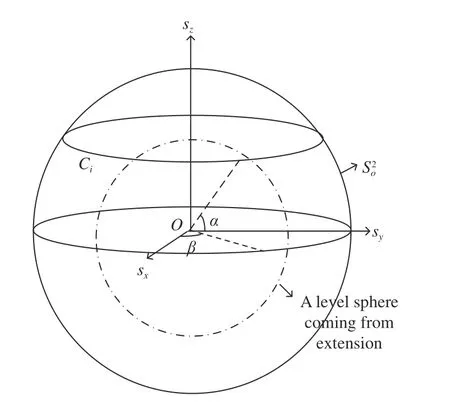
Fig. 1. ECEF frame and circular tracking.

Lemma 1 [39]: Since a spherewith a fixed radiusis a regular compact orientable surface, it can be p(arameterized as a smooth function=Extendingby

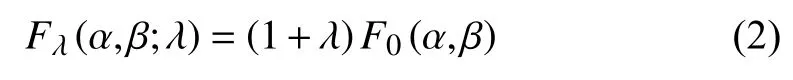
there exists

Remark 1:According to Lemma 1, a simple expression ofis

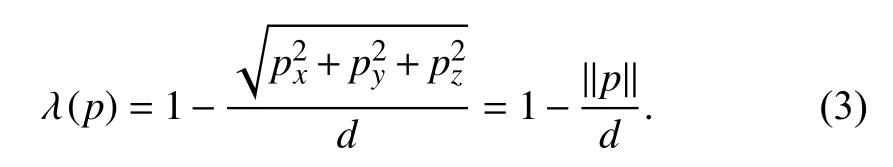
Although Lemma 1 restricts the domain of the sphere function (say, the open set) in the set withdue to the tubular neighborhood theorem on pagein [47], from (3)the boundary parametercan be selected as the value of the fixed radius of the spherein real application.

Note that the calculation of the arc-lengthalong a circle associated with theUAV is based on the longitude(see(22)). In the whole paper, each symbol (e.g.,and the like) with a subscriptdenotes the state associated with theUAV. By referring to the definition of lateral formation flying in [12]–[14], [29], [33]–[39], we apply the description of lateral formation around circles by using the consensus of the generalized arc-lengthwhereis a secondorder continuously differentiable function (say, asmooth function) of the arc-lengthsuch thatandare bounded andfor allIt should be noted that the choice of the generalized arc-length(the abbreviation ofis not unique. In other words, one formation can be applied to the consensus of generalized arc-lengths with different expressions. For instance, three UAVs are moving around various circles on a sphere while maintaining a in-line formation associated with the positions projected onto the equatorial plane as pictured in Fig. 2. To keep the desired formation, we can select the generalized arc-length asordue to the fact thatis equivalent toor in other words, the “inline formation” is achieved when any above equation holds. In order to force each UAV to orbiting around its responding circle with a desired rotation speed, we define a reference generalized arc-lengthwith a constant signal

Remark 2:It is obvious that the generalized arc-length or the arc-length is undefined if the position of one UAV lies inthat isor equivalently its responding latitude=±π/2. Therefore, a movable set for theUAV is defined as

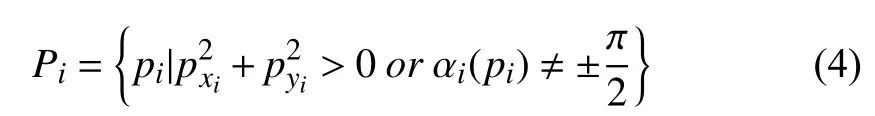
which implies that the trajectory of each UAV should not reach the

For the purpose of achieving the cooperative movement,information exchange between UAVs is essential. Let us revisit some basic definitions on graph theory.

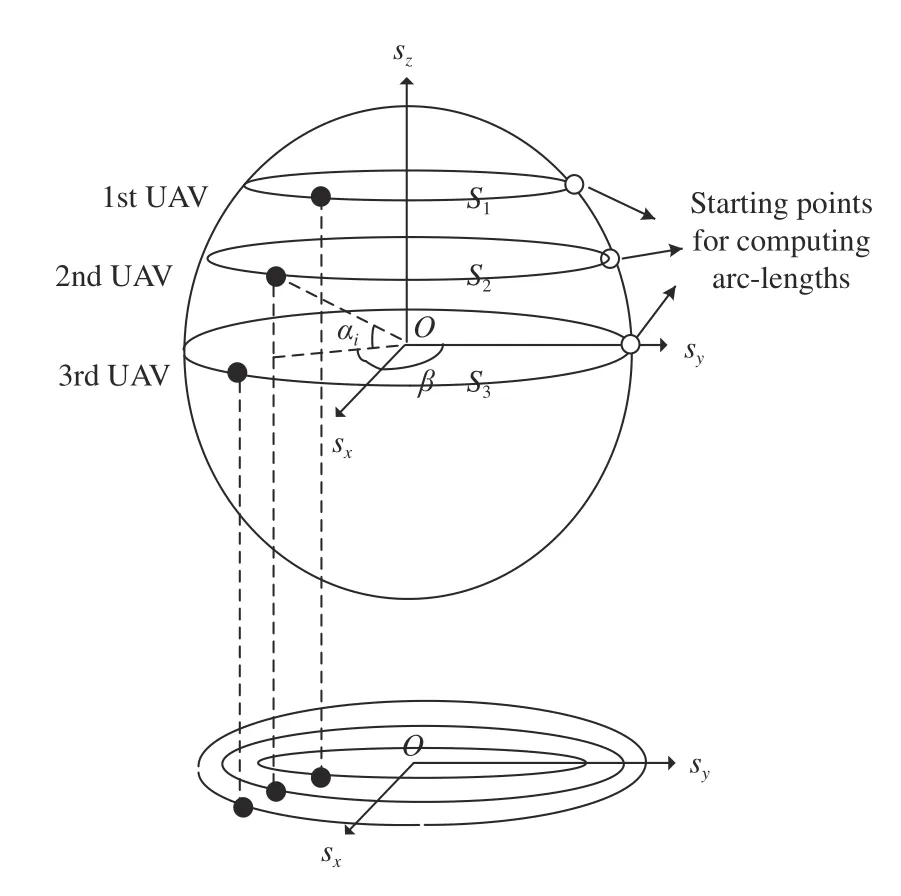
Fig. 2. Circular formation.

be a directed network topology, wheredenotes the set ofUAVs andis a set of data links. An edgedenotes that theUAV can receive information from theUAV. A directed path from nodetois a sequence of edgesin the directed network topology with distinct nodesA directed network topology is called a directed tree if there exists a node called the root node that has directed paths to all other nodes in the graph. Let forifandotherwise. Also define the Laplacian matrixwhereandfor anyFor the purpose of achieving circular formation flight in a distributed manner, let a virtual nodedenote the reference signalIn this paper, only a few of UAVs (at least one) can accessIf theUAV can determinewe letotherwiseUnder Assumption 1, the Laplacian matrixassociated with the directed topology consisting ofUAVs and the virtual node can be represented as

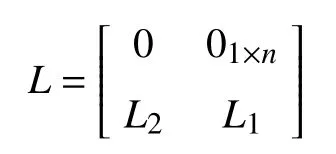
Assumption 1:The directed topology associated withUAVs and the reference signal (say, the virtual node) is fixed and contains a directed spanning tree with the reference signal as the root node.

Assumption 2:The external disturbanceis bounded such aswhereis a known bounded value.

Assumption 3:The center of the target sphere is located atin the ECEF frame and the center of each desired circle is situated at

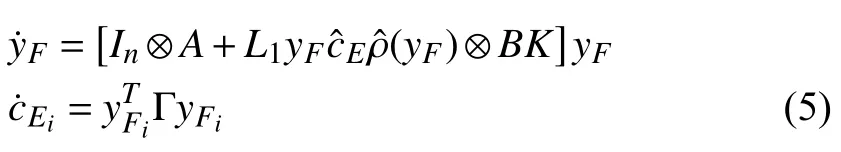
Lemma 2 [46]:Consider a distributed control system wheredenotes the identity matrix of dimensionandare constant matrices with compatible dimensions such that(A,B) is stabilizable,denotes the Kronecker product,is the state vector of the system with arbitrary dimension,is a solution toandUnder Assumption 1, there exists a continuously differentiable function

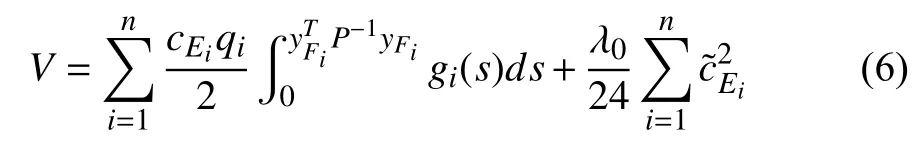
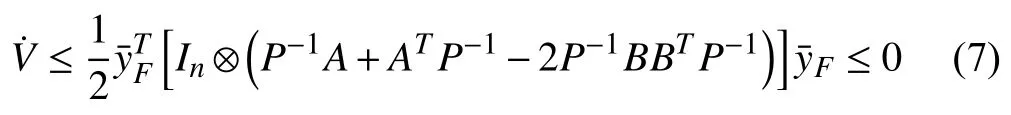
Remark 3:As indicated in [32], [45], the disturbance such asperturbation, atmospheric drag, solar radiation pressure and the like can be generated as a bounded force. Therefore,the disturbance under our consideration is an uncertain bounded force with the knowledge of its upper bound. In[35]–[39], the form of the external disturbance is composed of a known spatiotemporal variable and an unknown parameter vector, which is different from that which is proposed in this paper.

Remark 4:The purpose of Assumption 3 is to simplify the design representation and the expression of control law so that it is not necessary. When the target sphere and each desired circle does not satisfy this assumption, one can rotate and translate the coordinate system to make Assumption 3 valid at first. Then, in the coordinate system after rotation and translation,orcan be calculated and the control law can be designed under our proposed method. Finally, the control law can be represented in the original coordinate system by multiplying the inverse of the responding coordinate transformation matrix.

From the above discussion, the objectives of circular formation flight for each UAV can be summarized as follows:

1) According to Lemma 1, the circular tracking motion on a special sphere is achieved by

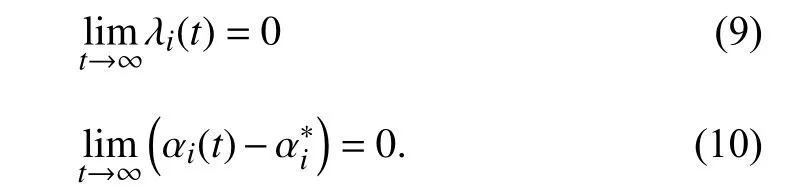
2) The formation keeping motion around a set of circles is achieved if

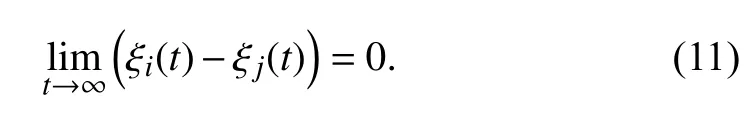
3) Also by Lemma 1, the sphere function is defined on the setwhere the following condition

should be guaranteed for all

4) As indicated in Remark 2, the positions at thelead to an undefinedand we additionally guaranteefor allespecially,

The control objective (9) contributes to the tracking of the special sphere, which implies that each UAV arrives on the special sphere ifthe control objective (10)contributes to the tracking of the desired circle on the sphere,which means that each UAV moves around the given circle when

Now, we give the definition of the circular formation flight control problem with directed network and external disturbance as follows:

Definition 1:Given any initial positionand any radiusof the target sphere, under Assumptions 1–3, find a distributed control law in the form of

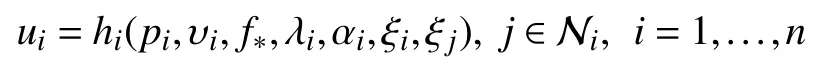
such that (9)–(13) are satisfied.

III. Main Results

A. Coordinated Control Model

Before representing the dynamics of circular tracking errors and formation keeping errors, we introduce three orthogonal vectors defined as follows:

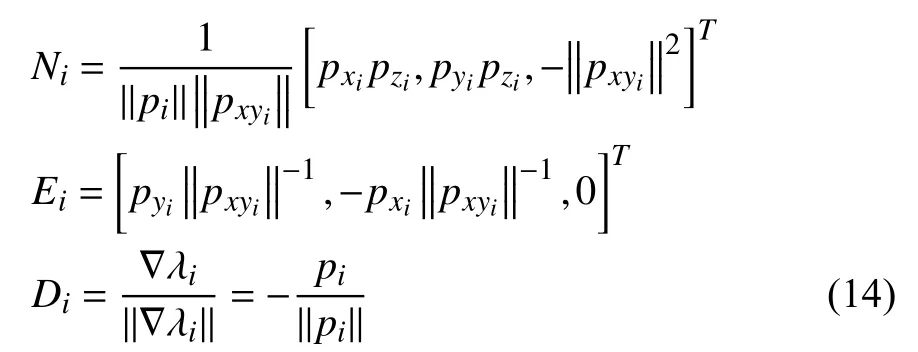
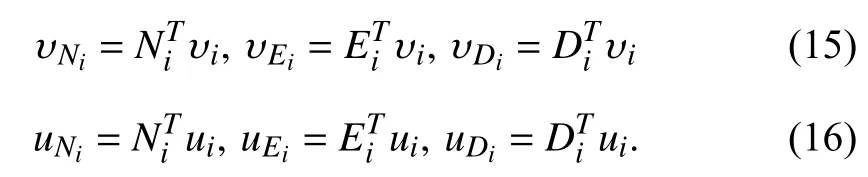
Remark 5:The control objective (13) ensures that the position of each UAV does not reach to the(also see(4)), results infor all the time, which implies thatfor all the time. Therefore, it is indicated thatandin (14) are well-defined by using our potentialfunction-based control law. The details can be found in Section III-B.

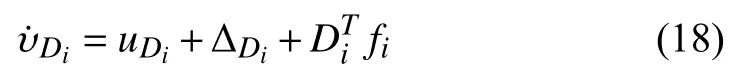
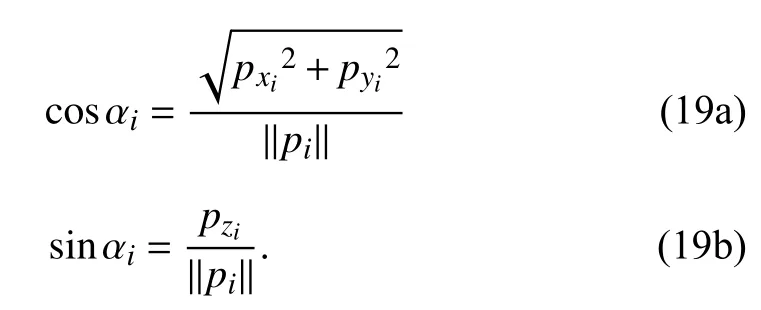
Taking the time derivative of (19b) and then substituting(19a) into it, we have

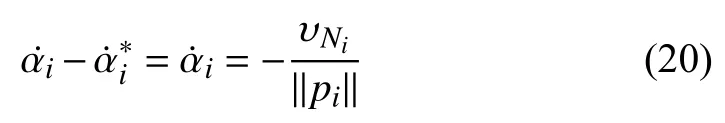
which represents the dynamics of the tracking error of the desired circle on the sphere. Similar to the design process aswe also first regardas a virtual control and then designby backstepping. Therefore, the dynamics ofis given as following:

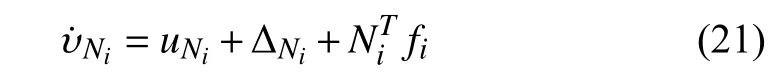
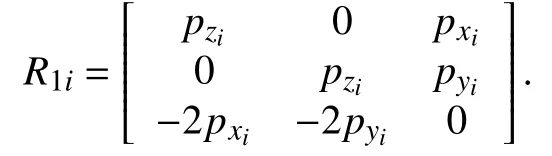
To compute the general arc-lengthlet us give the expression of the arc-length in the beginning, i.e.,

蓝宝石因其通透的深蓝色而得到“天国之石”的美称，早在古埃及、古希腊和古罗马，蓝宝石就被用来装饰清真寺、教堂和寺院，并作为宗教仪式的贡品。高贵纯净的蓝色光芒也让蓝宝石被尊崇为圣职者佩戴的不二选择。

where

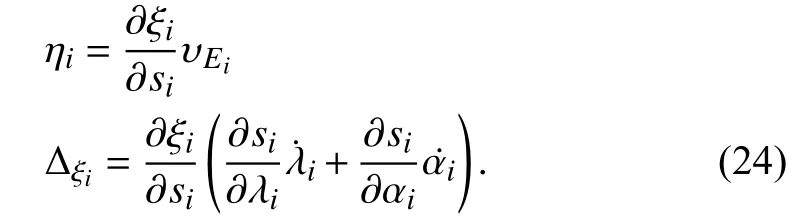
Differentiating both sides of (24) yields

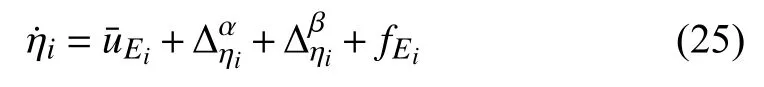
where

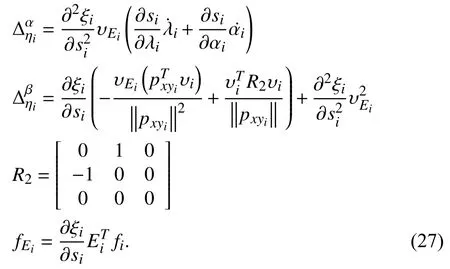
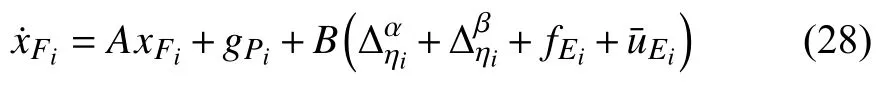
Define

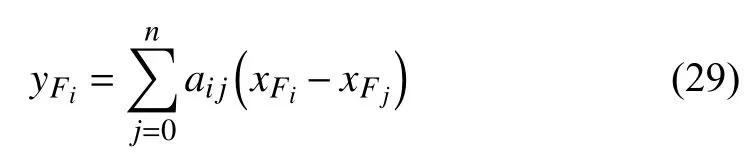
to represent the error of formation keeping for theUAV.From (29), the error of formation keeping for the family can be written as

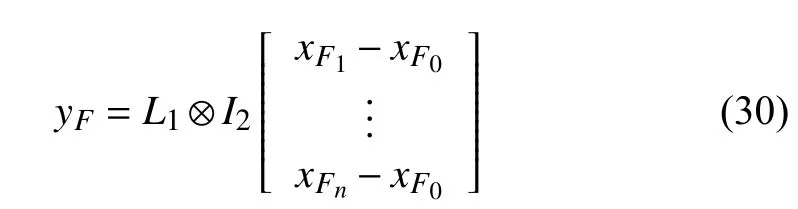
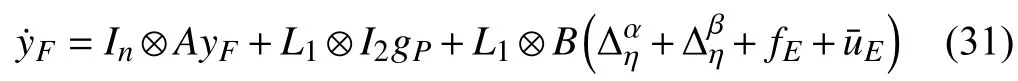
From the above discussion, the error equations for the circular formation flight control system can be summarized as(17), (18), (20), (21) and (31). The first four equations denote the open-loop equations for circular tracking motion on a special sphere (say, the circular tracking subsystem), whereas the last one represents the open-loop dynamics of formation keeping (say, the formation keeping subsystem). It should be noted that the operation of the formation keeping subsystem does not affect the circular tracking subsystem, whereas the formation keeping subsystem is affected by the circular tracking errorsanddue to the fact thatandare two functions ofandTherefore, we separately design the algorithm for the circular tracking subsystem and the formation keeping subsystem and then regard the whole control system as a cascade connection. The design process will be given in the next subsection.

Remark 6:In [22], [23], [28], [30], a simple representation of a formation is built on the longitudeThe reason why this article chooses the generalized arc-lengthto represent the formation is that it is easy to separate the tracking errorsand their derivatives from the formation keeping subsystem as in (28) and (31). Then, we can separately design the control for the circular tracking subsystem and the formation keeping subsystem with the circular tracking error as input. As a result, ISS theory can be applied to prove the stability of the cascade system of these two subsystems. The details can be found in Section III-B.

B. Controller Design

Let us begin with the circular tracking subsystem (17) and(20) and consider the following Lyapunov function

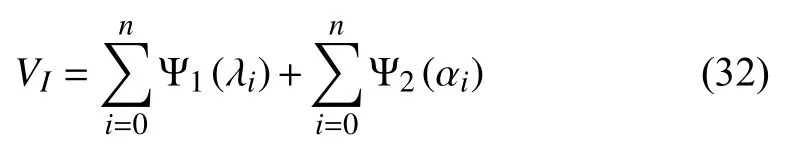
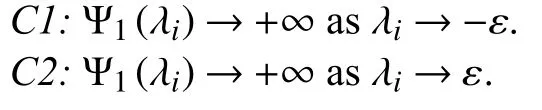
C3:if and only if

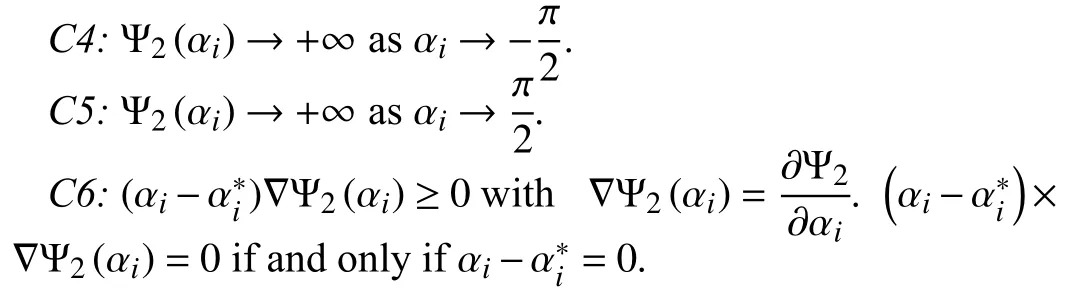
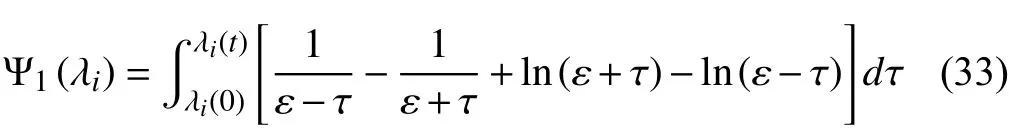
with

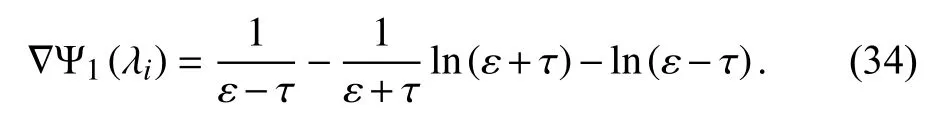
Functions (33) and (34) are depicted in Fig. 3. Similarly, the expression ofandcan be selected as

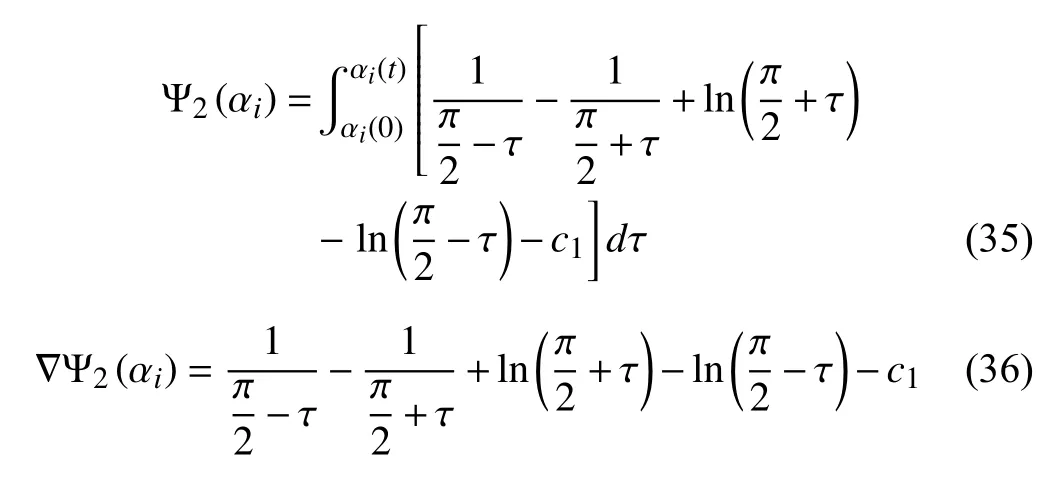
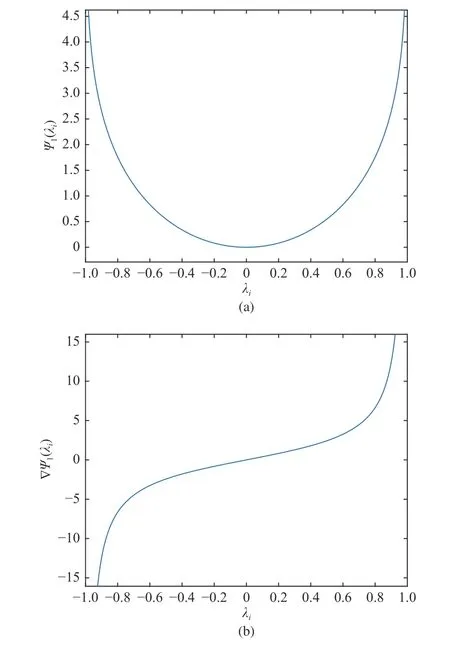
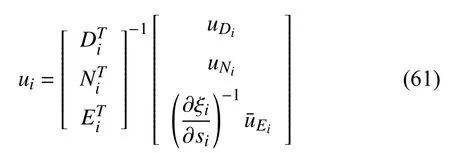
Fig. 3. The function and its derivative: and (b)

Remark 7:Functionsandare usually known as potential functions and used to avoid obstacles in the literature [49]. In this paper, we bring them to ensure the range of each UAV’s motion (12) and (13), respectively.

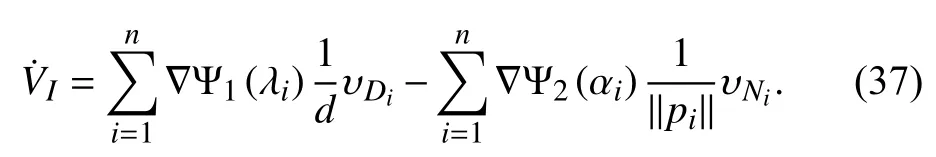
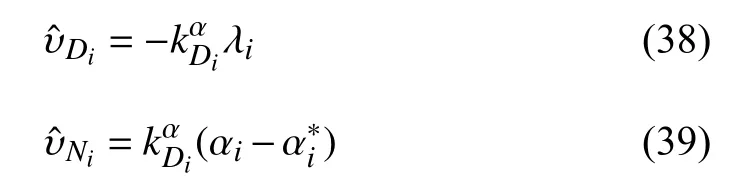
where the control parametersandare greater than

To design the input componentsandwe introduce the error variables

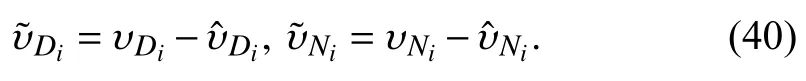
Substituting (38) – (40) into (37) results in

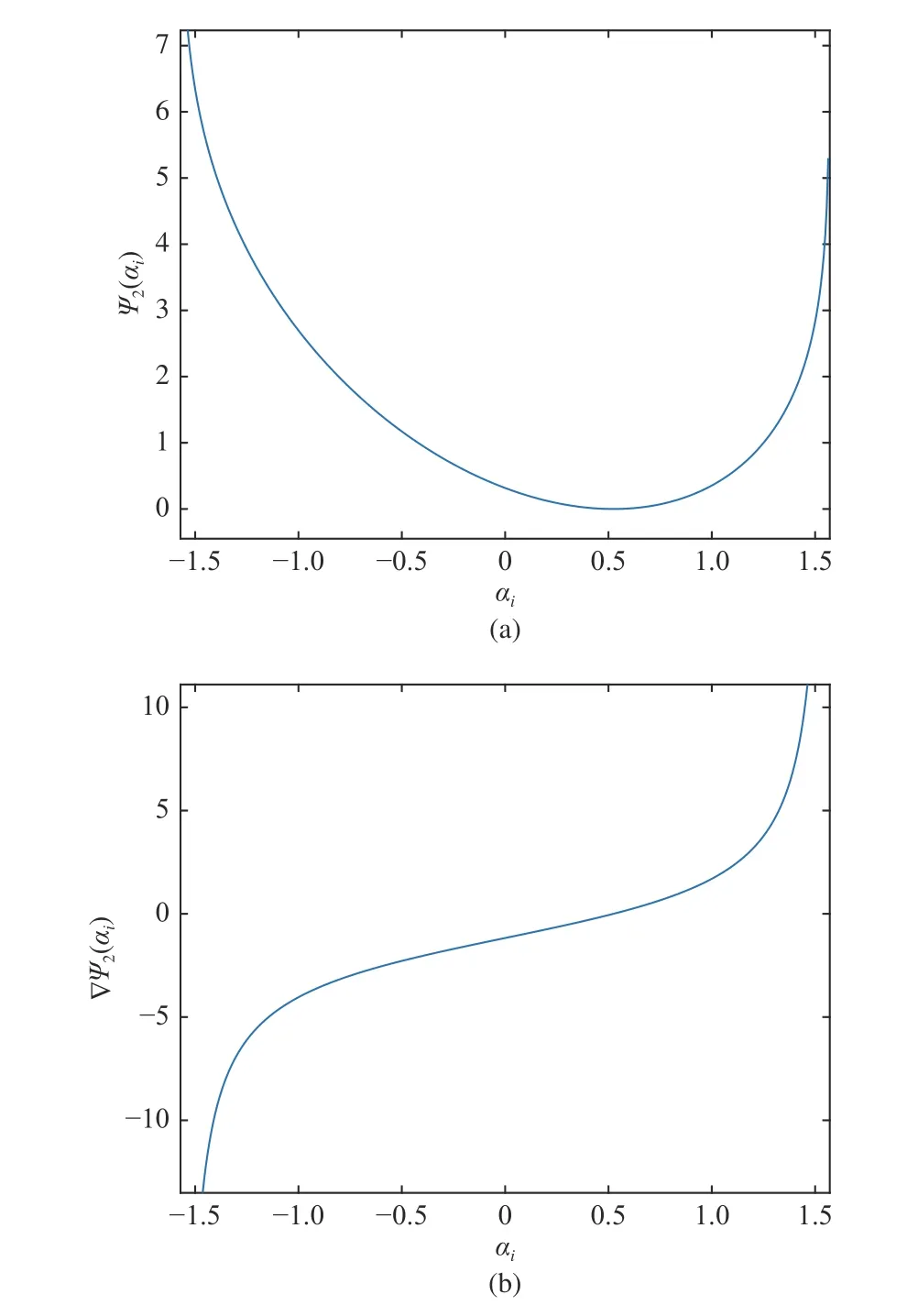
Fig. 4. The function and its derivative: (a) and (b) where

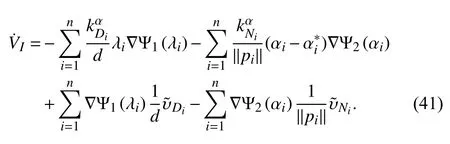
In the following, we will show the design process of circular tracking (i.e.,andby backstepping. The dynamics of the error variablesandshould be given in advance.Differentiating both sides of (40), we have

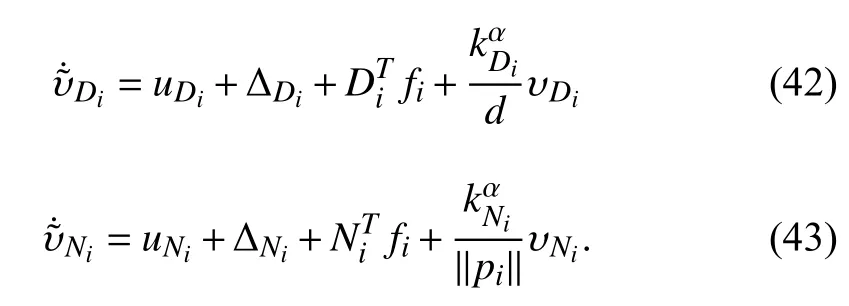
Now, let us consider the following augmentation of the Lyapunov function:

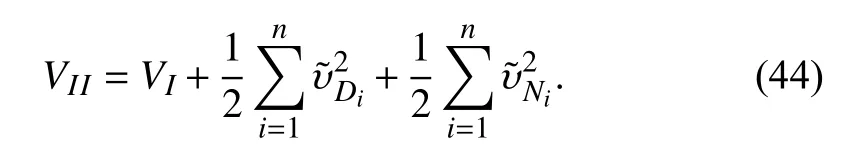
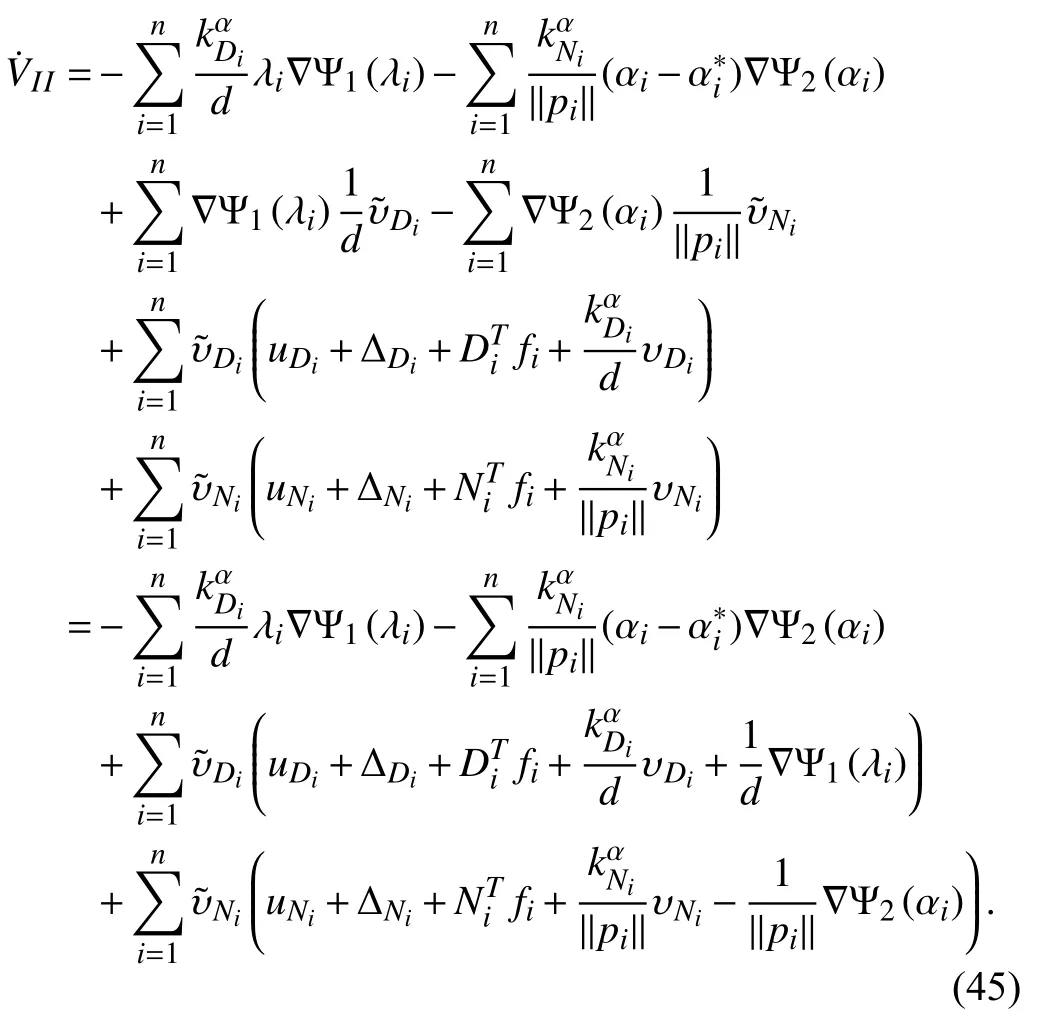
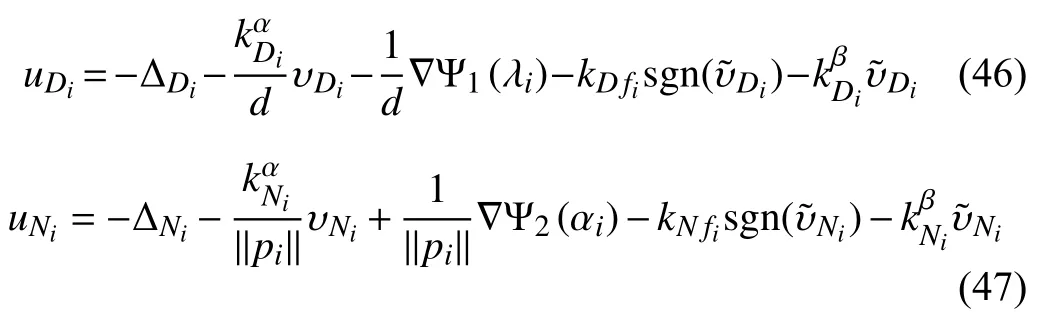
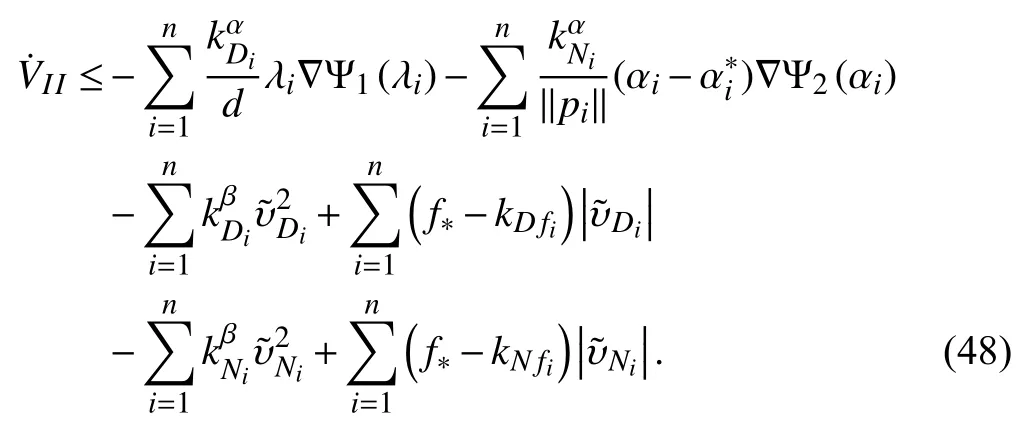
According to the characters of functionand(say, the conditions C3 and C6) as well asandone can easily check thatis negative definite.

Using the circular tracking control laws (46) and (47) with virtual control (38) and (39), the equations of the closed-loop subsystem for circular tracking are denoted as

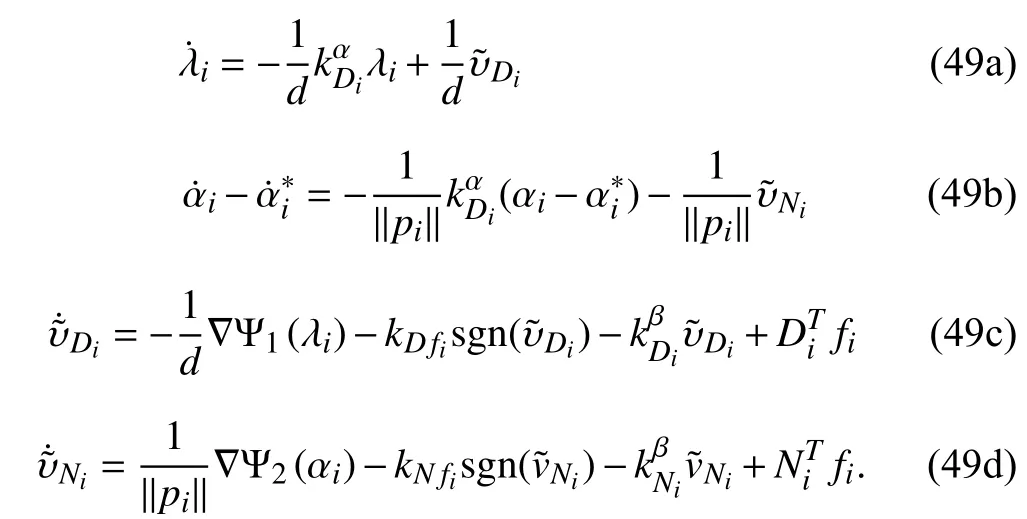
Lemma 3:Given any initial positionand any radiusof the target sphere, under Assumptions 2 and 3, the circular tracking control laws (46) and (47) can guarantee the objectives (9), (10), (12) and (13).

Proof:The setwith the constantis closed by continuity. Sinceandthe setis compact. Then the closed-loop subsystem (49) for the circular following is Lipschitz continuous on the setand a solution exists and is unique. Due tothe value ofis time-independent and non-increasing. Then one can easily conclude that the entire solution stays infor any initial positionwhich implies that (12) and (13) are tenable according to C1, C2 and C4, C5. Applying the Lyapunov stability theorem, we have

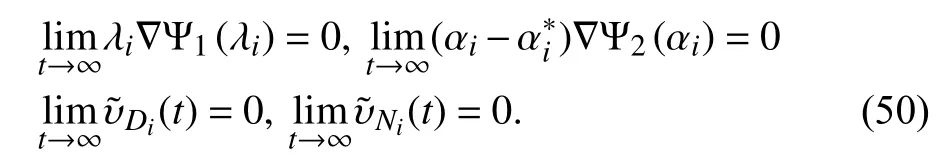
According to the conditions C3 and C6, from (50) it follows that the objectives (9) and (10) are satisfied by our proposed circular tracking control laws.

From Lemma 3, the circular tracking control algorithms(46), (47) forceto converge to zeros finally, which implies the asymptotical convergence ofandTherefore, we firstly consider the formation keeping subsystem by neglectingand

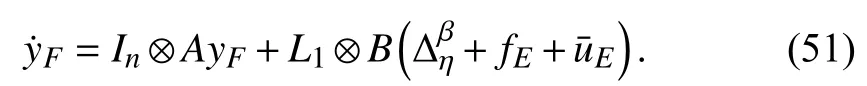
Still, the simplified system (51) is affected by the external disturbanceTherefore, we cannot directionally apply the similar consensus protocol given in [46] to achieve the formation objective (11), i.e.,

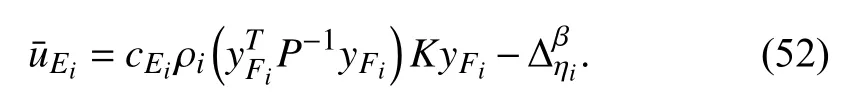
Note that under (52) the closed-loop subsystem of formation keeping becomes

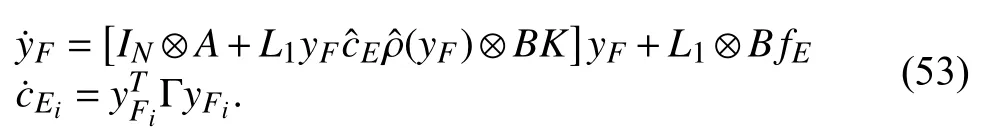
Compared to the distributed control system (5), the only additional termappears in (53). Therefore, anther control item is required to integrate into (52) to form our formation keeping control law, i.e.,

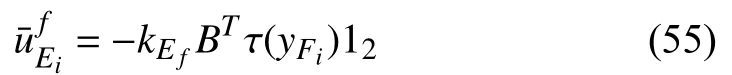
Remark 8:Neglectingandin the formation keeping subsystem can greatly reduce the difficulty and complexity of the design of the formation keeping control law.

Lemma 4:Given any initial positionand any radiusof the target sphere, under Assumptions 1–3, the objectives of formation keeping (11) is achieved by the control law (54) with the adaptive control lawas shown in the second equation of (5).

Proof:Let us consider the formation keeping subsystem(51) and the augmentation of the Lyapunov functionin the form of (6). The derivative ofis

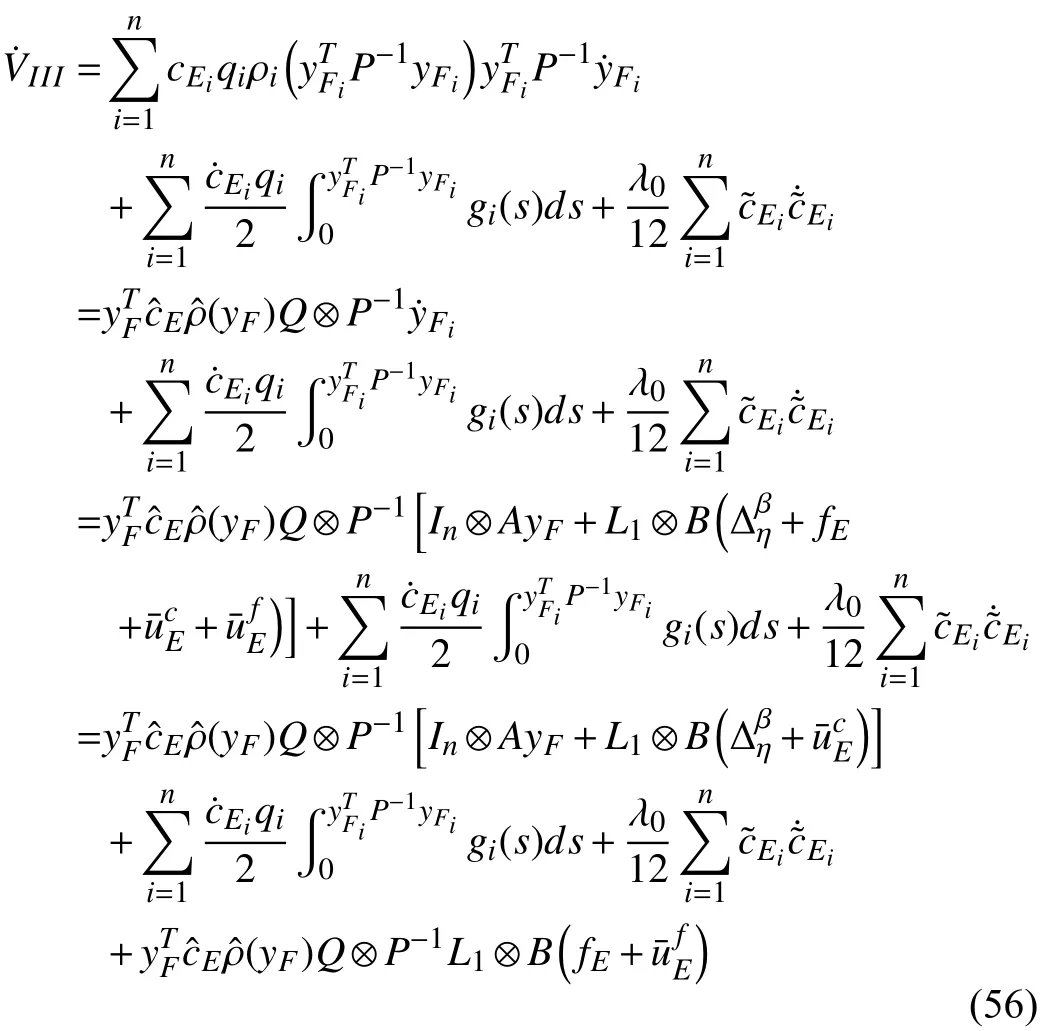
By referring to Lemma 2, with the control lawwe have

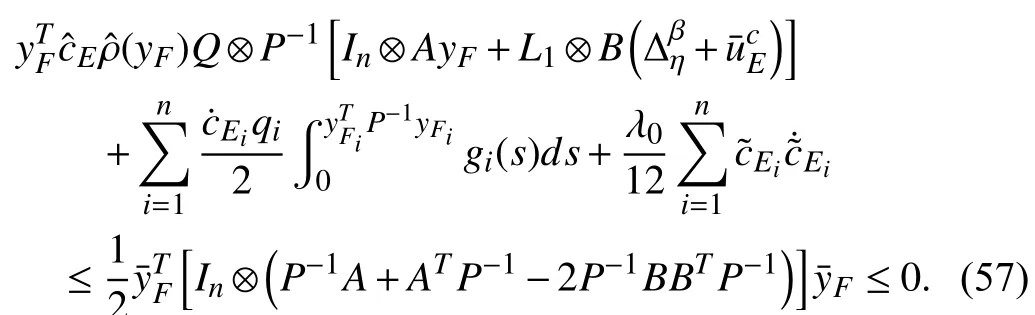
In the following, we will show thatSincecan be represented aswithfrom (55) we have

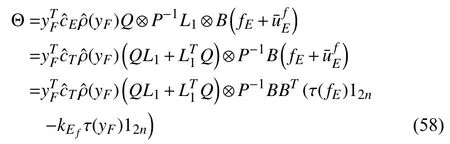
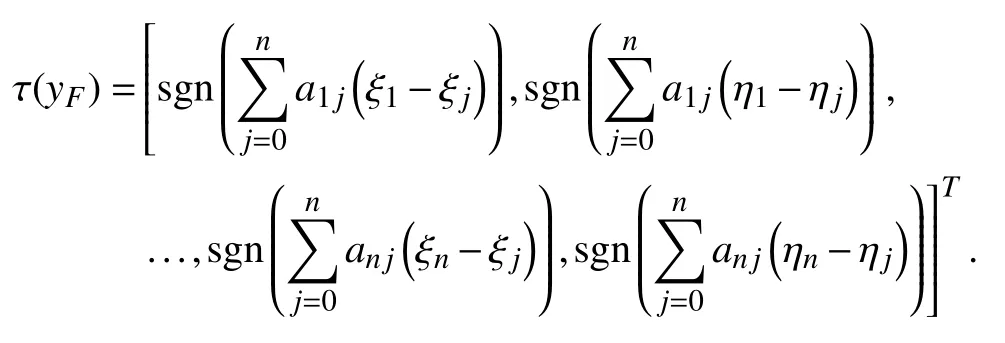
According to (56), (57) and (59), we have

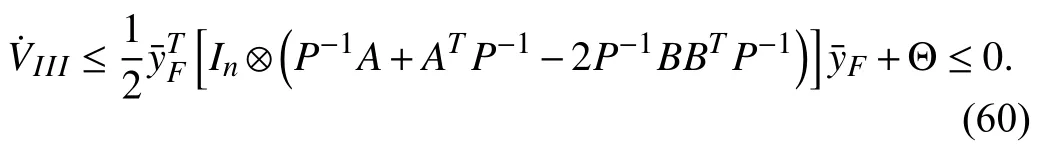
By using LaSalle’s Invariance principle, it follows thataswhich implies thatasFrom (29), it is obvious that (11) is tenable. ■

Remark 9:Note that the definition of symbolin (29) is only established based on theUAV’s stateand its neighbors’ informationThe formation keeping control law (54) comprised of (52) and (55) with the adaptive controlis designed without using any global information.Meanwhile, the control parameters in (54) are irrelevant to the Laplacian matrixorTherefore, our proposed control law is fully distributed in contrast to [45].

Through the analysis of the circular tracking subsystem and the formation keeping subsystem, we can obtain the main result based on the ISS theory for the cascade system.

Theorem 1:Given any initial positionand any radiusof the target sphere, under Assumptions 1–3, the circular formation flight control problem defined in Definition 1 is solvable via the distributed control law

Proof:According to Lemma 3, we conclude thatandcan accomplish the objectives of circular tracking (9), (10),(12) and (13). Thenandare bounded and asymptotically disappear. Ignoringandfrom Lemma 4, the closed-loop subsystem of formation keeping (51) is asymptotically stable and thus the formation keeping subsystem (31) under control law (54) is ISS from Lemma 5.4 on page 219 in [50]. Then the whole control system as a cascade connection of the circular tracking subsystem and the formation keeping subsystem is asymptotically stable by referring Lemma 5.6 on page 221 in[50]. ■

Remark 10:Although we only consider the circular formation flight control problem on the same sphere with radiusit is worth mentioning that our design can be extended to the case of different spheres by replacingwithin the control (46).

IV. MATLAB Simulation

In this section, the performance of our proposed control law is evaluated by MATLAB simulations. The directed network is depicted in Fig. 5 and only theUAV can obtain the reference signalwith

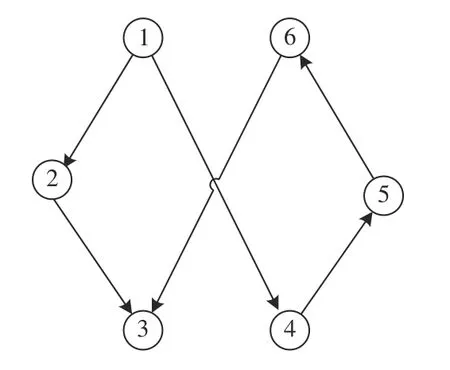
Fig. 5. The directed network.

The radius of the target sphere isand the external disturbance iswith its boundThe latitude associated with each desired circle on the sphere is

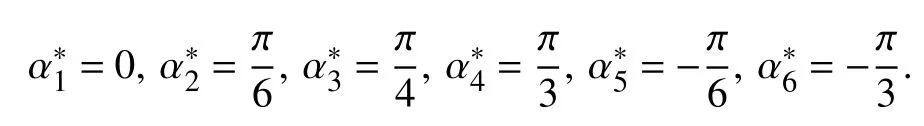
It is necessary that four UAVs fly in the same azimuth angle so that the generalized arc-lengths are selected asAs indicated in Remark 4, we selectThe initial position and velocity of each UAV are listed as follows:

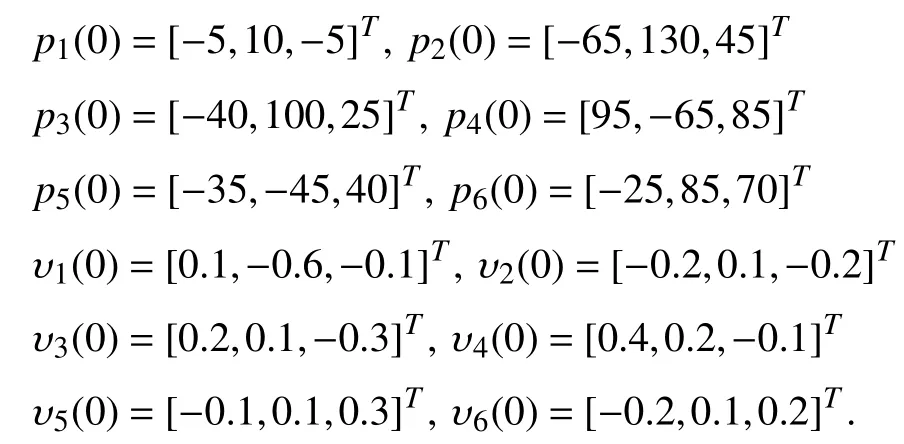
According to Lemmas 3 and 4, the control parametersare required to be greater thanwhere the control parameterTherefore, the control parameters are selected as

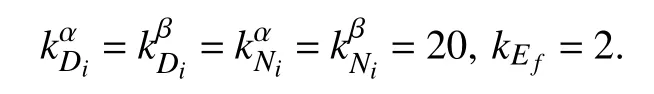
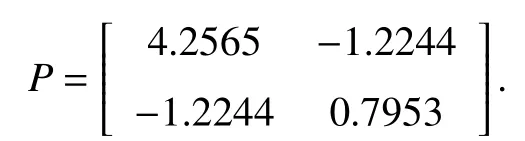
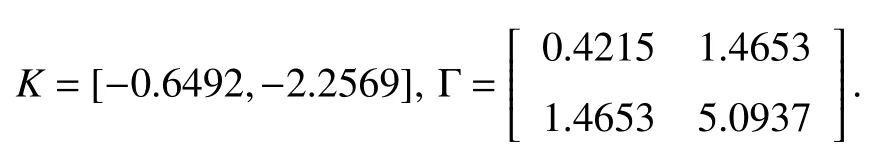
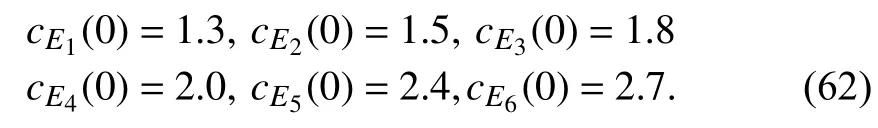
The trajectories of all agents are shown in Fig. 6, where the symbol “denotes the positions of all agents atFrom this picture, one can obviously see that each UAV finally flies around its corresponding orbit on the given sphere and the family keeps the desired formation.The error of circular trackingplotted in Fig. 7 shows thatis limited infor all the time and approaches zero, which indicates that the objectives (9) and(12) are achieved. Meanwhile, Fig. 8 shows thatconverges toand never reacheswhich implies that the objectives(10) and (13) are also achieved. Fig. 9 demonstrates thatreaches a consensus, i.e. the lateral formation is maintained.All of the figures imply that the robust circular formation flight control problem can be achieved via our proposed method when the network is directed.

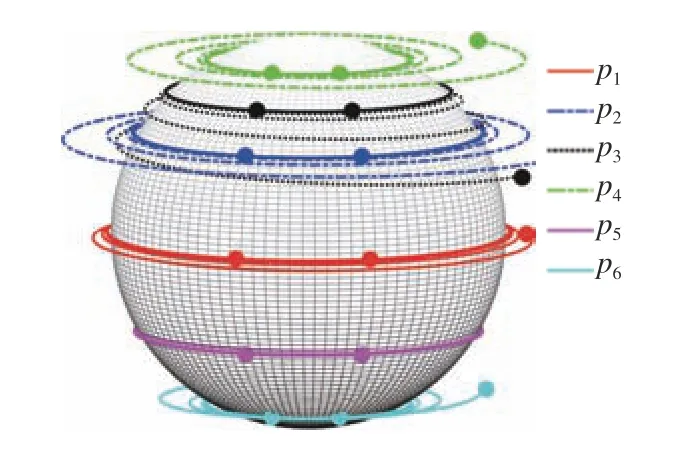
Fig. 6. The trajectories of UAVs.

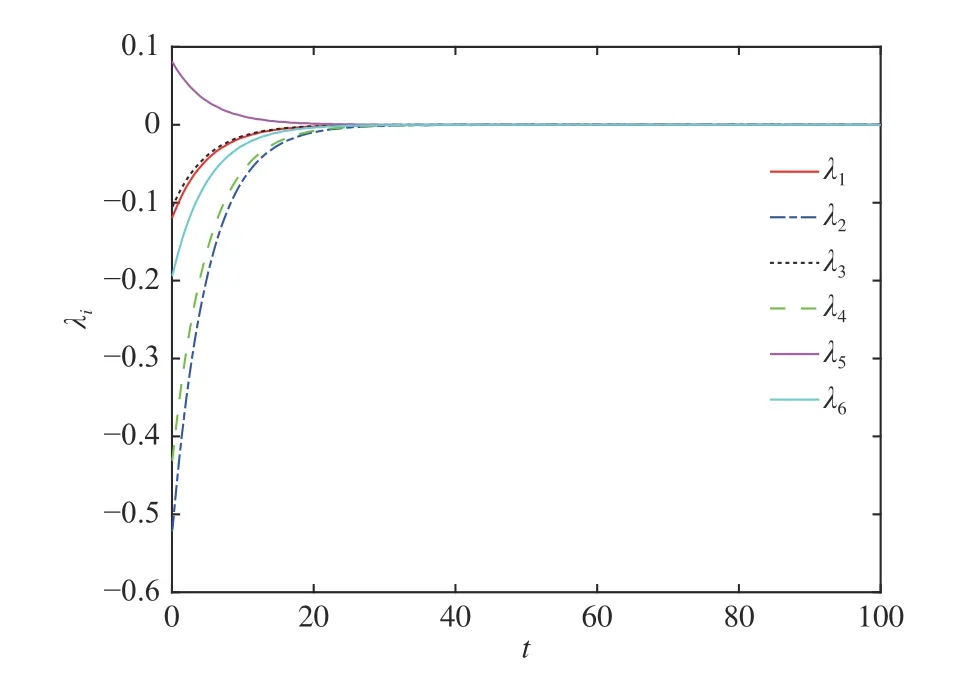
Fig. 7. The plot of

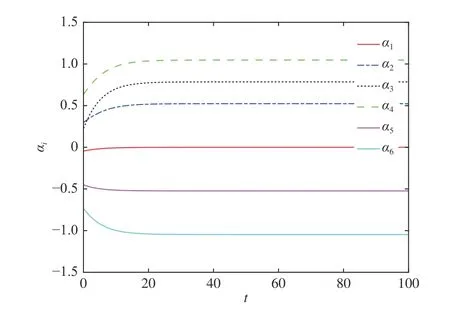
Fig. 8. The plot of

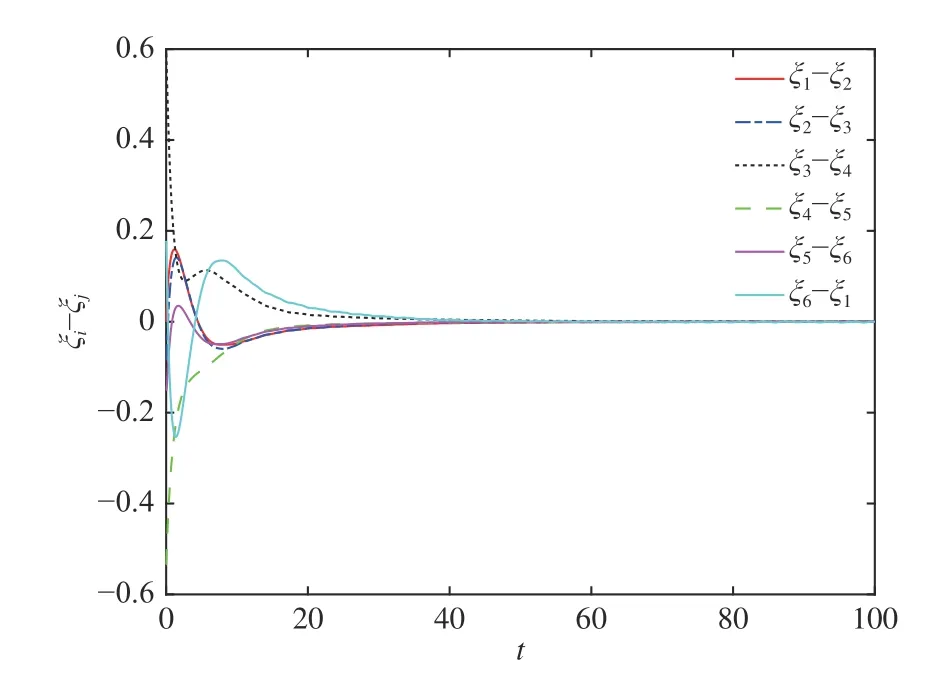
Fig. 9. The plot of

V. Conclusion

This paper develops the circular formation flight control problem for the bidirectional network into a directed case with an unknown, bounded disturbance. Based on backstepping technology, consensus and the ISS theory for the cascade system, a new fully distributed control law is constructed. As pointed in [16], it is difficult to deal with the circular formation tracking control problem under the directed network with joint connectivity. Therefore, we will devote ourselves to solving it in our next work.