傅惠民， 文歆磊

（北京航空航天大学 小样本技术研究中心， 北京 100191）

0 引言

复杂系统的可靠性评估与实时更新是当前研究的热点问题[1，2]。文献[3]严格证明了串（并）联系统可靠度（不可靠度）单侧置信下（上）限等于各子系统可靠度（不可靠度）单侧置信下（上）限的乘积，提出了串并联系统可靠度置信下限的计算方法。 本文进一步建立子系统可靠度和差积商的置信限公式， 解决了一般复杂系统可靠度的置信限计算难题。 同时，建立系统寿命和可靠度实时更新方法， 能够通过子系统可靠度置信限和当前系统试验数据的有机融合，实现系统寿命和可靠度的高精度实时更新。

1 和差积商的置信限

要解决一般系统的可靠性评估问题， 首先需建立关于和差积商置信限的四个引理。

设λL和λU分别为母体特征值λ（如母体均值、方差、百分位值、百分率、分布参数等）置信度为γ的单侧置信下限和上限，即

根据文献[4]，式（1）或式（2）可以看作λ的置 信 分布函数。

引理1 设两个母体特征值λ1≥0 和λ2≥0 的置信度为γ的单侧置信下限分别为λL1≥0 和λL2≥0，且λL1与λL2相互独立， 则它们之和λ=λ1+λ2的单侧置信下限λL=λL1+λL2的置信度γ*由下式计算

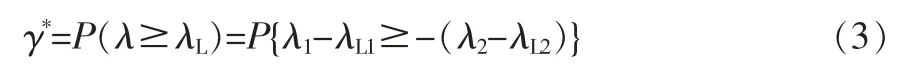
特别地，当γ≥50%时，有γ*≥γ。

若令X1=λ1-λL1，X2=-（λ2-λL2），则有γ*=P（X1≥X2），因此，γ*可由随机变量X1和X2的干涉模型计算，具体见文献[3]。 下面的3 个引理也可以同样证明。

引理2 设两个母体特征值λ1≥0 和λ2≥0 的置信度为γ的单侧置信下限和上限分别为λL1≥0 和λU2≥0，且λL1与λU2相互独立，则它们之差λ=λ1-λ2的单侧置信下限λL=λL1-λU2的置信度γ*由下式计算

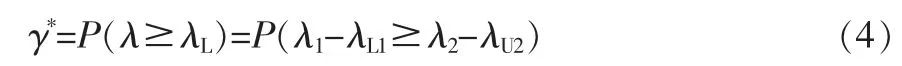
特别地，当γ≥50%时，有γ*≥γ。

引理3 设两个母体特征值λ1＞0 和λ2＞0 的置信度为γ的单侧置信下限分别为λL1＞0 和λL2＞0， 且λL1与λL2相互独立， 则它们之积λ=λ1λ2的单侧置信下限λL=λL1λL2的置信度γ*由下式计算

特别地，当γ≥50%时，有γ*≥γ。

引理4 设两个母体特征值λ1＞0 和λ2＞0 的置信度为γ的单侧置信下限和上限分别为λL1＞0 和λU2＞0，且λL1与λU2相互独立， 则它们之商λ=λ1/λ2的单侧置信下限λL=λL1/λU2的置信度γ*由下式计算

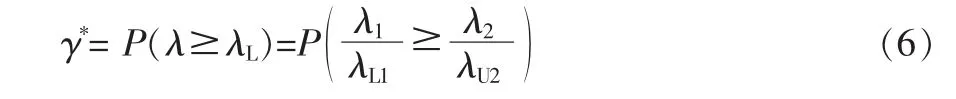
特别地，当γ≥50%时，有γ*≥γ。

对于λ1＜0 或λ2＜0 的情况，可以令λ1'=-λ1或λ2'=-λ2，上述四个引理仍然成立。 由于置信度为1-γ的单侧置信下限即为置信度为γ的单侧置信上限， 所以根据上述四个引理也可求得和差积商的单侧置信上限， 并且可以解决多个母体特征值和差积商及其组合的置信限问题。 此外，将置信度换成置信水平，上述四个引理仍然成立。

2 系统可靠性评估方法

根据上述四个引理， 可以方便地建立关于系统可靠性的四个定理。

定理1 设R1和R2分别为两个相互独立的子系统的可靠度，RL1和RL2分别是其置信度为γ的单侧置信下限，则它们之和R=R1+R2的单侧置信下限RL=RL1+RL2的置信度γ*由下式计算

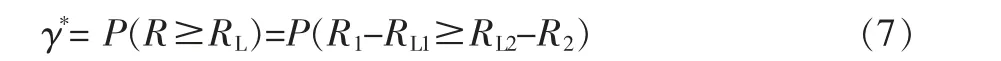
特别地，当γ≥50%时，有γ*≥γ。

根据式（7），γ*可通过下式进行数值计算

式中

实际计算时，首先按精度要求选取m（如取104，105，106等），代入式（11）计算γi，再由式（10）得到RL1，γi，然后代入式（9）计算γ～i，最后由式（8）得到置信度γ*。

定理2 设R1和R2分别为两个相互独立的子系统的可靠度，RL1和RU2分别是其置信度为γ的单侧置信下限和上限，则它们之差R=R1-R2的单侧置信下限RL=RL1-RU2的置信度γ*由下式计算

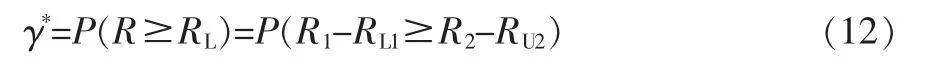
特别地，当γ≥50%时，有γ*≥γ。

根据式（12），γ*可通过式（8）求得，其中RL1，γi和γi仍由式（10）和式（11）计算，γ～i由下式给出

定理3 设R1和R2分别为两个相互独立的子系统的可靠度，RL1和RL2分别是其置信度为γ的单侧置信下限，则它们之积R=R1R2的单侧置信下限RL=RL1RL2的置信度γ*由下式计算

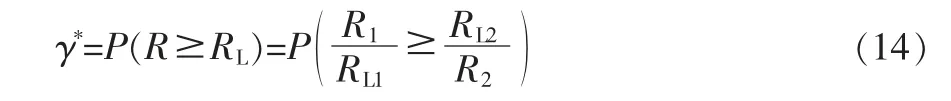
特别地，当γ≥50%时，有γ*≥γ。

根据式（14），γ*可通过式（8）求得，其中RL1，γi和γi仍由式（10）和式（11）计算，γ～i由下式给出

定理4 设R1和R2分别为两个相互独立的子系统的可靠度，RL1和RU2分别是其置信度为γ的单侧置信下限和上限， 则它们之商R=R1/R2的单侧置信下限RL=RL1/RU2的置信度γ*由下式计算

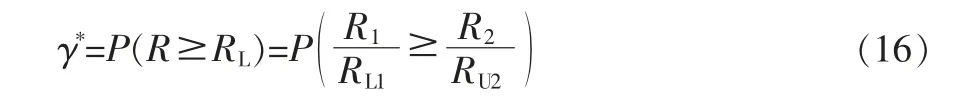
特别地，当γ≥50%时，有γ*≥γ。

根据式（16），γ*可通过式（8）求得，其中RL1，γi和γi仍由式（10）和式（11）计算，γ～i由下式给出

由于置信度为1-γ的可靠度单侧置信下限即为置信度为γ的可靠度单侧置信上限， 所以根据上述四个定理也可求得可靠度和差积商的单侧置信上限。 此外，将置信度换成置信水平，上述四个定理仍然成立。

鉴于一般系统的可靠度是各子系统可靠度的和差积商及其组合， 因此上述四个定理能够很好地解决一般系统的可靠性评估问题。

3 成败型试验可靠性更新方法

3.1 置信度更新

设产品（系统）可靠度R 的置信度为γ的单侧置信下限为RL，γ，即

式中，事件B={R≥RL，γ}，其对立事件B¯={R＜RL，γ}。

现投入n 个当前产品进行成败型试验， 共r 个产品失败，n-r 个产品成功。 此时有

式中，事件A={r 个产品失败，n-r 个产品成功}。

根据Bayes 公式可知，在事件A 发生的条件下，当前产品可靠度R 的单侧置信下限RL，γ的置信度可以更新为

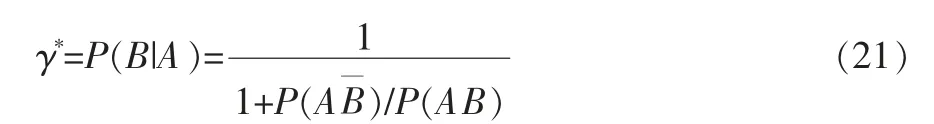
式中

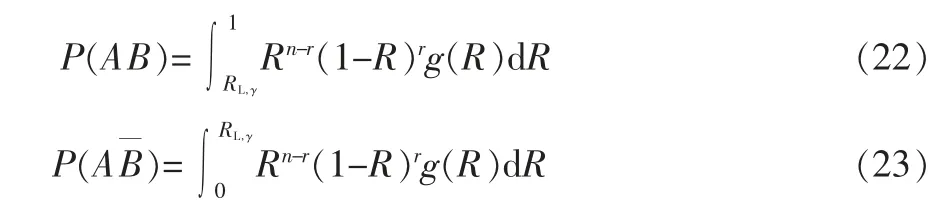
其中，g（R）为可靠度R 的置信分布[4]。 式（22）和式（23）的数值计算公式为

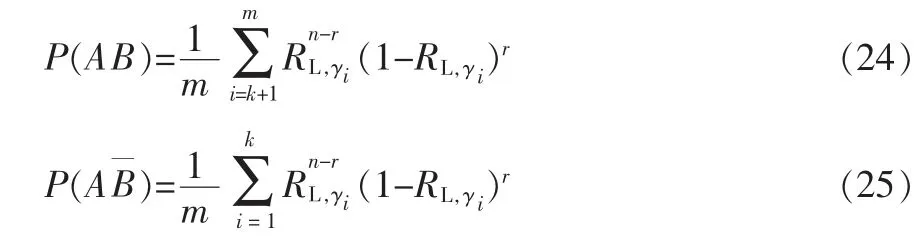
式中

m 可根据精度要求进行取值 （如取104，105，106等），并且应使mγ为整数。

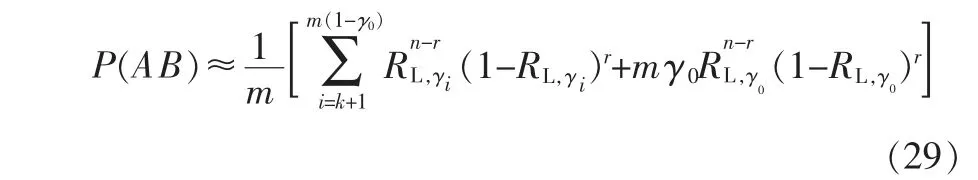
对于只能求得置信度γ≥γ0的可靠度单侧置信下限的情况，可以将P（AB）的近似值代入式（21）计算。 此时要求γ0较小，这样上式中最后一项也就相对较小，最终γ*的计算误差很小。 下面类似的近似计算误差也同理很小。另外，选取的m 也应使mγ0为整数。

3.2 可靠度更新

对于给定的置信度γ，由式（21）可以求得更新后的置信度γ*，并通过不断调整γ的取值至γ**，使得更新后的置信度γ*等于给定的置信度γ，即γ*=γ。 此时，可将原来可靠度R 的置信度为γ的单侧置信下限RL，γ更新为RL，γ**。

4 非成败型试验可靠性更新方法

同样，设产品（系统）在t0时刻可靠度R 的置信度为γ的单侧置信下限为RL，γ，即满足式（18）和式（19）。

现对n 个当前产品进行寿命试验，事件A={r 个失效数据t1，t2，…，tr，n-r 个未失效数据tr+1，tr+2，…，tn}发生。 并设当前产品寿命的概率密度函数为f（t，θ），可靠度函数为R（t，θ）。 此时有

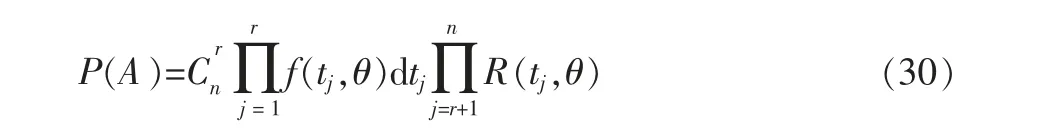
4.1 置信度更新

在事件A 发生的条件下，当前产品可靠度R 的单侧置信下限RL，γ的置信度可由下式进行更新

式中

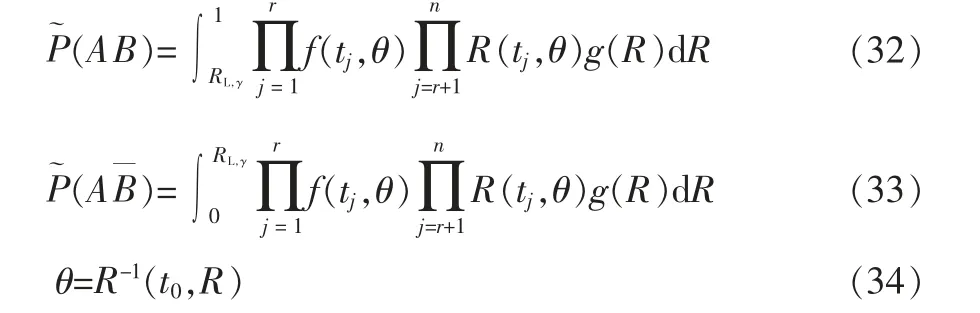
式（32）和式（33）的数值计算公式为

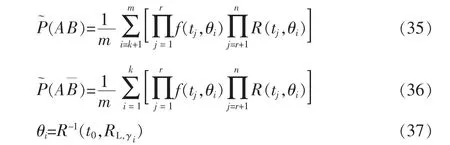
式中，RL，γi和k 仍由式（26）～式（28）给出。

同样， 对于只能得到置信度γ≥γ0的可靠度单侧置信下限的情况，可以将P～（AB）的近似值

代入式（31）计算。

特别地， 当r=0， 即试验结果均为无失效数据时，式（35）和式（36）简化为

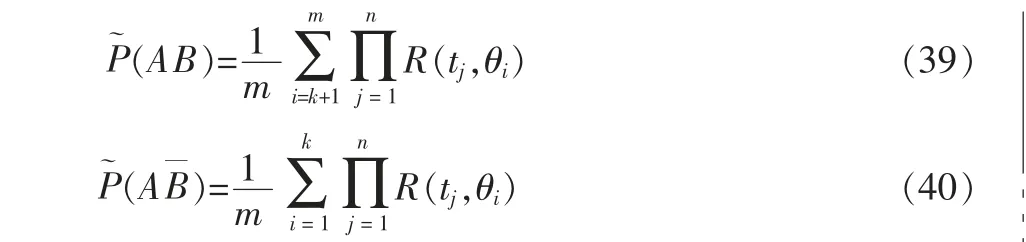
对于只能得到γ≥γ0的RL，γ的情况，P～（AB）的近似值为

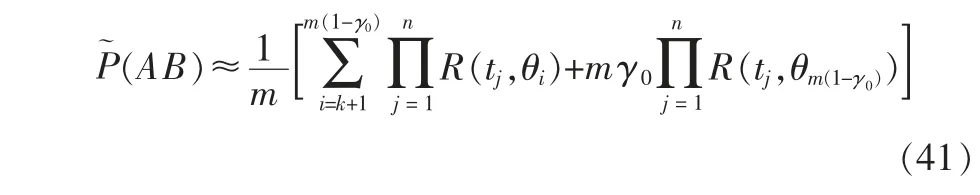
4.2 可靠度更新

可靠度的更新与3.2 节类似， 对于给定的置信度γ，可以由式（31）求得更新后的置信度γ*，并通过不断调整γ的取值至γ**，使得更新后的置信度γ*等于给定的置信度γ，即γ*=γ。 此时，可将原来可靠度R 的置信度为γ的单侧置信下限RL，γ更新为RL，γ**。

5 非成败型试验寿命更新方法

设给定可靠度R0时，置信度为γ的可靠寿命tR的单侧置信下限为tRL，γ，即

式中，事件B={tR≥tRL，γ}，其对立事件={tR＜tRL，γ}。

现投入n 个当前产品（系统）进行寿命试验，事件A发生（事件A 定义与第4 节相同），并设当前产品寿命的概率密度函数为f（t，θ），可靠度函数为R（t，θ），则P（A）仍由式（30）给出。

5.1 置信度更新

在事件A 发生的条件下，当前产品可靠寿命tR的单侧置信下限tRL，γ的置信度仍由式（31）给出，其中

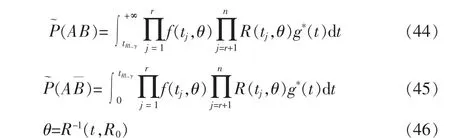
式中，g*（t）为可靠寿命tR的置信分布[4]。 同样，可通过式（35）和式（36）对式（44）和式（45）进行数值计算，此时

式中，γi和k 仍由式（27）和式（28）给出。 对于只能得到置信度γ≥γ0的可靠寿命单侧置信下限的情况，P～（AB）的近似值仍通过式（38）求得。 当试验结果均为无失效数据时，仍由式（39）～式（41）进行计算，此时θi由式（47）给出。

5.2 可靠寿命更新

对于给定的置信度γ，可以先通过5.1 节方法求得更新后的置信度γ*，然后不断调整γ的取值至γ**，使得更新后的置信度γ*等于给定的置信度γ，即γ*=γ。 此时，可将原来可靠寿命tR的置信度为γ的单侧置信下限tRL，γ更新为tRL，γ**。

6 Weibull 分布可靠性和寿命更新方法

设当前产品寿命t 服从Weibull 分布，其概率密度函数和可靠度函数由下式给出

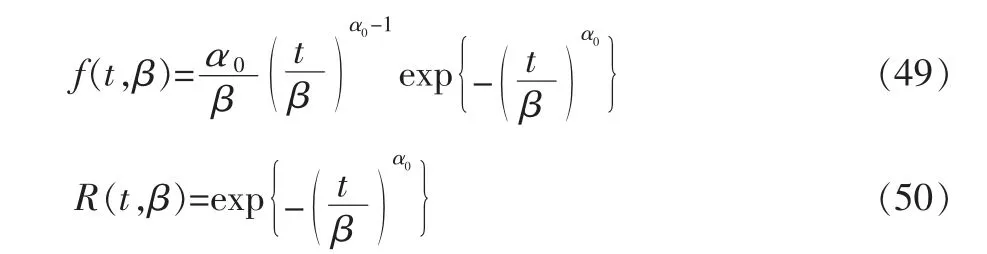
式中，α0为形状参数，β 为尺度参数。α0为一已知常数（或为其已知下限），它可以通过以往试验数据获得（例如，对于铝合金结构，α0=4；钛合金结构，α0=3；钢结构，α0=2.2）[5]。

设已知在t0时刻可靠度R 的置信水平为γ的单侧置信下限为RL，γ，或者在给定可靠度R0处可靠寿命tR的置信水平为γ的单侧置信下限为tRL，γ。 现投入n 个产品进行寿命试验，在事件A 发生的条件下，则可采用第4 节和第5 节方法，分别对其可靠度和寿命进行更新，其中

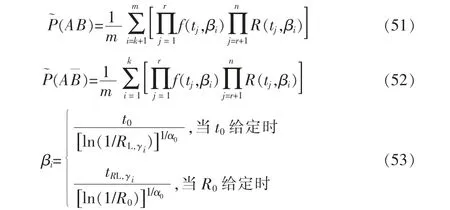
7 对数正态分布可靠性和寿命更新方法

设当前产品的对数寿命x=lgt 服从正态分布，其概率密度函数和可靠度函数由下式给出

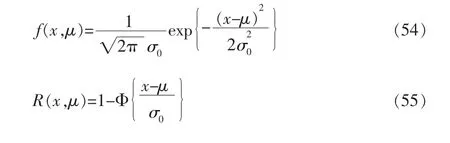
式中，Φ（·）为标准正态分布函数，μ 为对数寿命均值，标准差σ0为一已知常数（或为其已知上限）。

设已知在x0=lgt0时刻可靠度R 的置信水平为γ的单侧置信下限为RL，γ，或者在给定可靠度R0处对数可靠寿命xR的置信水平为γ的单侧置信下限为xRL，γ。 现投入n个产品进行寿命试验，在事件A 发生的条件下，同样可采用第4 节和第5 节方法， 分别对其可靠度和寿命进行更新，其中

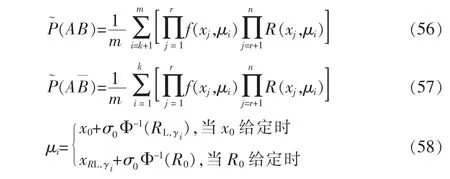
8 算例

8.1 桥式系统可靠度置信下限评估

设某桥式系统由5 个完全相同且相互独立的子系统构成，各子系统可靠度相同（即R1=R2=R3=R4=R5），则该桥式系统的可靠度R 为

根据定理1～定理3 可知， 该桥式系统置信水平为γ的可靠度单侧置信下限RL由下式给出

式中，RL1和RU1分别为子系统可靠度R1的置信水平为γ的单侧置信下限和上限。

8.2 单一系统可靠度置信下限更新验证

现对100 个产品开展成败型试验， 共有5 个产品失败，95 个产品成功， 则其置信度γ=0.9 的可靠度单侧置信下限RL，γ=0.909。接着，又投入20 个相同的产品进行成败型试验， 结果全部成功， 采用第3 节方法对置信下限RL，γ=0.909 进行更新，可将其提高到0.924。

此外，由于两次成败型试验数据都属于同一母体，可将它们作为一个整体进行统计分析， 求得置信度γ=0.9的可靠度单侧置信下限为0.924。

从上述结果可以看到，对于单一系统来说，本文方法与传统方法得到的结果完全一致， 这不仅验证了本文方法的正确性， 而且说明在更新过程中没有造成任何信息丢失。对于多个子系统构成的复杂系统，传统方法已不适用，而本文方法仍能很好地进行更新。

8.3 工程算例

某航天器由两个完全相同的零部件串联组成， 首先对10 个零部件进行寿命试验， 每个试件均在106循环处中止，未发生失效。 已知零部件的寿命服从形状参数α0＝3 的两参数Weibull 分布，求得该航天器置信水平γ=0.9、可靠度R=0.999 的寿命单侧置信下限为[3，5]

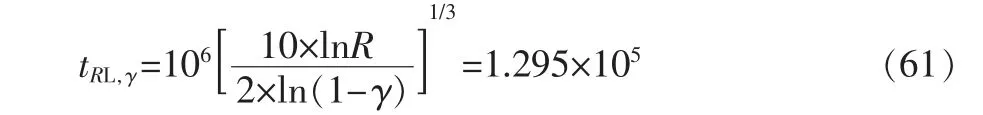
然后又投入一台该航天器整机进行寿命试验， 截止到2×106循环仍未失效。 采用第5 节方法对式（61）的寿命预测结果进行更新，此时γ0＝0.005[5]，求得γ**=0.588，从而将可靠寿命单侧置信下限由tRL，γ＝1.295×105提高至

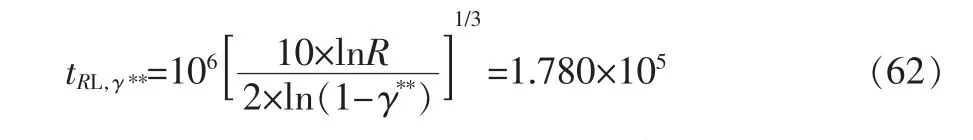
从上述计算结果可以看到， 本文建立的更新方法能够将零部件和整机的试验结果有机融合， 把整机的可靠寿命单侧置信下限提高了37.5%。

9 结论

基于置信分布，提出和差积商的置信限理论，给出子系统可靠度和差积商的置信限公式， 进而建立一种系统可靠性评估方法，解决了一般系统的可靠性评估难题。

提出一种系统可靠度和寿命更新方法， 能够利用当前系统的试验数据， 对系统原来的可靠度和寿命评估结果进行实时更新。 在此基础上， 详细讨论了常用的Weibull 分布和对数正态分布的寿命和可靠度更新问题。

对于一个零部件有多种失效模式和多个危险部位的情况，若它们彼此之间相互独立，则可以将它们看作该零部件的广义子系统， 也能用本文方法进行可靠性评估和更新。

大量工程算例和Monte Carlo 模拟验证表明，本文方法能够有效提高可靠性评估和寿命预测精度， 且计算简单，便于工程应用。