随机利率下带注资的对偶模型最优分红问题
2020-04-17彭小飞
邓 丽, 郑 华*, 彭小飞
(1. 韶关学院数学与统计学院, 韶关 512005; 2. 华南师范大学数学科学学院, 广州 510631)
随着公司股份制改革,为了保证公司现金流的充足和运营安全,公司在发行股票筹集资金时需考虑回馈作为投资者的股东,即分红. 分红问题中,讨论得较多的有经典风险模型和风险对偶模型[1-6],其中风险对偶模型可描述为[1]:
U(t)=u-ct+S(t) (t+,u),
(1)
其中,U(0)=u表示公司的初始资金,正整数c表示在单位时间(t-1,t]内的支出,S(t)表示直到t时刻的总收益.
风险对偶模型中研究得较多的分红策略有:Barrier策略[1]和Threshold策略[2],例如:运用Laplace变换方法讨论了复合Poisson对偶模型的最优分红Barrier的确定方法[1];利用2个Integro积分方程和Laplace变换给出了最优分红Threshold的计算方法[2]. 显然,在最优分红问题中,既提高股东收益又降低公司风险的方案应当同时考虑分红与再注资[7-13],例如:在离散经典风险模型中证明了最优值函数是一个Hamilton-Jacobi-Bellman(HJB)方程的唯一解,指出再注资后最优分红策略是Barrier策略[7];在对偶模型中证明了带注资的最优分红策略为Barrier策略[8];讨论了带比例和固定交易费的再注资的最优分红问题,并通过数值实例说明分红边界随交易费比例的增加而上升[9];在复合二项风险模型中证明了最优值函数是一个HJB方程的唯一解,并验证了最优控制策略是双Barrier策略[10]. 为了更贴合实际,考虑分红贴现利率的变化具有随机性[14-15],例如:在随机利率下讨论了离散风险模型中具有延迟索赔的最优分红问题,得到了最优策略的一个高效算法[14].
本文在红利有界的条件下,研究复合二项对偶模型中带比例交易费再注资且分红贴现利率随机变化的最优分红问题;运用压缩映射不动点原理证明了该最优分红问题的最优值函数是一个离散HJB方程的唯一解,得到了最优分红策略和最优值函数的计算方法;为了能在实际运用中计算最优红利值,根据分红策略的一些性质得到了该最优值函数的可无限逼近的上界和下界;最后给出数值实例来验证本文所给的最优分红策略的有效性.
1 预备知识
文中用到的相关记号、符号如下:
(ii)c,C,m,x+;i,j=1,2,…,m.
(iv)a1∨a2=max{a1,a2},a1∧a2=min{a1,a2}.
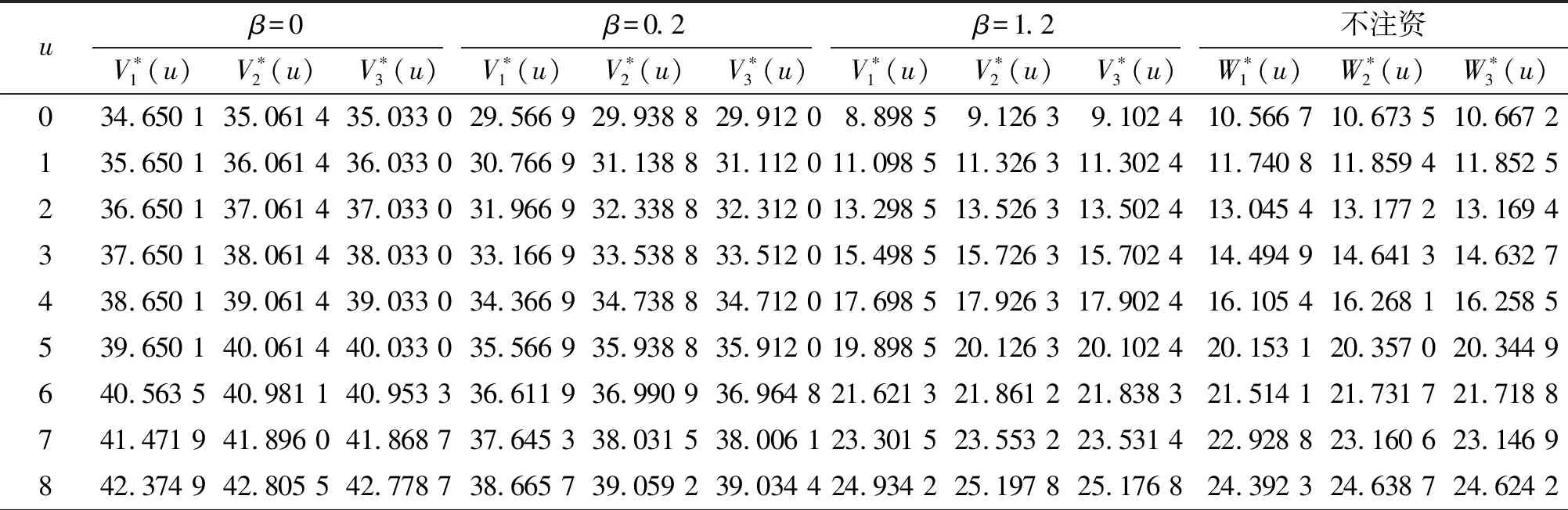
假设任意单位时间(t-1,t](t+)内至多有一次收入,在t的前一瞬时结算. 用εt=1表示有一次收入,收入量为Xt+;εt=0表示无收入. 序列{Xt}和{εt}分别为独立同分布的随机变量,其中{εt}具有概率Pr(εt=1)=p(0 再假设(t-1,t]时间段的利率{Rt,t+}是有限状态空间{r1,r2,…,rm}的关于t可测的齐次 Markov 链,一步转移概率阵为其中pij=Pr(Rt+1=rj|Rt=ri). 令vi(0 在模型(1)中引入分红策略. 假设在0时刻不考虑分红,分别用dt和zt表示t(t)时刻的分红和再注资,记d0=0. 在任何时刻t的分红策略满足以下4个条件称为可行的策略:(1)dt取整数且有上界C;(2)dt和zt关于t可测;(3)盈余u不大于c时不分红,并由股东注入相应的资金c-u(存在交易费),使盈余能够快速恢复到c;(4)盈余u不小于c时不注资,分红由超出c的部分承担. 由于模型(1)具有Markov性质,所以只需讨论依赖于各时刻盈余的可行策略,这类策略是关于盈余的函数,组成的集合用Λ表示. 为方便讨论,用φi(u)表示盈余为u、利率状态为ri时的分红量,则任意时刻t(t+)的利率Rt=rj时的分红量为φj(U(t-1)-c+Xtεt). 故初始利率为R0=ri的累积分红折现均值函数(以下简称值函数)[7]为 (2) 优化目标是找到最优值函数 对任意的φi(u)Λ,根据全期望公式[17],带比例交易费再注资的值函数Vi(u)满足: (3) 其中β(β≥0)为交易费的比例(常量). 定理1对任意的φi(u)Λ,最优值函数满足如下 HJB 方程: (4) 证明对式(3)取最优值得: (5) 显然式(5)与式(4)等价. 证毕. 定义1[16]记H表示所有m维有界实序列组成的集合. 对H中任意两点X=(Xi(u))和Y=(Yi(u))(u,i=1,2,…,m),称 为X、Y的距离. 显然H=(H,d)是完备度量空间,且任意的V=(Vi(u))H. 对任意的V=(Vi(u))H(i={1,2,…,m}),定义 记T=(T1,T2,…,Tm),其中Ti(i=1,2,…,m)为H上的m个算子,满足: bVj(u-c+x)]f(x) (u≥c), (6) 或 TV=(T1V,T2V,…,TmV), (7) 则式(4)中u≥c的部分等价于 TiV=Vi, (8) 或 TV=V. (9) 定理2方程(9)有且仅有唯一解. 证明假设对任意Xi(u),Yi(u)H,i={1,2,…,m},及给定的u≥c,Xi(u-bXi(u))+bXi(u)≥Yi(u-bYi(u))+bYi(u),因为Yi(u-bYi(u))+bYi(u)≥Yi(u-bXi(u))+bXi(u),所以 故对任意的u≥c,有 d(TX,TY)≤vd(X,Y). 在0 结论1对任意u,i={1,2,…,m},方程(4)有且仅有唯一解,且该唯一解为最优值函数 定理3对任意的φi(u)Λ,u,i={1,2,…,m},Vi(u)取最优值时当且仅当 (10) 证明(1) 必要性. 由模型的假设知,当0≤u≤c时,φi(u)=0. 对任意的i={1,2,…,m},若Vi(u)是最优的值函数,则Vi(u)满足式(3)、(4). 比较式(3)与式(4),当u>c时,有 因此式(10)成立. (2)充分性. 因方程(4)的解存在且唯一,故充分性成立. 证毕. (11) 由不动点原理及式(8)、(11)得 (12) 当时间区间(t-1,t]内可能的收入不是有界的随机变量时,递归式(11)中的函数序列存在无穷项之和,不便于数值计算. 在C<的情形下,对任意的n1+,考虑如下2个方程: (13) (14) 定理4对任意的u,i={1,2,…,m},有 (15). 因此, 推论1对任意的0 (16) 证明由式(13)、(14),当0≤u 当u≥c时,由定理2的证明过程,有 则式(16)成立. 证毕. 综上可得最优红利值的算法: 第1步,精度控制. 给定一个精度要求,根据式(12)得到迭代步数n及式(16)中n1的值. (17) 例1假设p=0.7,c=C=5,收入量服从均值为μ=10的几何分布,概率函数为: 再假设利率为:r1=0.05,r2=0.04,r3=0.03,转移概率矩阵为: 表1 最优分红策略 表2 最优值函数 续表2 本文在复合二项对偶模型中讨论了带比例交易费再注资且分红贴现利率随机变化的最优分红问题,运用压缩映射不动点原理证明了该最优分红问题的最优值函数是一个离散的HJB方程的唯一解,得到了最优分红策略和最优值函数的优化算法. 数值实例结果表明:当交易费比例控制在一定范围内时,相应的最优红利值大于未注资的最优红利值,说明了文中最优分红策略的有效性. 在今后的工作中,可进一步研究最优分红策略的Threshold性质,也可尝试在红利无限制的条件下讨论最优分红问题.
2 最优分红策略和最优值函数

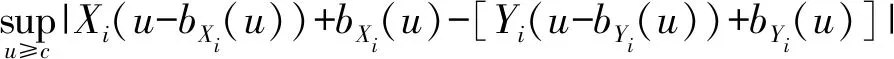


3 最优红利值的算法
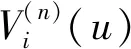
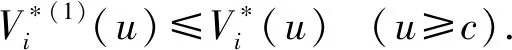

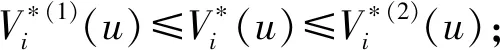

4 数值模拟

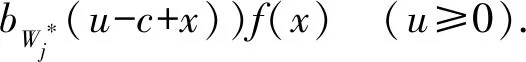


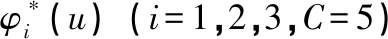

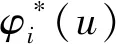
5 小结
