江苏省苏州市阳山实验初级中学校 (215151) 尹国益

本文系苏州市教育科学“十三五”规划2019年度课题“发展初中生数学建模素养的教学实践研究”(课题编号：192010343)的阶段性成果.

一、选题背景

笔者作为初三的一线教师，一直着力研究如何提高学生中考的复习效率，思考如何从无限的题海中提炼出有限的题型，找到解题的策略与方法，从而减轻学生复习压力，培养学生分析问题、解决问题的能力，提高他们的综合素养.有一次，本人遇到了所在地区的一次期末考试题第28题，在阅卷和试卷讲评中，发现学生存在以下问题：试题难度较高，很多学生不知道如何处理线段和的最值问题，找不到解题切入点；系数不为1的线段不会转化，不能抓住一些细节，找不到解题的关键点；计算能力比较薄弱，很难抓住解题的得分点,等等诸如此类的很多.探究根源,其实质还是学生未能抓住题目的本质，未能把掌握试题的结构特征，未能找到与之相关的基本知识点.现将这类题型提炼出来，探索其解题思路，总结解决策略方法.

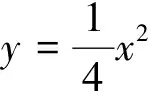
(1)求这条直线的函数表达式;

(2)在x轴上是否存在点C，使得ΔABC是直角三角形?若存在，求出点C的坐标，若不存在，请说明理由;

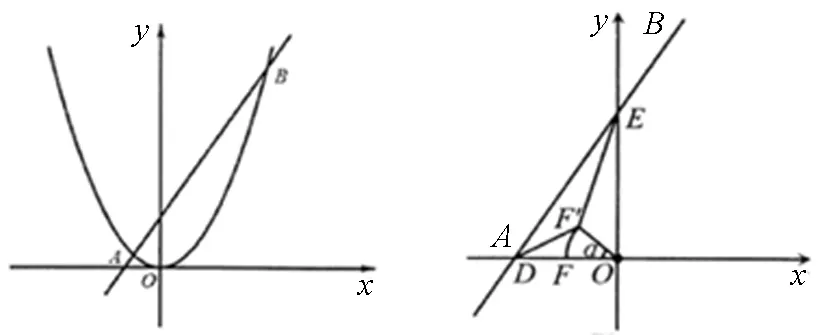
图1 图2

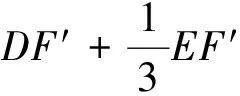
分析思考：第(1)问是辅助性试题，第二问是存在性问题都比较容易解决.笔者重点研究问题(3)的解决策略.问题(3)是线段和的最值问题，但又不是单纯线段的和，(并不是所有线段的系数为1)简称″kAB+CD″型的最值问题，这类题型是中考常考查的题型，题型难度系数较高，题目阅读量也比较大，里面牵涉的知识点也比较多.学生往往无从下手.如何处理这类问题?需要我们教师在平时教学中，一定要多带领学生读题审题，抓住试题的关键信息，把握题型特征，进行适当转化，提炼出这类题型的解决策略.[2]这个过程不但可以探究这类题型的解法，更渗透了一些数学思想，从而进一步培养学生分析问题、解决问题的能力，提高他们的数学素养.

二、追根溯源

线段最值问题是平面几何中比较经典的问题，要让学生明白：从几何角度处理线段最值问题，在初中阶段有两个基本知识点：一是两点之间线段最短；二是直线外一点与直线上所有点的连线中，垂线段最短.两个线段和的最值问题就可以优先利用上述知识点解决.

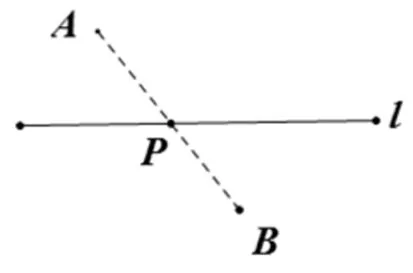
图3

模型1(如图3)在线段l上找点P，使得PA+PB最小.即当A、B、P三点共线时最小.(将军饮马问题)

模型2(如图4)平面内一定点A，在线段m上找点P，过点P作PB⊥l于点B,使得PA+PB最小，即当A、B、P三点共线时最小.(胡不归问题)

图4

注：模型1是经典的将军饮马问题，两个定点一动点，若A、B在l同侧，还要利用对称性，将同侧转化为异侧，再借助两点之间线段最短.模型2是胡不归问题,虽然有两个动点一个定点，但依据题目本身的特征，PB始终与l垂直，自然要利用垂线段最短原理.上述基本模型都是从两个最短问题提炼出来的，共性都是求两个有公共端点的线段和的最值问题，所求的都是“单纯”两个线段的和，(即每个线段系数都为1)，但遇到系数为k(k≠1)的线段，我们该如何转化?这就是我们研究的主要内容.

三、解法探究

图5

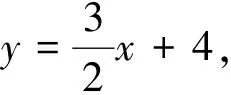
注：本题主要抓住对数据的处理与整合，构造了一个“反A字型”相似.将系数不为1的线段进行转化，转化成两个有公共端点的单独线段(系数为1)和的最值问题，再利用基本模型解决.在转化时，一定要透彻地分析已知量，辨析题型的结构，把握其特征，找到转化的路径.但有时转化不一定要用到相似形，还有一些其他方法，故找了一些对应的题型进行深度探究，提炼出解题方法与策略.

变式训练：如何求3DF′+EF′的最小值？

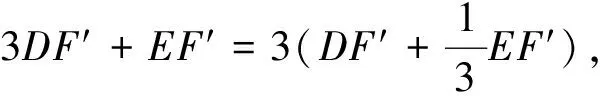
四、方法提炼

1.构造相似三角形

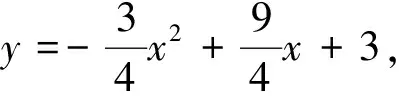
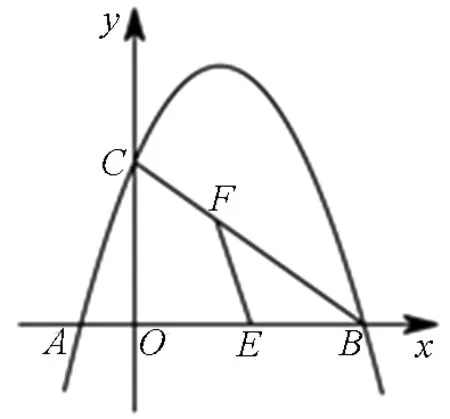
图6

图7

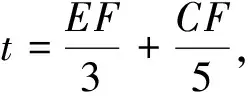
2.构造特殊角的三角函数值

图8

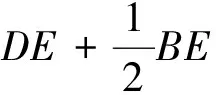
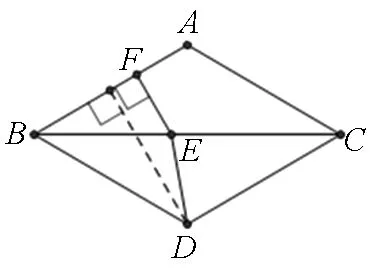
图9

3.构造函数关系式

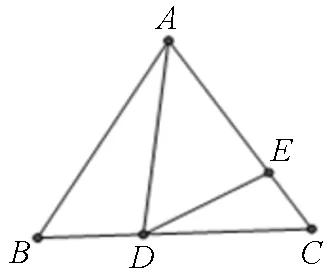
图10

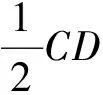
五、解题反思

本文主要探究了“kAB+CD”型的最值问题，虽然问题的背景在变，但解题的思想方法不变，重点是把握题型结构特征，将系数k进行转化，通过构造相似形、特殊角的三角函数值，函数关系式等方法进行处理.因此，在平时解题教学中，教师一定要引导学生学会审题，结合已知条件辨析题型的特征，从宏观上把握已知量和未知量内在的联系，从而更容易探究解题方法.这正如波利亚曾说过，假如你想要从解题中得到最大的收获，你就应当在所做的题目中去找出它的特征，那些特征在你以后求解其他问题时，能引起指引的作用.这要求我们教师在解题教学时要重过程、讲方法，最好能提炼出一类题型的通解.

解题教学不光要教“解法”，更要教“想法”，因此在解题过程中，教师要回归基础，从学生掌握的基本图形，基本技能出发，让学生不断地进行知识的迁移与建构，用他们已有的知识去解决新的问题，从而扩展他们的知识体系.在学生新知的建构过程中，教师要把握学生的思维方式，注重启发学生的创造性思维，不断地渗透题中所蕴含的数学思想,如转化思想、模型思想、数形结合思想等.只有这样，才能真正提高学生的解题能力和策略水平，才能达到“会一道”到“通一类”的突破，从而进一步提升学生的数学素养.