江苏省苏州市吴江经济技术开发区实验初级中学 (215000) 赵 渊

国际数学奥林匹克(IMO)已成功举办了60届.通过研究，笔者发现了一个极为有趣的命题现象：一道IMO平面几何题问世后，经过岁月的洗礼与沉淀成为经典习题，然后经过奥赛命题专家对其面貌、内涵进行合理改造，再一次变成新的IMO平面几何题.下面列举三例，让我们来感受一下这种推陈出新的命题方法.

案例1ΔABC是等腰三角形，AB=AC，O是BC的中点，M是直线AO上的点且MC⊥AC，D是线段BC上不同于B、C的任意一点，E、F分别在直线AB、AC上使得E、D、F不同并共线.求证：MD⊥EF当且仅当DE=DF.

图1

如图1，易知DE=DFBE=CF.

这是1994年7月在香港举行的第35届IMO的第2道赛题，让我们来看看19年后它是如何演化为另一道IMO试题的.

图2

去掉图1中的三线AM、MC、MD，同时将图1中的等腰ΔABC变为等腰直角三角形(见图2)：

连结AD，显然有AD=DE=DF，将ΔFCD割下后依顶点次序放到ΔAPQ所在位置(其中点P在ΔABC的外接圆上)，注意到∠FCD=∠APQ，即知P、Q、B三点共线．

将ΔDBE割下后依顶点次序放到ΔSPA所在位置，再注意到∠DBE=∠SPA，即知P、S、C三点共线．

注意到ΔFCD≌ΔAPQ，ΔDBE≌ΔSPA，知∠PQA=∠CDF=∠EDB=∠ASP，从而知∠AQB=∠ASC，结合∠ABQ=∠ABP=∠ACP=∠ACS，AB=AC，有ΔABQ≌ΔACS，故BQ=CS．

再注意到PQ=CD，PS=BD，即知点D、P、Q是ΔPBC的三边BC、PB、PC与相应的旁切圆的切点．

连结QS，注意到AQ=DF=AD=DE=AS，即知点A是ΔDQS的外接圆圆心．于是，2013年7月在哥伦比亚的圣玛尔塔市举行的第54届国际数学奥林匹克(IMO)的第3道赛题生成：

新赛题D、Q、S分别是ΔPBC的旁切圆在其边BC、PB、PC上的切点，证明：若ΔDQS的外心在ΔPBC的外接圆上，则ΔPBC是直角三角形.

案例2 已知ΔABC为锐角三角形，AB≠AC；以BC为直径的圆分别交边AB和AC于点N和M．记BC的中点为O．∠BAC和∠MON的角平分线交于R．求证：ΔBNR的外接圆和ΔCMR的外接圆有一个公共点在BC边上．

如图3，连结MN、BM、CN，则∠BMC=∠CNB=90°．故BM与CN的交点H是ΔABC的垂心，从而A、M、H、N四点共圆(⊙O3)．

图3

连结RM、RN，则∠ARN=∠AMN=∠ABC，∠ARM=∠ANM=∠ACB，即知B、N、R、W四点共圆(⊙O1)，C、M、R、W四点共圆(⊙O2)．

综上，ΔBNR的外接圆(⊙O1)和ΔCMR的外接圆(⊙O2)有一个公共点(W)在BC边上．

这是2004年7月在希腊首都雅典举行的第45届IMO的第1道赛题.下面，我们来看10年后它是如何演化为另一道IMO试题的.

如图3，设直线RH与⊙O1交于点X，与⊙O2交于点Y，连结WX、WY，即知WX是⊙O1的直径，WY是⊙O2的直径，从而知X、R、H、Y四点共线.

于是，2013年7月在哥伦比亚的圣玛尔塔市举行的第54届IMO的第4道赛题生成：

新赛题设ΔABC是一个锐角三角形，其垂心为H，设W是边BC上一点，与顶点B，C均不重合．M和N分别是过顶点B和C的高的垂足．记ΔBWN的外接圆为⊙O1，设X是⊙O1上一点，且WX是⊙O1的直径．类似地，记ΔCWM的外接圆为⊙O2，设Y是⊙O2上一点，且WY是⊙O2的直径．证明：点X、Y和H共线．

案例3 设P是ΔABC内一点，∠APB-∠ACB=∠APC-∠ABC．又设D，E分别是ΔAPB及ΔAPC的内心．证明：AP、BD和CE交于一点．

图4

这是1996年7月在印度孟买举行的第37届IMO的第2道赛题，下面，让我们来看看若干年后它是如何演化为另两道IMO试题的.

显然，在案例3与图4的讨论中没有用到“P是ΔABC内一点”这一条件，故该条件是多余的，或者说该条件可修改为“P是ΔABC的∠A内一点”，因此案例3的讨论也适用于图5.

如图5，过点P作PX⊥BC于点X，PY⊥AB于点Y，PZ⊥AC于点Z，则P、X、Y、B四点共圆且该圆的直径为PB，P、X、C、Z四点共圆且该圆的直径为

图5

PC，由正弦定理得XY=PBsin∠ABC，XZ=

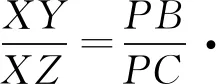
显然，在图5中，当ε=∠APB-∠ACB=∠APC-∠ABC无限趋近于0，即四边形ABPC内接于圆时，仍然有XY=XZ.

于是，2003年7月在日本首都东京举行的第44届IMO的第4道赛题生成：

新赛题1 设ABPC是一个圆内接四边形．从点P向直线AB、BC、AC和引垂线，其垂足分别为X、Y和Z．证明：XY=XZ的充分必要条件是∠BAC的平分线、∠BPC的平分线和直线BC相交于一点．

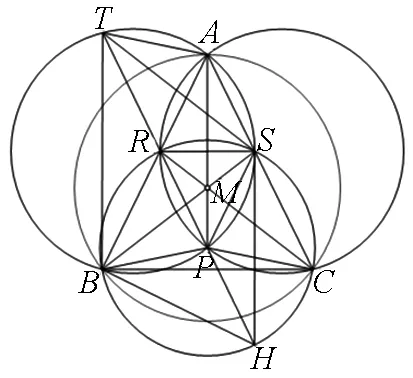
图6

如图6，延长BM交AC于点S，延长CM交AB于点R，则∠ABS=∠SBP=∠ACR=∠RCP=∠BAP=∠CAP=θ，故A、B、P、S四点共圆(⊙O1)，A、C、P、R四点共圆(⊙O2)，B、C、S、R四点共圆(⊙O3)，连结PR、PS，则∠PRB=∠ACP=∠ABP=∠PSC=2θ，故PR=PB=PC=PS，于是点P是⊙O3的圆心.

延长PR交⊙O1于点T，延长RP交⊙O3于点H，连结TA、TS、TB、HB、HS，则RH是⊙O3的直径，故∠RBH=90°.

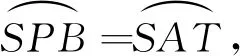
去掉⊙O1、⊙O2、⊙O3、线段RS，即可生成2016年7月在中国香港举行的第57届IMO的第1道赛题：

新赛题2 在ΔBHR中，∠B为直角．在直线RH上取点T，使得RT=RB，且R在点T和H之间；取点S，使得ST=SH，且TH为∠STB的平分线；取点A，使得AT=AS，且TS为∠ATH的平分线．设P为线段RH的中点，取点C，使得四边形ATPC为平行四边形，AC∥TH，PC∥TA．证明：直线BS、RC、PA三线共点．