陈小霞

(重庆市大足区教师进修学校 重庆 402360）

伟大科学家爱因斯坦曾说“兴趣是最好的老师，它可以激发人的创造热情、好奇心和求知欲。”在中国古代的历法中，“十天干”甲、乙、丙、丁、戊、己、庚、辛、壬、癸；“十二地支”子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥，天干地支排列组合从而衍生出一轮甲子60年。这样古老的纪年法一直沿用至今，她在闪耀华夏祖先智慧光芒的同时，更带给大家对生活、学习和工作的新思考。我们的祖先发明干支纪年法主要是为解决当时生产生活对时间长度记录的需要，是本着具体的解决问题而来的，自然就洞开了思维，也激发了探索的动力。由此可见，当我们将学习的初衷内化为奔着解决问题而来，那学习的效果一定会向着提升能力而去。为此，笔者以高中数学为例，通过排列组合案例解析，和大家一起感受数学解决实际问题的魅力。

一、排列组合思想在高中数学中的两个重要理论支撑

分类计数原理：如果独立完成一件事情有n种不同的途径，并且第一种途径有种m1不同的方法，第二种途径有m2种不同的方法……第n种途径有mn种不同的方法；那么完成该事件总共有N=m1+m2+…+mn种不同的方法。

分步计数原理：完成一件事情有n个不同的步骤：第一步有m1种不同的方法，第二步有m2种不同的方法……第n步有mn种不同的方法；那么完成该事件总共有N=m1×m2×…×mn种不同的方法。

从上述两个原理中容易发现：组合思想是分类计数原理的应用，排列思想是分步计数原理的应用。但在实际生活中，两者往往又是密不可分的，下面以具体事例说明。

二、实际生活中的排列组合案例

（一）案例一：名额分配问题

现有10台相同的电脑，配送到6个不同的工作部门，要求：每个部门至少分配一台。则可能有多少种不同的配送方法？

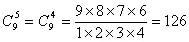
渗透核心素养：数学抽象、数学建模、数学运算。

（二）案例二：工作安排问题

某公司安排4名员工周六和周末分上下午4个时段值班，员工甲不值上午，员工乙不值周六，则不同的值班安排有多少种？

分析：值班的时段不同，值班的员工也不同，这是一个与顺序相关的，所以是排列问题。

1.法一：对立面求解

由于此处的限制元素有两个，且两限制元素有共同的限制时段即周六的上午，故可以用对立面运算。总情况（不考虑限制条件通排）有A44=4×3×2×1=24种，对立面有甲值班上午和乙值班周六（注意：甲值班周六的上午和乙值班周六上午时，两个限制条件重合，故运算时应该减去）即C21·A33+C21·A33-A33=18种。因此，满足条件的安排有N=24-18=6种。

2.法二：正面分类求解（按甲的限制条件分类）

图1

第1类（图1）：若甲排周六下午，则乙可以在周日上、下午任选（有2种可能），而剩下的2人则在剩下的2个位置任选（有A22种）故由分步计数原理得N1=2A22=4种。

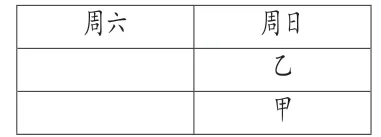
图2

第2类（如图2）：若甲排周日下午，则乙只能排周日上午，同样的，其余2人在在剩下的2个位置中任选（有A22种）即N2=A22=2种。

综上：由分类计数原理得N=N1+N2=4+2=6种。

3.法三：正面分类求解（按乙的限制条件分类）

第1类：若乙排周日上午（图3）

图3

N1=2A22=4种。

第2类：若乙排周日下午（图4）

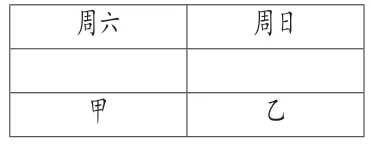
图4

N2=A22=2种。

同理：由分类计数原理得N=N1+N2=4+2=6种。

渗透核心素养：数学抽象、逻辑推理、数学建模、数据分析。

（三）案例三：列队问题（排数问题）

1.类型1：相邻元素捆绑（注意捆绑元素自身的顺序）

例如：6人列队，其中甲和乙必须相邻，则不同的排法有多少种？

分析：第1步，先将甲乙捆绑一体，考虑彼此之间的左右顺序有2种情况；第2步将甲乙看成一个整体连同剩下的5人看成6个新的整体有A66种。因此2A66种

渗透核心素养：逻辑推理；数学建模；直观想象；数学运算

2.类型2：不相邻元素插空（空格的位置和个数）

例如：6人列队，其中甲和乙不相邻，则不同的排法有多少种不同的排法？

分析：第1步，先将除甲乙以外的4人排成一列，有A44种不同的排法；第2步，在已排好位置的4人中有3个位置，以及在两端的2个位置，共5个位置中任选2位置排入甲和乙，有A52种不同的排法；最后，由分步计数原理知N=A44·A52种。

渗透核心素养：数学抽象；逻辑推理；直观想象；数学运算

3.类型3：定序均分问题

例如：6人列队，要求甲只能站在乙的右边，则有多少种不同的排法？种情况，故相当于在不考虑甲和乙的限制下通排后，再平均分成

分析：甲和乙有A22种排法，而甲站在乙的右端只是其中的一A22份，而甲站在乙的右端只站其中的一份。所以N=A66/A22种。一般的，在排列中要求特殊元素顺序一定时，都会用所有元素的全排列除以定序元素的全排列。又如：6人排成一列，要求甲乙丙三人从左到右按照身高从高到低的顺序排成一列，则N=A66/A33种。

渗透核心素养：数学抽象；逻辑推理；数学建模；直观想象；数学运算

（四）案例四：均分与部分均分分组问题

例如：将A、B、C、D个人平均分成2组，有多少种不同的分法？

分析：此处只需要将两个人分成一组，而不必管组内人员的分工，所以它是一个无序问题。第一步，从4人中任选两人作为第一组（或第二组）的元素；第二步，将第一步选后剩下的元素作为另一组。第三步，此处只管将4人分2组，而不必区分谁是第一组，谁是第二组，所以应该除以平均分得的组数的全排列。综上知：N=C42·C22/A22=3种。另解(枚举)AB+CD；AC+BD；AD+BC同理，将6人平均分成3组共有分法数为N=C62·C42·C22/A53=15种。枚举为AB+(CDEF)有(AB+CD+EF；AB+CE+DF；AB+CF+DE)3种；同理，AC+(BDEF)，AD+(BCEF)，AE+(BCDF)，AF+(B CDE)各有3种，故由分类计数原理知总数为15种。一般地，将不同的元素完全平均（或者部分平均）分成n组，第一步按组顺序选择，第二步除以平均分得的组数的全排列。如：将5本不同的故事书分给3个小朋友，其中2人得2本，另1人得1本。可以先分成3个组，其中由于有2个组是平均分，故分组N1=C52·C32·C11/A53=15种；然后再将分好的3组排给3个小朋友为A33=6种，由分步计数原理有N=15×6=90种。

渗透核心素养：数学抽象；逻辑推理；数学运算

（五）案例五：染色问题

例如：用5色染4区，要求相邻的区域颜色不能相同。

分析：第1类：0组颜色相同（用4色）；N1=A54=5×4×3×2×1=120种。

图5

第2类：只有一组颜色相同（用3色）（有两个区域颜色相同AD或者BC）N2=2A53=2×5×4×3=120

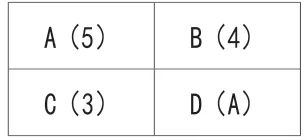
图6.1

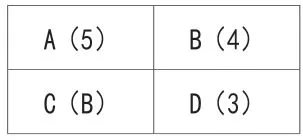
图6.2

第3类：2组颜色都相同（用2色）（AD颜色相同、BC颜色也相同）N3=A52=5×4=120种。

图7

综上知N=N1+N2+N3=120+120+20=260种。

渗透核心素养：数学建模；数学运算；数据分析

通过上述案例，笔者认为，在新高考背景下做好对学生学科素养能力的培养和提升工作，一定要在“引”上多下功夫，引导学生积极发现、探索，拓展学科知识与生产生活的实际联系，用解决实际问题的任务驱动激发学生的内驱力，唤醒学生对新知的渴求，不断积蓄参与学习的热情，让学生充分感受数学不仅是作为工具学科而存在的，数学源头里注入的生活活水，在涤荡数学美的同时，也能让我们的生产生活更加有序、高效。