周忠源

（乔治亚州大学系统董事会研究与政策分析局，美国）

1 Introduction

Density functional theoretical（DFT）method［1，2］has been widely applied to many areas in theoretical physics and chemistry［3，4］due to its computational simplicity in dealing with systems with a large number of electrons.The basis of the DFT method is Kohn-Sham（KS）equation［2］together with the key part of exchange-correlation（XC）potential［5］.Traditional XC potentials，such as local density approximation（LDA）［3，4］and generalized gradient approximation（GGA）［6-8］，are obtained by using uniform electron gas.They cannot be directly applied to the calculation of excited -state energy，especially highly excited-state energy，because of two reasons：（1）Only a few bound unoccupied states and no Rydberg states are predicted when using these potentials because they fall off too fast and do not have correct asymptotic behavior；（2）The calculated energies of the excited states with different symmetries may have the same value because these potentials are independent of symmetries such as electron orbital angular momentum and spin.

Actually，the eigenvalues of the KS equation are not rigorously the excited-state energies because the DFT method itself is a ground -state theory.However，the eigenvalues can serve as good zero-order excited -state energies provided a high-quality XCpotential is used in solving the KS equation.A number of theoretical methods have been developed along this direction.In particular，a DFT method［9，10］has been proposed based on a localized Hartree-Fock（LHF）exchange（X）potential.The LHF exchange potential is derived under the assumption that the X-only KS determinant is equal to the Hartree-Fock（HF）determinant.It only uses occupied orbitals and is dependent on the orbital symmetry.This method has been successfully applied to the ground -state calculations of atomic and molecular systems［9］.

Recently，we presented a spin -dependent localized Hartree-Fock（SLHF）DFT approach［11］for the calculation of highly and multiply excited states of atomic systems based on the LHF DFT method［9，10］and Slater's diagonal sum rule［12］.In this approach，the exchange potential is an exactly nonvariational SLHF exchange potential obtained in a similar way as the LHF potential by assuming that for excited states the X-only KS determinant is also equal to the HF determinant.This approach has been successfully used to accurately calculate the energies of multiply excited states of valence electrons of atomic systems［11］，inner-shell excited states of close-shell atomic systems［13］，and inner-shell excited states of open-shell atomic systems［14］.

In this paper，we extend the SLHF DFT approach to molecular systems and apply the approach to the calculation of potential energies of excited states of diatomic molecular systemsand H2.Because diatomic molecules are cylindrically symmetric the KS equation is transformed to the form in prolate spheroidal coordinates，in which the singularities of electron -nuclei interaction potential at two nuclei are taken good care of.Due to the singularity at the origin and longrange nature of the Coulomb potential，we use the generalized pseudospectral（GPS）method［15］to discretize the spatial coordinates and optimize the solution of the KS equation.The total potential energies ofand H2obtained from the X-only SLHF DFT calculations are surprisingly close to those of the Exact and Hartree-Fock（HF）methods.The total potential energies from the XC SLHF DFT calculations are in overall agreement with the available theoretical results at equilibrium internuclear distance.The correlation potential and energy functionals of widely-used traditional approximations，such as Lee，Yang and Parr（LYP）［7］and Perdew and Wang（PW）［8］，are explored.It is shown that the approximations underestimate the correlation energy at large internuclear distance.

2 Theoretical methodology

2.1 SLHF DFT approach for molecular systems

The spin-orbitalφjσ（r）of an electron j with spin σ（σ=αfor spin-up and β for spin-down）is determined by Kohn-Sham（KS）equation（in a.u.）

where，the local effective potential VSσ（r）=Vext（r）+VH（r）+Vxcσ（r）consists of three parts：external potential Vext（r），Coulomb electrostatic potential between electrons VH（r），and exchange-correlation potential Vxcσ（r）.The total electron number of the molecule N=∑σNσ=Nα+Nβ.

For a molecular system with M nuclei（Zi，Ri）（i=1，2，…，M），the external potential Vext（r）is given by

The Coulomb electrostatic potential between electrons is given by

where，the total electron densityρ（r）=ρα（r）+ρβ（r）and the spin -dependent electron density ρσ（r）is defined by

hereνjσis occupied number of electron on the spin -orbitalφjσ（r）.

The exchange correlation potential Vxcσ（r）=Vxσ（r）+Vcσ（r）can be separated into exchange potential Vxσ（r）and correlation potential Vcσ（r）.The exchange potential is the SLHF exchange potential given by［11］

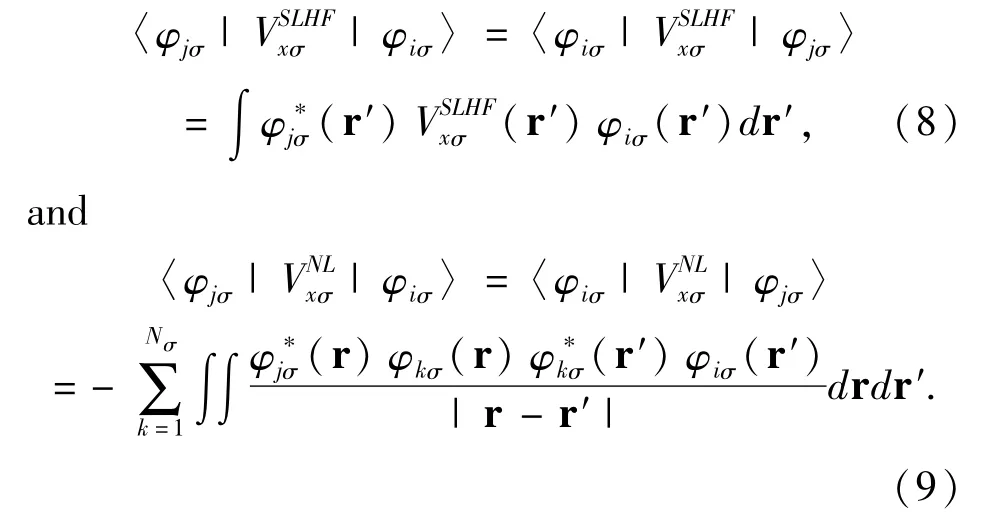
The exchange interaction only occurs among electrons with same spin.When（r）=0 in Eq.（5），the SLHF exchange potential downgrades to the Slater potential of the HF method［16］.Because（r）in Eq.（7）depends on，the SLHF exchange potentialhas to be computed self-consistently.The SLHF exchange potential determined by Eqs.（5）-（9）has an arbitrary additive constant.This constant is computed by demanding the highest-occupied-spin-orbital Nσof spin σsatisfy［11］〈φNσσ||φNσσ〉=0.

The correlation potential Vcσ（r）can be estimated from several approaches.In this work，a widelyused LYP correlation potential［7］is used.The feasibility and accuracy of correlation potentials from other approximations，such as PW correlation potential［8］，are also explored.

The single Slater determinant for a specific state of an Nσ-electron molecule can be constructed under the single determinant approximation byΦσ（r）.The total energy is a sum of kinetic-energy Ek，external-field energy Eext，Hartree energy（Classical Coulomb energy）EH，exchange energy Ex，and correlation energy Ec.They are evaluated by

and the correlation energy Ecis computed by using the LYP approximation［7］.

2.2 KS equation in prolate spheroidal coordinates for diatomic molecules

For a diatomic molecule with two nuclei（Z1，R1）and（Z2，R2），the external potential Vext（r）given by Eq.（2）is reduced to

This potential has two singularities at R1and R2.The diatomic molecule has a cylindrical symmetry.It can be very well represented in prolate spherical coordinates（η，θ，φ）（0 ≤η＜∞，0 ≤θ＜π，0 ≤φ＜2π）.Most importantly，the two singularities can be taken good are of.The relation between the prolate spherical coordinates and Cartesian coordinates（x，y，z）is x=a sin hηsinθcosφ，y=a sin hηsinθsinφ，z=a cos hηcosθ，a is constant.Due to the cylindrically symmetric property，the spin -orbitalφjσ（η，θ，φ）depends on the angleφthrough the function fm（φ）（m=0，±1，±2…）and thus can be written as

The corresponding spin -dependent density（independent ofφ）is given by

Here the quantum number m measures the component of angular momentum mħalong the molecule axis.The orbital energy only depends on λ=|m|and thus is double degenerate（corresponding to m=±λ）except forλ=0.

The orbitals are denoted byσ，π，δ，φ，… forλ=|m|=0，1，2，3，….For a homonuclear diatomic molecule the corresponding spin -orbitals are completely denoted byσg，σu，πg，πu…，where the subscripts g（even parity）and u（odd parity）represent that the spin -orbital is either unchanged or merely changed in sign when an inversion is applied to the molecule with respect to the midpoint between the nuclei（the center of the molecule）：φjσ（r）=φjσ（-r）orφjσ（r）=-φjσ（-r）.In the prolate spheroidal coordinates the g orbitals and u orbitals satisfy respectively

This condition is used to identify a specified orbital from the calculated spin-orbitals.

The molecular states are denoted by similar symbols but capital letters.For molecules with the total orbital angular momentum Λħaround the symmetry axis，its states are denoted byΣ，Π，Δ，Φ，… for Λ=0，1，2，3，….Furthermore，there are two kind ofΣstates，Σ+and Σ-，corresponding to the wave function does（-）or does not（+）change sign on reflection in a plane passing through the nuclei.So the molecular states are denoted by，，Πg，Πu，Δg，Δu，Φg，Φuand so on.The state symbols are also prefixed by a multiplicity superscript2S+1 for the resultant spin S（S=0，1/2，1，3/2，…）.For example，the ground-state and an excited-state electron configurations and molecular states of H2is1Σand 1σg1Π.For a diatomic molecule with internuclear distance R=2a，applying Eq.（15）to KS equation Eq.（1），one has

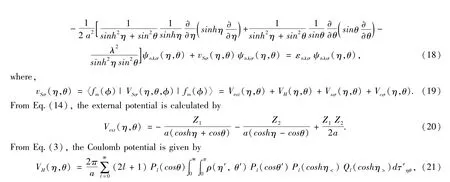
where，the expansion of1/|r-r'|in term of the first kind of associated Legendre polynomialand the second kind of associated Legendre polynomialis used，r=（η，θ，φ），r′=（η'，θ'，φ'），η＜=min（η，η'）and η＞=max（η，η'），dτηθ=a3（cosh2η-cos2θ）sinhηsinθdηdθand dr=dτ=dτηθdφ.

From Eqs.（5）-（9），the exchange potential is computed by

where，the Slater potential is given by

The correlation potential Vcσ（η，θ）is estimated from the one given by LYP approximation［7］.

The boundary conditions for solving Eq.（18）for m=even and odd are given by

and

respectively.For both m=even and odd

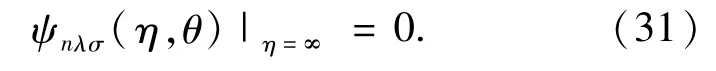
2.3 Total energy of the diatomic molecule

From Eqs.（10）-（13），after obtained the 2D spin-orbitals，the total energy is computed by E=Ek+EH+Ex+Ec.Here the kinetic energy is

and the correlation energy is estimated from the one given by LYP approximation［7］.

It is interesting to check the contributions from both Hartree energy and exchange energy to the selfinteraction energy.By setting n'm'σ'=n″m″σ″=nmσin Eq.（34）the contribution from Hartree energy is

Similarly，by setting n'm'=n″m″=nm in Eq.（35）the contribution from the exchange energy equals to-SE.As a result，the contributions from Hartree energy and exchange energy completely cancel out each other.Thus SLHF DFT approach is completely selfinteraction free.

3 Numerical algorithm and programming

3.1 Generalized pseudospectral method

On（-1 ≤x≤1，-1 ≤y≤1），a function F（x，y）is approximated by an Nx×Ny-order polynomial FNxNy（x，y）constructed by cardinal functions gi（x）and gj（y）

where，Fij=F（xi，yj）=FNxNy（xi，yj）.In the generalized Legendre-Gauss-Lobatto pseudospectral method，the cardinal function is given by

where，PNzandare Legendre polynomial and its first derivative，respectively.The collocation points zk（k=0，1，…，Nz）are determined by（zk）=0 and gk（zk'）=δkk'.

To use the pseudospectral method above to solve Eq.（18），the spin -orbital is mapped from｛（η，θ），0 ≤η＜ηmax，0 ≤θ≤π）｝ to｛（x，y），-1≤x≤1，-1 ≤y≤1 ）｝ by using mapping functions

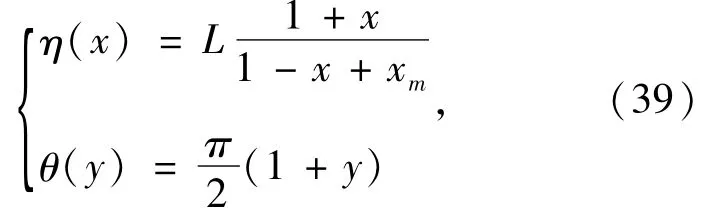
where，xm=2L/ηmax.The mapping parameter L can be used to adjust the distribution of the collocation points and thus optimize the solution of the KS equation.

3.2 Symmetric matrix eigenvalue equation

To acquire a symmetric matrix eigenvalue equation we apply variational method to the one-electron energy functional under the boundary conditions Eqs.（29）-（31）instead of directly discretizing Eq.（18）.From Eq.（1），using Eq.（15）and ∇φin the prolate spheroidal coordinates，the one-electron energy functional is calculated by（we drop the subscripts of the state in this subsection for convenience）

Using the variational method ∂G（ψ）/∂ψ*=0，the symmetric matrix eigenvalue equation is given by

where，μ=e and o for m=even and odd，respectively.The coefficients for m=even and odd are listed in List 1.where

List 1 The coefficients used in Eq.（46）.

Since all the Akk'coefficients is symmetric with respect to k↔k'，the coefficient matrix X and Y are symmetric.Using the eigenvectorχijobtained from the matrix eigenvalue equation（46），the electron orbitalψis calculated by

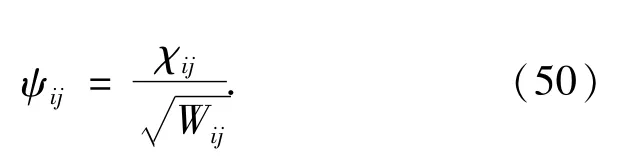
3.3 Potential and energy

In the matrix eigenvalue equation，the potential matrix elements Vij=vSσ（i，j）are calculated slefconsistently with eigenvectors χij.The external potential Eq.（20）is calculated by

The classical Coulomb potential Eq.（21）is computed by

where

The exchange potential given by Eq.（22）is

The total effective potential Eq.（19）is now computed by

where，Vcσis correlation potential given by the LYP approximation［7］.

Once the eigenvectorsχijare obtained，the total energy of the molecular system is calculated by

where，the kinetic energy Ek，external energy Eext，Hartree energy EH，exchange energy Exare calculated by

respectively，and the correlation energy Ecis calculated by the LYPapproximation［7］.In Eq.（64），Tnλσis calculated by

where，the matrix elements used in Eq.（68）are listed in List 2.

List 2 The matrix elements used in Eq.（68）.

4 Resultsand discussion

4.1 Potential energy of

4.1.1 Potentialenergy from‘Exact’ calculation

Table 1 Potential energy of ground state and excited states from the‘Exact' and SLHF DFT calculations at R=2（a.u.）.

Table 1 Potential energy of ground state and excited states from the‘Exact' and SLHF DFT calculations at R=2（a.u.）.

4.1.2 Potentialenergy fromSLHFDFTcalculation

In Fig.1，the potential energy curves from SLHF DFT calculations are plotted together with the‘Exact' results for some lower-lyingσstates.It is shown again that in the internuclear distances displayed the potential energy curves from SLHF DFT calculations are in very good agreement with the‘Exact' results.This conclusion also holds for other excited states such asπ，δ，φ，…，demonstrating that the SLHF DFT approach using the SLHF potential as exchange potential is very accurate and feasible in the calculation of the potential energies ofexcited states.

Fig.1 Potential energies of ground state 1σgand excited states 1σu，2σgand 2σufrom the‘Exact' and SLHF DFT calculations.

The SLHF DFT approach is as accurate as the‘Exact' method in the potential energy calculation is because the SLHF DFT approach is self-interaction free.To check this，we calculate various parts of the total potential energy for 1σgat R=2（a.u.）.The results are given in Table 2.It is clearly shown that the total self-energy is zero because the contributions from the exchange energy and Hartree energy cancel out each other although none of them are zero.Thus the total potential energy is a sum of kinetic energy and external energy，which is just the results of the‘Exact' calculation.

Table 2 Various parts of the total potential energy of 1σgat R=2（a.u.）.

Table 2 Various parts of the total potential energy of 1σgat R=2（a.u.）.

4.2 X-only potential energy of H2

4.2.1 Groundstate

H2is a simplest molecular system（with the equilibrium internuclear distance R≈1.4 a.u.）in which the electron correlation exists.A complete computation of the total potential energy should include the correlation energy.However，to explore the accuracy of the SLHF potential as exchange potential in DFT calculation of more than one electron molecular systems，we first perform X-only SLHF DFT calculation by neglecting the correlation effect and compare the results with those of Hartree-Fock（HF）method［18］.To that end，we include every parts in the effective potential but correlation in the calculation of H2energy.The calculated results are listed in Table 3 together with those from HF method［18］for the ground state1Σof H2at different internuclear distances.It is shown that the results are in very good agreement with those of HF method for the given internuclear distances，demonstrating that the SLHF potential as an exchange potential is also very accurate in the DFT calculation of H2ground state.

Table 3 The negative values of the X-only potential energies（in a.u.）for H2ground state Σat different internuclear distances.

Table 3 The negative values of the X-only potential energies（in a.u.）for H2ground state Σat different internuclear distances.

a：this work，b：HF method［18］.

4.2.2 Excitedstates

Success of the SLHF DFT calculation of the ground state of H2and excited states of atomic systems［11，13，14］make it confident to extend the SLHF DFT approach to the calculation of X-only potential energies of H2excited states.Systematic and accurate potential energy curves of H2excited states are useful and helpful to basic theoretical research and experimental investigations.The potential energy depends on electron spin λ，electron symmetries（g，u），and total spin S=∑si.The calculated X-only potential energies of H2ground state 11Σand singly excited states1σg1σu1Σand3Σare shown in Fig.2.The ground state potential energy curve is very close to the results of HF method［18］at available internuclear distances，as shown in Table 1.The potential energy curve of 1σg1σu1Σis a weak bound -state potential energy curve which can only hold a very limited number of bound states.While the potential energy curve of 1σg1σu3Σis a repulsive potential that does not hold any bound state.

In Fig.3，the X-only potential energy curves of H2singly excited states1σg2σg1Σand 1σg2σu1Σ and3Σare plotted.All the three are bound -state potential energy curves.The deeper potential energy curve is the one of 1σg2σg1Σand the shallower one is that of 1σg2σu1Σ.

Fig.2 X-only potential energies of H2ground state 1Σand singly excited states 1σg1σu1Σ and3Σ.

Fig.3 X-only potential energies of H2singly excitedstates1σg2σg1Σand 1σg2σu1Σ and 3Σ.

The X-only potential energy curves of H2singly excited states 1σg1πu3Π and1Π，and 1σg1πg3Π and1Πare displayed in Fig.4.These potential energy curves are also bound -state potential energy curves.The potential energy curve of 1σg1πg3Π is very close to that of1σg1πg1Π.The deeper potential energy curve is the one of 1σg1πu3Πand the shallower one is that of 1σg1πg1Π.

For higher singly excited states and doubly（or multiply）excited states，their potential energy curves are either very weak bound -state ones or repulsive ones.

4.3 Total XC potential energy of H2

Fig.4 X-only potential energies of H2singly excitedstates1σg1πu3Πand 1Π，and 1σg1πg3Πand 1Π.

A complete calculation of the potential energy should include electron correlation energy.In this section，we take the correlation energy into account in the energy calculation and explore the accuracy of the traditional approximations of correlation energy.For this purpose，we incorporate the correlation potential and energy functionals given by LYPapproximation［7］into Eq.（62）and Eq.（63）to estimate the correlation potential and energy when solving the matrix eigenvalue equation Eq.（46）.The calculated total XC potential energies of H2ground state11Σat different internuclear distances are given in Table 4 together with the results of variational method（VM）［19］.It is shown that the total XC potential energies are overall in reasonable agreement with the VM results［19］at smaller and around equilibrium internuclear distances but deviate from the VM results at larger internuclear distances.This can be seen more clearly in Fig.5，where the potential energy curves from the XC SLHF DFT calculation and the VM calculation are plotted.

Table 4 The negative values of the total XCpotential energies（in a.u.）for H2ground state 1 Σat different internuclear distances.

Table 4 The negative values of the total XCpotential energies（in a.u.）for H2ground state 1 Σat different internuclear distances.

a：this work，b：variational method［19］.

Fig.5 Potential energies of H2ground state 1 1Σ from the XC SLHF DFT approach and variational method［19］.

Obviously，the discrepancy of total potential energy between the XC SLHF DFT calculation and the VM calculation is due to the underestimation of the correlation energy from the LYP approximation at larger internuclear distances.This can be seen clearly from Table 5，where the contributions of exchange and correlation to the total potential energies from various approaches，in particular，the exact exchangecorrelation treatment（EET）with an orbital dependent exchange-correlation functional［20］，are given at equilibrium and larger internuclear distances.It is shown that the exchange energies from the XC SLHF DFT calculation are overall close to those from the EET［20］at both equilibrium and larger internuclear distances.The correlation energies from both the traditional LYP［7］and PW［8］approximations are roughly close to those of EET at equilibrium internuclear distance but greatly underestimate the correlation at larger internuclear distance.Therefore an accurate approach for correlation energy at large internuclear distances is also indispensable to the calculation of excited-state potential energy curves of diatomic molecular systems.

5 Conclusions

We proposed an SLHF DFT approach for the excited-state potential energies of molecular systems by extending the SLHF DFT approach we developed for the excited -state energies of atomic systems.This approach is applied to the calculation of the groundstate and excited state potential energies of diatomic molecular systemsand H2.The diatomic molecular system is cylindrically symmetric and its potential has two singularities.To remove the numerical difficulty of singularities we first transform the KS equation to the form in the prolate spherical coordinates.Then we applied the generalized pseudospectral method to discretize the KS equation and optimize the solution of the KS equation.Finally we solve a symmetric matrix eigenvalue equation to obtain the electron spin-orbitals and energies as well as the total potential energies.For bothand H2，the calculated Xonly potential energies from the SLHF DFT approach are in very good agreement with those of the‘Exact'and HF methods.For H2，the total XC potential energies from the SLHF DFT approach are in reasonable agreement with those of the variational method at equilibrium and small internuclear distances，but big discrepancy occurs at large internuclear distances.The reason for the big discrepancy at large internuclear distances is the underestimation of the traditional approximations to the correlation energy.To reduce the discrepancy，an accurate approximation for correlation is essential.The exact exchange-correlation treatment recently developed based on the orbital dependent exchange-correlation functional seems promising.The feasibility and accuracy of this approximation in the calculation of excited-state potential energies of diatomic molecular systems will be explored in the future.The SLHF DFT approach proposed in this work can also be directly extended to the polyatomic molecular systems once an accurate correlation potential and energy functional is available.

Table 5 Contributions（in eV）to the exchange and correlation energies in H2at equilibrium internuclear distance R=1.401 and 5.0（a.u.）.