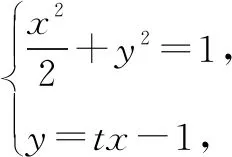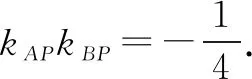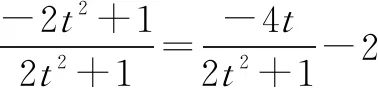朱坤城

(福建省泉州实验中学 362200)

在高考实测中，许多考生在解答解析几何中面对的困难往往是繁杂的计算，导致对解析几何的题目失去信心，实在可惜.笔者认为选择合理的运算途径，可以走出运算量大的魔圈，下面以2017年理科全国Ⅰ卷20题为例.

(1)求C的方程；

(2)设直线l不经过P2点且与C相交于A，B两点，若直线P2A与直线P2B的斜率的和为-1，证明：l过定点．

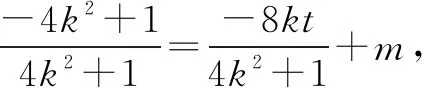
这样就避开了繁杂的计算，轻松得到定点.从解法中不难发现：这是一类由椭圆上任意一个点P(x0,y0)引出的两条直线与椭圆相交于A(x1,y1),B(x2,y2)两点的问题，具有很好的对偶性，如果能充分利用其内在的这些美学因素，必将使运算更为自然而有规可循，笔者将这类问题的解题步骤归纳为：

步骤1：设过点P的直线l:y=kx+b，联立方程组，得到关于点的一元二次方程；

步骤2：根据韦达定理求出x1,y1；

步骤3：另设直线AB的方程y=mx+t，把A点坐标代入，得到一个关于k的一元二次方程；

步骤4：再次利用韦达定理，写出k1,k2的关系(此时的k1,k2即为直线PA,PB的斜率.

为了加深对此法来解决定点问题的理解和认识，我们再看一例：

(1)求椭圆C的标准方程；

(2)设圆M:x2+(y-2)2=r2(0

因为巧设直线，我们将解题进行得如此轻松！

同样，此法也可以轻松解决定值问题，例如：

(1)求椭圆E的方程；

(2)若经过点(1,1)，且斜率为k的直线与椭圆E交于不同的两点P、Q(均异于点A)，证明：直线AP与AQ的斜率之和为定值.

(2)证明：依题意得直线PA的斜率存在并设方程为y=tx-1，P(x1,y1).

另设直线PQ的方程为y=mx+n，且直线PQ过点(1，1)，故m+n=1.

把点P的坐标代入可得：

在医学英语翻译中，句子结构复杂，修饰语繁多，各个从句在翻译时的层次也比较模糊。因此，要重点分析原文语法结构，弄清主句与从句之间的关系，才能做到译文与原文具有对等性。

我们再来看一例定值的问题：

(1)求椭圆C的方程；

(2)若P，Q是椭圆C上的两个动点，且使∠PAQ的角平分线总垂直于x轴，试判断直线PQ的斜率是否为定值？若是，求出该值；若不是，请说明理由．

(2)证明：依题意得直线PA的斜率存在并设方程为y-1=k(x-2)，P(x1,y1).

得(4k2+1)x2+8k(1-2k)x+4(1-2k)2-8=0，

另设直线PQ的方程为y=tx+m，把点A的坐标代入可得：

以下再给出两个定值的问题：

(1)求椭圆E的方程；

设过点P的直线方程为y=k(x+2)，联立方程组

整理得12k2+12tk-3=0.

(1)求椭圆E的方程；

(2)若直线DP与E交于另一点Q，直线BP、BQ分别与x轴交于点M、N,试判断|OM|·|ON|是否为定值？

(2)设过点B的直线方程为y=tx+1，联立方程组

分析近年来的高考数学试题，发现解析几何在高考试题中必有次压轴题，从学生解答压轴题的情况看，究其原因，往往由于或方法选择不当或运算不合理造成中途搁浅或结果出错.在教学过程中，也有这样的感觉，学生解题很少讲究策略或解题技巧，拿到题目就瞎撞乱碰，套路化解题，不讲究运算是否合理.因此，研究如何增强解析几何的解题策略、技巧意识，提高运算的速度，优化计算就可以帮助学生轻松拿分，增加学习的乐趣！