曾凡洋, 田 甜

战略支援部队信息工程大学, 郑州450001

1 引言

Cube 攻击由 Dinur 和 Shamir 在 2009 年欧密会上提出[1], 是对称密码算法的重要分析方法之一.特别地, 对于 Trivium-like 系列算法, 即 Trivium 算法[2]、Kreyvium 算法[3]以及 TriviA-SC 算法[4,5],cube 攻击是最有效的密钥恢复方法之一.近两年,关于cube 攻击的研究有较大进展.目前,针对Triviumlike 系列算法的cube 攻击可分为实验 cube 攻击 (或传统cube 攻击)[1]、基于分离性质的cube 攻击[6]、相关 cube 攻击[7].

序列密码的输出密钥流比特可以看作关于密钥和IV 变元的多项式f(Key,IV),其中Key 表示密钥变元,IV 表示IV 变元.在cube 攻击中,选择一组活动IV 变元的子集I,称为cube 变元.非cube 变元一般固定为常值.当cube 变元取遍所有可能的0/1 组合时, 对f(Key,IV) 求和得到关于密钥和非cube 变元的一个多项式pI(Key,IVI), 其中cube 变元的取值集合称为一个cube, 记为CI, 多项式pI(Key,IVI)称为CI的超多项式(superpoly).Cube 攻击中通过在线获得超多项式pI(Key,IVI) 的值来建立关于密钥变元的方程.由于在序列密码中, f(Key,IV) 是一个非常复杂的多项式(变元多、代数次数高、未知代数正规型), 如何求解有用的超多项式是cube 攻击的一个难点.

实验 cube 攻击也即 Dinur 和 Shamir 在 2009 年欧密会上提出的 cube 攻击[1].在实验 cube 攻击中, 攻击者通过黑盒布尔函数的低次检测方法来寻找具有低次超多项式的cube, 从而建立关于密钥变元的低次方程组.已有结果均为线性或二次超多项式.在文[1]中, 对于767-轮Trivium, 作者利用线性检测给出了 35 个线性超多项式.在文 [8]中, 作者首次将二次检测引入到 cube 攻击中.针对 709-轮 Trivium,作者给出了 41 个线性超多项式和38 个二次超多项式.在文 [9]中, 作者对于Trivium 算法的 cube 攻击给出了两个改进.首先, 利用Meobius 变换, 作者可以同时对一批cube 进行检测.其次, 作者给出了一个递归方法来构造具有线性超多项式的cube.对于799-轮Trivium, 作者给出了12 个线性超多项式和6 个二次超多项式.在文 [10]中, 针对 Trivium-like 算法, 作者利用线性化技术, 给出了一种检测非线性超多项式的新方法, 从而容易获得更多 Trivium-like 算法的二次超多项式.对于 802-轮 Trivium, 他们给出 6个线性超多项式和 2 个二次超多项式; 对于 776-轮 Kreyvium, 他们给出 8 个二次超多项式; 对于 862-轮TriviA-SC-v2, 他们给出 12 个线性超多项式和 3 个二次超多项式.这是目前文献中实验 cube 攻击给出最高轮数超多项式.

在实验cube 攻击中, 对于一个d 维cube, 至少需要运行2d次加密运算, 从而受计算资源的限制, 对于能够进行实验检测的cube, 维数通常不会超过40.在2017 年美密会上, Todo 等给出了基于分离性质(division property) 的 cube 攻击[6].这一攻击方法的明显优点是可以利用高维数 cube 分析算法的安全性, 例如大于70 维的cube.分离性质是2015 年欧密会上提出的分组密码积分区分器的一种搜索技术, 并随后用于全轮 MISTY1 分组密码的分析.在 cube 攻击中引入分离性质, 可以利用 MILP 求解器计算超多项式中可能出现的密钥变元, 进而给出cube 攻击的理论复杂度估计.文[6]中对832-轮Trivium, 给出了一个 72 维 cube, 其超多项式至多包含 5 个密钥变元, 以大约 277的时间复杂度至多恢复 1 比特密钥信息.另外, 文 [11]中针对 872-轮 Kreyvium, 给出一个 85 维 cube, 其至多包含 39 个密钥变元, 以大约2124的时间复杂度至多恢复1 比特密钥信息.在文[12]中, 作者对[6]中的工作进行了若干技术上的改进,包括更准确地找到非常值IV 变元的赋值以及降低恢复超多项式代数正规型的复杂度.文 [12]对839-轮Trivium, 给出一个78 维cube, 其超多项式至多包含1 个密钥变元, 从而以279的时间复杂度至多恢复1比特密钥信息.文 [12]对文 [11]中给出的 872-轮 Kreyvium 的 85 维 cube, 将计算复杂度降低至 294.61;对 891-轮 Kreyvium, 给出一个 113 维 cube, 其超多项式是平衡的且至多包含 20 个密钥变元, 以 2120.73的时间复杂度至多恢复1 比特密钥信息.上述基于分离性质的cube 攻击结果中, 当超多项式实际为常值多项式时, 密钥恢复攻击退化为区分攻击.

在 2018 年欧密会上, Liu 等提出相关 cube 攻击方法[7].在相关 cube 攻击中, 攻击者利用文 [13]中提出的代数次数估计方法, 找到一组关于密钥的低次多项式{g1,g2,··· ,gu} 满足超多项式 p 可以形式地表示成其中 fi是未知代数正规型的布尔函数.然后, 攻击者通过实验测试, 获得 p 的取值与gi取值之间的条件相关概率Pr(g = b|p).在获得真实密钥下超多项式p 的值后, 可以得到一些关于密钥变量的概率方程.对于 805-和 835-轮 Trivium, 文 [7]中给出的相关 cube 攻击可以分别恢复约 7 个密钥比特信息和5 个密钥比特信息, 数据复杂度245, 预处理时间复杂度是251, 在线时间复杂度是244.

注意到在文 [1]中, 利用线性检测, 针对减轮 Trivium 算法, 作者给出了大量具有线性超多项式的cube.在这些给出的 cube 中, 存在滑动的现象, 即存在 IV 变元集 {v0,v1,··· ,vm−1} 的子集 I1和 I2, 使得 CI1对于 zt的超多项式 pI1(k1,k2,··· ,kn−1) 和 CI2对于 zt+1的超多项式 pI2(k0,k1,··· ,kn−2) 满足 pI2(k0,k1,··· ,kn−2)= σ(pI1(k1,k2,··· ,kn−1)), 其中 ki表示密钥变量, I2={vi−1|vi∈ I1}, σ 将 ki映射到ki−1.由于Kreyvium 和TriviA-SC(v1 和v2)算法与Trivium 算法具有非常类似的结构,这使得其cube 攻击与Trivium 算法具有较为相似的性质.对于给定的I1如果我们能够快速判断出其具有滑动性, 那么我们就能够直接根据 CI1对于 zt的超多项式 pI1(x1,x2,··· ,xn−1) 计算出 CI2对于 zt+1的超多项式 pI2(x0,x1,··· ,xn−2).因此, 本文主要关注 Trivium-like 算法中 cube 的滑动性.首先, 我们通过对比分析第0 时刻内部状态S0和第1 时刻内部状态S1的代数正规型(Algebraic Normal Form, ANF),从理论上给出了cube 具有可滑动性的一个充分条件.进一步, 我们将充分条件的判断转化为MILP 模型的可行性判断, 在实际分析中基于MILP 求解器能够快速判断出具有滑动性的cube.最后, 我们将充分条件应用到实验 cube 攻击、基于分离性质的 cube 攻击和相关 cube 攻击, 验证了方法的正确性并在实验cube 攻击中得到了一个 803-轮 Trivium 的新结果.

本文剩余部分安排如下: 第 2 节介绍了 cube 攻击、Trivium-like 算法、MILP 模型和可滑动 cube的概念.在第 3 节中, 针对 Trivium-like 算法, 我们给出了一个 cube 具有滑动性的充分条件.在第 4 节中, 介绍了如何将充分条件应用到实验cube 攻击、基于分离性质的cube 攻击和相关cube 攻击中, 并给出了相关结果.第5 节总结了全文.

2 预备知识

2.1 Cube攻击

在 cube 攻击中, 目标密码算法的输出比特 z 被看作关于 IV 变元 IV = (v0,v1,··· ,vm−1) 和密钥变元 Key = (k0,k1,··· ,kn−1) 的布尔函数, 即 z = f(IV,Key).选定一个 IV 变元的子集I ={vi0,vi1,··· ,vi|I|−1}, 令 tI是 I 中变元的乘积, 即 tI=vi0vi1···vi|I|−1, 则 z 可以表示为

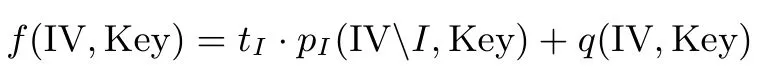
其中多项式 pI不含 I 中的变元, 多项式 q(IV,Key) 中的任意项不被 tI整除.令是 I 中变元的一个取值集合满足I 中每个变元独立取遍F2中元素, 则有

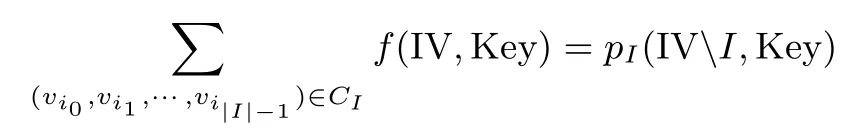
在 cube 攻击中, I = {vi0,vi1,··· ,vi|I|−1} 中变元称为 cube 变元, 其余 IV 变元称为非 cube 变元.非cube 变元总是设为常值并且通常设置为 0 常值.多项式 pI(IVI,Key) 称为超多项式.显然, 当给定非cube 变元取值后, 例如 0 常值, 则 pI(0,Key) 是关于密钥的一个多项式.在 cube 攻击中, 通过恢复超多项式来建立关于密钥变元的方程.最后, 包含 cube 变元所有 2|I|种可能取值 (非 cube 变元固定为常值)的集合 CI称为一个|I|-维 cube.

Cube 攻击包含离线阶段和在线阶段.

离线阶段: 由于函数f(IV,Key) 的代数正规型是未知的, 攻击者通过线性/二次检测等黑盒布尔函数的检测方法来寻找具有低次超多项式的cube 以及恢复超多项式的代数正规型.

在线阶段: 根据离线阶段找到的 cube 和超多项式, 攻击者通过查询密码机确定其超多项式在当前密钥下的函数值, 从而建立关于密钥变元的低次方程组.通过求解方程组, 攻击者可以恢复密钥变元的部分或全部信息.

2.2 Trivium-like算法

本小节主要介绍 Trivium-like 算法, 主要包括 Trivium 算法、Kreyvium 和 TriviA-SC 算法.

2.2.1 Trivium 算法

Trivium 算法是由 Canniere 和 Preneel 设计的面向硬件实现的流密码算法.Trivium 算法包括三个寄存器, 级数分别为 93、84 和 111, 内部状态长度为 288 比特, 分别用 s1,s2,··· ,s288表示.密钥 Key和 IV 长度均为 80 比特, 分别用 k0,k1,··· ,k79和 v0,v1,··· ,v79表示.初始化时, 首先, 用密钥和 IV 填充前两个寄存器, 其余位置均填充常值; 然后, 内部状态更新 1152 轮.初始化完成后, 内部状态每更新一拍, 输出1 比特密钥流, 由内部状态6 个位置的比特异或得到.算法1 给出了Trivium 算法的密钥流生成的伪代码描述.

?

2.2.2 Keryvium 算法

Kreyvium 算法是Canteaut 等人设计的Trivium 算法的128 比特密钥版本, 目标在于高效实现同态加密中的同态密文压缩[3].Kreyvium 算法的密钥和IV 都是128 比特, 与Trivium 算法的不同之处在于:除了和Trivium 算法完全一样的288 比特主寄存器以外, 还添加了两个128 比特的寄存器来分别存储密钥和IV, 密钥寄存器和IV 寄存器只做循环移位更新; 在288 比特主寄存器更新时, 不断以异或加的方式添加密钥和 IV 比特.因此 Kreyvium 内部状态为 544 比特, 由 5 个长度为 93、84、111、128 和 128 比特的寄存器组成.算法2 描述了Kreyvium 的密钥流生成算法的伪代码描述.

2.2.3 TriviA-SC 算法

TriviA-SC 算法由 Chakraborti 等人设计的流密码算法, 它是 CAESAR 竞赛的第二轮候选认证加密算法 TriviA 的基础组件.TriviA-SC 算法有两个版本, 即 TriviA-SC-v1 和 TriviA-SC-v2.在下文中,TriviA-SC 算法都指的是 TriviA-SC-v2 算法.TriviA-SC 算法的密钥和 IV 都是 128 比特, 内部状态由三个长度为 132、105 和 147 比特寄存器构成, 总共为 384 比特.采用和 Trivium 算法相似的更新函数,初始化轮数也是1152.算法3 给出了TriviA-SC 的密钥流生成算法的伪代码描述.

?

?

2.3 混合整数线性规划

线性规划(Linear Programming) 是一类实数域上的优化问题, 其标准形式如下

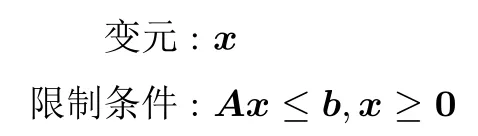
其中 x ∈Rn,A ∈Rm,n,b ∈Rm,c ∈Rn.若变元 x 的部分或全部取值限制在整数范围, 则该优化问题称为混合整数线性规划(Mixed Integer Linear Programming, MILP).求解MILP 模型的求解器有Gurobi[14]和CPLEX[15]等.如果模型有解, 则求解器会返回一个解; 如果模型没有解, 则求解器返回不可行.若模型没有目标函数, 则求解器仅返回是否可行.

2.4 可滑动cube

为表述方便, 在介绍可滑动 cube 的定义以前, 先介绍符号 σ.设 X = {x0,x1,··· ,xn−1} 是一组变元, 对于任意非空子集 U ={xi1,xi2,··· ,xim} ⊆ X, 记

上述变元集合可以是 IV 变元, 也可以是密钥变元.进一步, 关于变元集 U 的一个布尔函数f(xi1,xi2,··· ,xim), 记

也即 σ(f(U))=f(σ(U)).我们规定 σ(0)=0,σ(1)=1.下面我们定义可滑动 cube.

定义 1 (可滑动 cube)设 I ={vi0,vi1,··· ,vi|I|−1}(ij⩾ 1,j =0,1,··· ,|I|−1) 是一组 IV 变元集,并设 Cube CI关于算法在 t 时刻的输出zt的超多项式为pI.如果Cube Cσ(I)关于该算法t+1 时刻的输出 zt+1的超多项式为 pσ(I)=σ(pI), 则称 CI为可滑动 cube, 并称 (CI,Cσ(I)) 为滑动 cube 对.

例 1取 I = {v3,v9,v14,v20,v23,v27,v31,v47,v48,v63,v70,v72}, Cube CI关于 Trivium 算法 673轮输出比特的超多项式为 pI= k31．容易验证, Cσ(I)关于 Trivium 算法 674 轮输出比特的超多项式为pσ(I)=k30= σ(pI).故, CI为可滑动 cube, (CI,Cσ(I)) 为滑动 cube 对.

3 可滑动cube的充分条件

在本节中, 针对 Trivium-like 算法, 我们给出了可滑动 cube 的一个充分条件.因为TriviA-SC 算法和 Kreyvium 算法的结构与 Trivium 算法结构相似度较高, 所以, 在本节中我们只对 Trivium 算法的可滑动cube 的充分条件给出了详细证明.对于 TriviA-SC 算法和 Kreyvium 算法, 可滑动 cube 的充分条件的证明可以类似得出.

3.1 Trivium算法可滑动cube的充分条件

本节讨论 Trivium 算法可滑动 cube 的充分条件.记 Trivium 算法密钥变元为 Key = {k0,k1,··· ,k79}, IV 变元为 IV={v0,v1,··· ,v79}, 第 t 时刻内部状态比特为第 t 时刻的输出比特为zt.显然, 每个内部状态比特都可以看作Key 和IV 的布尔函数, 即

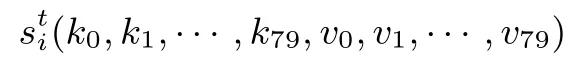
若选定一组 cube 变元 I ={vi0,vi1,··· ,vi|I|−1}⊆IV, 非 cube 变元固定为常值 0 或 1, 则我们用符号

定义 2设 I = {vi0,vi1,··· ,vi|I|−1} ⊆ IV 是一组 cube 变元, 集合 J ⊆ {1,2,··· ,288}.对于Trivium 算法的连续两个内部状态若对每个k ⊆ J 有

成立, 则称 (St,St+1) 关于 (I,J) 是滑动状态, 其中 d ∈{0,1}.上述(1)式也简写为

引理 1设 I = {vi0,vi1,··· ,vi|I|−1} ⊆ IV 是一组 Cube 变元, 集合 J ⊆ {1,2,··· ,288}, 并且(St,St+1) 关于 (I,J) 是滑动状态.对于到 F2的任意布尔函数 F(X)=F(x0,x1,··· ,xn−1), 有

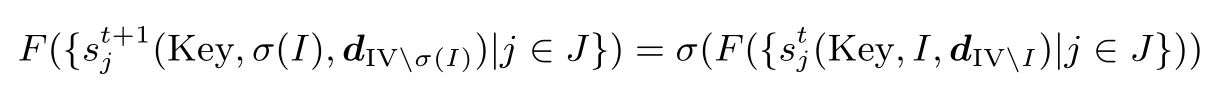
证明:不妨设F(X) 的代数正规型为:

集合 J ={j0,j1,··· ,jn−1}, 则有

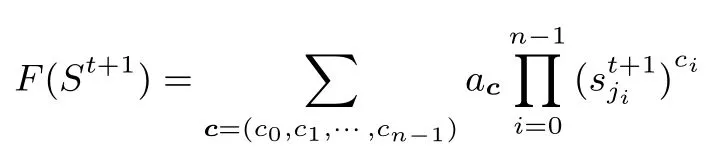
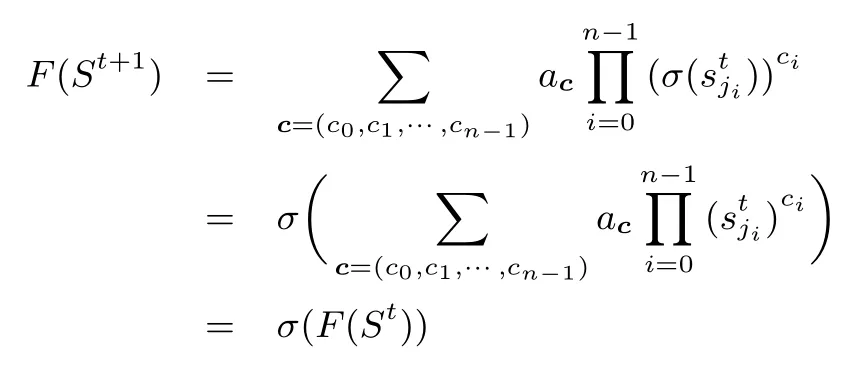
设 I ⊆ IV 是一组 cube 变元.对于 I 和 σ(I), 记它们对 zt和 zt+1的超多项式分别为 pI和 pσ(I).由于 zt=F(St) 且 zt+1=F(St+1), 那么根据引理1, 若 J ={1,2,··· ,288} 且存在时刻 t 满足 (St,St+1)关于 (I,J) 是滑动状态, 那么 zt+1= σ(zt), 从而有 pσ(I)= σ(pI).注意到在实际中, 超多项式 pI并不一定与每一个内部状态都相关, 所以考虑cube 的可滑动性时并不需要J ={1,2,··· ,288} 这么苛刻的条件.

为了给出Trivium 算法可滑动cube 的充分条件, 我们首先考察Trivium 算法第0 时刻内部状态S0和第 1 时刻内部状态 S1, 具体见表1.在表1 中, 我们给出了S0和S1中每一个状态比特关于 IV 变元和密钥变元的ANF.

定理 1 (充分条件)设 I = {vi0,vi1,··· ,vi|I|−1} ⊆ IV 是一组 IV 变元, 令 Keynew= Key ∪{knew0,knew1,knew2}, 并且在初始化时令设 Trivium 算法第 t时刻输出zt(I,0IVI,Keynew) 关于CI的超多项式为pI.若以下两个条件成立:

(i) I 中不包含 v0,v69,v78;

(ii) pI中不包含k0,knew0,knew1,knew2;

则 (CI,Cσ(I)) 是滑动 cube 对, 即 Cσ(I)关于 zt+1(σ(I),0IVσ(I),Key) 的超多项式为 pσ(I)= σ(pI).

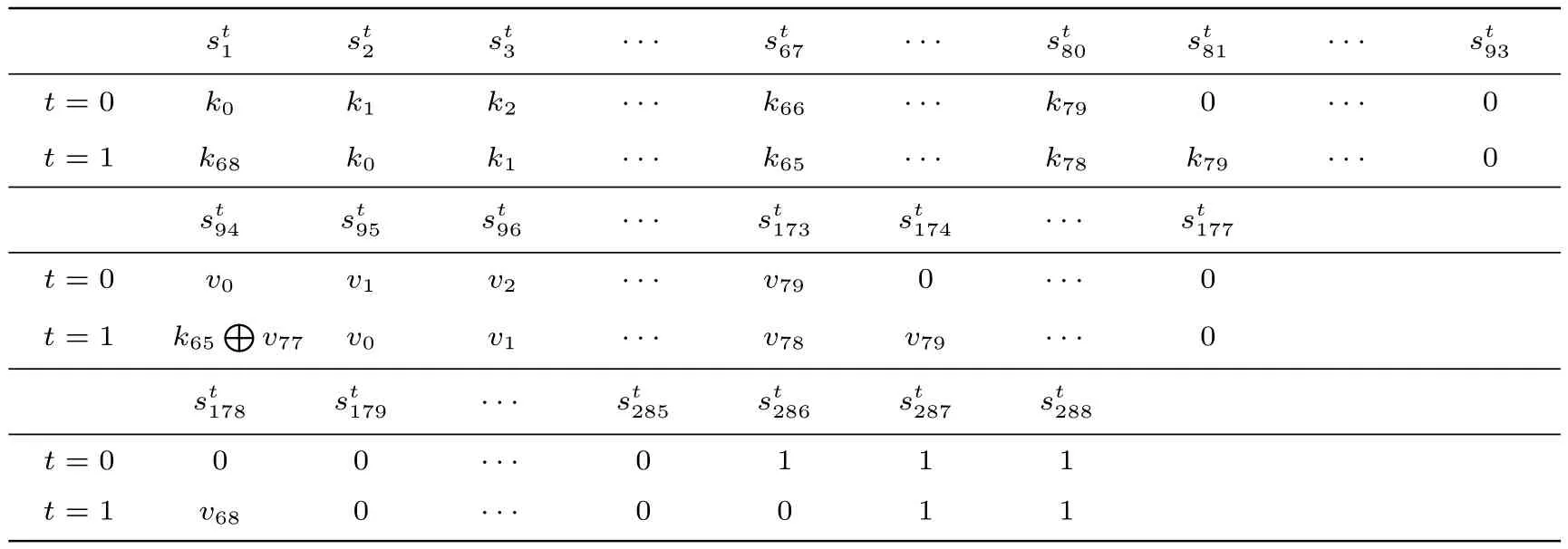
表1 Trivium 算法第 0 时刻与第 1 时刻内部状态Table 1 Internal states of Trivium at Time 0 and Time 1

表2 Trivium 算法添加新变元后第0 时刻与未添加新变元第1 时刻内部状态Table 2 Internal state with new variables at Time 0 and internal state without new variables at Time 1 of Trivium

证明:观察表2 可以发现,对于j{1,81,94,174,178,286},均有成立.由于v0,v69,v78不属于 I, 于是 v68,v77不属于 σ(I).因此, 对于 S0可以令 v0,v69,v78等于 0, 而对于 S1可以令 v68,v77等于 0.又根据定义1 可知 v79不会属于 σ(I), 故可以令 S1中 v79等于 0.从而, 有下述等式成立

我们在表3 中给出了满足定理条件时的S0和S1.观察表3 可得

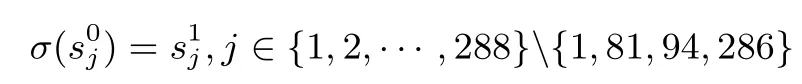
于是, zt(I,0IVI,Keynew) 可以表示成如下唯一形式

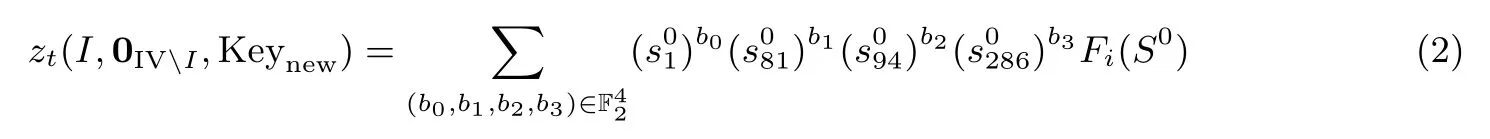
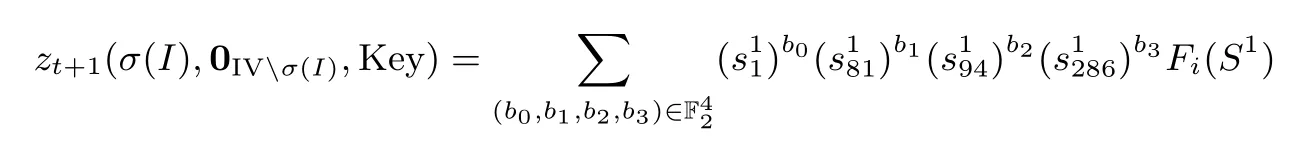
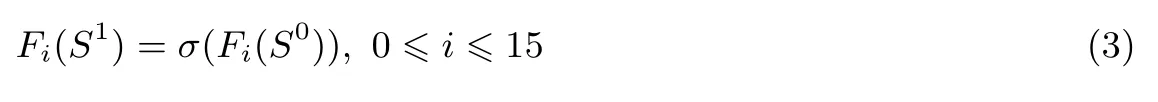
由定理条件可知, CI对于 zt的超多项式 pI不包含 k0,knew0,knew1,knew2, 由式(2)知 tI= ∏i∈Ivi只能出现在分量函数F0(S0) 中, 也即

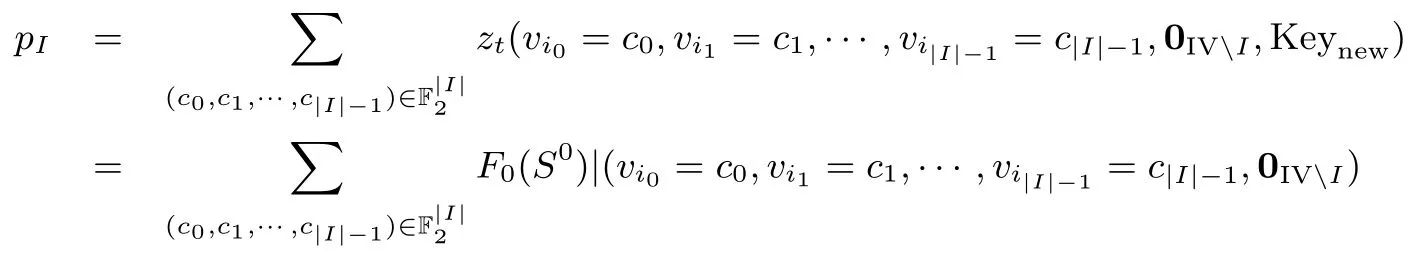
又由式(3)知 Fi(S1)= σ(Fi(S0)),0 ⩽ i ⩽ 15, 所以 tσ(I)出现在 Fi(S1) 中当且仅当 tI出现在 Fi(S0) 中.从而, tσ(I)只能出现在 F0(S1) 中, 即

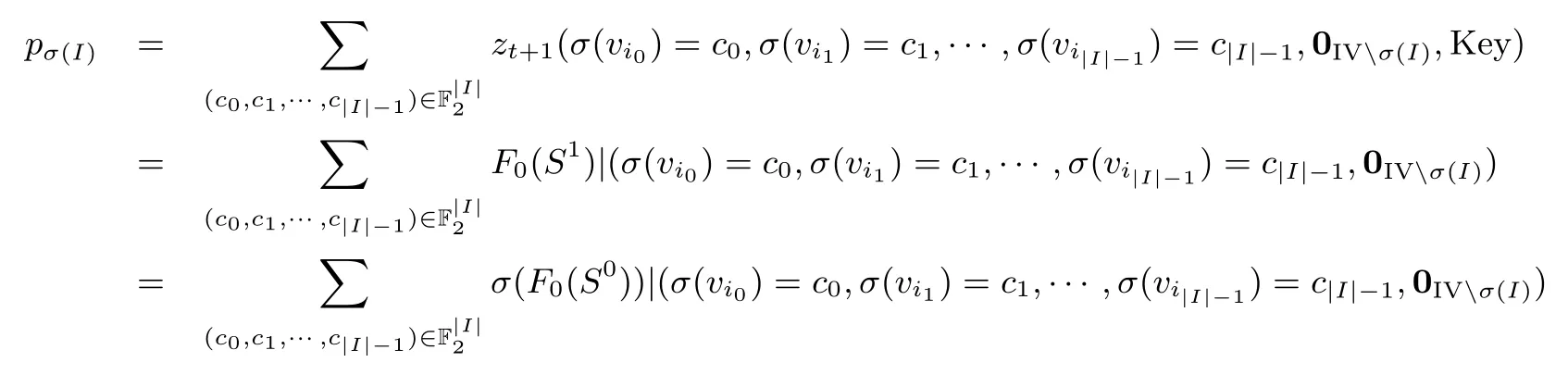
这表明 pσ(I)= σ(pI).故 (CI,Cσ(I)) 为滑动 cube 对.

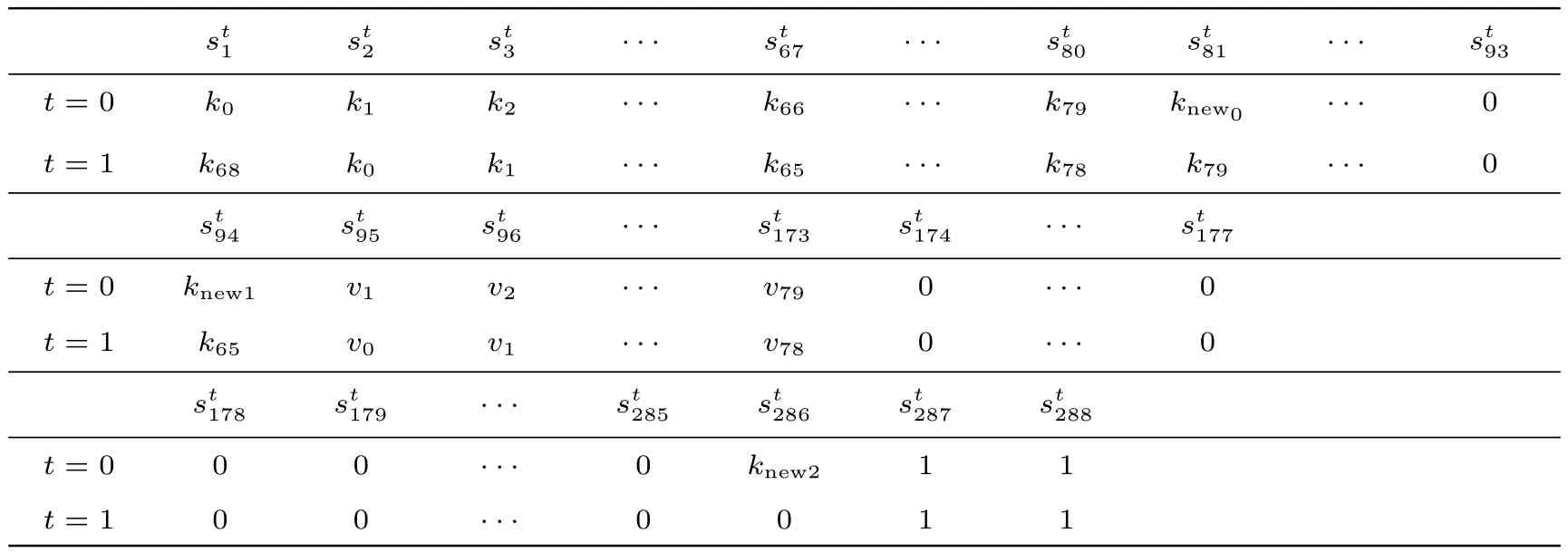
表3 满足定理1 条件时Trivium 算法第0 时刻与第 1 时刻内部状态Table 3 Internal states at Time 0 and Time 1 of Trivium when Theorem 1 is satisfied

3.2 Kreyvium算法和TriviA-SC算法可滑动cube的充分条件

在这一小节中, 针对Kreyvium 算法算法和TriviA-SC 算法, 我们直接给出可滑动cube 的充分条件.Kreyvium 算法第 0 时刻与第 1 时刻的内部状态如表4 所示, 其可滑动 cube 的充分条件由定理2 给出;TriviA-SC 算法第 0 时刻与第 1 时刻的内部状态如表5 所示, 其可滑动 cube 的充分条件由定理3 给出.

定理 2设 I = {vi0,vi1,··· ,vi|I|−1} ⊆ IV 是一组 IV 变元, 令 Keynew= Key ∪{knew0,knew1,knew2}, 并且在初始化时令设 Kreyvium 算法第 t 时刻输出zt(I,0IV(I∪{v0,v69}),1{v0,v69},Keynew) 关于 CI的超多项式为 pI.若以下两个条件成立:

(i) I 中不包含 v0,v69,v78,v83,v84;

(ii) pI中不包含k0,knew0,knew1,knew2;

则 (CI,Cσ(I)) 是滑动 cube 对, 即 Cσ(I)关于 zt+1(σ(I),0IV(σ(I)∪{v127,v68}),1{v127,v68},Key) 的超多项式为 pσ(I)= σ(pI).

定理 3设 I = {vi0,vi1,··· ,vi|I|−1} ⊆ IV 是一组 IV 变元, 令 Keynew= Key ∪{knew0,knew1,knew2}, 并且在初始化时令设 Trivia-SC 算法算法第 t 时刻输出zt(I,0IVI,Keynew) 关于CI的超多项式为pI.若以下两个条件成立:

(i) I 中不包含 v0,v66,v120;

(ii) pI中不包含k0,knew0,knew1,knew2;

则 (CI,Cσ(I)) 是滑动 cube 对, 即 Cσ(I)关于 zt+1(σ(I),0IVσ(I),Key) 的超多项式为 pσ(I)= σ(pI).

表4 Kreyvium 算法第 0 时刻与第 1 时刻内部状态Table 4 Internal states of Kreyvium at Time 0 and Time 1

4 可滑动cube充分条件的验证与应用

在第3 节中, 我们从理论上给出了可滑动cube 的充分条件.本节讨论在实际中如何验证可滑动cube的充分条件, 方法的正确性已经过大量实验验证.并且, 我们尝试对已有文献中列举的cube 攻击最好结果进行了滑动性的判断.

表5 TriviA-SC 算法第 0 时刻与第 1 时刻内部状态Table 5 Internal states of TriviA-SC at Time 0 and Time 1

4.1 基于MILP的验证方法

根据上文给出的 Trivium-like 算法可滑动cube 的充分条件, 我们可以快速判断某些 cube 是否具有滑动性, 如果具有滑动性, 那么我们可以直接获得一些新的密钥方程, 而无需其他的操作.下面我们将介绍如何具体判断充分条件是否成立.

我们仍以 Trivium 算法为例.由定理1 知, 充分条件需满足: (i) I 中不包含 v0,v69,v78; (ii) pI中不包含 k0,knew0,knew1,knew2.对于给定的 Cube CI, 条件 (i) 可以直接判断 cube 变量中是否含有变量 v0,v69,v78.而对于条件 (ii) 的判断, 我们转化为 MILP 模型来解决, 转化的理论依据由文 [6]中的Proposition 4 给出.

定理 4[6]设 f(IV,Key) 为 IV 变元 IV=(v0,v1,··· ,vm−1) 和密钥变元 Key=(k0,k1,··· ,kn−1)的多项式, 集合 I = {vi1,vi2,··· ,vi|I|} 为 cube 变元集合, lI= (l0,l1,··· ,lm) 为 m 维的比特向量满足IVlI= tI= vi1,vi2,··· ,vi|I|, 其中 vi∈ I, 则 li= 1, 否则 li= 0.设 eλ为 n 维比特向量 (第 λ 比特为1, 其余比特为 0) 满足 Keyeλ=kλ.若没有满足 (eλ,lI)1 的分离路径 (division trail), 则 CI的超多项式 pI与变元 kλ无关, 也即 kλ不出现在 pI的代数正规型中.

根据定理4, 对于 Trivium 算法, 我们将判断 cube 的可滑动性转化为求解 MILP 模型.对于给定的Cube CI, 通过求解MILP 模型来判断是否存在满足(eλ,lI)1(λ =0,new1,new2,new3) 的分离路径.如果均不存在这样的分离路径, 则变元k0,knew0,knew1,knew2不会出现在Cube CI的超多项式中.那么,CI一定是可滑动的 cube.值得注意的是, 即使存在满足 (eλ,lI)1(λ = 0,new1,new2,new3) 的分离路径, 也并不能说明变元 k0,knew0,knew1,knew2一定出现在 CI的超多项式中, CI仍然有可能是可滑动的.因此, 上述基于 MILP 模型的判断方法, 可能会丢掉一些可滑动 cube, 但并不会影响正确性, 即通过MILP 检测的一定满足可滑动的充分条件.关于分离性质、分离路径以及如何建立求解分离性质的MILP模型, 请参见文献[6,11].

为了说明利用求解 MILP 模型来判断可滑动 cube 的有效性, 我们对 672-轮 Trivium 做了大量实验验证.首先, 我们通过低次检测寻找到许多具有线性和二次超多项式的 cube (cube 变量中不包含v0,v69,v78), 然后对这些 cube 求解 MILP 模型, 仍然有大量 cube 满足其超多项式不包含 k0,knew0,knew1,knew2.我们从中选取部分放在表6 中.对于这些 cube, 我们根据定理1 计算出滑动后的 cube 及其超多项式, 具体见表7.对于滑动后的每组 cube, 我们随机选取了1000 组密钥值对超多项式进行检验, 发现对cube 求和所得值与超多项式的值完全一致.这就表明了利用求解MILP 模型来判断cube 的滑动性的有效性.

4.2 滑动cube的应用

利用求解分离性质的 MILP 模型, 我们将可滑动 cube 的充分条件应用到已有文献中针对 Trviumlike 算法给出的攻击结果, 包括实验 cube 攻击、基于分离性质的 cube 攻击和相关 cube 攻击, 最终在实验 cube 攻击中获得了一个803-轮 Trivium 的新结果.

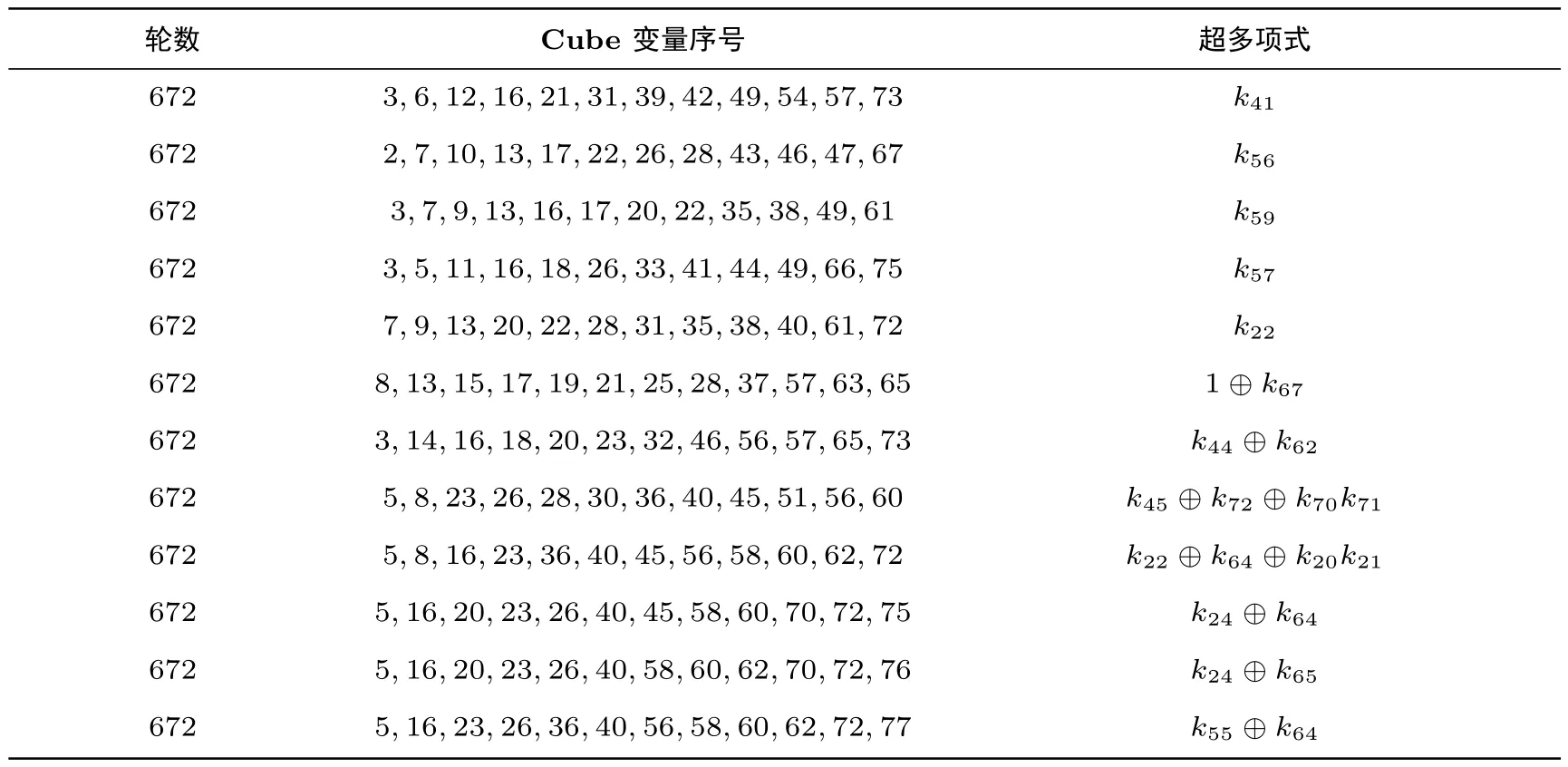
表6 672-轮 Trivium 超多项式中不包含 k0,knew0,knew1,knew2 的 cubeTable 6 Cubes whose superpolies do not contain k0,knew0,knew1,knew2 for 672-Trivium

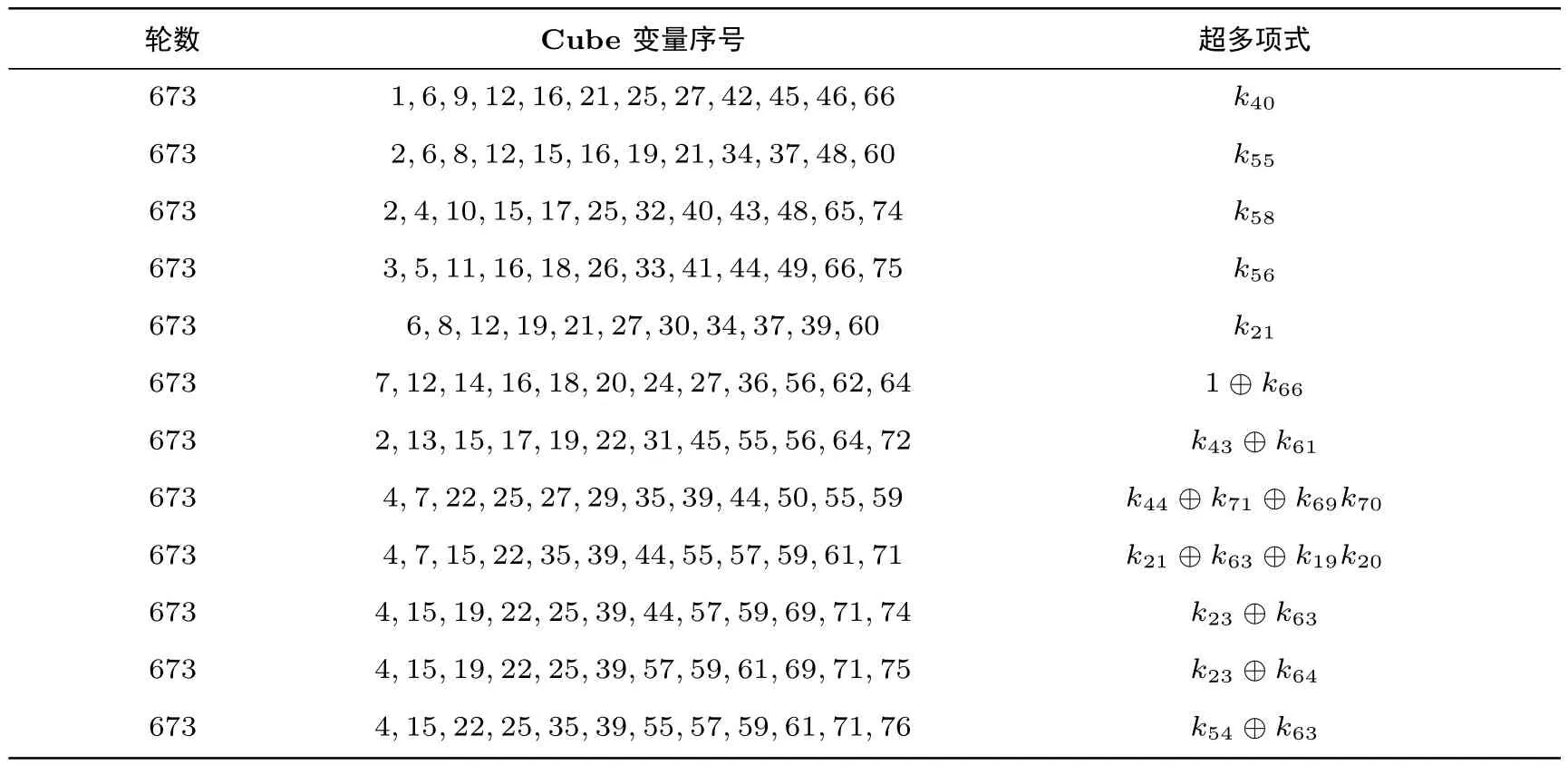
表7 滑动后的cube 及其超多项式Table 7 Cubes and their superpolies after sliding

4.2.1 实验 cube 攻击

在文[10]中, 对于802-轮Trivium, 作者给出6 个线性的超多项式和2 个二次超多项式; 对于776-轮Kreyvium, 作者给出 8 个二次超多项式; 对于 862-轮 TriviA-SC, 作者给出 12 个线性超多项式和 3 个二次超多项式.这是目前文献中实验cube 攻击给出最高轮数超多项式.对于这些cube 我们利用可滑动cube 的充分条件, 依次判断了其是否具有滑动性, 最终我们获得了减轮803-轮Trivium 一个新的cube 及超多项式, 具体结果见表8.

4.2.2 基于分离性质的cube 攻击

在文献 [11,12]中, 针对 Trivium 算法和 Kreyvium 算法, 作者给出的 cube 中都包含 IV 变量 v0, 这已经不满足可滑动cube 充分条件中cube 变量不能包含v0的规定.因此利用充分条件, 我们无法判断出这些cube 的可滑动性.

表8 803-轮 Trivium 的 cube 及超多项式Table 8 Cube and its superpoly for 803-round Trivium

4.2.3 相关 Cube 攻击

在文 [7]中, 作者在 835-轮 Trivium 的相关 cube 攻击中, 给出 28 个 cube 及其基多项式.根据定理1, 若cube 满足滑动性, 则超多项式具有滑动性.由于基多项式是超多项式的一部分, 所以基多项式也具有滑动性.我们对于这 28 个 cube 进行了可滑动性判断, 最终得到 837-轮的 1 组 cube 及其基多项式.具体结果见表9.但这组 cube 并不是一个新的cube, 在文 [7]中, 作者已经给出了这组cube 及其基多项式, 这与我们利用滑动性给出的结果是一致的.

表9 837-轮 Trivium 的 cube 和基多项式Table 9 Cube and its basis for 837-round Trivium

5 结论

在本文中, 针对 Trivium-like 算法, 我们研究了 cube 的可滑动性.首先, 针对 Trivium-like 算法, 我们给出了 cube 可滑动性的充分条件.其次, 我们将充分条件应用到实验 cube 攻击、基于分离性质的cube 攻击和相关cube 攻击, 验证了方法的正确性并最终在实验cube 攻击中得到了一个803-轮Trivium的新结果.希望本文中对cube 滑动性质的研究, 能够为 cube 攻击中在恢复密钥信息时提供一些新的攻击思路.此外, cube 的滑动性与算法的初态的填充方式有较大联系, 希望本文的研究能为算法设计提供一定的借鉴意义.