Yanxu Su, Qingling Wang, and Changyin Sun

Abstract—In this paper, we study the consensus problem for a class of linear multi-agent systems (MASs) with consideration of input saturation under the self-triggered mechanism. In the context of discrete-time systems, a self-triggered strategy is developed to determine the time interval between the adjacent triggers. The triggering condition is designed by using the current sampled consensus error. Furthermore, the consensus control protocol is designed by means of a state feedback approach. It is shown that the considered multi-agent systems can reach consensus with the presented algorithm. Some sufficient conditions are proposed in the form of linear matrix inequalities (LMIs) to show the positively invariant property of the domain of attraction(DOA). Moreover, some sufficient conditions of controller synthesis are provided to enlarge the volume of the DOA and obtain the control gain matrix. A numerical example is simulated to demonstrate the effectiveness of the theoretical analysis results.

I. INTRODUCTION

IN recent years, the consensus problem has attracted increasing attention in the research of multi-agent systems (MASs)as it is the core problem in cooperative control, tracking control, formation control [1]-[8], etc. Most of the existing literature studied the consensus problem for the MASs which were described by single-integrator or double-integrator dynamical models [9]. However, due to the requirements of practical applications, it is of great interest to investigate the consensus problem for a class of MASs which can be formulated as general linear models [10].

Each agent in the MASs is controlled by a micro-controller in a practical scenario. It should be considered that each agent obtains the consensus error by measuring the information from its neighbors with limited communication and computational resources. In [1], motivated by the use of embedded micro-controllers with limited resources, the authors proposed an event-triggered control scheme based on the ratio between the measurement error and the sampled state. The event-driven control strategy has been considerably studied for its capability of reducing the consumption of computational resources and communication frequency which must be taken into account during controller design for the practical system. Many celebrated results on event-driven control have been developed, see for example, [11]-[16]. The authors in [17] exploited the event-triggered zero-order-hold(ZOH) in the framework of sliding mode control for stochastic systems. The event-triggered communication approach was adopted in [18] to optimize the utilization of communication resources. In [19], a self-triggered scheme was developed via model predictive control in the context of nonlinear systems.The triggering condition was designed by guaranteeing the objective function to be decaying.

Moreover, physical constraints are ubiquitous in practical systems, i.e., input saturation [20], output bounded [21], state constraint [22], etc. Thus, it should be taken into account in the controller design. Otherwise, it may lead to nonlinearities in the linear systems which will induce the performance degradation of closed-loop systems, and even loss of stability. Many efforts have been devoted to the theoretical analysis of saturation, see for example, [23]-[27]. In [28], the authors adopted a boundary control strategy in handling input nonlinearities and unknown external disturbances for a class of flexible riser systems. The authors of [29] utilized a radial-basis-function (RBF) neural network to approximate system uncertainties, with which the closed-loop system was shown to be semi-global uniformly ultimately bounded. However, most of existing literature took the continuous-time systems into consideration, while the discrete-time model should be studied when the microcontroller is adopted. In addition, event-driven control should be studied to reduce computational resources used in fulfilling the physical constraints. In recent decades, this has attracted tremendous attention, and several results have been presented.In [30], a distributed event-triggered control strategy was provided for global consensus of MASs which can be formulated as a linear system subject to input saturation. In [31],the authors investigated an output-based event-triggered control scheme for linear systems with actuator saturation. An anti-windup compensator and an event generator were designed to overcome saturation. The authors presented an eventtriggered controller in [32] taking the actuator saturation and anti-windup compensation into consideration. In [33], the authors studied the event-triggered control problem for a class of linear systems with actuator saturation and additive disturbances. Some sufficient conditions were given for synthesis of the proposed controller and event-triggered control problem to maximize the estimation of the domain of attraction(DOA). Many of the published works exploited the eventtriggered condition based on the relationship between state error and sampled state. In general, it should be checked according to the sampling interval in discrete-time systems in the context of an event-driven mechanism. However, a violation of the triggering condition may occur between adjacent sampling instants, which may lead to instability of the system in the presence of time delay. In [34], both event- and self-triggered transmission schemes were proposed for dynamic systems subject to actuator saturation. Distinct from the event-triggered mechanism, self-triggered control was proposed to determine the triggering interval between the adjacent triggers at each triggering instant. A self-triggered mechanism is of great interest for its use in saturated system controller design. It is worth noting that the triggering condition is obtained based on current sampled data without checking the states of the system at each sampling instant, which implies computational resources could be significantly reduced.

It should be mentioned that consensus problems for the MASs formulated by linear models are worth being studied in practice. In the discrete-time context, input saturation is taken into account in controller design. In addition, from a practical perspective, we adopt a self-triggered mechanism to reduce computational resources.

In this paper, a self-triggered consensus strategy is proposed for a class of general linear MASs subject to input saturation in the context of discrete-time dynamics. The main contributions of this paper are summarized in the following.

1) In this paper, we investigate the consensus problem for a class of linear multi-agent systems subject to input saturation,which is a common problem from the application perspective.It is worth noting that the consensus problem with consideration of input saturation for high-order linear MASs has not been fully studied in the context of event-driven control [35]. Inspired by the differential inclusion approach,the input saturation is taken into account in controller design to fulfill practical constraints.

2) Compared with the widely adopted event-triggered mechanism [3], [33], [36], a self-triggered mechanism is developed in this paper to reduce computational and communicational resources, which can determine the next triggering time instant without measuring the states until next trigger. The triggering condition is designed by using the current sampled states of the considered MASs.

3) A control protocol is developed for each agent in the MASs under study towards consensus. Some sufficient conditions are given in the form of linear matrix inequalities(LMIs) to guarantee the positively invariant property of the DOA. The theoretical analysis for input saturation is presented to enlarge the DOA under the proposed triggering condition.Furthermore, the control gain matrix in the consensus protocol is obtained in the controller synthesis design.

The rest of this paper is organized as follow: Section II presents some crucial preliminaries for the theoretical analysis and formulates the considered problem in this paper. Section III designs the self-triggered consensus strategy and gives the convex optimization problem to determine the time interval before the next trigger. Moreover, some sufficient conditions are proposed in LMIs form to maximize DOA under the proposed controller. Meanwhile, the gain matrix in the consensus protocol is obtained by the controller synthesis. The simulation results are given in Section IV to verify the effectiveness of the theoretical results. Section V concludes this paper.

II. PRELIMINARIES AND PROBLEM FORMULATION

To describe the considered consensus problem in this paper,we briefly recap some definitions on graph theory in this section. Thereafter, we formulate the self-triggered consensus problem for linear MASs. In addition, some crucial definitions and lemmas are given for controller design.

A. Notations

We adopt the following notations throughout this paper:The labels R and N represent the collection of real and integer numbers, respectively. The superscriptsnand + of Rnand N+depict the dimension of the matrix and the positive integer number set, respectively. For a given real matrixA,anddenote the maximum and minimum eigenvalues ofA,respectively.X⊗Yis the Kronecker product of the given matricesXandY. Given two real symmetric matricesA,Band a real matrixCwhose dimension is suitable toAandB,stands for a symmetric matrix, where the label * is the transpose of matrixC.Inrepresents the identity matrix with dimensionn. Denote the sign function as sign(x) where sign(x)=1 forx＞0 , sign(x)=-1 forx＜0 , andsign(x)=0 forx=0.

B. Graph Theory

C. Problem Formulation

Consider the MASs containingMhomogeneous agents.Each agent can be formulated as the following linear dynamical model subject to input saturation

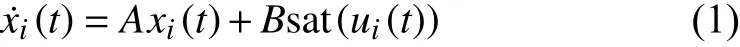
wherexi(t)∈Rnandui(t)∈Rmare the state and control vectors of agenti(i={1,2,...,M}), respectively.A∈Rn×nis the system matrix, andB∈Rn×mis the input matrix. The saturation function sat(ui(t))=[sat(ui1(t)),...,sat(uim(t))]Tand forl=1,2,...,m, we define

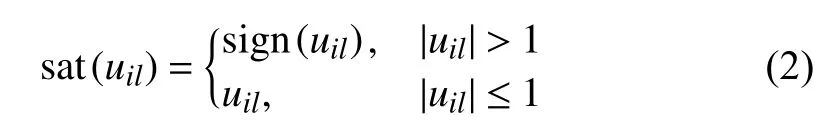
whereuilis thelt h element ofui.

Remark 1:It is worth mentioning that if linear systems are formulated by

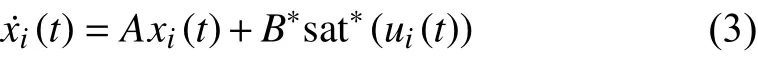
where

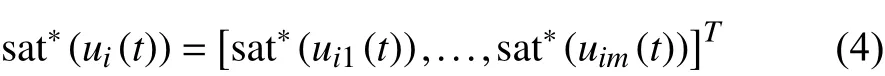
with arbitrary saturation value for each input signal, it can be transformed into form (1) whose input is bounded by 1. If the saturation on each control input is another value instead of 1,the saturation value on each input signal is expressed by,l={1,...,m}, and the saturation function sat*(uil(t)) has the similar form as (2).B*is defined assuch that the system (3) can be rewritten as

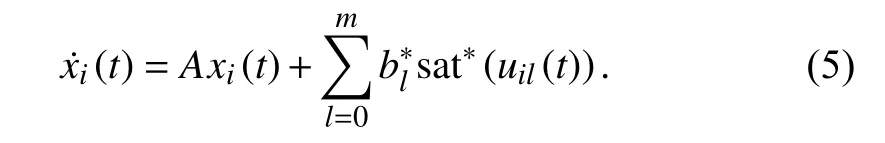
Then we can obtain the following system:

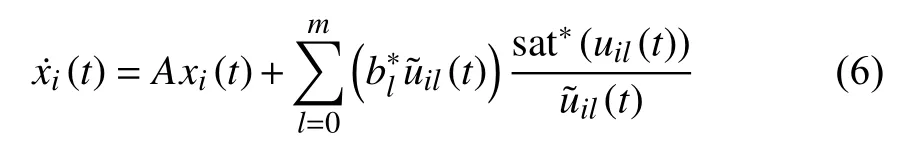
The closed-loop control system should be taken into account in the context of a discrete-time system according to the sampling controller, so that the system in (1) can be discretized [13]. Suppose the sampled interval beT(T＞0)and the sequence of sampling instants be {1,2,...,k,k+1,...}.The system in (1) can be rewritten as follows:

where

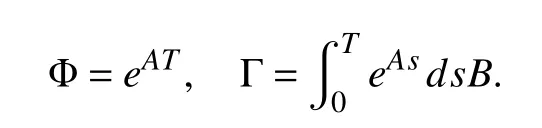
For the consensus problem of MASs, denote the consensus error in the following:

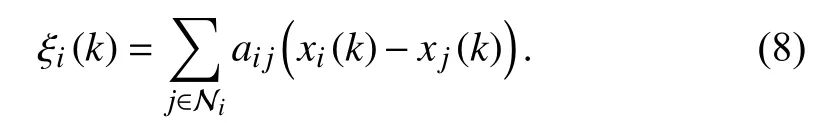
In this paper, the consensus protocolui(k) is designed as follows:

forwheredenotes the selftriggered instant,is the feedback gain matrix which will be designed in the subsequent section, andai jis the element in the adjacent matrix A corresponding to the undirected graphThe control input is updated based on the selftriggered strategy atkstand holds the same value before the next sampling instantkst+1.

Definition 1 [37]:The MASs with each agent formulated in(1) is said to be reaching a consensus, if

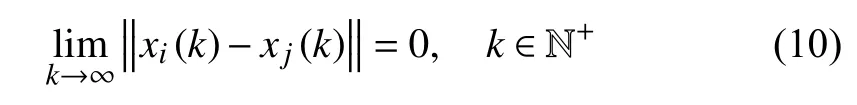
for any initial valuexi(0)∈ε(P,ρ), where the ellipsoid area ε(P,ρ)stands for

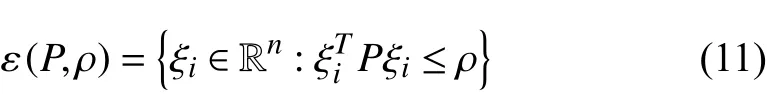
withPbeing a symmetric positive definite matrix and ρ being a positive scalar.

To tackle the input saturation in the controller design, the DOA is exploited. Some definitions and lemmas are given in the following for investigating the DOA of system (12).given asF∈Rm×n, whoseq- th row can be denoted asfq, so

Definition 2 [36]:In terms of the saturation, a matrix is that there is a symmetric polyhedron

Definition 3 [38]:A set χ is said to be invariant, if for all trajectories whose initial state ξ(0)∈χ, it holds that ξ(t)∈χ,∀t≥0.

Definition 4 [39]:For the initial statedenotes the state trajectory of the system. The DOA of the origin is

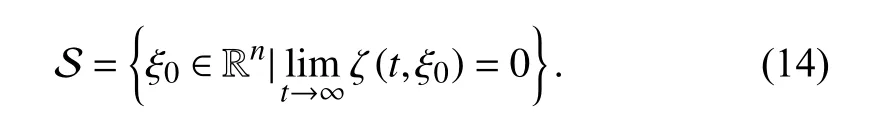
Definition 5 [40]:Let Υ be the set of all combinations ofm×mdiagonal matrices whose diagonal elements are either 1 or 0, so that there are 2mmatrices inEach of them can be denoted asEs, namely,Denoteand define

Moreover, some crucial lemmas are recapped as follows for the theoretical analysis in this paper.

Lemma 1 [41]:Let. Suppose ‖ φ‖∞≤1. Then

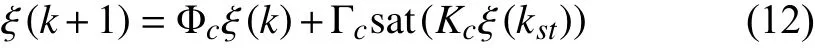
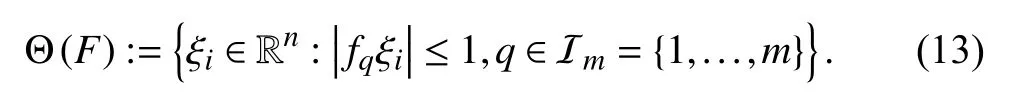
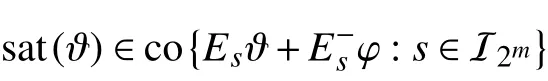
where c o(·) denotes the convex hull.

Lemma 2 [42]:For a given ellipsoid ε (P,ρ) and polyhedron Θ(F), there exists ε (P,ρ)⊂Θ(F), if

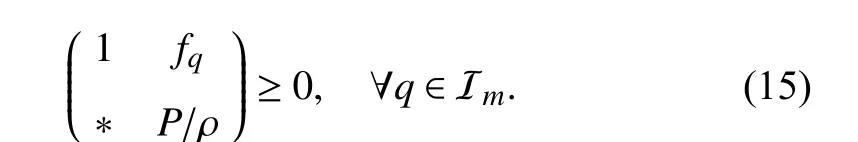
III. MAIN RESULTS

In this section, a self-triggered strategy is presented, and the triggering condition is given based on the sampled states.Meanwhile, a convex optimization problem is constructed for determining the time interval before next trigger according to the triggering condition. Thereafter, we propose a method to design the feedback gain to stabilize the system in (12), which implies that the MASs can be guaranteed to reach consensus within the maximum triggered interval.

A. Self-Triggered Strategy

For the closed-loop system in (12), define the consensus error between two adjacent sampling instants by the following form:

where ξ(k) is the current consensus error at time instantk＞kst, and ξ(kst),st∈N+is the sampled one at the latest sampling instant. Thus, the self-triggered condition is designed as follows:

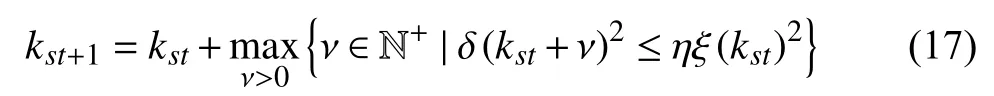
where δ (kst+ν) is the measurement error at the sampling timekst+1=kst+ν, ν is the inter-sampling periods between two adjacent triggers, and η ＞0 is a user-defined scalar.

Fork∈[kst,kst+1), we can get

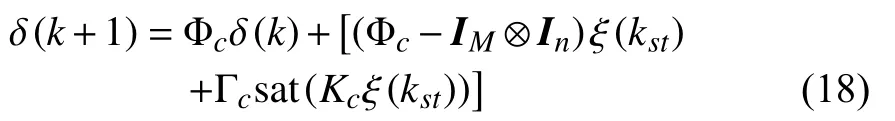
with δ(kst)=0 . According to the definition of state error δ(k)in (16), one can get the following expression:

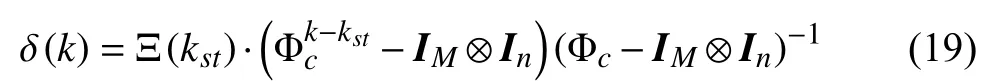
where

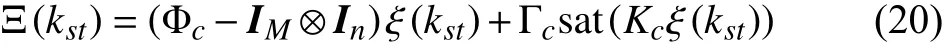
is a constant matrix. Thereafter, one can get

where

Thus, the self-triggered condition in (17) can be rewritten as follows:

Remark 2:It is worth to mention that (23) is equivalent to

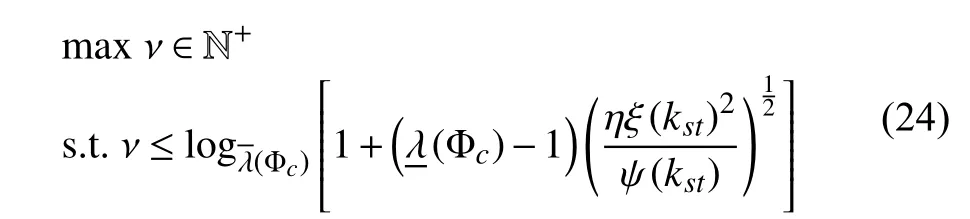
where ν ∈N+gives the lower bound on the time interval before next trigger. Compared with (23), (24) can be solved without a convex optimization solver, which implies that the computational burden can be reduced. Moreover, the optimization objective ν ∈N+is introduced to avoid zeno behavior.

B. Controller Parameter Design

From the above, a self-triggered condition is proposed to design a state feedback controller for the closed-loop system subject to bounded inputs. One problem is to show that the given ellipsoid is positively invariant and the other is to find the DOA based on the given positively invariant set. From the definition of DOA and positively invariant set, the DOA has the largest volume if ρ is maximum in the positively invariant set ε(P,ρ). It should be clarified that, in this paper, the saturation is assumed to be 1 constantly, which means ρ=1.Therefore, an appropriatePis designed in the following to enlarge the volume of DOA. We propose two theorems to summarize the theoretical analysis results as follows.

Theorem 1:Given a state feedback control gain matrixKand a positive scalar η, the ellipsoid ε(P,ρ) is a positively invariant set for the closed-loop system (12), if the following condition is satisfied:

Proof:In accordance with Definition 3 on a positively invariant set, define the Lyapunov function in a quadratic form as follows:

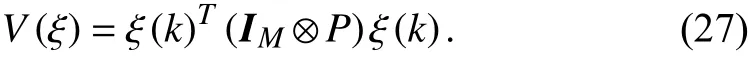
The difference ofV(ξ) along the trajectory of system (12)is denoted as

which should satisfy

where

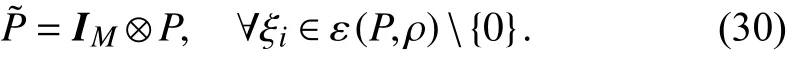
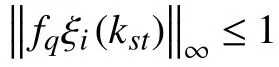
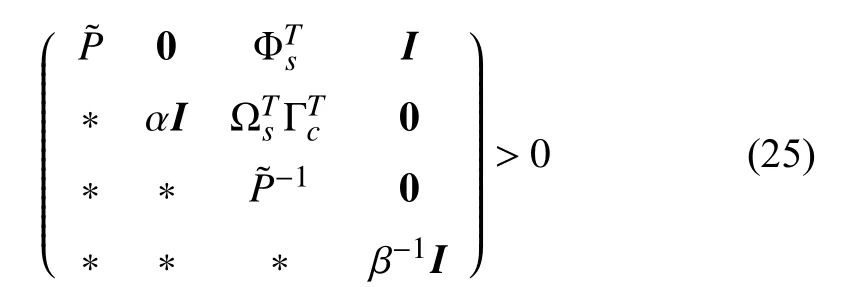
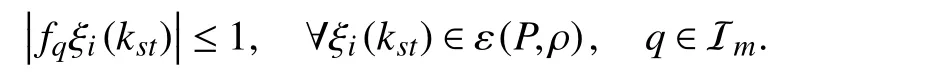
In light of Lemma 1, one can have

Therefore, inspired by the closed-loop system in (12), the following expression can be deduced

where

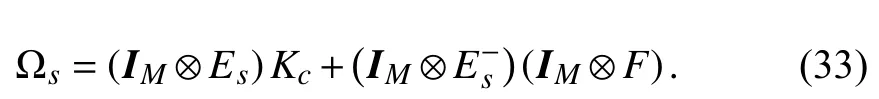
Then we can obtain

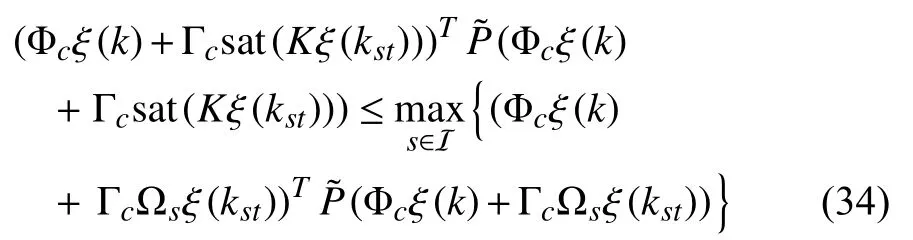
according to the property of a convex hull. To prove (29), it is sufficient to prove that

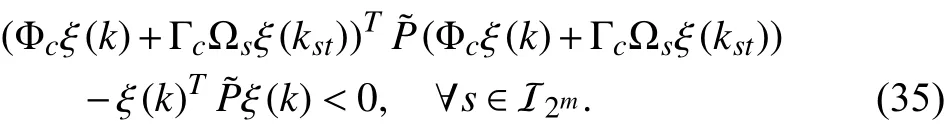
As the consensus error in this paper defined in (16) is satisfied when it triggers, (35) can be rewritten in the following form:

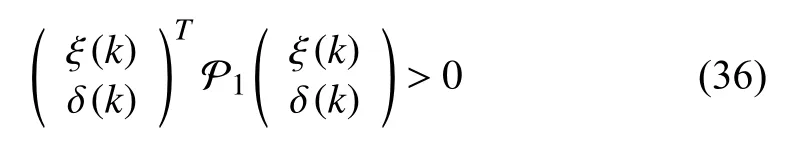
with

by letting

and

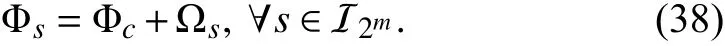
In terms of the self-triggered condition designed in (17), we have

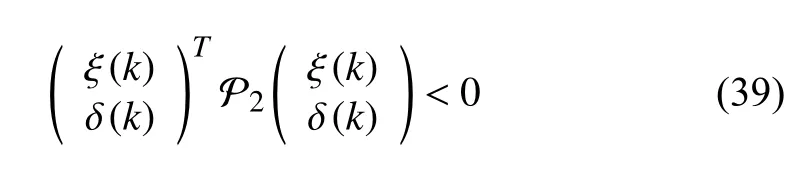
with

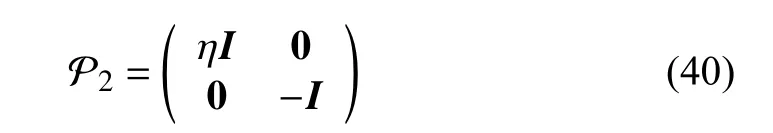
whereIand 0 are the identity and zero matrices with appropriate dimension, respectively. Introducing a given positive scalar α, we can obtain the following inequality by combining (36) and (39) using S-procedure.

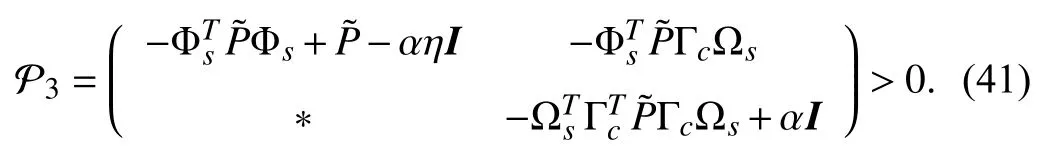
Thus, (41) can be rewritten as follows via Schur’s complement.

Letting β =αη, (25) can be obtained.

In what follows, one problem is determining how to enlarge the volume of DOA by designing an appropriateP; the other is determining how to derive the corresponding controller gainK. We explain the theoretical analysis results by the following theorem.

Theorem 2:The volume of the ellipsoid mentioned in Theorem 1 can be maximized by solving the LMIs optimization problem as follows:

where

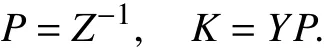
Proof:In light of (25), by pre- and post-multiplying a diagonal matrixone can have

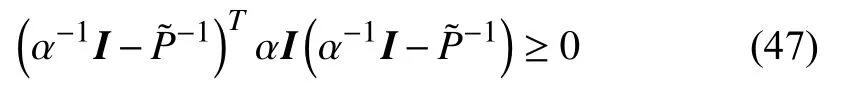
which is equivalent to

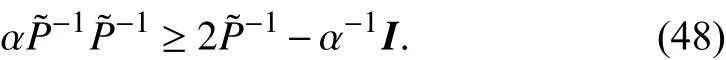
Thus, (46) can be rewritten as follows:

where

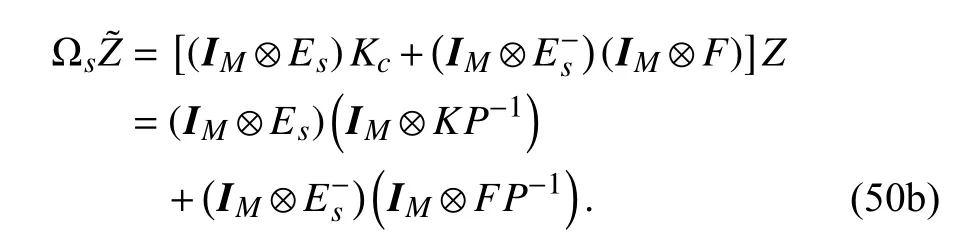
LettingY=KP-1andW=FP-1, (43) can be obtained.Furthermore, by pre-/post-multiplying a diagonal matrix diag{I,P-1}, (26) can be rewritten as (44).

Remark 3:It is worth pointing out that we should maximize ρto enlarge the volume of ε(P,ρ) but it is assumed to be 1 in this paper. The alternative way is to minimizeP. The CVX toolbox in MATLAB can solve the LMIs optimization problem directly. A function logdet(Z) is introduced to solve the so-called determinant maximization problem, such that the minimumcan be obtained.

C. Algorithm Description

According to the proposed self-triggered consensus approach, Algorithm 1 is described as follows to demonstrate the procedure.

Algorithm 1 self-triggered consensus for mass with input saturation

Remark 4:It is worth to mention that, for a given practical system, the sampling intervalTis determined by the bandwidth of the sensors and the micro-controller. Moreover,the user-defined η in the triggering condition (23) is a triggering level parameter, which implies the triggering interval gets larger as η grows, and vise verse. In addition,another user-defined parameter α is introduced in Sprocedure, which represents the trade-off level between (37)and (40).

IV. SIMULATIONS

In this section, a numerical example is given to demonstrate the effectiveness of the theoretical analysis results.

Consider the MASs containing five agents. Each agent in the considered MASs can be described in the following dynamical model:

The communication topology is shown in Fig. 1 . The adjacent matrix can be obtained according to the communication graph in which the weight of each edge is assumed to be 1. Thereafter, we can get the corresponding Laplacian matrix.

Fig. 1. Topology of the considered MAS.

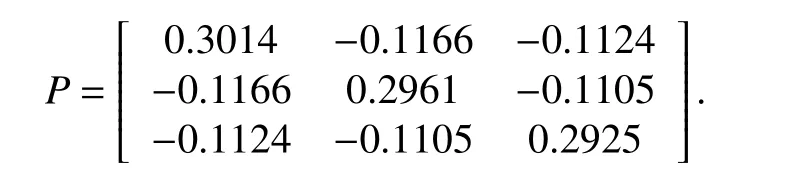
The simulation is conducted by following Algorithm 1, and the results are reported in Figs. 2-6. It is seen in Figs. 2-4 that the consensus errors of each state converge to zero as time trends to infinity, which implies the considered MASs can reach consensus with the presented control protocol under the self-triggered mechanism. To demonstrate that the input saturation can be guaranteed, Fig. 5 gives the control input signals of each agent. It is shown that the input saturation of each agent is fulfilled during the simulation time horizon.Moreover, to reveal the effectiveness of the self-triggered mechanism, the triggering instants are plotted in Fig. 6. It is worth noting that the triggering count is significantly reduced according to Fig. 6. It is observed that the proposed selftriggered scheme can render the MASs to reach consensus with the triggered interval determined at each self-triggered instant.

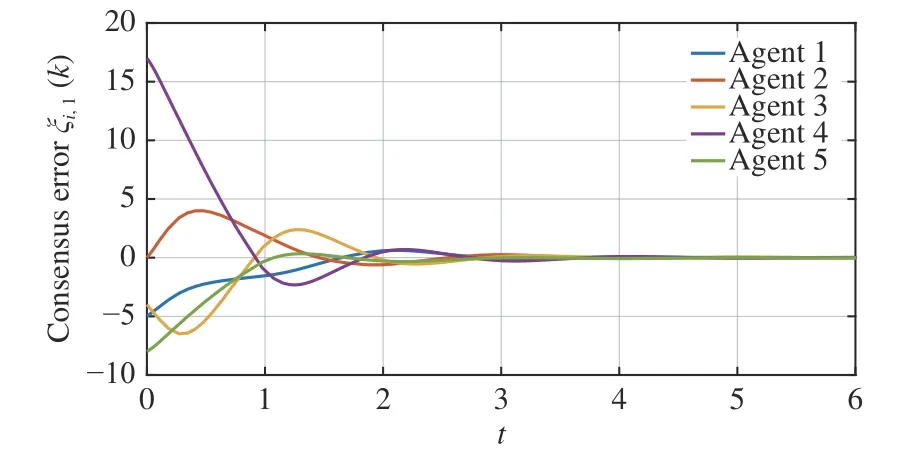
Fig. 2. Consensus error on ξ i,1(k) of each agent.

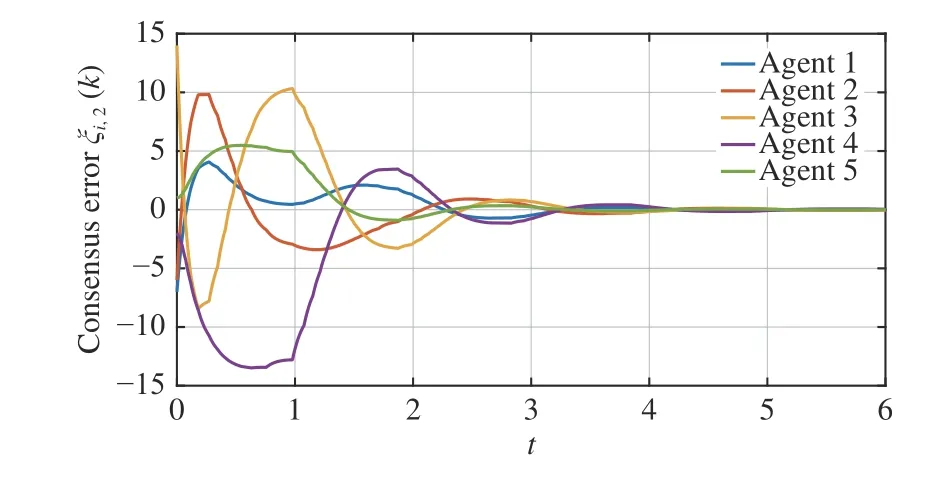
Fig. 3. Consensus error on ξ i,2(k) of each agent.

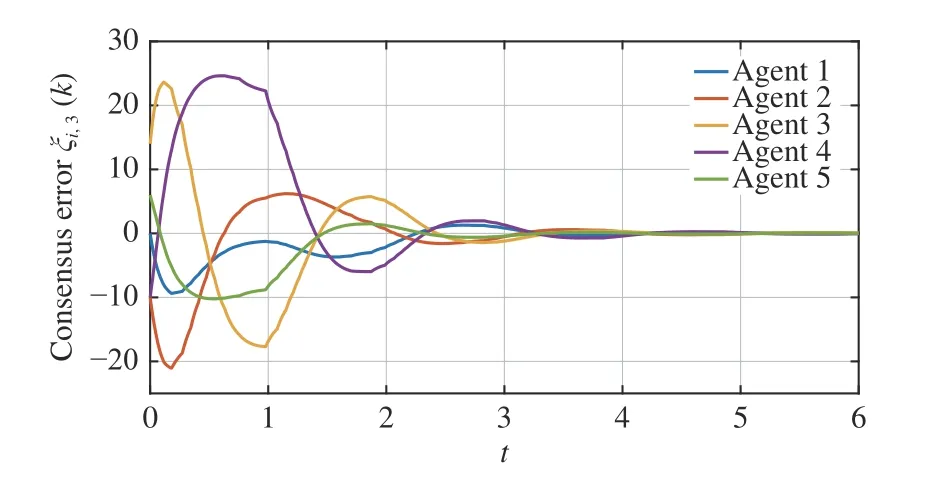
Fig. 4. Consensus error on ξ i,3(k) of each agent.

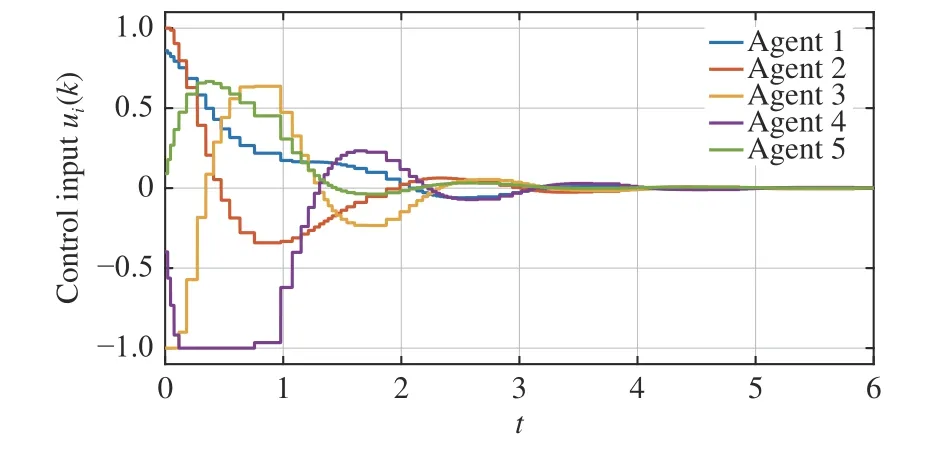
Fig. 5. Control input of each agent.

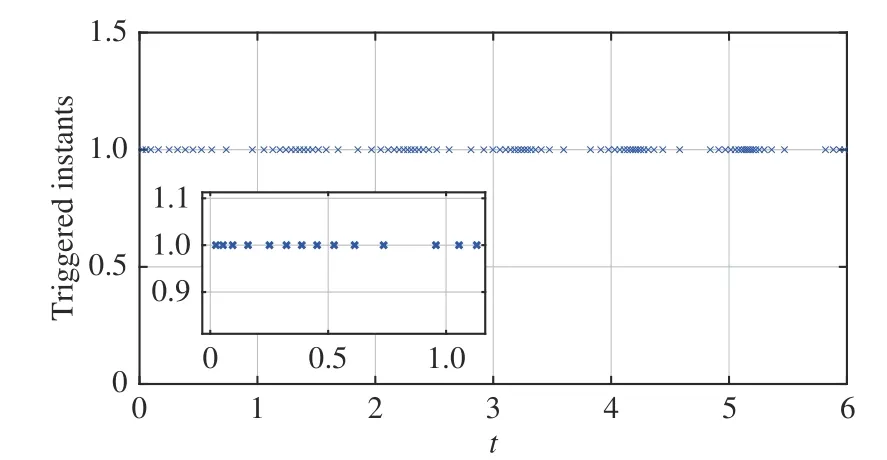
Fig. 6. Self-triggered instants (The blue crosses represent the triggering instants).

V. CONCLUSION

In this paper, a self-triggered consensus scheme is proposed and the controller synthesis approach is discussed for linear multi-agent systems subject to input saturation. Based on the changing rate of consensus error, the self-triggered strategy is exploited to reduce the communication burden. To find the maximum positively invariant ellipsoid with consideration of the input saturation, a sufficient condition is given in the form of LMIs. Thereafter, the feedback control gain of the presented self-triggered controller can be obtained. Moreover,a numerical example is given to verify the theoretical analysis results. The contribution of this paper is to present a selftriggered scheme which can handle the consensus problem of linear multi-agent systems with a digital micro-controller where the input signal is bounded with maximizing the DOA of the closed-loop multi-agent systems. Implementing the proposed algorithm in a practical system will be the subject of future works.