广东省中山市濠头中学(528437) 闫 伟

1.试题呈现与分析

例1(2019年清华大学自主招生考试第8 题)已知椭圆，过点F(2,0)的直线与椭圆交于A,B两点，点C在直线x= 3 上，若∆ABC为等边三角形，求∆ABC的面积．

试题分析题目结构清晰，以椭圆为背景，主要考查椭圆的焦点弦、几何性质、直线与椭圆的位置关系，三角形的面积等知识以及转化与化归、数形结合等数学思想，突出考查学生逻辑推理、推理论证及运算求解等方面的能力，试题的思维过程和运算过程体现了能力立意的命题思想，较好地体现了对直线与圆锥曲线的核心内容和基本思想方法的考查，亦较好地检测学生的数学素养和学习潜能.

2.解法探究

解法1(通性通法，少思多算)设直线l:x=my+ 2,A(x1,y1),B(x2,y2)，AB中点为N，联立整理可得(m2+3)y2+4my-2=0,

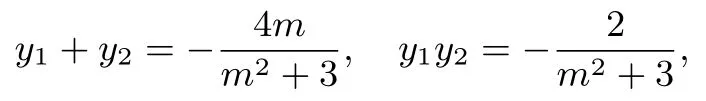
易求得N点横坐标

因为∆ABC为等边三角形，所以CN ⊥AB，即kCN=-m，于是

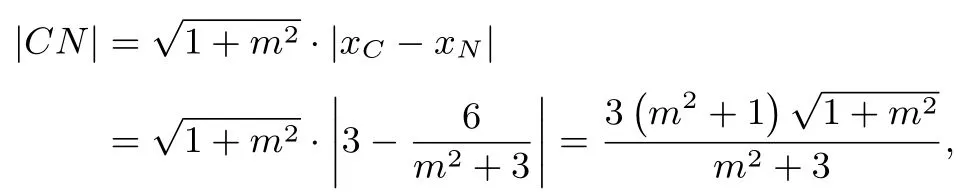
评注本解法通过设直线方程并联立直线与椭圆结合韦达定理，再利用坐标表示弦长建立关于斜率的等式达到求解参数的目的，解题思路清晰，学生容易想到，但是运算较为繁琐，要求学生提高数学运算能力.下面先给出两个结论：

(1)设AB是过椭圆= 1 (a ＞ b ＞0)右焦点F的弦，直线AB与x正半轴所成的角为θ，则

(2)设椭圆焦点弦AB的中垂线交长轴于点D，则e为椭圆的离心率.

图1

证明(1)如图1所示： 过A点作直线的垂线于A1，由椭圆的第二定义知即化简整理得同理得

(2)如图1知

解法2(巧用结论，多思少算)设直线AB与x正半轴所成的角为θ，由题意知离心率根据上述结论正三角形的边长|AB|=过A,B分别作直线x= 3的垂线，垂足分别为A1,B1如图2所示，由椭圆第二定义得|FA|=|A1A| · e,|FB|=|B1B| · e,设∠CBB1=α,∠CAA1=β，显然α+β=60°，在Rt∆BCB1中

所以

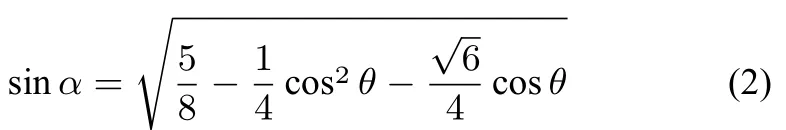
在Rt∆ACA1中，同理可得因 为cosβ= cos(60° -α)=结合(1)(2)得于是故∆ABC的面积

评注注意到直线AB过焦点，故可借用焦点弦结论，利用直线倾斜角表示弦长，进而通过图中角度关系β+α=60°建立三角恒等式求解参数θ，思路相对简洁，计算量较解法1大大减少.

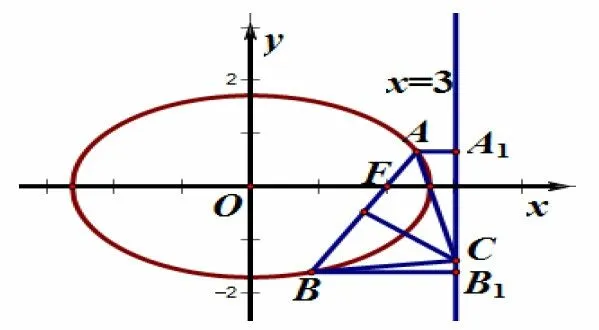
图2

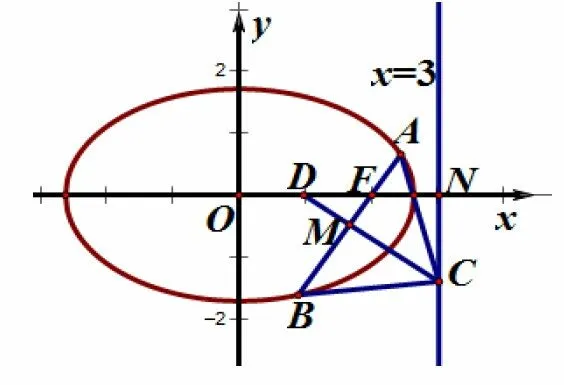
图3

解法3(大道至简，深思妙算)设直线AB与x正半轴所成的角为θ，由上述结论可知

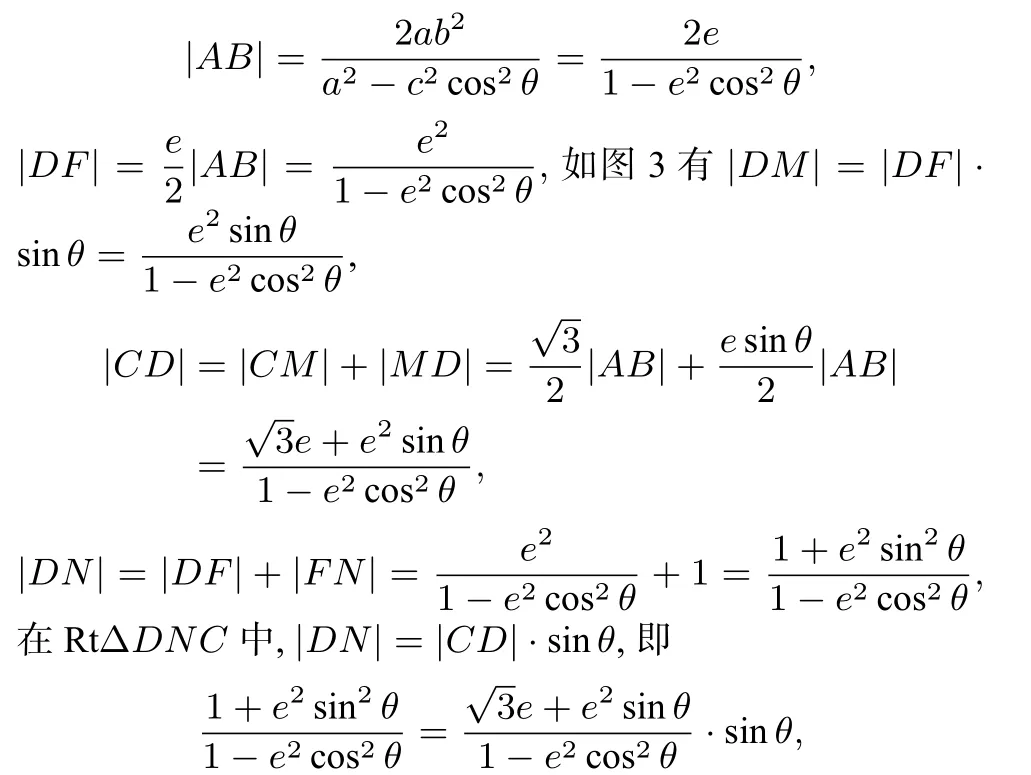
评注考虑到直线AB过焦点而且以线段AB为边的正三角形出现，很自然的联想到焦点弦的中垂线性质，直接利用直角三角形中几何关系建立角度参数的等式，容易操作，达到化繁为简的效果;体现了解题中尤其是解决小题时二级结论的优越性.

3 应用拓展

3.1 解法3 的应用

解法3 巧妙的借助焦半径及焦点弦的中垂线性质，极大地减少运算和推理论证过程;焦点弦的中垂线结论对于解决垂直于焦点弦一类问题有着相当的优势，相比传统的以直线的斜率作为参数，再联立直线和曲线得到一个一元二次方程，然后利用韦达定理求解，这样往往运算量特别大，而选择角度形式的焦点弦则可大大简化计算，直达问题结论，收到事半功倍的效果;下面对上述结论的精彩应用做些拓展.

例2过抛物线x2= 4y的焦点F的直线交抛物线于A,B两点，点C在直线y=-1 上，若∆ABC为等边三角形，则该三角形的边长为.

图4

解析类比椭圆结论易证抛物线的焦点弦|AB|=设焦点弦AB的中垂线交对称轴于点D，则如图4作AB的中垂线交y轴于D点，AB中点M，设AB与y轴夹角为θ，则根据已知结论因为|MD|=|DF|·且又因为|DC|=|MD|+|MC|，代入并整理得所以|AB|=12.

评注本题借用焦点弦的角度形式表示弦长，再根据焦点弦的中垂线结论及题中几何关系得到关于sinθ的等式，从而快速准确求出sinθ，解题运算量少，过程简洁，体现了小题小做妙用二级结论的优点.

例3已知椭圆的焦点在x轴上，一个顶点为(0,1)，离心率，过椭圆右焦点F的直线l与坐标轴不垂直，且交椭圆于A,B两点.

(1)求椭圆的标准方程; (2)M(m,0)是线段OF上一个动点，且求m的取值范围.

解析(1)椭圆标准方程为过程从略;

故m=c-|MF|=2-

评注解题的关键在于判断M点的位置，进而借助焦点弦中垂线结论利用焦点弦的角度形式表示m，再根据三角函数的有界性求解;相比用直线的斜率表示参数m，然后联立方程结合韦达定理求解，本题解法简便高效，可谓是“小结论，大用途”.

例4如图在平面直角坐标系中，已知椭圆1 (a ＞b ＞0)的离心率为且右焦点F到左准线l的距离为3.

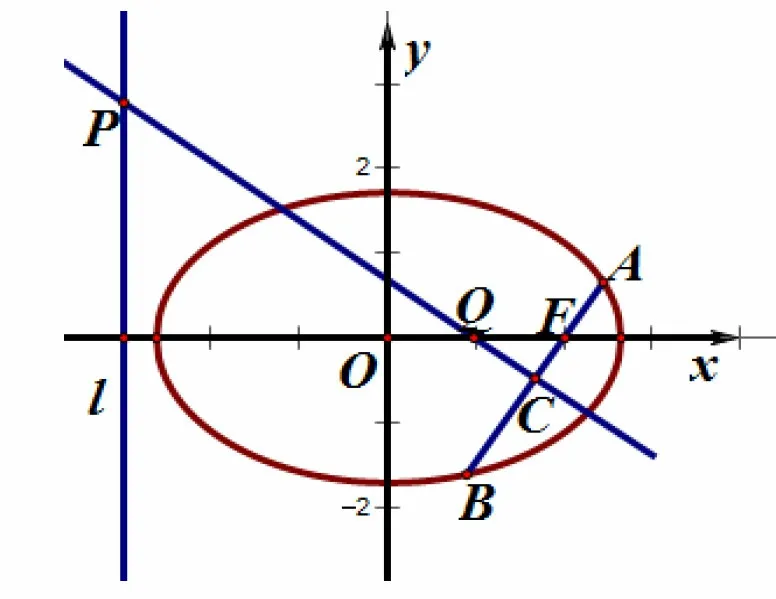
图5

(1)求椭圆的标准方程;(2)过F点的直线与椭圆交于A,B，线段AB的垂直平分线分别交直线l和AB于点P,C，若|PC|= 2|AB|，求直线AB的方程.

解析(1)易求得椭圆方程为

(2)如图5所示，设直线AB与x正半轴所成的角为θ，则

设PC交x轴于点Q，则

又因为

结合(1)(2)可得sinθ=故直线AB的方程为x±y-1=0.

评注解题中利用焦半径的角度形式表示弦长，再根据图中几何关系及焦点弦的中垂线结论建立直线倾斜角的等式，极大的简化计算和推理论证过程，具有直观、简捷的特点，平常教学中解答解几试题应重视二级结论的积累，能快速有效的锁定问题结论.

3.2 试题结论的拓展

一道好的试题的研究价值不应仅仅停留在解法及应用上，还应该对试题本身做深入的研究.由解法2 和3 可知直线AB的方程是确定的为x±y-2=0，那么很自然的联想到更一般的情形：

拓展1已知过椭圆=1(a ＞b ＞0)右焦点F的直线l交椭圆于A,B两点，作线段AB的垂直平分线交直线于C点，若∆ABC为等边三角形，则直线l的方程为

拓展2已知椭圆=1(a ＞b ＞0)，过椭圆长轴上一点P(t,0)(t ∈(0,a))的直线l交椭圆于A,B两点，作线段AB的垂直平分线交直线于C点，若∆ABC为等边三角形，则直线l的方程为

证明设直线l:x=my+t，A(x1,y1),联立并整理得：

设AB中点M(xM,yM)，则于是

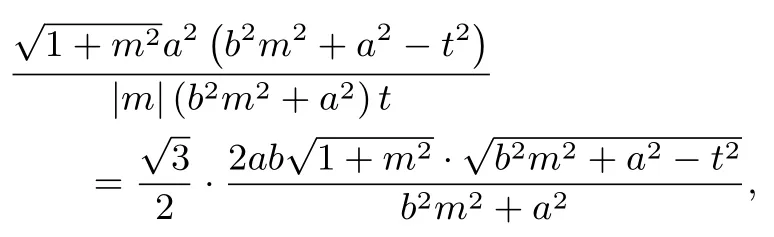
拓展1 是拓展2 的特殊情形，只需令t=c即可.

4 结束语

数学家波利亚曾说过：“掌握数学就意味着善于解题”[1].引导学生学会解题是数学新课标教学的重要组成部分，数学问题的解决仅仅是一个开端，更重要的是解题后的反思与回顾.遇到一道经典题目，不能仅仅停留在会解的层面，还应反思题目是否有其他解法? 解法能否推广? 能否将试题进行拓展? 试题的本质是什么? 唯此才能将试题探究的价值最大化，从而更好的引导教学.