载人探月飞行器跳跃再入轨迹优化问题研究

2020-02-01刘旭，李爽*，曹涛，宋婷

载人航天 2020年6期

刘旭，李爽*，曹涛，宋婷

(1.南京航空航天大学航天学院，南京 210016; 2. 上海航天控制技术研究所，上海 201109)

1 引言

中国载人航天工程已经掌握近地轨道载人飞行器的返回与回收技术[1]，随着嫦娥三号和嫦娥四号分别在月球正面和背面成功着陆[2-3]，载人探月工程已经成为中国航天未来发展方向之一。

相比近地轨道再入返回，载人探月飞行器的返回轨迹往往是偏心率较大的椭圆轨道或者双曲线轨道，因此再入速度较大，接近第二宇宙速度。若沿用近地再入任务的直接弹道再入方式，热流和过载峰值都将超过飞行器和航天员所能承受的极限。此外，受测控能力限制，且着陆场的选取约束要求陆地定点着陆，因而采用跳跃式再入是目前较为理想的月地高速再入方案[4]。跳跃再入轨迹一般划分为初次再入段、跃升段、开普勒段、二次再入段和着陆段。再入过程中飞行器采用配平迎角飞行，通过升阻比控制或倾侧角控制实现再入轨迹调整，从而对过载、热流、落点散布等指标进行控制[5]，因此飞行器的升阻比和倾侧角控制能力直接决定了落点的可调整范围和精度。

典型的跳跃再入飞行器包括美国的Apollo飞船和猎户座飞船[6-8]以及中国探月工程三期再入返回试验器(CE-5T1)[9]。其中，Apollo飞船第一次进入大气层的速度在10.7 km/s，升力控制跃起高度为80 km左右，具有2200～4600 km的航程机动的能力，侧向航程修正能力优于370 km，再入最大过载处于4～7g0，落点精度约为50 km；猎户座飞船外形与Apollo飞船类似，升阻比约为0.25～0.27，全程采用反作用控制系统(Reaction Control System, RCS)模式控制跳跃式再入返回，但其搭载的新一代人-机协同控制策略可以让返回舱轨道平面可调，不再需要将着陆场设置在航天器轨道平面内，而且采用了精度更高的制导控制算法，再入段的峰值过载、热流情况较阿波罗飞船均有较大改善，落点控制精度可达到5 km内；CE-5T1的预期再入航程介于5600～7100 km 之间，实际航程超过6000 km[9]。

跳跃再入轨迹规划本质上是复杂的多约束、非线性最优控制问题，常用的求解方法包括间接法和直接法。间接法基于拉格朗日乘子法和庞特里亚金极值原理，将多约束最优控制问题转化为多点边值问题，然后采用优化算法求解边值问题获得最优解。早期Shi[10]基于Chapman方程和匹配渐近展开法，分别求解了二维和三维场景下的无约束大气进入轨迹，但仅能得到精度有限的一阶近似解；随后，Kuo等[11]引入修正的查普曼(Chapman)变量，采用改进的匹配渐近展开法获得了地球大气进入轨迹的一阶和二阶近似解；近来，吴旭忠等[12]基于间接法提出一种结合自动判断约束结构和初始化对应打靶方程技术的同伦方法，增大了跳跃式再入轨迹优化问题的收敛半径。然而数值优化算法对协态变量初值非常敏感，同时协态变量没有明确的物理意义，其初值难以猜测，导致间接法算法收敛性较差。同时，间接法还存在必须推导一阶最优条件、收敛半径小、路径约束问题中控制切换结构难以预知的缺点[13]，因此应用间接法进行跳跃式再入轨迹优化具有明显的局限性。

相比之下，直接法不需要推导一阶最优条件，适用于多段、多约束轨迹优化问题，且不需要猜测协态变量初值，对状态变量初值也不敏感，具有良好的通用性和收敛性[13]。直接法中的局部配点法是一种通用性较强的轨迹优化方法，通过在一组离散节点上对最优控制问题进行离散，将轨迹优化问题转化为非线性规划(Nonlinear Programming, NLP)问题，并采用序列二次规划(Sequential Quadratic Programming, SQP)算法进行求解[14-15]。局部配点法在国外已经到得到广泛的应用，轨迹优化软件OTIS[16]就是基于局部配点法开发的。

本文采用基于稀疏差分[17-18]和多分辨率技术的改进局部配点法[19-21]开展载人高速再入总体方案研究，通过求解定点着陆问题、落点区域问题、再入参数敏感度问题和轨迹重规划问题的最优再入轨迹，论证载人飞行器在不同工况下的可行再入方案，确定再入轨迹对各项再入参数的敏感程度，为后续载人高速再入任务提供参考。

2 再入问题描述

2.1 动力学模型

对于再入轨迹优化问题，一般遵循非旋转均质地球假设，且可忽略地球自转影响，此时描述大气再入飞行器质心运动的微分方程为式(1)～式(6)：

(1)

(2)

(3)

(4)

(5)

(6)

其中，r为地心到飞行器质心的径向距离，V为飞行器的速度值，θ为经度，φ为纬度，γ为航迹倾角，ψ为航迹偏角(指向正东方向为0°，逆时针为正)，σ为倾侧角，地球引力g=μ/r2，m为飞行器的质量，L和D分别为升力和阻力，表达式如式(7)所示：

L=ρV2SCL/2,D=ρV2SCD/2

(7)

其中，CL和CD分别为升力系数和阻力系数，S为航天器的参考面积。ρ为大气密度，表达式如式(8)所示：

ρ=ρ0e-h/H

(8)

其中，ρ0为天体表面大气密度，h为飞行器高度，H为大气模型的参考高度。

2.2 约束条件

飞行器再入过程中应当满足式(9)～式(11)给定的热流密度、动压和法向过载约束：

(9)

(10)

(11)

飞行器二次再入段的初、末状态应当满足给定的边界条件，且飞行过程中各状态量均不能超过一定范围，定义状态的初、末约束E和过程约束C如式(12)所示：

E:x(t0)=x0,x(tf)=xf;C:xmin≤x≤xmax

(12)

其中，状态量x=[r,θ,φ,V,γ,ψ]T，x0和xf表示给定的初始和末端状态，xmin和xmax表示各状态量的的下限与上限。飞行任务一般要求满足全部初始约束，末端状态满足部分即可，例如定点再入时满足末端状态高度、速度和经纬度约束即可，末端航迹倾角和航迹偏角不做具体要求。

再入过程中控制量为倾侧角，σ的大小和变化速率均有一定变化范围，定义控制约束如式(13)所示：

(13)

若给定相应的目标函数J=M+L(M为终端项，L为积分项)，则载人多约束跳跃再入轨迹优化问题可描述为：确定控制量倾侧角σ，使得目标函数最小化，并满足动力学方程式(1)～(6)和约束条件式(9)～(13)。

3 改进的局部配点法

为了提高局部配点法的鲁棒性和优化效率，本文采用稀疏差分和基于广义二分网格的多分辨率技术，从NLP的稀疏性和离散节点数量两方面提高计算效率和精度。稀疏差分法采用原始轨迹优化问题的一阶偏导数表示NLP的一阶偏导数，构建稀疏偏导数矩阵，从而可以显著减小计算量[18]；多分辨率方法基于新型广义二分网格技术对离散网格节点进行调整，能以少量节点高精度地描述最优控制变量，从而减小轨迹优化的规模和计算时间[19]。本文改进局部配点法的流程如图1所示，在传统配点法的基础上，采用了稀疏差分技术进行偏导数计算，同时利用多分辨率技术进行网格细化，从而在保证算法精度的同时减小计算量。

图1 改进局部配点法的算法流程图Fig.1 Flowchart of modified local collocation method

3.1 稀疏差分

轨迹优化问题中，状态量x、过程约束C和目标函数J中积分项L都定义在整个时域区间，因而可以将这3项对自变量的偏导数定义在一起，如式(14)所示：

(14)

其中，G1的每一项仍为矩阵，以∂f/∂xT为例，如式(15)所示：

(15)

通常情况下，G1是稀疏矩阵。为了描述G1的稀疏型，定义struct函数如式(16)、(17)所示：

(16)

记：

S1=struct(G1)

(17)

式中，struct(G1)表示对G1的每个元素进行struct运算。S1表示G1的稀疏型。为了得到S1，不需要计算G1的每个元素的具体值，只需要判断是否为0。

类似地，可以定义边界约束E和目标函数J中Mayer项M对自变量的依赖关系矩阵和稀疏型如式(18)、(19)所示：

(18)

S1=struct(G1)

(19)

上述离散格式将同一个节点处的变量或约束记为一个列向量，这种记法与数值积分格式的形式一致，但是不利于推导偏导数矩阵的稀疏特性。为此，本文定义一种新的变量记法，将变量或约束的同一个分量在不同节点的值记为一个新的向量。以状态方程离散残差ξ为例，见式(20)：

ξ:,j=(ξ0,j,ξ1,j,…,ξN-1,j)T,(j=1,2,…,6)

(20)

利用这种新的变量记法，可将离散化的NLP问题重新描述为求解优化变量z，使得目标函数J(z)最小化，并且满足约束条件如式(21)所示：

Fmin≤F(z)≤Fmax

(21)

式中，优化变量z和约束函数F(z)的定义如下式(22)所示:

(22)

其中，t0，tf和Δt=tf-t0分别为轨迹优化初始时刻、末端时刻和优化时间。

3.2 广义二分网格

传统二进网格的初始节点数目必须是2j+1(j为非负整数)，使用不方便。为此，本文引入一种广义二分网格。

在区间[0, 1]内，由N个均匀分布的初始子区间对分得到的二分网格为式(23)：

(23)

式中，整数j表示网格分辨率，整数k表示节点位置，整数Jmax表示最高分辨率。由于j的最小值为-1，因而N必须为偶数。采用Wj, N表示属于Vj+1,N但不属于Vj, N的网格节点，即

(24)

因此，τj+1, k∈Vj+1, N满足如式(25)所示关系:

(25)

二分网格的子空间Vj, N满足嵌套关系，即V0,N⊂V1,N⊂…⊂VJmax,N，并且当Jmax→∞时，VJmax,N=[0, 1]。子空间Wj, N满足Wj, N∩Wl, N=∅ (j≠l)。由定义式(23)和(25)可知，二分网格是将区间[0, 1]不断细分获得，并且当k≥j时满足Wk,N∩Vj,N=∅。

3.3 网格细化

网格细化采用基本无振荡(Essentially Non-Oscillatory, ENO)插值算法离散节点插值，得到NLP问题的插值解，并根据插值解的变化率增删节点。本文采用牛顿插值法构造ENO插值，假设当前插值节点为τi,τi+1, …,τi+n，则新增加节点τnew的选取方式如式(26)所示：

(26)

其中，f为待插值函数，对应本文的动力学公式(1)～(6)，f(τi-1,…,τi+n-1)和f(τi+1,…,τi+n+1)表示f的差商，定义如式(27)所示：

(27)

在进行多分辨率优化之前，结合轨迹优化问题的精度要求，选取初始节点参数N，网格细化误差ε，最高分辨率Jmax，最大迭代次数Imax(Imax≥Jmax/2)。采用四阶Runge-Kutta法将轨迹优化问题转化NLP。设置I=1，Gold=V0, N，估计NLP优化变量初值，将其记为Xold。那么，改进的多分辨率方法的流程如下：

1)以Gold为初始网格、Xold为初值求解NLP。

2)网格细化方法如下(步骤①～④)：

①令Φold={uj,k:τj,k∈Gold}，并将其改写为

Φold={φl(τj,k):l=1,…,m,τj,k∈Gold}。

②初始化中间网格Gint=V0, N, 以及相应的函数Φint={φl(τ0,k)∈Φold, 0 ≤k≤N,l=1, 2, …,m}, 设j=-1。

③细化算法。

④本次细化得到的非均匀网格为Gnew=Gint, 相应的函数值Φnew=Φint。

3)置I=I+1。如果细化后网格保持不变，那么结束细化；否则，将步骤1)解出的NLP最优解插值到新网格Gnew，并以此作为新的优化初值Xold, 令Gold=Gnew, 返回步骤1)，继续细化。

以上细化算法是关键，具体如下：

1)求Wj,N和Gold的交集。

2)设置i=1，执行如下步骤(①～⑥)。

⑤将新增加节点对应的函数值添加到Φint。若新增节点对应的函数值未知，则利用Gold和Φold通过p阶ENO插值计算。

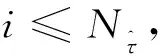
3)将j增加1。若j≤Jmax，返回步骤1)，否则转入下一步。

4)结束细化算法。

4 再入轨迹优化

载人探月飞行器再入时刻的各项参数取值如下：飞行器质量m为6800 kg，参考面积S为12.88 m2，升力系数CL和阻力系数CD分别为0.3892和1.3479，kQ为1.9027×10-4，地球海平面大气密度ρ0为1.225 kg/m3，参考高度H为7200 m，地球引力系数为3.986×1014m3/s2，地球半径取6378 km，地球表面重力加速度g0取9.81 m/s2，其余飞行器系统参数和再入条件如表1所示，其中初次再入段和二次再入段的法向过载峰值分别为6倍g0和4倍g0。

表 1 数值仿真参数

此外，改进局部配点法采用基于SQP算法的SNOPT7求解器进行求解，运行环境为搭载Intel Core i5-4200 M，4 GB内存的个人计算机，编译环境为MATLAB R2015b。

4.1 定点再入

定点再入要求载人探月飞行器在指定区域开伞，同时确保气动加热和过载处于飞行器和航天员所能承受的安全范围，对轨迹优化算法的精度要求较高。假设目标开伞点的经纬度坐标为θf=100°，φf=-4°，则定义目标函数如式(28)所示：

J=(θ-θf)2+(φ-φf)2

(28)

其中，初末条件、过程约束和控制约束见表1。采用改进局部配点法可在5 s内获得满足全部约束条件的定点再入轨迹。图2～图7分别给出定点再入轨迹的三维再入轨迹曲线、速度曲线、倾侧角曲线以及过程约束曲线。

图2 定点再入三维轨迹Fig.2 Three-dimensional path of pin-point reentry

图3 定点再入时间-速度曲线Fig.3 Time-speed profile of pin-point reentry

图4 定点再入时间-倾侧角曲线Fig.4 Time-bank profile of pin-point Reentry

图5 定点再入时间-热流曲线Fig.5 Time-heat flux profile of pin-point reentry

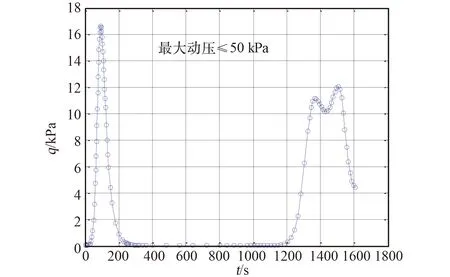
图6 定点再入时间-动压曲线Fig.6 Time- pressure profile of pin-point reentry

图7 定点再入时间-过载曲线Fig.7 Time-load profile of pin-point reentry

采用改进的局部配点法进行轨迹优化耗时约2.126 s，而且从优化结果可知再入轨迹具有典型的跳跃再入特征，最优轨迹的末端状态、过程约束等参数如表2所示。其中，末端高度10.6 km，末段经纬度为100°、 -4°，末端速度308 m/s，末端航向角为-52.6°，末端航迹角为-2.4°，满足定点再入约束；且最大热流密度为239 W/cm2，动压为16.8 kPa，过载为4.5g0/ 3.3g0。同时，最优轨迹的倾侧角曲线光滑，便于制导系统跟踪，表明算法具有良好的求解精度。此外由定点再入轨迹曲线可知，算法在轨迹变化平缓区域采用稀疏网格，在轨迹变化剧烈区域采用稠密网格，证明多分辨率技术可以有效控制离散节点的数量和分布，减小计算量。

表 2 最优轨迹末端状态和过程约束

4.2 落点区域

飞行器的再入落点区域对于评估飞行器机动能力和着陆场地的规划等具有重要意义。本文采用改进局部配点法求解最大落点区域问题，即在不同的纵向航程约束下以最大横向航程为目标函数，过程约束同表1保持一致，得到再入落点区域的边界，其中纵向航程和横向航程均为球面上的一段大圆弧。由于不考虑地球自转，正纬度方向上的再入落点区与负纬度方向上的再入落点区呈对称分布，图8给出负纬度方向上的再入落点区内的若干条边界轨迹。

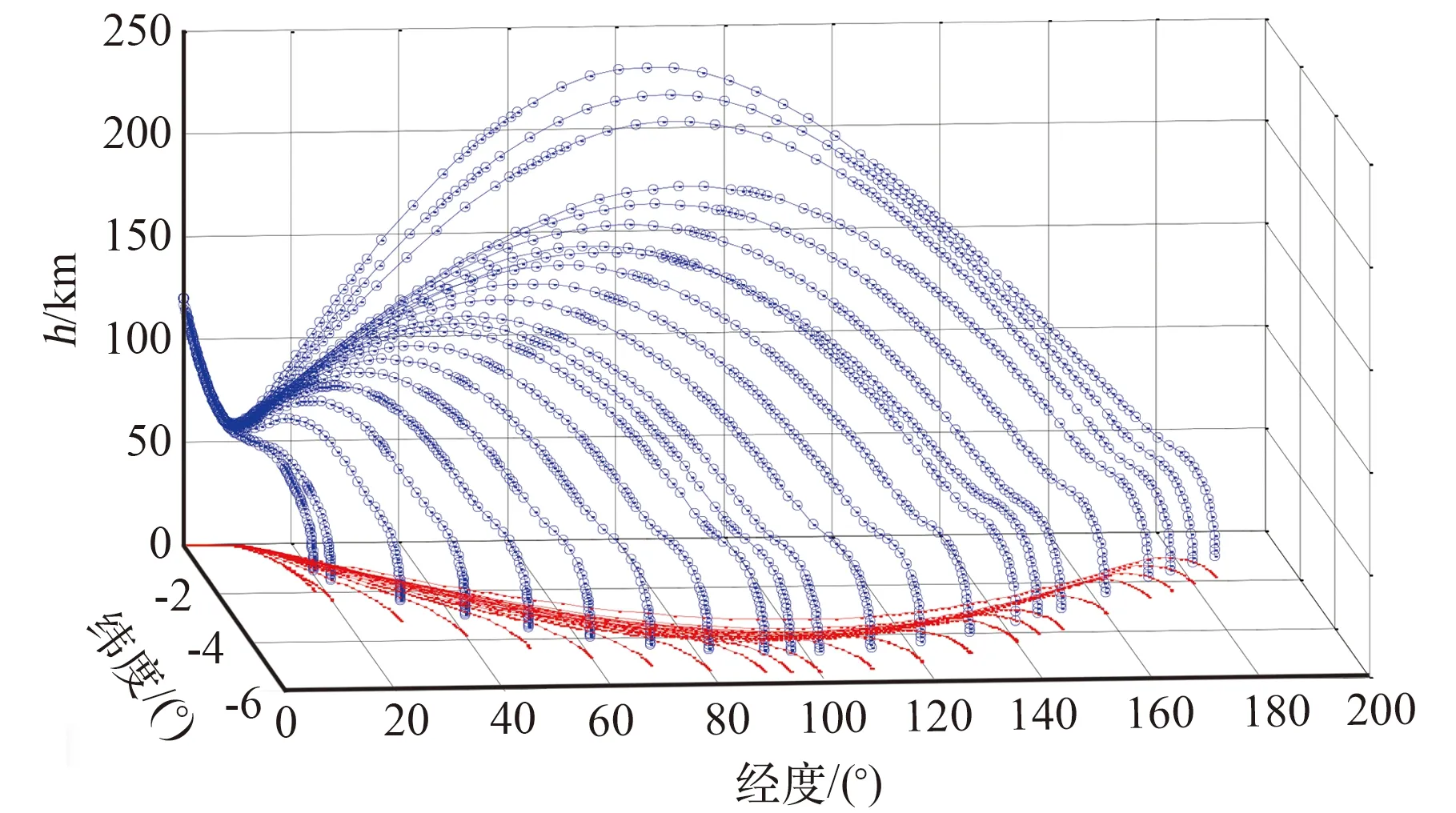
图8 落点区域右半侧边界轨迹Fig.8 Boundary paths of parachute deployment footprint

为了便于展示，图9给出了再入轨迹在经纬度平面的投影，将对应于不同纵向航程的落点区域边界轨迹的末端位置相连即可得到落点区域边界。图中红色圆圈表示返回舱的初始再入点对应的经纬度位置，即(θ0,φ0)=(0°, 0°)。可见再入飞行器的落点区域接近于椭圆形，纵向范围约为θ=18° ～ 185°(对应2001.5 ～ 20 571.1 km)，横向范围φ=-5.488° ～ 5.488°(对应-610.2 ～ 610.2 km)，飞行器能在满足约束的情况下到达落点区内的任意位置。若考虑地球自转，那么落点区域的形状会发生改变，但总体趋势一致，呈现出横向航程(或纬度绝对值)随纵向航程(或纬度)增大而先增大、后减小的特征。

图9 落点区域边界Fig.9 Boundaries of parachute deployment footprint

4.3 再入参数敏感度

实际任务中由于受到各项干扰和误差，载人探月飞行器的再入界面(或再入状态)将不可避免地偏离标准值，而飞行器的控制能力有限，因此确定当前控制能力所能承受的最大初始偏差对任务设计具有重要意义。本文参考表1飞行器的再入控制能力，仿真条件参考定点再入问题，开伞点的空间位置保持为θf=100°、φf=-4°，采用改进局部配点法研究再入轨迹对初始参数的敏感性，探讨各初始参数的允许变化范围。经过单项拉偏仿真，表3给出了再入界面的全部参数的单项最大拉偏值以及对应的最大过载和开伞点位置误差。其中初始参数的基准值为表1中各个参数的初始值，某项参数的正偏差或者负偏差是指当其他参数取基准值时，该参数允许的正向或负向最大拉偏值。拉偏值的选择是通过多次轨迹优化得到的，如以0.1 km为步长不断增大/减小高度，直到初次再入或二次再入的最大过载超过6倍和4倍g0，从而确定高度的拉偏上下极限。同理可得其余各状态量的拉偏范围。

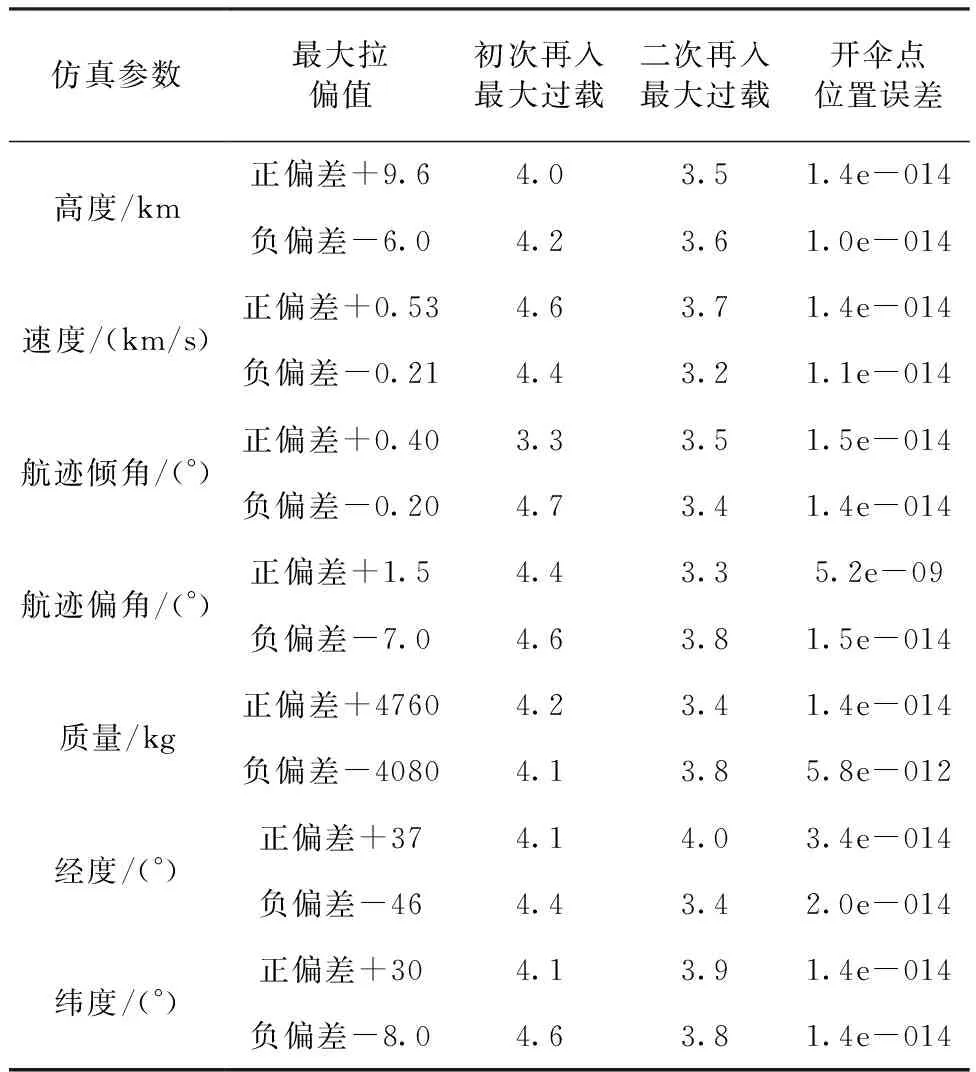
表3 再入界面变化范围

表3表明即使存在较大高度偏差或经纬度偏差，改进局部配点法仍能优化出满足定点再入约束的再入轨迹，这表明算法对于初始参数偏差具有一定鲁棒性，但过载峰值可能超出安全范围，而算法质量偏差对再入任务影响不大。此外，当飞行器控制能力给定时，定点再入轨迹对于初始速度和航迹倾角最为敏感，速度变化范围为0.21～0.53 km/s，而航迹倾角的最大变化范围为-0.2°～+0.4°，过大的速度和航迹倾角偏差将无法保证再入的过程约束和落点精度，从而威胁航天员的生命，因此为保障任务安全，必须对初始再入速度的大小和方向进行有效控制。

4.4 在线轨迹重规划

再入过程中可能发生机构故障或存在较大制导误差，本文充分利用跳跃再入的特点，基于改进局部配点法设计了在线轨迹重规划方案：当初次再入的制导误差大于给定阈值，进行二次再入界面预测，并在线重规划二次再入轨迹。在线轨迹重规划方案图如图10所示，制导控制流程如图11所示。

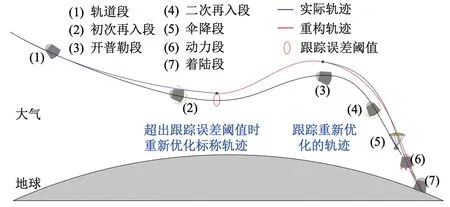
图10 在线轨迹重规划示意图Fig.10 Schematic diagram of trajectory re-planning

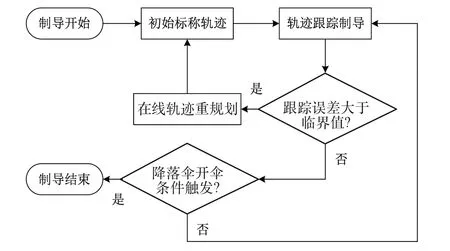
图11 在线轨迹重规划流程图Fig.11 Flowchart of trajectory re-planning

从任务背景方面来看，跳跃再入轨迹的特殊性在于飞行器由于气动力作用会跳出大气层，进行一段惯性飞行。假设大气层高度为120 km，以图12所示的定点再入轨迹为例，飞行器在大约t=450 s时跳出大气层，在大约t=1120 s时二次再入大气层，时间相差长达670 s。假设在跳出大气层时(A点)开始对二次再入轨迹进行优化，只要在飞行器进入大气层之前(B点)得到新的最优轨迹，即可用于制导算法进行跟踪，并不要求实时计算出最优轨迹。而飞行器从A点到B点的轨迹是大气层外惯性轨迹，因此可以准确预测。

图12 定点再入时间-高度曲线Fig.12 Time-altitude profile of pin-point reentry

从在线优化效率方面来看，当前离线轨迹优化耗时约5 s，在线优化时还可以利用离线优化的结果作为初值，加快收敛。目前轨迹优化算法是基于MATLAB语言，将其改为能够在嵌入式系统运行的C语言从原理上是完全可行的，并且SNOPT求解器也有C语言版本可供使用。同时，参考猎户座搭载的处理器性能(型号为PowerPC 750FX，运行速度为900 MHz，2003年发布的iBook G3个人笔记本搭载的处理器)可知，载人飞行器的计算能力已有很大提高。综上判断改进局部配点法在计算效率方面能够满足在线需求。

轨迹重规划仿真时假设二次再入时的状态变量为：r=6497.96 km，θ=69.8128°，φ=-3.1671°，V=7608.2 m/s，ψ=-1.8423°，γ=-11.3147°。以该初始状态，采用轨迹优化技术重新规划一条定点着陆轨迹(θf=100°，φf=-4°)，图13～图16给出二次再入轨迹的三维再入轨迹以及过程约束曲线，重规划轨迹的末端状态和过程约束如表4所示。

图13 轨迹重规划的三维轨迹Fig.13 Three-dimensional path of trajectory re-planning

图14 轨迹重规划的时间-热流曲线Fig.14 Time-heat flux profile of trajectory re-planning

图15 轨迹重规划的时间-动压曲线Fig.15 Time -pressure profile of trajectory re-planning

图16 轨迹重规划的时间-过载曲线Fig.16 Time-load profile of trajectory re-planning

表 4 重规划轨迹的末端状态和过程约束

4.5 算法对比

考虑定点再入问题，采用成熟的自适应伪谱法工具包GPOPS-2[22]进行轨迹优化，该方法同样采用基于SQP算法的SNOPT7求解器进行NLP问题求解，其中网格细化采用基于离散误差分析方法，计算NLP一阶偏导数采用有限差分算法。仿真中各个状态变量的初始值和取值范围参考表1，目标再入点的经纬度和4.1节保持一致，分别为θf=100°，φf=-4°，末端高度为10 km，末端速度为0.1671 km/s，采用自适应伪谱法的定点再入仿真结果如图17～图21所示。

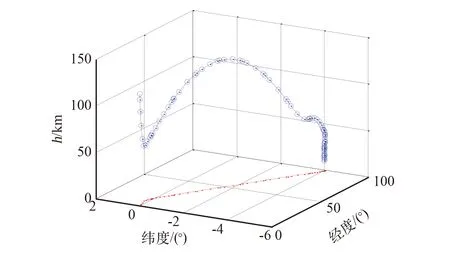
图17 定点再入三维轨迹(GPOPS-2)Fig.17 Three-dimensional path of pin-point reentry (GPOPS-2)

图18 定点再入时间-倾侧角曲线(GPOPS-2)Fig.18 Time-bank profile of pin-point reentry (GPOPS-2)

图19 定点再入时间-热流曲线(GPOPS-2)Fig.19 Time-heat flux profile of pin-point reentry (GPOPS-2)

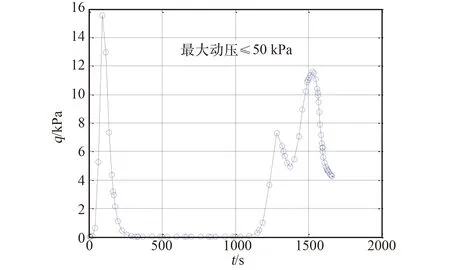
图20 定点再入时间-动压曲线(GPOPS-2)Fig.20 Time-pressure profile of pin-point reentry (GPOPS-2)

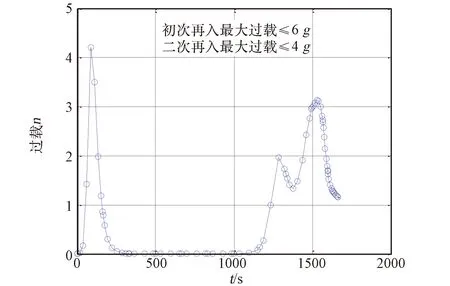
图21 定点再入时间-过载曲线(GPOPS-2)Fig.21 Time-pressure profile of pin-point reentry (GPOPS-2)

采用GPOPS-2进行轨迹规划共耗时11.78 s，但峰值热流达到300 W/cm2，超过了给定的最大热流值260 W/cm2，且倾侧角剖面变化较为剧烈。对比4.1节中改进局部配点法的定点再入性能可知，在优化精度相当的情况下，改进局部配点法的计算效率比采用全局配点的自适应伪谱法计算效率提高5倍，同时还能输出更为平滑的控制量，具有更强的过程约束和控制约束处理能力。