李 旭

(南京财经大学应用数学学院，江苏南京210023)

近些年来,随机微分方程理论被广泛应用于经济、生物、物理等领域,比如，经济领域的期权定价问题,生物领域的疾病传播问题，物理领域的逃逸与跃迁问题等。文献[1-2]对随机微分方程在许多科学领域中的重要作用进行了介绍。随机微分方程的稳定性也吸引了越来越多学者的关注，文献[3-4]对随机微分方程零解的存在性和唯一性以及渐近性质进行了详细说明，在文献[3]中，Skorohod研究了随机微分方程理论的渐近性，文献[4]对随机微分方程的稳定性理论研究的基本方法进行了论证。由于生活中的很多自然现象和社会现象都具有不确定性和受滞后影响,而随机延迟微分方程能很好地描述这些现象，即系统的演化既依赖于当前的状态，又依赖于过去的状态。文献[5-6]研究了随机延迟微分方程的几乎必然指数稳定性以及相关定理。某些突发情况的发生会导致事物的变化规律发生本质变化，因此我们引入Markov调制的随机微分方程来反映这类变化。文献[6-7]对Markov 调制的随机微分方程的分析方法和基础知识进行了具体、详细的说明。文献[8]对Markov 调制的随机微分方程的p 阶矩指数稳定性和几乎必然指数稳定性进行了深入研究。由于许多动力系统不仅依赖于当前和过去一段时间的状态，而且还依赖于过去一段时间状态的变化率，故学者们建立了Markov 调制的中立型时滞随机微分方程模型，并对此进行了广泛深入的研究，文献[9-11]给出了Markov 调制的中立型随机时滞微分方程模型的零解p(p≥2 )指数稳定性的判据，举例说明了结果的有效性，并用欧拉算法论证了该模型零解的收敛性。目前，大部分讨论了中立型时滞随机微分方程模型在线性增长条件和一致条件下模型零解的p(p≥2 )阶矩渐进有界性和p(p≥2 )阶矩指数稳定性，对于p的取值范围有所局限。但对于p(0 ＜p≤2 )的p阶矩渐近有界性和p阶矩指数有界性的研究尚缺乏。因此，将研究Markov 调制的中立型时滞随机微分方程在延迟项为连续函数条件下p(0 ＜p≤2 )阶矩指数稳定性成立的几个新的判别准则。

1 模型与假设

其中 Δ ＞0,γij≥0 是从状态 i 到状态 j 的转移概率，如果 i ≠ j，则 γii=

Markov 调制的中立型变时滞随机微分方程模型如下：

满足初值条件

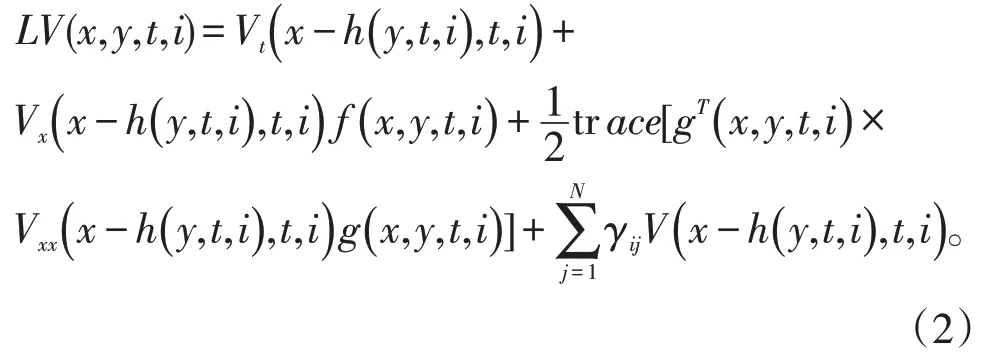
为了得到我们的结果，需要以下假设：

ℏ1:存在常数κi∈(0,1), 使得对于任意的 x,y ∈Rd,成立，且h( )0,t,i =0。由此可得：

ℏ3：对于 x,y ∈Rn,t ∈R+,i ∈S, 存在函数V(x ,y,i)∈C2,1(Rd×R+×S；R+)，q,p 满足：1 ≤p ＜q，非负常数c1,c2,aj(0 ≤j ≤4 )，且下列式子成立：

ℏ4：对于 x,y ∈Rn,t ∈ R+,i ∈S, 存在函数 V(x,y,i) ∈C2,1(Rd×R+×S；R+)，q,p 满足：0 ＜p ＜q ≤1，非负常数c1,c2,aj(0 ≤j ≤4 )，且下列式子成立：

2 渐近有界性和指数稳定性

定义1如果对于任意 ξ ∈Rd，存在 η ＞0 使得：那么称方程（2）零解 p阶矩指数稳定。

定义2若存在常数 μ ≥0（与 ξ 无关），使得：

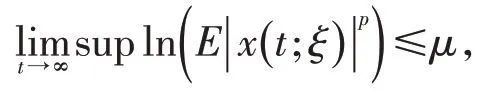
那么称方程（2）零解p 阶矩渐近有界的。

定理 1若假设 ℏ1,ℏ2,ℏ3成立，且满足如下不等式：

对 0 ＜ γ ＜ γ1∧ γ2＜成立，其中 γ1是方程

唯一的正根，γ2是方程

唯一的正根。

证明令R0＞0,且R0是一个满足式子：

R0≥‖ξ‖的足够大的一个常数，停时：ρR=inf应用公式可得：

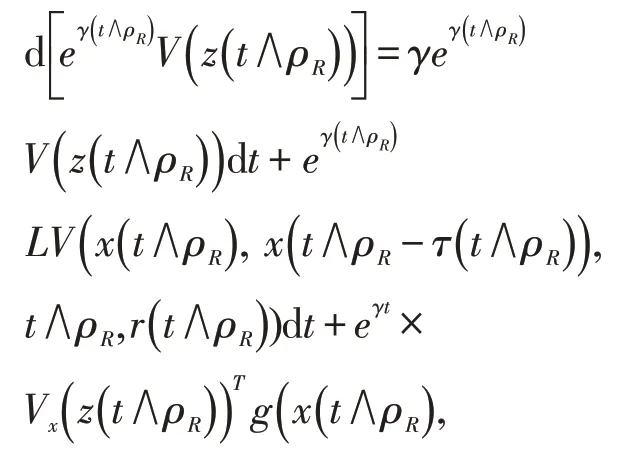
由假设ℏ3可得：

取ε=κp-1，则有：

其中

成立，则我们可得：

设

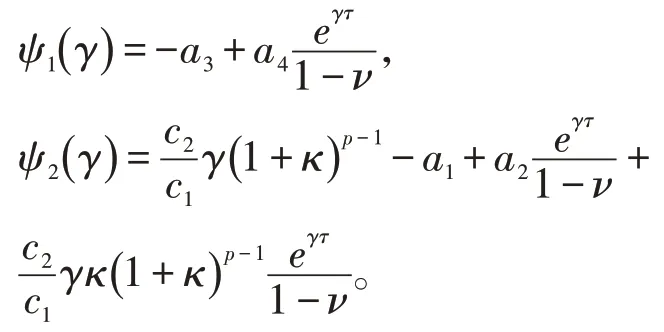
因此，对任意 γ ＜γ1∧γ2，我们有：

其中R 为常数，又因为ε ＞0，有

因此，对 0 ＜s ＜t：

由 γ ＜ γ1∧ γ2＜可知，存在正数 εi＞0，使得：

因此，可得：

即

因此由(5)即可推出（4），完成了 p 阶矩指数稳定性的证明。

引理 1若假设 ℏ1成立，且 1 ≤p ＜2，x,y ∈Rd，t ∈ Rd，i ∈ S ，则

推论1假设 ℏ1、ℏ2、ℏ3成立，且满足如下不等式：

方程(1)是零解p 阶矩渐近有界的，

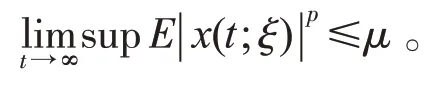
的唯一正根。此外，当a0=0 时，方程的零解是 p阶矩指数稳定的(η=ω)。

证明Markov 调制的中立型变时滞随机微分方程模型的零解p(1 ＜p ≤2 )阶矩稳定性同文献[11]中p(p ≥2 )中Markov 调制的中立型变时滞随机微分方程证明过程相同。

定理 2假设 ℏ1、ℏ2、ℏ4成立，且满足如下不等式：

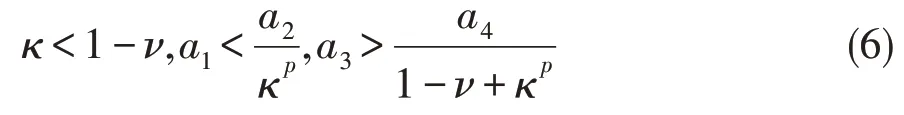
方程(1)是零解 p 阶矩渐近有界的，

证明令R0＞0,且R0是一个满足式子：R0≥‖ ξ‖ 的足够大的一个常数，停时：则应用 Ito∧公式和假设 ℏ4可得：

利用（6），可得：

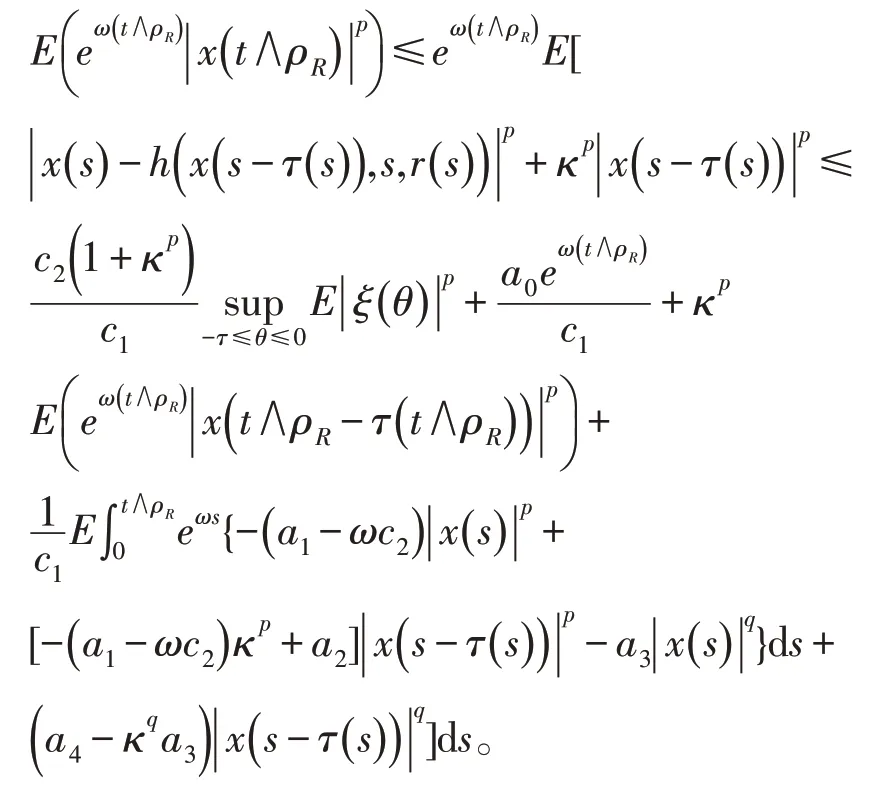
根据假设ℏ2可得如下积分不等式：

因此，记：

我们可得：

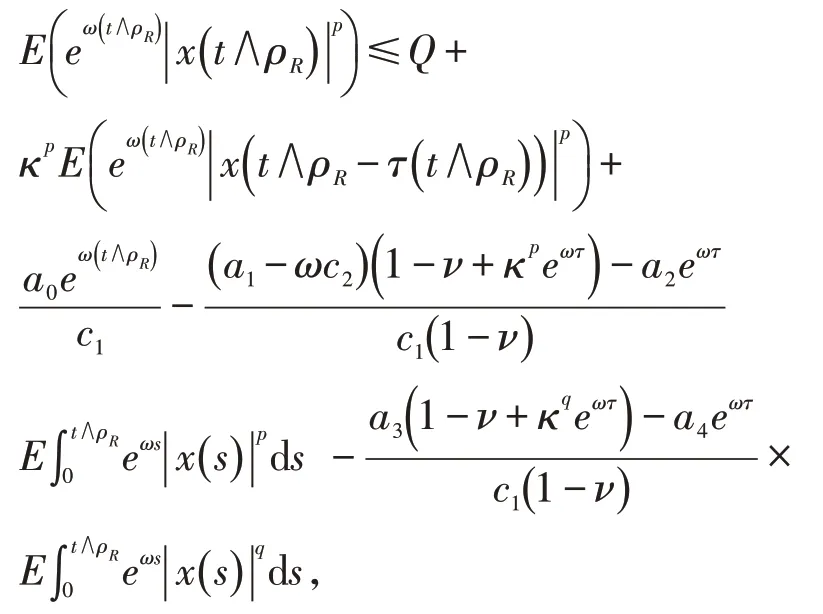
令

由(7)可知，F( ω1) 是连续且单调递减的，且满足：

因此根据(8)可知，有唯一的正根 ω1，对于 ω ＜ω1∧可得：

令R →∞，由Fatou引理可得：

对任意T＞ 0，有

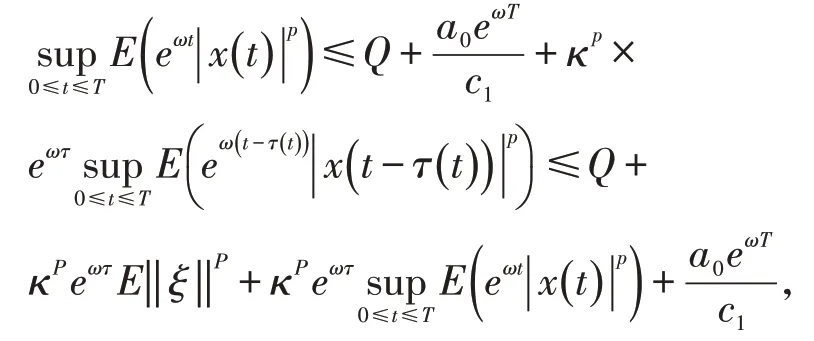
因此

由(9)可知方程（1）零解的 p 阶矩指数渐近有界性成立。当a0=0 时，由(10)可直接推断出零解的 p阶矩指数稳定性成立。

3 应用

例1 构造延迟项为τ( t )=0.9t 的 Markov 调制的中立型变时滞随机微分方程：

取

经计算得，

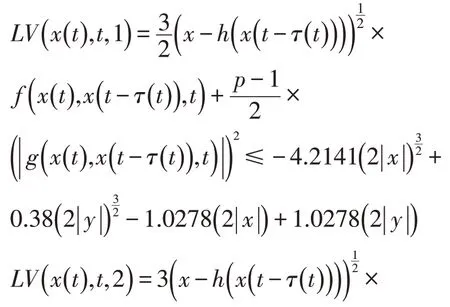
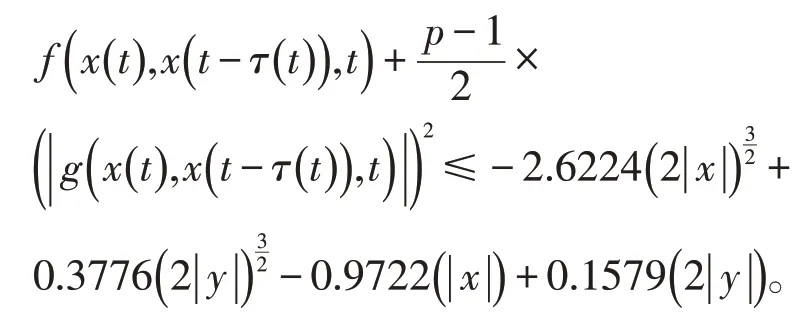
已知

例2 构造延迟项为τ(t)=0.5t 的 Markov 调制的中立型变时滞随机微分方程：

取

经计算得，

因此根据定理2可知方程解的零解p(0＜p≤1)阶矩稳定性成立。

4 结论

将Markov 调制的中立型时滞随机微分方程 p阶矩稳定性和矩有界性结果从 p(p ＞2 )推广到p(0 ＜ p ≤ 2 ), 扩大了 p 的取值范围； 把时滞项为常数变为连续函数,提高了模型的实用性。接下来可以研究带Possion 跳和Markov 调制的中立型时滞随机微分方程的p 阶矩稳定性结果，将其模型的稳定性从p(p ＞2 )推广到 p(0 ＜ p ≤ 2 ), 扩大 p 的取值范围，并把时滞项为常数变为连续函数, 研究此模型下零解的存在唯一性和稳定性情形。