两向不等压巷道围岩塑性区近似解及数值模拟

2019-12-16董海龙高全臣陈汝博

煤炭学报 2019年11期

董海龙，高全臣，张赵，陈汝博，刘娜

(中国矿业大学(北京)力学与建筑工程学院，北京 100083)

巷道开挖引起围岩应力的二次分布，二次应力状态往往会超出岩体屈服强度而产生塑性区[1]，围岩塑性区的确定是巷道稳定性评估及支护参数定量的重要依据之一，选择合理且符合工程实际的算法至关重要。

长期以来，两向不等压巷道围岩塑性区的求解问题一直没有得到很好的解答，常用的方法主要有:① BEELLO-MALDONADO[2]、孙广忠[3]、蔡晓鸿[4]及孙金山[5]等以轴对称应力场塑性区应力公式为基础，结合既有弹性解构造应力分量表达式并得出塑性边界解(为表述方便，本文称之为应力构造法)。② KASTNER[6]将依照弹性理论求解的弹性围岩应力直接代入塑性条件得到塑性区边界的近似隐式方程(本文称之为近似隐式法)。几十年里，这一方法一直被广泛运用，尤其是近年来赵志强[7]提出“蝶形塑性区”概念以来，近似隐式法得到了很好的继承、发展与应用，并由此形成了“蝶形塑性区”理论[7-12]，为巷道稳定性评估及支护方案的设计等提供了有力的理论支撑。③ 鲁宾涅依特[13]、魏悦广[14]及侯公羽等[15]则采用小参数法对两向不等压圆洞塑性区问题进行研究。④ 一些学者[16-17]运用复变函数理论对这一课题展开研究。各类方法各有其优缺点。其中，应力构造法求解相对简单，便于工程实践应用，但它一般将两向不等压圆巷围岩塑性区的力学模型视为轴对称平面应变问题，这显然是不严谨的。近似隐式法虽能够较好反映塑性区形状随侧压系数的变化规律，一定情况下会出现与大量数值模拟实际相仿的“蝶形”塑性区;然而，将侧压系数λ=1代入近似隐式方程得到两向等压圆巷围岩的塑性区半径，并与基于成熟轴对称平面应变理论得到的塑性区解析半径对比，可以发现前者存在较大的理论误差。复变函数法以“塑性区为囊括巷道边界的连通域”为前提不完全合理。小参数法不但计算复杂，而且侧压系数的合理取值范围较小，严重制约其在工程实际中的应用。解析算法作为确定巷道围岩塑性区范围的一种有效手段，非常有必要对其误差进行评估，以确保所得塑性区范围的准确性与可靠性。但遗憾的是，鲜有学者对这一问题进行相应的研究或探讨[16]。

基于这一背景，笔者以数值模拟结果为参考，连同复变函数法的解析结果，对应力构造法和近似隐式法的准确性展开初步的探讨，旨在寻求更为准确的求解两向不等压巷道围岩塑性区范围的算法。

1 理论分析模型与基础

1.1 力学模型

为避免问题过于复杂，假定:① 巷道围岩连续、均质且各向同性;② 巷道为深埋圆形平巷，长度无限大;③ 巷道处于两向不等压地应力场中，支护荷载为均匀荷载，不计重力梯度的影响;④ 岩体为理想弹塑性材料，且塑性破坏满足Mohr-Culomb强度准则。

基于上述假定，所研究问题可简化为如图1所示的平面应变力学模型。为便于表述，对模型基本参数作如下规定:a为巷道半径;r为围岩质点到巷道中心的距离;θ为极角;Rp为对应极角θ的塑性区半径;Pi为支护荷载;P0为竖向原岩应力;λ为侧压系数;σr，σθ分别为围岩径向、切向应力;R0，R90分别为水平、竖向轴上的塑性区半径。此外，弹、塑性区相关参数用下标i(i=e,p)区分表示。

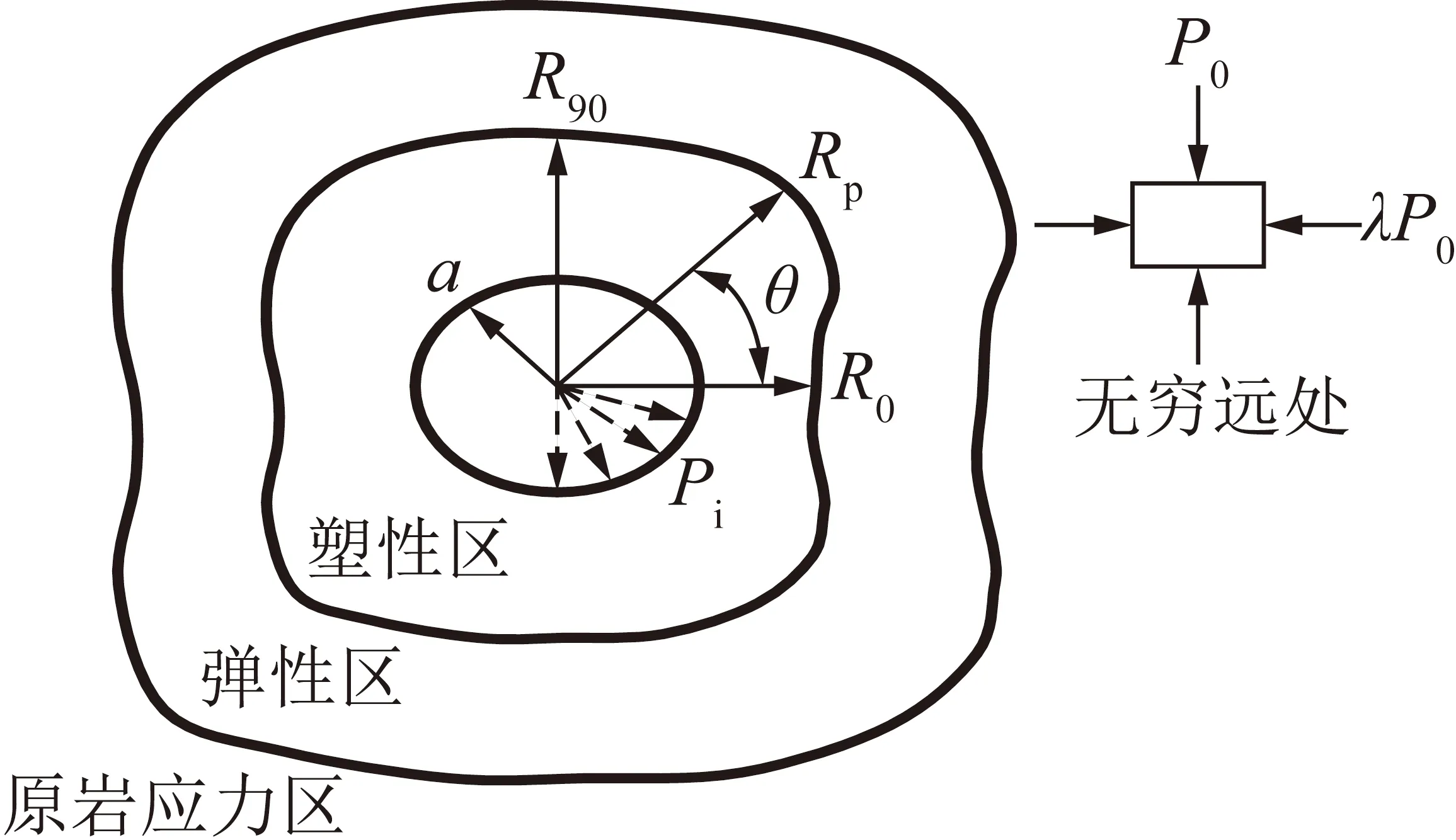
图1 巷道力学模型(λ>1)

1.2 λ=1时巷道围岩弹塑性解析

λ=1时，圆巷围岩弹塑性解析可简化为轴对称平面应变问题，目前对该问题的研究已较成熟，为行文简洁起见，此处不再赘述，根据文献[18]，结果如下:

围岩弹性区应力为

(1)

其中，R为λ=1时圆巷围岩塑性区半径。弹塑性交界处的径向应力为

σr|r=R=(2P0-B)/(A+1)

(2)

式中，A=(1+sinφ)/(1-sinφ);B=2Ccosφ/(1-sinφ);φ为岩体内摩擦角;C为黏聚力。

围岩塑性区应力为

(3)

式中，N=B/(1-A)。

塑性区半径为

(4)

2 λ≠1时巷道围岩塑性区近似解

长期以来，两向不等压圆形巷道围岩塑性区的求解问题一直采用近似算法，其中应力构造法和近似隐式法常有运用。特别是以近似隐式法为基础形成的“蝶形塑性区”理论，被广泛运用于巷道围岩的稳定性分析、支护设计和冒顶灾害防治等工程实践。下面就两种方法的解析过程及其结果的准确性展开分析与探讨。

2.1 应力构造法及其评估

2.1.1应力构造法的解析

在两向不等压应力场岩体内开挖巷道，促使岩体应力二次分布，若二次应力未达到岩体起塑条件，则巷道围岩仅发生弹性变形。两向不等压圆巷围岩的弹性应力[1]为

(5)

式中，x=a2/r2。

若二次应力超出岩体的屈服强度而出现弹、塑性状态并存的分布特点，围岩的弹塑性解析就要复杂的多。就围岩产生的塑性区而言，一些学者[2-4]认为，由于初始地应力为远方荷载，围岩塑性区主要取决于岩体屈服的极限平衡条件，初始地应力影响甚微。因此，可将塑性区的力学模型视为轴对称平面应变问题进行求解。如此，两向不等压圆巷围岩塑性区应力仍可用式(3)近似。同时，假定围岩塑性区以外的弹性区应力仍服从式(5)，只需将a替换为塑性区半径rp，支护荷载Pi替换为σr|r=R即可。由此可得围岩弹性区的切向应力为

(6)

式中，rp为应力构造法确定的两向不等压圆巷围岩塑性区半径。

再根据围岩应力接触条件σθe|r=rp=σθp|r=rp，联立式(3)，(6)即可得塑性区半径为

rp=a[(1+λ)P0+2(1-λ)P0cos 2θ-

(7)

2.1.2应力构造法的评估

上述应力构造法解析中，两向不等压圆巷围岩塑性区的应力，是依据轴对称平面应变理论求解的。这样求解的前提之一是塑性区为轴对称的圆形，但显然这一前提不成立;并且假定塑性区以外弹性区应力仍为式(5)的形式也是没有理论依据的。可见应力构造法并不是准确的解析算法。此外，由于λ>1的力学模型经旋转90°后等效于1/λ<1的情况，故不失一般性，下面以λ≤1的情况为例对其准确性展开分析。

为使分析结果直观化，本文实例均以文献[17]为准，基本参数如下:a=2 m，P0=15 MPa，Pi=0 MPa，C=1 MPa，φ=30°，λ无特殊说明时为2/3。

取λ为0.3,0.4和0.5，并将实例参数代入式(7)得到应力构造法确定的塑性区，如图2(a)所示。

将图2(a)与下文图3等条件下的数值模拟结果对比，可以发现:λ=0.3,0.4,0.5时，二者塑性区在形状上相差非常大;但二者水平轴上的塑性区半径相差并不大，这一点也可由下文表1～3的数据对比发现。这表明:λ=0.3,0.4,0.5时，应力构造法仅能确保围岩在水平轴上塑性区半径的精度，其余位置并不准确，甚至偏差非常大。

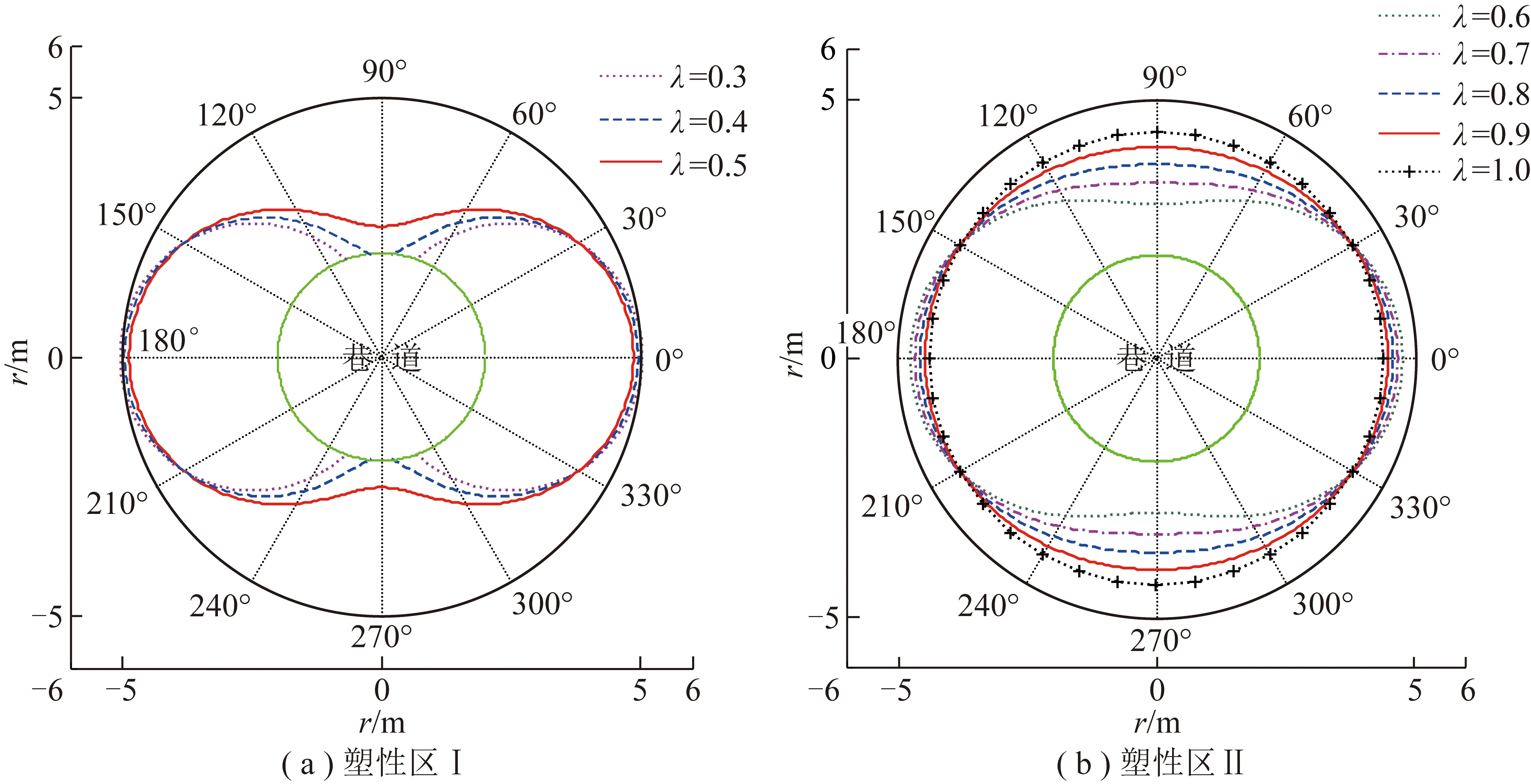
图2 应力构造法塑性区Ⅰ,Ⅱ

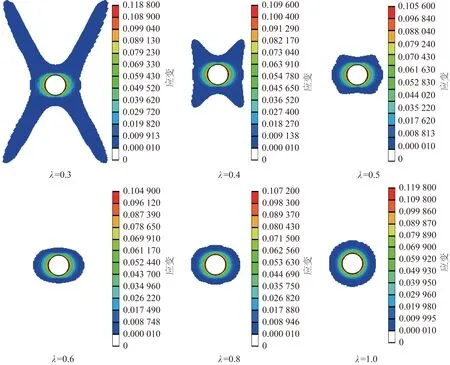
图3 数值模拟结果

表1 不同黏聚力的水平轴上塑性区半径

Table 1 Plastic radius on horizontal axis for different cohesions

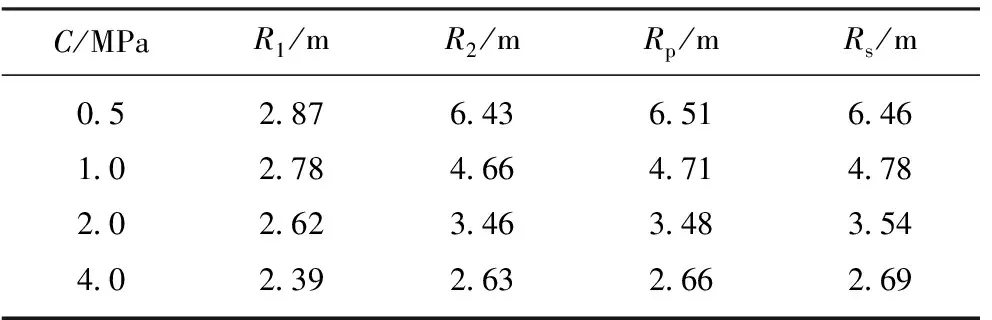
C/MPaR1/mR2/mRp/mRs/m0.52.876.436.516.461.02.784.664.714.782.02.623.463.483.544.02.392.632.662.69

表2 不同φ的水平轴上塑性区半径

Table 2 Plastic radius on horizontal axis for differentφ

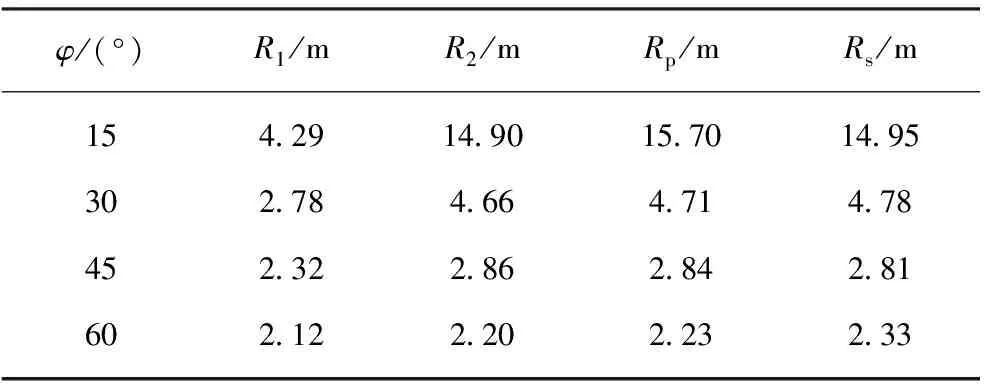
φ/(°)R1/mR2/mRp/mRs/m154.2914.9015.7014.95302.784.664.714.78452.322.862.842.81602.122.202.232.33

表3 不同λ的水平/竖向轴上塑性区半径

Table 3 Plastic radius on horizontal axis for different lateral coefficients

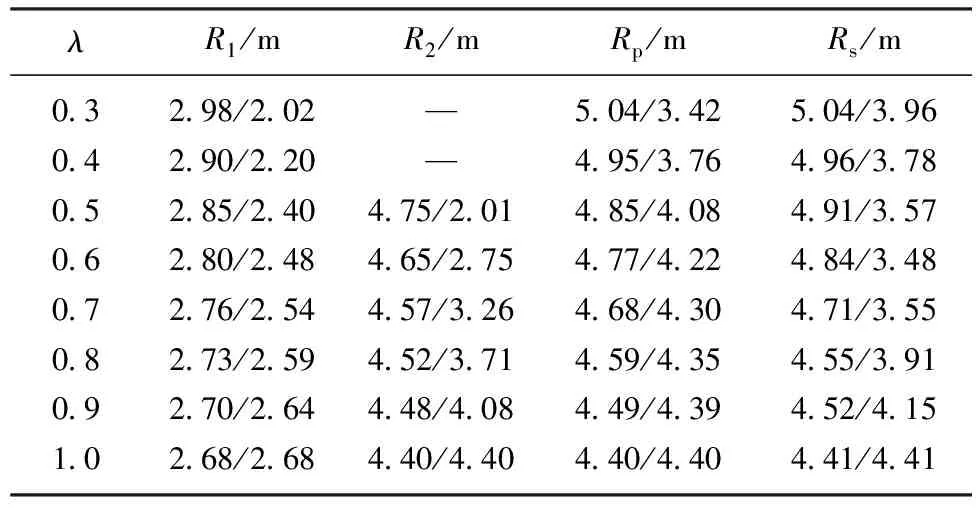
λR1/mR2/mRp/mRs/m0.32.98/2.02—5.04/3.425.04/3.960.42.90/2.20—4.95/3.764.96/3.780.52.85/2.404.75/2.014.85/4.084.91/3.570.62.80/2.484.65/2.754.77/4.224.84/3.480.72.76/2.544.57/3.264.68/4.304.71/3.550.82.73/2.594.52/3.714.59/4.354.55/3.910.92.70/2.644.48/4.084.49/4.394.52/4.151.02.68/2.684.40/4.404.40/4.404.41/4.41

再取λ为0.6,0.7,0.8,0.9和1.0，类似可得应力构造法确定的塑性区范围，如图2(b)所示。

由图2(b)可知，围岩塑性区在λ=1时为圆形;λ=0.6～1.0时近乎于椭圆，这与图6等条件数值模拟结果基本一致。为进一步分析应力构造法所得塑性区是否准确，将(椭)圆短轴取出，并与数值模拟结果对比，见表4。分析表4可知:随着λ不断靠近1，应力构造法相对于数值模拟法的误差逐渐减小，在0.7～1.0范围内，应力构造法求解的塑性区较准确。并且，相对于吕爱萍等[17]基于复变函数法给出的有关结果，应力构造法与数值模拟结果吻合得更好。

表4 “椭圆形”塑性区短轴对比

Table 4 Short axis comparison of elliptical plastic zone

参数λ0.60.70.80.91.0应力构造法/m2.993.403.764.094.40数值模拟/m3.483.553.914.154.41相对误差/%16.44.44.01.60.2复变函数法/m2.753.293.714.084.40

此外，λ>1的情况与λ≤1时基本类似，即λ>1时应力构造法仅能确保围岩在竖向轴上塑性区半径的精度。因此，λ≤1(或λ>1)时，圆巷围岩水平(或竖向)轴上的塑性区半径可由应力构造法准确确定，即将θ=0°或90°分别代入式(7)得

(8)

综上，应力构造法虽存在一定的理论缺陷，但在λ=1的某个邻域内较准确，而该邻域外准确度较低，甚至偏差很大。同时，应力构造法能够确保λ≤1(或λ>1)时围岩在水平(或竖向)轴上塑性区半径的精度，这主要是水平(或竖向)轴上剪应力为0，计算条件与轴对称应力场完全一致的缘故。

2.2 近似隐式法及其评估

大量数值模拟结果[7-12]表明，一般在λ=1的某个邻域内(本文实例大致在0.6～1.5范围内)，圆形巷道围岩塑性区近似为(椭)圆，此时，应力构造法求解的塑性区较准确;但在该邻域以外，巷道角部塑性区快速发展，形成“蝶形”形状，应力构造法求解的塑性区形状就存在很大的偏差。可见，应力构造法虽能确保围岩在水平(或竖向)轴上塑性区半径的精度，却无法反映围岩塑性区形状随λ的变化情况。为解决这一问题，下面引入近似隐式法。

2.2.1近似隐式法的解析

近似隐式法是目前相关理论研究的主流方法之一，其求解的圆巷围岩塑性区在一定条件下会出现圆形、椭圆形和蝶形等形态，能够较好地反映圆巷围岩塑性区一般形态的变化规律[7-12]。其解析过程如下:

主应力与各应力分量间的关系[12]为

(9)

式中，σ1,σ3分别为最大、最小主应力。

将式(9)代入Mohr-Coulomb准则方程σ1=Aσ3+B可得以参量A,B及应力分量表示的准则方程

(A-1)+2B

(10)

然后将围岩弹性应力表达式(5)直接代入式(10)，整理后就可得塑性区边界的隐式方程为

f(x)=k0+k1x+k2x2+k3x3+k4x4=0

(11)

由于近似隐式方程非常复杂，无法直接求出塑性区半径的解析式。但对于实际工程问题，可借助Matlab,Maple等数学软件求解式(11)的数值解析解，进而确定巷道围岩塑性区范围。值得一提的是，在数值计算过程中，式(11)通常存在4个根(重根除外)，可采取“去虚就实，前后对比”的原则进行选根。即去除不合理的虚根，对于存在多个实根的情况，可对比附近角度(如θ=θ±5°)已确定的塑性区半径大小进行合理地选根。

2.2.2近似隐式法的评估

由于λ≠1条件下，圆形巷道塑性区并不是圆形，近似隐式法仍假定弹性区应力为式(5)的形式其实是没有理论依据的;将弹性应力直接代入塑性条件来确定塑性区范围，也是有待商榷的。因此，近似隐式法也不是准确的解析算法，其误差大小需要进一步研究。

为此，不妨将λ=1代入近似隐式方程得到两向等压时圆形巷道围岩塑性半径的解析式为

(12)

式中，R1为近似隐式法确定的两向不等压圆巷围岩塑性区半径。

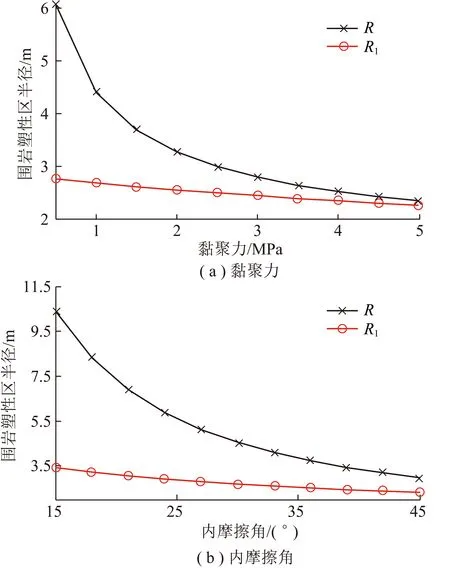
图4 近似隐式法理论误差

这与基于轴对称平面应变理论的塑性区解析半径R的解析(式(4))并不相等;并且，代入上述实例参数对比计算可以发现，二者相对误差较大，如图4所示。

从图4(a)可以明显看出，近似隐式法在λ=1处存在较大的理论误差，特别是对于深软巷道围岩塑性区，其误差更大。如令P0=30 MPa，C=0.5 MPa，φ=25°时，得到相应R在13 m以上，而R1仅约为3.02 m，整整相差3倍多。

综上，近似隐式法虽缺乏理论依据，但其能较好地反映圆巷围岩塑性区一般形态的变化规律，对于巷道围岩状态的估算有一定意义。值得注意的是依据近似隐式法求解的塑性区大小存在较大误差。

2.2.3近似隐式法的修正

近似隐式法在λ=1时固然存在较大的理论误差，但目前并没有其它很好的办法用以确定两向不等压圆形巷道围岩塑性区的形状。考虑到式(8)确定的塑性区半径在λ=1时不存在理论误差，本文仍以近似隐式法为基础确定围岩塑性区的形状，再结合上述推导的R0与R90，根据相似原理，最终相对准确地确定两向不等压圆巷围岩的塑性区半径为

(13)

式中，R1|θ=0°和R1|θ=90°分别为近似隐式法确定的围岩水平及竖向轴上的塑性区半径。

式(13)为本文给出的两向不等压圆巷围岩塑性区半径。它不但消除了近似隐式法在λ=1时的理论误差，同时继承了近似隐式法能够较好反映塑性区形状变化规律的优点。

3 算法的准确性分析

3.1 数值模拟分析

为验证算法的准确性，首先采用有限元软件Abaqus建立二维模型模拟圆巷围岩塑性区的分布。模型选用M-C准则，输入材料参数如下:弹性模量E=4 GPa、泊松比μ=0.25、密度ρ=2.5 g/cm3、黏聚力C=1 MPa、内摩擦角φ=30°。模拟主要步骤有:① 建模，模型尺寸为50 m×50 m，圆形巷道位于模型中央，半径为2 m；② 施加载荷与边界条件，模型顶部边界施加15 MPa均布竖向载荷，用以模拟上覆岩层重力引起的荷载，忽略模型自重，模型底边设置竖直方向位移为0，左右边界设置水平方向位移为0；③ 网格划分，采用四边形平面应变单元将模型划分为16 602个单元，并对巷道周边的单元进行细化，单元划分整体呈内密外疏的辐射状，辐射基数为6；④ 模拟计算，模拟计算分为初始地应力平衡和巷道开挖2个步骤:由于模型为规则的正方形，简单添加预应力场即可实现地应力的平衡，竖向地应力设置为15 MPa不变，侧压由λ控制，λ以0.1为步长由0.3递增至1.0，应力平衡后方可进行后续计算;巷道开挖采用单元生死技术实现；⑤ 结果与分析。

考虑到λ=1时的圆巷围岩弹塑性理论研究已较成熟，因此，先以λ=1为例，对数值模拟结果的误差作简要分析，以验证数值模拟结果的准确性。

在θ=0°由巷道内缘到模型边界的直线路径上，均匀地取100个节点，将各节点应力的数值与理论结果(理论结果见1.2节)绘制于同一坐标系下，如图5所示。

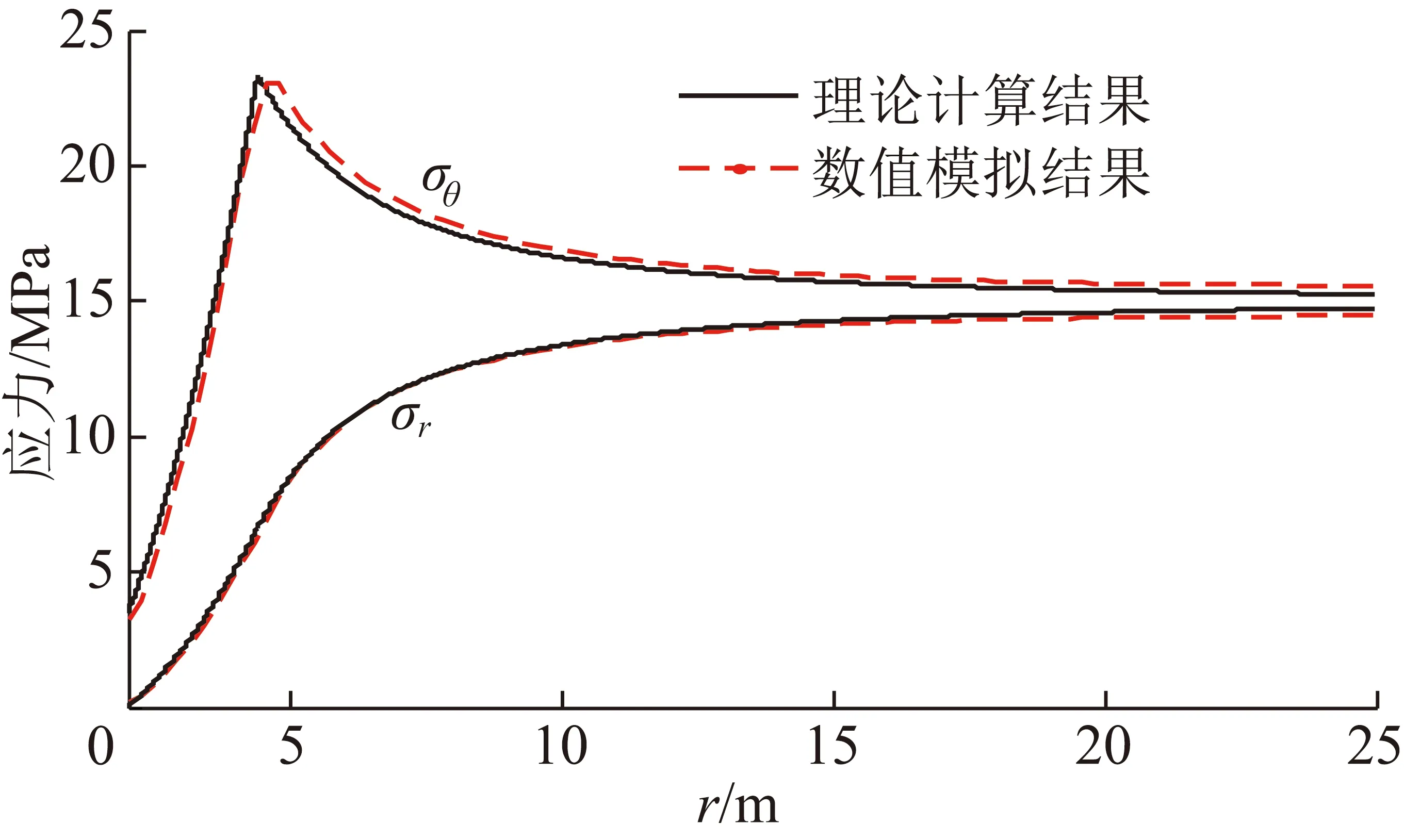
图5 数值模拟结果准确性验证

从图5可以看出，λ=1时巷道围岩应力分布的理论与数值模拟结果非常接近。可见，数值模拟结果较为准确，可以之为基础，对不同算法得到的λ≠1时巷道围岩塑性区半径的准确性进行验证。

计算机一般将10-5视为0，因此，以塑性应变等于10-5为基准确定巷道围岩塑性区边界，得到数值模拟的不同λ下围岩塑性区的分布情况，如图2所示。

图2表明:λ<1时塑性区主要向巷道两帮发育;围岩塑性区在λ=1时为圆形;0.5～1时，近乎于椭圆;小于0.5以后，巷道角部塑性区快速发展，形成“蝶形”形状，模拟结果与有关文献[7-10]基本类似。

3.2 算法准确性对比

前文提及在λ偏离1较大时，应力构造法确定塑性区形状存在很大的偏差。为此，此处以λ=0.3，0.4为例，就不同算法得到的塑性区范围进行对比，结果如图6所示。分析图6可知，λ=0.3,0.4时应力构造法在塑性区的形状上存在很大偏差;近似隐式法在塑性区的大小上误差较大;而本文算法虽与数值模拟结果仍存在一定的误差，但已基本能反应围岩塑性区的分布情况。

图6 不同算法塑性区对比

目前，以近似隐式法为基础的“蝶形塑性区”理论的研究已较成熟[7-12]，就两向不等压巷道围岩塑性区形状的确定来讲，近似隐式法有其优越性，故重点对其求解的塑性区大小进行探讨。为避免误差分析的偶然性，采用单因素法，对围岩水平(或竖向)轴塑性区半径受C，φ及λ的影响进行分析，以期获取相对准确的结论(表1～3)。R1，R2，Rp和Rs分别为由近似隐式法、文献[17]复变函数法、式(13)及有限元法确定的相应塑性区半径。

从整体上看，本文算法与数值模拟结果吻合最好，R2次之，R1最差。这说明:

近似隐式法不仅在λ=1时存在较大的理论误差，而且在λ≠1时也同样存在较大的误差。可见，近似隐式法虽可较好地反映围岩塑性区形状随λ的变化规律[6-11]，但其求解的塑性区大小并不准确。因此，本文在近似隐式法的基础上，根据相似原理，消除其在λ=1时的理论误差，使算法的准确性得到一定程度的提升，具有一定的理论和工程实用价值。

本文算法求解的水平(或竖向)轴上塑性区半径，是应力构造法在θ=0°(或90°)时的特例，即R0(或R90)，其与利用有限元法及复变函数法得到的相应结果都良好吻合。但通过图2(a)与图6的对比可知，除能保证R0(或R90)的精度外，应力构造法求解的其余位置塑性区半径并不准确，甚至偏差非常大。因此，本文算法结合近似隐式法对应力构造法的塑性区形状进行优化，具有重要意义。