刘春书

求线段长度的范围是初中数学常见的一类问题，对于此类问题通常有两种通法.一是建立关联，控制一个量的范围求线段的长度范围;二是化归轨迹，通常有两类，一动点到一定点或一动点到一动点.下面结合2019年南京市中考题填空压轴题（第16题）谈谈如何变换问题基于属性觅得思路.

题目 （2019南京）在△ABC中，AB=4，∠C=60°，∠A>∠B，则BC的长度范围为.

1 分析及解法

本题文字简洁、内涵丰富、方法多样，是一道压轴题，得分率只有0.1.此题以三角形边角关系立意，△ABC一边和其对角确定，其它元素不确定，即∠A、∠B、AC、BC是变化的.对于变化的问题，可以从形的角度进行图形直观，基于变化寻找临界位置，BC是三角形的边，点B确定，点C是一动点，本问题就可以转化为求动点C到定点B距离的范围，即探索点C的轨迹，基于临界位置确定范围;也可以从数的角度进行逻辑推理，就是建立关联，控制变量研究范围，明晰BC随哪个量变化而变化，再基于变化范围寻求线段的长度范围，即建立函数关系，采用控制变量法.

1.1 基于经验分析

轨迹视角：探索轨迹，基于临界确定范围.

分析条件——研究条件的定与变：

分析问题：BC是什么？BC与哪些量存在关系？

思路1：BC是△ABC的外接圆⊙O的弦，由于60°<∠A<120°，点C在AC′上，当BC为直径时，BC最长为8 33.当点C与C′重合时，BC最短为4.当点C与点A重合时，BC最短为4，即4

函数视角：建立关系，基于范围寻求范围.

分析条件——研究条件的定与变：

分析问题：BC是什么？BC与哪些量存在关联？

思路2：BC是△ABC的一边，BC的长度随∠A的大小变化而变化.基于这两个信息，可以用高中的正弦定理.即BC sinA=AB sinCBC=ABsinA sinCBC=4sinA sin60°BC=83sinA 3，因为60°<∠A<120°，所以3 2[SX）]

思路3：BC是△ABC的一边，BC的长度随∠A的大小变化而变化.线段与角度的关系需要建立三角函数进行解决.在初中阶段将斜三角形化归直角三角形，作三角形的高构建所求边的相关三角函数进行解决.如图1，作△ABC的高BH，在Rt△BCH中，可得sinC=BH BC，即BC=BH sinC=23[KF）]BH 3[SX）].在Rt△ABH中，由于60°<∠A<120°，由图1可知AB·sin60°

1.2 解法

解法1：如图2，因为∠A>∠B，又因为∠A+∠B=180°-∠C=120°，所以∠B<60°<∠A<120°，作以AB为边的等边△ABC′的外接圆⊙O.因为∠C′=60°，所以点C在AC′上，当BC为直径时，BC最长为83[KF）] 3，即4

解法2：如图1，作△ABC的高BH.在Rt△BCH中，BC=BH sin60°.因为∠CAB>∠ABC，

又因为∠CAB+∠ABC=180°-∠C=120°，所以∠CAB>60°>∠ABC，Rt△ABH中，因为BH=AB·sin∠BAH.又因为60°<∠BAH≤90°，所以3[KF）] 2[SX）]AB

一个三角形一边及其对角确定，此三角形的外接圆是确定的，另两个角的大小范围是确定的，两条边的长度范围也是确定的.为研究本质有必要进行一般化思考，一般化有两个方向：一是去∠A>∠B的条件，二是定边的对角的大小一般化.因此本題可以变式如下.

变式1 在△ABC中，AB=4，∠C=60°，则BC的长度范围为.

经验1轨迹视角：探索轨迹，基于临界确定范围.如图3，易得0

经验2函数视角：建立关系，基于范围寻求范围.如图4，因为BC=BH sinC=23[KF）] 3BH（0

变式2 在△ABC中，AB=4，∠C=m°，则BC的长度范围为.

经验1轨迹视角：探索轨迹，基于临界确定范围.如图5，当0

经验2函数视角：建立关系，基于范围寻求范围.BC的长度与∠C的大小有关，当m°≥90°时，则0°<∠A<90°<∠C，所以AB·sinA

3 对解题教学的几点思考

3.1 引导学生从定与变的视角分析条件

综观此题分析及解答的过程，从知识技能层面看，此题主要考查解三角形、圆、三角函数、勾股定理等知识.从能力层面看，此题主要考查学生的经验迁移能力、构图能力和逻辑推理能力.因此本题的解决最关键的是对题目的分析.首先，思考条件是什么，从条件本身到条件重组思考定的数量有哪些，量与量之间存在定的位置、数量关系有哪些，即研究条件得什么，明确定的元素和定的关系有哪些.其次，研究问题是什么，将问题放在局部或整体进行思考，尤其要明确问题的属性，图7比如BC是什么？是弦就要基于圆的性质研究BC、是三角形的一边就要基于三角形研究BC，即研究边与边、边与角的关系，化归解三角形，通过化斜为直，建立三角函数进行解决问题，同时思考问题解决需要定什么.最终，基于条件、问题、定的元素思考与本题相关的解决方法、经验、模型，最终确定解题策略.基于“波利亚解题原理”发现迁移经验的思维导图如图7所示.

3.2 强化学生注重方法、经验、模型的积累

罗增儒教授曾说过：“从思维的角度看，模式识别的解题策略体现思维定势正迁移的积极作用.‘遇新思陈，推陈出新就是为了在当前问题与头脑中已有的知识、经验之间建立联系，以诱发积极有用的思维定势.”所以，积累、甚至记忆一些“模型”是必须的.尤其是解决此题需借助解三角形与定角轨迹此类模型的相关方法和经验，特别需要用基本图形经验、思维经验相结合.如果学生从来没有体验过，那么解决这个问题还是很困难的.因此问题的解决关键环节是在研究条件与问题后思考与其关联的经验有哪些.比如本题：经验一，研究线段的长度，通常转化为轨迹问题，最终研究点与点的距离问题，也或是建立函数关系由自变量的取值范围研究应变量的范围;经验二，定弦定角应该自然想到定角轨迹;经验三，研究三角形的边的长度，通常化归解三角形，建立三角关系把角与边相关联.这些模型、经验、方法平时在解题中要不断渗透，通常经历：解一类题归纳提炼——尝试应用感悟理解——再提炼把一系列题目串联三个阶段.

3.3 增强学生经历特殊到一般的意识

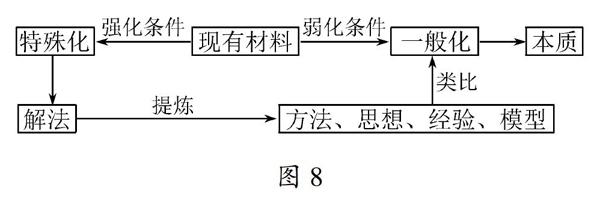
将原问题特殊化或一般化进行的变式，因为特殊则解法便于发现，再提炼特殊化的解法，用于解决原问题和一般化的问题.当问题趋于一般化时，最后留下来就是问题的本质，比如本问题，当∠C为m°时，BC的长度范围是不确定的，基于原问题解决的经验，本题意在引导学生经历特殊到一般的认识，从而对此类问题的本质就明晰了.通过本题变式与解法发现基于“从特殊到一般”探本质、寻通法的思维导图如图8所示.

因此，问题的解决有必要引导学生思考问题能否一般化和特殊化？控制变量强化条件或弱化条件使得原问题特殊化与一般化.在特殊化后思考解法，提炼基本图形、方法、思想、经验、模型等等，并将其所有类比迁移到原问题和一般化的问题.

3.4 给予学生多一点尝试与感悟的机会

英国心理学家莱士的研究表明，解决问题要经历准备、孕育、明朗和验证这四个阶段.因此，问题的解决需要平时在教学的过程中多一些孕育的过程，有必要给学生多一点尝试与感悟的机会，在此过程中需要教师精心设问.对于较难题或陌生题绝对不是简单给思路与解法，一定需要老师站在高处，层层设问，学生经历感悟理解，以本题为例.

轨迹的视角：探索轨迹，基于临界确定范围.设问如下：

问题1：作一个满足条件的△ABC.

问题2：满足条件的三角形有多少个，为什么？请作出所有满足条件的点C.

问题3：思考BC是什么？

问题4：改变题目的条件，能更加一般化吗？原问题与变式后的问题有何内在联系？

设计意图 从特殊到一般，从有限到无限，从存在到合理，从感知到明晰，步步推进.学生经历感悟、理解、归纳、应用的过程.不仅思考定与变，还需要思考与其关联的经验、方法、模型等，最终再归纳提炼方法、经验、模型.问题3研究问题是什么，不同的属性带来不同的方法与经验.

函数的视角：建立关系，基于范围寻求范围.设问如下：

问题1：思考BC是什么？

问题2：与BC相关的量有哪些，有何关系？

问题3：如何求BC的长度？

問题4：改变题目的条件，能更加一般化吗？原问题与变式后的问题有何内在联系？

设计意图 从BC的属性出发，研究BC是什么，通过控制变量的视角将问题进行变换，再与已有条件，特别是定的量与定的关系相关联，最终用函数的视角解决问题.

问题个数是无限的，但是问题解决的方法是有限的，如何用有限的方法去解决无限多的问题，就要我们分析定与变，对于变要建立关联，再用定的量与定的关系进行刻画，当我们还未有清晰的思路，一定要寻问自己基于不同的属性追问问题是什么.当然，最终问题的解决不仅仅靠分析条件与问题，还需要将积累的方法、经验、模型与分析的进行嫁接，这种能力需要平时教学过程中给学生足够的感悟理解的空间.