爆炸荷载结构等效静载动力系数研究
2019-11-05耿少波葛培杰李洪徐鹏
耿少波,葛培杰,李洪,徐鹏
(1.中北大学 理学院,山西 太原 030051;2.大连理工大学 水利工程学院,辽宁 大连 116024)
0 引言
易爆物品生产运输储藏不当、恐怖袭击及敌方军事行动等原因均会产生化学爆炸,对建筑结构产生冲击波荷载,致使结构损伤及破坏,引发人员伤亡。典型破坏案例如美国“911”事件中双子塔的倒塌、2013年连霍高速公路义昌大桥因危险品运输发生爆炸倒塌、2015年天津滨海新区物流仓库爆炸致使大范围建筑受损、2017年宁波江北区附近多幢民用房屋因煤气爆炸倒塌。建筑物抗爆设防为避免爆炸冲击波损失的一种重要手段,我国国家标准GB 50038—2005人民防空地下室设计规范及2012年新订的国家标准GB50009—2012建筑结构荷载规范等标准中包含爆炸作用计算,并将爆炸荷载简化为只包含正超压的三角形衰减荷载,即荷载模式为等冲量线性模式。对绝大多数建筑而言,基于弹性理论的结构防爆设计会导致制造成本偏高,基于延性比的弹塑性状态设计可为结构抗爆提供不同层次的选择。将爆炸动载转换为基于动力系数的等效静载,可使爆炸作用计算更为简便[1-2]。
因此,国内外学者对结构爆炸荷载等效计算方法开展了大量研究工作。Biggs[3]最早对线性衰减荷载进行等效静载分析,适用于爆炸荷载的近似简化;方秦等[4]研究了横向爆炸作用下柱的受迫振动,提供了等效静载分析基础;Baker[5]指出空气介质中化学爆炸冲击波呈指数型衰减,等冲量计算按此计算较准确;张晓伟等[6]分析了爆炸作用下混凝土板的荷载等效方法,采用量纲分析法分析了三角脉冲荷载与等效荷载之间的关系;任秀敏[7]采用冲击荷载等效静载法分析了雷达天线罩的动位移;杨科之等[8-9]研究了线性衰减荷载等效静载法作用下结构弹塑性阶段动力系数与延性比的关系,指出延性比较大时动力系数无解;伍俊等[10]采用爆炸荷载线性衰减模式进行防爆墙结构分析,指出等效荷载分析的可行性;颜海春等[11]采用爆炸荷载等效静载对人防工程封堵梁进行内力分析,但未指出结构延性比与荷载动力系数之间的关系;杨涛春等[12]采用爆炸荷载线性衰减模式对钢筋与混凝土组合梁进行了等效静载与有限元分析对比计算,明确了等效静载具有足够精度;陈俊杰等[13]研究了爆炸荷载冲量简化分析方法,其荷载形式为线性衰减荷载模式;Chen等[14]采用线性等效荷载分析了地下拱结构- 土体爆炸耦合效应,指出了冲击波等效单自由度的有效性及方便性;Shi等[15]指出了指数型函数进行爆炸荷载冲量及等效静载时会更准确;Gantes等[16]计算了指数型爆炸荷载单自由度结构的弹塑性位移解,但未对结构延性比、动力系数深入分析;Louca等[17]在分析爆炸作用时也指出爆炸衰减荷载采用指数型函数会更接近冲击波实测结果。
另外,基于延性比的弹塑性阶段动力系数计算与荷载作用时长紧密相关,等冲量线性衰减荷载模式正超压等效时长小于真实爆炸荷载作用时长,会影响结构塑性位移响应,进而对其动力系数产生什么差异、对抗爆设计有何影响,国内外学者鲜有研究。
故本文选取目前抗爆设计规范推荐采用的等冲量线性衰减荷载模式与较精准描述爆炸荷载的指数型衰减荷载模式为分析类型,分别进行弹塑性动力系数表达式推导及对比,进而确定爆炸荷载等峰值、等冲量而衰减函数不同对等效静载动力系数的影响程度。
1 弹塑性体系动力微分方程
1.1 等效单自由度微分方程
根据结构动力学等效单自由度弹性理论及达朗贝尔原理,弹性响应阶段微分方程为
(1)
式中:kM-L为弹性等效质量- 等效荷载系数比;m为结构单位长度质量;l为结构长度;W(t)为结构动位移;K为结构等效弹簧系数;Δp(t)为爆炸荷载时程函数。
设结构弹性位移达到最大值WT时,结构振动速度为vT,此时刻tT为结构进入塑性振动的区分点,此后结构弹塑性阶段微分方程为
(2)
式中:km-l为塑性等效质量- 等效荷载系数比;qm为结构塑性阶段抗力。
若采用等冲量线性衰减荷载模式,则函数为
(3)
若采用指数型衰减荷载模式,则函数为
(4)
式中:Δpm为超压峰值;f(t)为荷载归一化衰减函数;a为指数型荷载模式形状参数;ti为等冲量线性衰减荷载等效作用时长;t+为指数型衰减荷载正超压真实时长,如图1所示。

图1 荷载类型及作用时长示意图Fig.1 Schematic diagram of two load types and load durations
由(1)式及Duhamel积分可知

(5)
(6)
式中:Wcm为静载Δpm作用下结构的静位移;K(t)为结构振动动力系数;ω为结构自振频率;τ为时间参数。
弹性阶段结束时,对应的位移及速度分别为
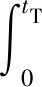
(7)

(8)
由(2)式、(7)式及(8)式可知塑性阶段结构振动位移及速度分别为
(9)

(10)
考察的是结构弹塑性阶段内的等效静载,即其抗力动力系数为
(11)
1.2 荷载等效时长与作用时长
根据爆炸荷载作用时长t+、爆炸荷载超压峰值Δpm及指数函数曲线形状调整参数a,由冲量的定义及(4)式可知,对于指数型衰减荷载,其冲量为
(12)
对于等冲量线性衰减荷载,其冲量为
(13)
因此令(12)式与(13)式冲量相等,则等冲量线性衰减荷载的等效时间为
(14)
参数a越大其函数在负超压数值越小甚至为0,因此在超压曲线拟合时,为了能较准确地拟合正超压和负超压的正常形态,一般情况1.27≤a≤1.61[18],若取其端点及中值进分析,则指数型爆炸荷载作用时长与线性等效荷载等效时长比值如表1所示。

表1 作用时长比值表
2 结构弹塑性阶段划分
化学爆炸冲击波荷载正超压作用时长t+很小,小于结构出现最大动位移反应时间[5],对应的等效冲量换算时长ti更短,结构完成塑性最大变形时间tm>t+或tm>ti,且此时结构外荷载Δpmf(t)为0;结构达到弹性阶段最大位移继而进入塑性阶段的时刻tT就存在两种可能:一种是ti 若令θT=ωtT、θi=ωti、θ+=ωt+,则由(7)式可知,对于等冲量线性衰减荷载及其等效时长,确定其动力系数为 (15) 对于指数型衰减荷载及其对应作用时长,经过多次分部积分,其动力系数为 (16) (17) 若定义(16)式为Kh=sinθT×A*+cosθT×B*,即 则A*、B*代替(17)式中参数A、B可得指数型衰减荷载cosθT表达式,且可得 (18) 由(8)式可得等冲量线性衰减荷载弹性阶段结束时对应的振动速度及比值分别为 vT=Wcm[cosθT-cos (θT-θi)+θisinθT]/ti, (19) (20) 同理,可得指数型衰减荷载相应比值为 (21) 式中:C*、D*表达式分别为 由(9)式及塑性阶段v(tm)=0可导出 (22) 由(10)式及塑性阶段v(tm)=0可导出 (23) (22)式代入(23)式,可知 (24) 且 (25) (22)式、(23)式及(20)式代入(24)式,可得等冲量线性衰减荷载延性比为 (26) 同理可得指数型衰减荷载延性比为 (27) 据此,基于延性比β、自振周期与荷载作用时长乘积ωti或ωt+,便可计算出等冲量线性衰减荷载与指数型衰减荷载相应的动力系数。 若再令θm=ωtm,由前述定义可知θT<θi<θm或θT<θ+<θm,由动力系数定义及(7)式可知,对于等冲量线性衰减荷载,可计算出其动力系数 (28) 同理,对于指数型衰减荷载,经过积分后其动力系数为 (29) 由(8)式可得等冲量线性衰减荷载弹性阶段结束时对应的振动速度及比值分别为 vT=Wcm[-1+cosθT+θisinθT]/ti, (30) (31) 同理,指数型衰减荷载相应比值为 (32) 由(9)式及塑性阶段v(tm)为0可知,对于等冲量线性衰减荷载,振动速度为 (33) 同理,对于指数型衰减荷载积分后,振动速度为 (34) 由(31)式及(33)式求解出等冲量线性衰减荷载对应参数为 (35) 由(32)式及(34)式求解出等冲量线性衰减荷载对应参数为 (36) 由(10)式可得等冲量线性衰减荷载延性比及指数型衰减荷载函数延性比分别为 (37) (38) 由于动力系数Kh计算公式不是关于延性比β的显式函数,计算参数θT、θi或θ+、θm根据较晚或较早进入弹塑性公式(26)式、(27)式及(37)式、(38)式编程,由其定义及延性比β的范围作为控制条件,然后由初值赋值后迭代求解。 根据表1参数a取值范围、等冲量线性衰减荷载等效时间ti与爆炸荷载正超压作用时间t+对应关系,取ti与t+比值1.464为工况1,取比值1.532为工况2,取比值1.600为工况3,进行动力系数分析。为独立分析及相互对比,3种工况均取ωti(即θi)为0.2~2.8,步长为0.2,共计14项,ωt+(即θ+)按作用时长与等效时长换算后,分别考察不同延性比β下的数值。为能涵盖工程结构设计时所对应的延性比,采用延性比为1~5不等间距的范围作为计算示例,计算结果如表2~表4所示。表2~表4中:1)波浪线形成的左侧(右侧)数据为指数型衰减荷载模式结构较晚(较早)进入塑性阶段所对应的推导公式计算得出;2)虚线左上方(右下方)数据为等冲量线性衰减荷载模式结构较晚(较早)进入塑性阶段所对应计算公式得出;3)为精简篇幅及数据对比,等冲量线性衰减荷载计算结果不再单独给出,以其相对指数型衰减荷载计算结果的偏差比例表示(括号内),未以百分比标注的数据代表等冲量线性衰减荷载模式下无解。 整体上来看,表2~表4中β=1.0对应的弹性状态设计较β>1.0对应的弹塑性状态设计对应的等效静载动力系数要高很多,即建筑结构按照弹性设计的工程造价会增加;且各状态下θ+(ωt+)数值增大,动力系数变大,考虑到建筑结构需承受的爆炸荷载的不确定性,即爆炸作用时间t+无法有效控制,较为有效的结构力学措施为降低结构自振频率ω数值,选用刚度较小的力学模式。 表2 工况1下动力系数Kh计算 表3 工况2下动力系数Kh计算 指数型衰减荷载的弹塑性阶段动力系数(β>1.0)由2条折线划分为3块区域,等冲量线性衰减荷载的弹塑性阶段动力系数则划分为两块区域。等冲量线性衰减荷载的可设计范围较小,当延性比β≤3.0时,约为指数型衰减荷载可设计范围的78%;当β=5.0时,降低至54%,缩小的范围均在θ+较大区域,即对刚度较大的结构能否顺利设计影响较大。 表4 工况3下动力系数Kh计算 当θ+>2.0(约θi>1.4)时,随着设计延性比β的降低,动力系数逐步提高,指数型衰减荷载可实现设计状态上从较早进入塑性阶段到较晚进入塑性阶段、再到进入弹性状态的设计思路,体现了抗爆设计不同层次与结构弹塑性响应的一一对应关系,而线性衰减荷载在此区域尚不能完整地显示此特征。 曲线形状调整参数a越大,指数函数曲率越大,从本文计算工况来看:对θ+<1.0的所有β取值均不产生影响;对θ+>1.0且弹性状态及较晚进入弹塑性状态的动力系数产生降低作用;对θ+>1.0且较早进入塑性状态的动力系数产生提高作用,工况3比工况1提高最大幅值为14.9%,工况3比工况2提高最大幅值为6.1%. 从表2~表4中可以看出,误差主要集中在2%~11.5%之间,即以等冲量线性衰减荷载模式计算结果偏大为主。当延性比β<1.8时:工况1中由等冲量线性衰减荷载计算的动力系数均高于指数型衰减荷载计算数值,平均高出3.9%,最高数值为13.4%;工况2平均高出4.3%,最高数值为14.5%;工况3平均高出5.1%,最高数值为15.9%,说明在较低延性比β抗爆设计下,按等冲量线性衰减荷载计算其等效静载时取值偏高,对结构设计偏安全。 当延性比β>2.0时,较大θi对应的动力系数在3种工况中,由等冲量线性衰减荷载计算的数值均小于按指数型衰减荷载计算数值的情况,低于的幅度最高分别为16%、11%及16%,即抗爆规范推荐的等冲量线性衰减荷载模式偏不安全。 本文以爆炸荷载作用下结构等效静载动力系数为研究对象,分析了线性与指数型两种函数作为爆炸冲击波衰减荷载模式下的弹性、弹塑性阶段等效静载动力系数差异。主要得出以下结论: 1)两种荷载模式的动力系数在弹性阶段、较晚与较早进入弹塑性阶段衔接处均能较好衔接,采用基于延性比的弹塑性设计具有明显的经济意义。 2)在延性比β<2.0对应的可设计范围内,指数型衰减荷载动力系数低于等冲量线性相应数值,差异比例较低。 3)曲线形状调整参数a越大,对θ+>1.0且较早进入塑性状态的动力系数会产生提高作用,此区间内抗爆设计时采用指数型衰减荷载较安全可靠。 4)当设计延性比β>3时,若θ+<1.6(即约θi<1.0),采用线性或指数性衰减荷载均可,若θ+>1.6(即约θi>1.0),应采用指数型衰减荷载模式计算模式的动力系数。2.1 结构较晚进入塑性阶段





2.2 结构较早进入塑性阶段
3 动力系数计算算例
3.1 计算工况
3.2 结果分析与讨论

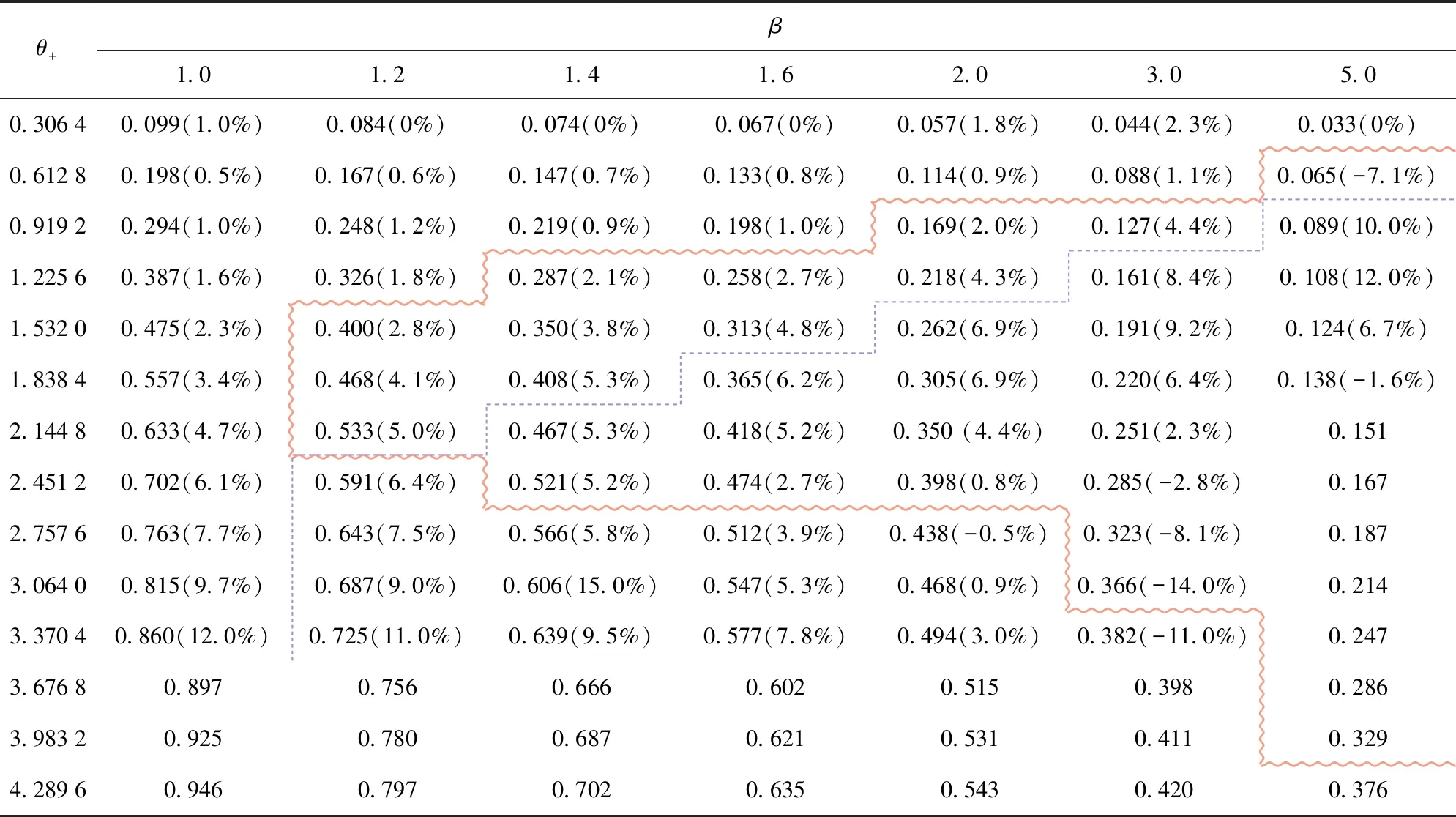
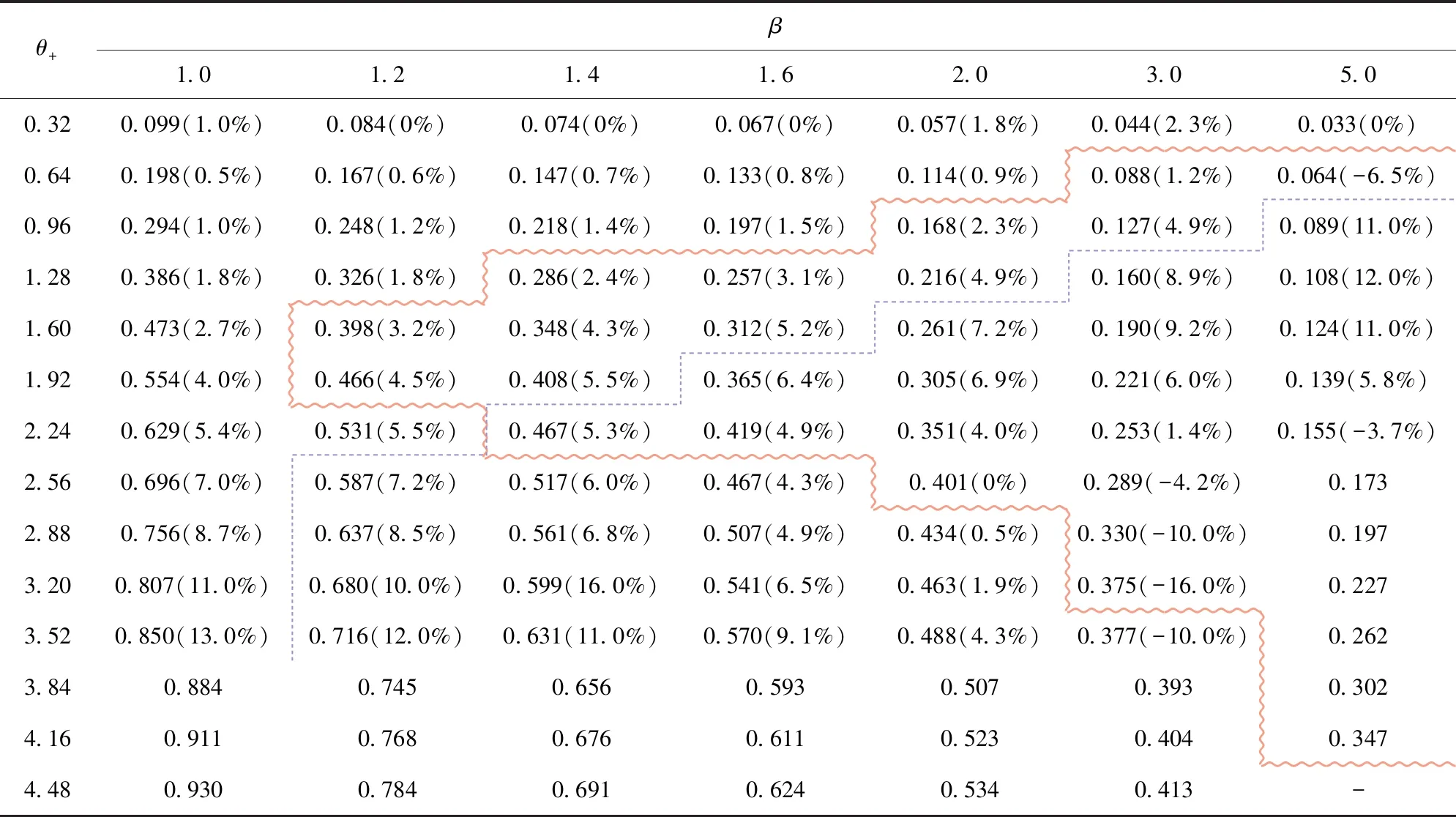
4 结论
