陈义学，张 斌

(华北电力大学 核科学与工程学院，北京 102206)

粒子输运计算在许多领域起到至关重要的作用，如核装置的屏蔽设计[1]、聚变中子学、辐射治疗应用[2]和天体物理等。随着计算机软件和硬件技术的快速发展，粒子输运模拟逐渐成为研究科学问题的重要手段。在屏蔽计算方面，辐射屏蔽安全是核能安全的重要组成部分，输运计算方法的研究为辐射屏蔽设计提供有力支撑。稳态中子输运方程是一个包含能量、空间和角度变量的六维方程[3-4]，同时由于实际屏蔽模型几何材料的复杂性和非均匀性，三维大规模高保真粒子输运模拟极具挑战。目前的屏蔽计算由于计算条件和计算时间的限制，在物理和几何方面采用了大量近似处理，实际经验可以修正近似引入的不确定性。然而，不同屏蔽问题的特性差异较大，已有的屏蔽计算经验适应性不强。随着核能技术的发展，一些复杂屏蔽输运问题的出现，如孔道屏蔽问题[5]、聚变堆深穿透问题、医学物理等，传统屏蔽计算方法存在局限性，导致屏蔽计算的精度和速度均受到极大影响。

离散纵标法(SN)具有计算速度较快、精度较高、适合求解深穿透输运问题等优点，在屏蔽计算中得到广泛应用。SN对输运方程的方向变量采用直接离散的方式，将原来连续的方向变量转换为有限的离散方向求解。在角通量密度各向异性较强的物理模型中，当离散求积组数值积分角通量密度精度较低时，会导致射线效应问题[6-8]，使标通量密度呈现空间震荡如锯齿波纹状分布。射线效应极大影响了屏蔽计算的精度及辐射屏蔽设计的可靠性。对于具有孤立点源、大空腔或孔道的屏蔽问题，射线效应更加严重，因此有必要研究精确、可靠的屏蔽计算方法。实际屏蔽计算模型中输运方程变量的离散导致极大的耦合线性方程组，在计算机存储和快速求解方面都存在挑战，这是粒子输运模拟的难点。为有效地利用计算资源，本文采用角度自适应方法求解输运问题[9-11]。

1 自适应离散求积组

自适应方法根据计算过程中处理数据的特征自动调整求解参数，是求解偏微分方程的一种方法。数值求解过程中自动调整计算所需网格，产生最佳的离散方式，从而以尽量少的计算量达到要求的精度。角度自适应方法基于角度变量的局部细化[12-14]，采用相对于均匀角度离散较少的离散方向，有效地提高屏蔽计算精度。自适应方法成功应用的关键因素有：可靠的局部误差估计，用以评价局部区域的离散误差；灵活的数据结构，便于程序实现与应用；不同细化层之间的数据传递的延拓和限制算子。

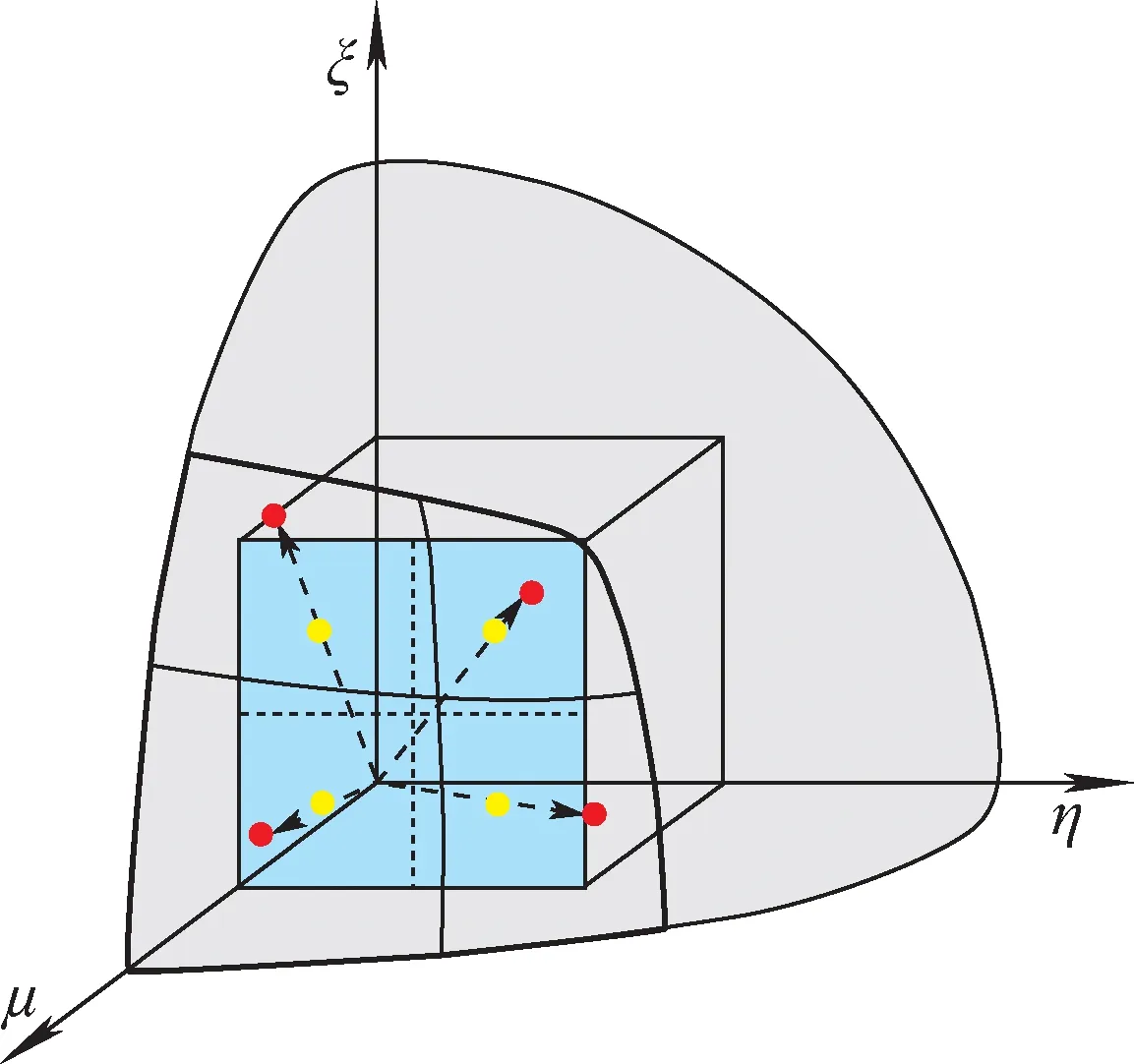
图1 立方体的外接圆Fig.1 Cube inscribed into unit sphere

实际屏蔽计算问题中，在局部角度区域内经常出现角通量密度间断或接近间断的情况，自适应离散求积组应具备在较小的角度区域内精确计算通量矩的能力，同时还需要具有局部角度区域可细化、权重系数非负和离散方向数不受限制等特征。自适应离散求积组的构造，将1个立方体镶嵌到单位球内，立方体的每个角对应每个卦限，如图1所示。在立方体表面上划分出若干四边形，在每个四边形内定义离散方向，向单位球面投影得到求积点，通过细化四边形的划分来细化离散方向。每个平面四边形包含4个坐标点，从单位球的原点到每个坐标点的矢量确定唯一的离散方向，每个球面四边形内对应有4个离散方向。采用中心点法确定坐标点，平面四边形内4个子四边形各自的中点作为坐标点。求积组的所有离散方向确定后，每个平面四边形对应的球面四边形的面积作为该求积点的权重系数。

任意局部角度区域的细化功能是自适应离散求积组的优点之一，当角通量密度在局部角度区域内不光滑，甚至出现间断或接近间断的情况时，在局部角度区域内细化离散方向，局部细化的求积组具有分层的数据结构。1个卦限对应的3个四边形上分别采用二阶、三阶和四阶细化求积组的情况，如图2所示。

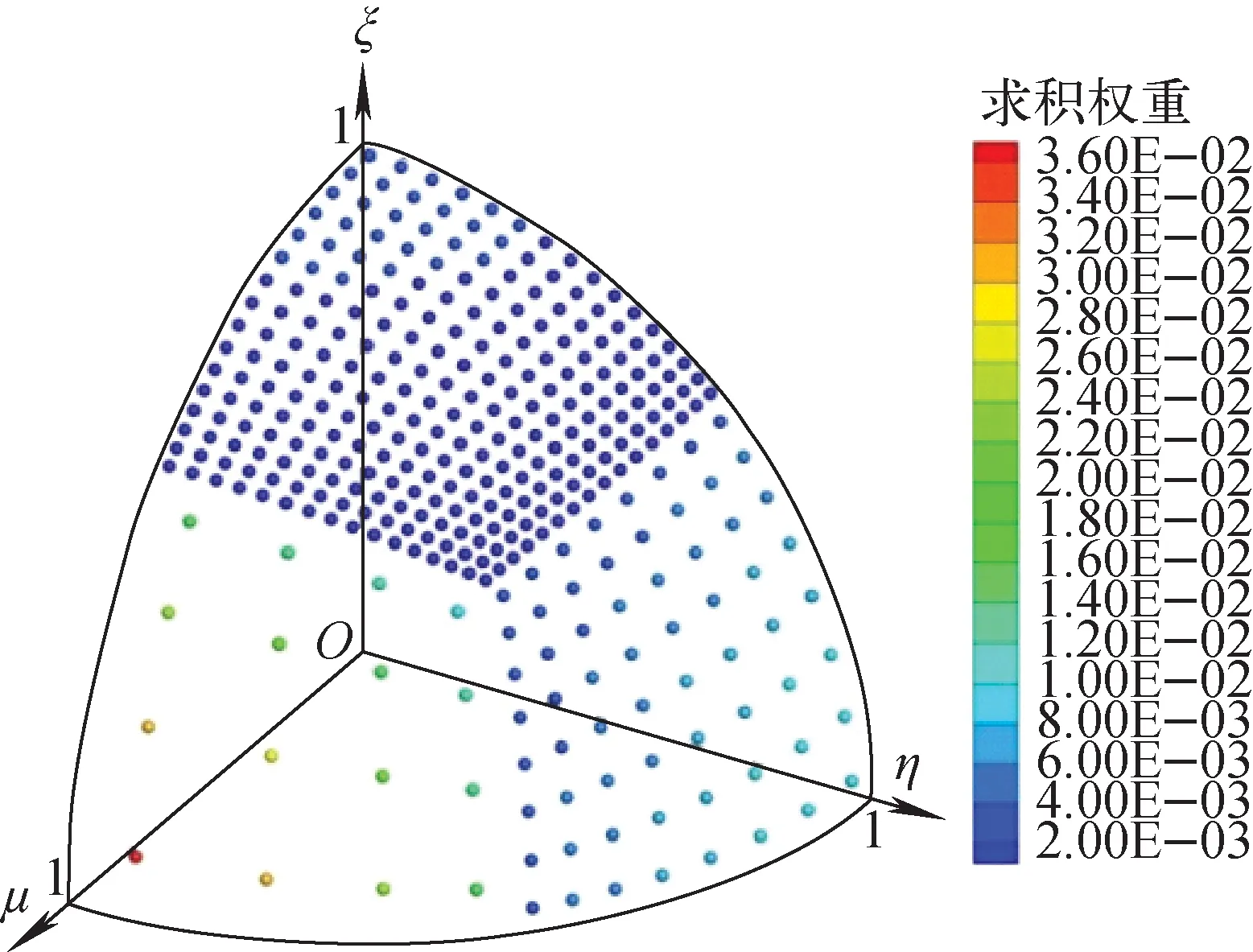
图2 局部区域细化求积组Fig.2 Local quadrature set refinement

2 角度自适应方法

角度自适应方法在角通量密度梯度较大或间断的区域进行局部细化，能提供较好的数值近似。另一方面在角通量密度分布光滑的区域，采用较粗的角度离散仍能产生精确的计算结果。自适应方法不仅可有效控制离散误差，且极大减少了计算量。屏蔽计算问题的几何模型划分为不同的求积区域，1个区域内的所有网格采用相同的求积组，分别定义每个求积区域的求积组。自适应过程中还需要定义一些常数，包括第1次自适应前的迭代次数、两次自适应间的迭代次数、最大自适应次数和自适应收敛准则等。在稳态输运问题的计算中，角度自适应方法以初始求积组开始输运扫描，所有求积区域采用相同的低阶求积组。经历若干次源迭代后，基于当前的数值解获得角度离散误差分布。在此过程中需准确估计误差分布，将其中一部分误差相对较大的角度离散区域细化，即采用更高阶求积组代替当前的低阶求积组，尽可能地减少离散角度未知量的个数。然后，将该细化的求积组作为新的计算参数，在下一次自适应前一直使用。每经历多次迭代后进行1次自适应判断，自适应过程一直持续到满足规定的误差收敛准则或达到最大迭代次数。角度自适应方法流程如图3所示。其中Na为自适应过程对应的内迭代次数，为提前设置的1组常数，Np为第1次自适应前的内迭代次数，为提前确定的1个常数。

图3 角度自适应方法流程图Fig.3 Flow chart of angular adaptive algorithm

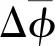
(1)

(2)

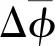
若求积区域边界上任何一个网格的角度离散误差大于事先规定的自适应细化收敛准则，则该求积区域的求积组细化到下一层高阶求积组，同时更新该求积区域网格上的通量矩和区域边界的出射角通量密度。自适应细化判断如下：

(3)

(4)

式中：εflux为标通量密度自适应细化收敛准则；εcurrent为中子流密度自适应细化收敛准则。

通过当前数值求解的后验误差估计得到局部角度离散误差，为角度自适应方法提供了判断依据。角度自适应可采用4种尺度，包括全部求积区域统一自适应、各求积区域独立自适应、各求积区域的每个卦限独立自适应和各求积区域每个球面四边形独立自适应。另外，由于输运方程空间角度的强耦合性，空间变量的离散方式和空间网格划分都会对角度自适应过程产生影响。相邻求积区域如果具有相同的离散求积点，一对一的简单映射可传递相邻求积区域的角通量密度。若相邻求积区域的离散求积点存在不同的离散方向数目和不同的离散方向位置，简单一对一的映射无法处理，角通量密度在一个求积区域传递到另一个求积区域需要映射方法。对于角通量密度从高阶求积组映射到低阶求积组的情况，一般采用多项式权重法，即通过4个与待求方向大圆距离最近的高阶求积组的离散点，计算1个低阶求积组离散点的角通量密度；对于从低阶求积组映射到高阶求积组的情况，则采用球谐函数拟合法，将角通量密度球谐函数展开并进行传递。

基于后验误差估计的角度自适应方法能自动优化角度离散，同时有效地控制全局通量密度的计算误差，然而通常实际工程计算中感兴趣的物理参数由局部或全局通量密度函数的积分确定，如核反应堆设计中功率密度分布、泄漏率和有效增殖因数等，辐射屏蔽计算中剂量当量率和探测器响应等，医学物理应用中特定器官的剂量率等。从工程角度出发，获得所有网格的精确解并没有必要。在某些屏蔽计算问题中，数值结果在整个模型内相差多个数量级，在某区域的绝对误差可能很小，但相对误差可能会很大。在源区和源区与屏蔽材料的交界面处数值结果较大，自适应方法容易使该区域变量的离散过于细化，造成关注的屏蔽区域相对误差依然很大。因此，关于特定物理量的误差估计与现实应用更加相关，根据用户的定义确定目标导向自适应方法中的目标函数，同时作为输运共轭方程的源项，产生相对于目标函数的误差估计。

3 理论方法测试与分析

图4 Kobayashi基准题模型2Fig.4 Model 2 of Kobayashi benchmark

Kobayashi基准题模型2的几何如图4所示，该基准题模型对传统确定论输运方法提出了挑战，是典型的深穿透屏蔽问题[15]。孔道的存在增加了角通量密度的各向异性程度，采用低阶求积组时，导致较大的角度离散误差。本文分析角度自适应方法的精度和效率，并研究关键参数的选择对自适应方法的影响。

图5示出均匀细化、角度自适应和目标导向自适应方法关键点相对误差均方根的变化。由图5可见，随离散角度数的增多，相对误差逐渐减小。角度自适应过程中，由于映射方法精度的影响会造成曲线在某些区域产生震荡。在满足精度要求的前提下，角度自适应和目标导向自适应方法均能有效地减少角度变量的数目。目标导向自适应方法仅采用52个卦限平均离散角度数就可获得较高的计算精度。当所需精度均方根为1.00×10-2时，角度自适应方法需要的每个卦限平均离散角度数约为250个，而均匀细化方法的要超过3 000个。目标导向自适应方法仅是均匀细化方法离散角度数的1/60，极大地减少了计算量。角度自适应和目标导向自适应方法的计算时间分别为354 s和83 s。目标函数作为输运共轭方程的源项，局部角度离散误差通过对计算目标函数的重要性加权，产生适当的目标导向的误差估计，生成针对特定目标函数精度改善最有效的离散角度分布。二阶均匀细化求积组和目标导向自适应方法的相对误差列于表1，二阶均匀细化求积组的平均卦限离散方向数为48个，目标导向自适应方法仅增加了4个离散角度，计算精度获得很大提高，相对误差的均方根从1.86×10-1下降到1.19×10-2。

图5 模型2关键点相对误差的均方根变化Fig.5 RMS variation of relative error of key point in model 2

表1 模型2关键点通量密度的相对误差Table 1 Relative error of key point of flux density for model 2

4 结论与展望

基于价值理论的目标导向方法与角度自适应相结合，有效地减弱了角度离散误差对屏蔽计算的影响，提高了屏蔽计算方法的精度和效率。自适应求积组具有较好的收敛性，积分精度满足输运计算的要求。对于Kobayashi基准题模型，自适应方法比均匀细化离散角度数少1～2个数量级获得了相同的计算精度，极大地减少了计算量。为进一步提高数值积分效率和精度，研究间断有限元自适应离散求积组。空间和角度耦合的自适应方法研究是未来的一个难点，其中后验误差估计是极具挑战的问题。