随机分数阶非线性系统解的存在唯一性
2019-10-16马海云
马海云,吕 文
(烟台大学数学与信息科学学院, 山东 烟台 264005)
微分方程作为描述物体的随机动态模型已被广泛应用于化学、物理、生物工程和金融等多个领域. 例如, 通过建立标准维纳过程, 以此为特征来描述随机环境波动的影响. 基于动态建模的发展, 并将环境波动方面纳入微分方程所描述的数学模型中, 将经典的数学建模方法与随机模型相结合, 已被用于股票价格的随机动态模型. 而且随着科学的发展, 我们对随机分数阶微分方程有了越来越深的认识. 分数阶微分方程非常适合于刻画具有记忆和遗传性质的材料和过程, 在电极电介质极化[1]、 电路[2]、电磁波[3]等领域中有很重要的应用. 在此背景下, 文献[4]通过引入在线性无关时间尺度下运行的动态过程的概念, 用随机微分方程组描述了动态过程的数学模型, 研究了形如
dx=f(t,x)dt+g1(x,t)dB(t)+
(1)
的随机分数阶微分方程解的存在唯一性问题, 并提出了求解多时间尺度下线性和非线性标量随机微分方程的闭式解的方法, 最后将结果应用于多时间尺度下种群生态和流行病过程的研究.
另一方面由布朗运动驱动的随机微分方程被广泛用于描述具有随机扰动的系统. 但在对工程的实际应用中, 存在着某些局限性. 例如, 在具有功率噪声滤波器的电路系统中, 用静止过程来描述随机扰动对其他电元素的最终影响比用白噪声来描述更加合理. 在此背景下, 文献[5]研究了形如
dx=f(x,t)dt+g(x,t)ξ(t)dt,x(t0)=x0(2)
的随机非线性系统, 其中ξ(t)是一个二阶矩过程. 在系数分别满足Lipschitz条件和局部Lipschitz条件下给出了系统解的存在唯一性定理, 同时给出了噪声到状态p阶矩稳定性和噪声到状态依概率稳定性的概念, 并研究了系统的渐进增益特性. 此外, 文献[6]研究了形如
dx(t)=fσ(x(t),t)dt+
gσ(x(t),t)ξ(t)dt,x(t0)=x0
(3)
的随机切换系统, 给出了噪声到状态的指数稳定性.文献[7]则利用Lynapunov函数给出了随机切换系统全局解的存在性和噪声到状态稳定性的判据.
受以上文献的启发, 本文研究形如
dx=f(x,t)dt+g1(x,t)ξ(t)dt+
g2(x,t)(dt)α,x(t0)=x0
(4)
的随机分数阶非线性系统, 在Lipschitz条件和线性增长条件下, 给出了系统解的存在唯一性定理.
本文第1节中引入随机分数阶非线性系统的若干基本概念. 第2节中, 将在对过程ξ(t)的两类假设下分别给出二阶矩过程驱动的随机分数阶非线性系统解的存在唯一性定理.
1 基础知识
首先给出分数阶积、微分运算的一些基本概念, 详细内容参见文献[8-9].
定义1(Riemann-Liouville分数阶积分) 设0<α<1 且f∈L1[a,b], 其中L1[a,b]=L1[[a,b],n]={y|y:[a,b]→n且y是勒贝格可积的}.则对所有t∈(a,b), Riemann-Liouville 左、右α阶分数阶积分分别定义为
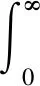
定义2(Riemann-Liouville分数阶导数) 设0<α<1,f是定义在区间[a,b] 上的绝对连续函数, 则对所有t∈(a,b), Riemann-Liouville 左、右α阶分数阶导数分别定义为


定义3(多时间尺度积分) 对于p∈,p>1, 设{T1,T2,…,Tp}是一组线性无关的时间尺度. 设f:[a,b)×p-1→n是一个连续函数, 定义f(t) 为f(t)=f(T1(t),T2(t),…,Tp(t)),复合函数f在区间 [t0,t]⊆(a,b) 上的多时间尺度积分定义为p积分与时间尺度T1,T2,…,Tp的总和, 用If表示, 即
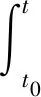
定义4(多时间尺度微分) 设f是多时间尺度积分中定义的函数, 复合函数f的多时间尺度微分定义为f相对于时间尺度T1(t),T2(t),…,Tp(t)的偏微分的和, 用df表示, 即
其中(djf)(t)=f(T1(t),…,Tj-1(t),Tj(t+Δt),Tj+1(t),…,Tp(t))-f(T1(t),…,Tj-1(t),Tj(t),Tj+1(t),…,Tp(t)),j=1,2,…,p.对于小的Δt, Δt≈dt, 且(djf)(t)对应于定义3中积分中的(Ijf)(t).
引理1[10]设f(t) 是一个连续函数, 则分数阶微分方程:
dx=f(t)(dt)α,t≥0,x(0)=x0,0<α≤1
的解为

给定一个完备的概率空间(Ω,F,Ft,P), 信息族Ft满足通常条件, 即, 它是递增和右连续的, 并且F0包含所有P-零集.对任意给定的T>t0≥0, 考虑由以下方程描述的随机分数阶非线性系统
dx=f(x,t)dt+g1(x,t)ξ(t)dt+
g2(x,t)(dt)α,x(t0)=x0,
(5)
(A1): |f(x,t)-f(y,t)|+|g1(x,t)-g1(y,t)|+|g2(x,t)-g2(y,t)|≤ L|x-y|.
(A2): |f(x,t)|2+|g1(x,t)|2+|g2(x,t)|2≤ K(1+|x|2).
由引理1知, 方程(5)可以写成以下等价形式

(6)
定义5 称随机过程x(t) 是系统(6)的一个解, 如果x(t) 满足:
(1)对所有的t∈ [t0,T], x(t) 是连续的;
(2)x(t) 为 Ft-适应的;
(3)对所有 t∈[t0,T], 方程(6)成立.
2 解的存在唯一性
在本节中, 将在对过程ξ(t)的两类假设下分别给出系统(6)的解的存在唯一性. 首先给出以下假设.
(A3): 过程ξ(t) 是Ft-适应且分段连续的, 存在参数c0,d0>0, 使得对∀t≥ t0, 有
E|ξ(t)|2≤d0ec0t.
定理1 若假设(A1)、(A2)和(A3)成立, 则系统(6)在[t0,T] 上存在唯一解x(t).
证明存在性.设x(0)(t)=x0, 令
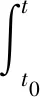

由初等不等式(a+b+c)2≤3(a2+b2+c2)和施瓦兹不等式得
E|x(1)(t)-x(0)(t)|2=





(7)

进一步地, 令
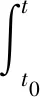


由施瓦兹不等式及(A1), 得
E|x(k+1)(t)-x(k)(t)|2≤



g2(x(k-1)(s),s))(t-s)α-1ds|2≤

f(x(k-1)(s),s)|2ds+

g1(x(k-1)(s),s)|2ds+
g2(x(k-1)(s),s)|2ds≤


(8)
由式(7)得
E|x(2)(t)-x(1)(t)|2≤

由归纳法, 得
E|x(k+1)(t)-x(k)(t)|2≤
由式(8)的证明, 不难看出
从而
即{x(k)(t)} 在[t0,T]上是均方收敛序列.另一方面
由Borel-Cantelli引理和切比雪夫不等式得, 存在x(t), 使得
从而有
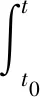


存在性得证.
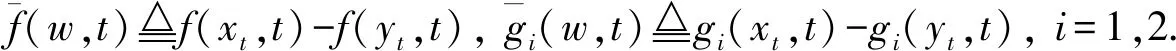
由施瓦兹不等式, 得
令u(t)=E|xt-yt|2, 则由上面不等式得函数u满足
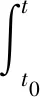
其中,
u(0)=E|x0-y0|2,
由Gronwall不等式, 得
u(t)≤u0eht.
若x0=y0, 则u0=0 且对于所有t≥t0, 有u(t)=0. 从而P{|xt-yt|=0,t∈Q∩[t0,T]}=1.
由xt,yt的连续性得
P{|xt-yt|=0,t∈ [t0,T]}=1.
证毕.
接下来, 考虑当ξ(t)满足一个比(A3)更一般的条件时系统(6)解的存在唯一性.
(A3′): 过程ξ(t) 是Ft-适应且分段连续的, 满足
定理2 若假设(A1)、(A2)和(A3′)成立,则系统(6)在[t0,T] 上有唯一解x(t).
证明存在性. 设x(0)(t)=x0, 对k≥0, 令
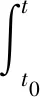


由(A2)知, 存在一个常数d>0, 使得|f(0,t)|+|g1(0,t)|+|g2(0,t)| |x(1)(t)-x0|= |x(k+1)(t)-x(k)(t)|≤ 由于x(t) 在t∈[t0,T] 上是连续的,ξ(t) 是 Ft-适应的, 则 x(0)(t) 和x(1)(t) 是Ft-适应的.由递归过程知x(k)(t) 是Ft-适应的, 因此x(t)也是Ft-适应的. 存在性得证. 这里ε是任意正数.由Gronwall不等式, 得 证毕. 本文考虑了由二阶矩过程驱动的随机分数阶非线性系统, 在Lipschitz条件和线性增长条件下, 证明了二阶矩过程驱动的随机分数阶非线性系统解的存在唯一性问题. 在接下来的研究中, 将考虑由二阶矩过程驱动的随机分数阶非线性系统解的稳定性问题.




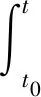

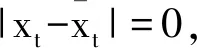
4 结束语
