Zhang Tao Wei Haiguang Mo Xutao

(School of Mathematics and Physics, Anhui University of Technology, Ma’anshan 243000, China)

Abstract：In order to enhance the image contrast and quality, inspired by the interesting observation that an increase in noise intensity tends to narrow the dynamic range of the local standard deviation (LSD) of an image, a tree-structured group sparse optimization model in the wavelet domain is proposed for image denoising. The compressed dynamic range of LSD caused by noise leads to a contrast reduction in the image, as well as the degradation of image quality. To equalize the LSD distribution, sparsity on the LSD matrix is enforced by employing a mixed norm as a regularizer in the image denoising model. This mixed norm introduces a coupling between wavelet coefficients and provides a tree-structured group scheme. The alternating direction method of multipliers (ADMM) and the fast iterative shrinkage-thresholding algorithm (FISTA) are applied to solve the group sparse model based on different cases. Several experiments are conducted to verify the effectiveness of the proposed model. The experimental results indicate that the proposed group sparse model can efficiently equalize the LSD distribution and therefore can improve the image contrast and quality.

Key words：local standard deviation；group sparse; image denoising; mixed norm; texture;

Image restoration is a major subtopic in image science and has been extensively studied over the past decades. The purpose of image restoration is to reconstruct a high-quality image from its degraded observation. It is typically treated as an ill-posed linear inverse problem that can be generally formulated as

b=Hx+n

(1)

wherebis the degraded observation;xis the desired true image; andnis Gaussian white noise with a zero mean. Note thatHis a matrix representing a linear degradation operator.

To address the ill-posed nature of the image restoration problem, image prior knowledge is usually employed to regularize the solution of the following minimization problem:

(2)

where the first term is the data fidelity term and the second termΦ(x) is known as the regularization term, which regularizes the solution by enforcing certain prior constraints. In addition,λ>0 is the regularization parameter, which controls the balance between the fidelity and regularization terms.

How to select a good regularization term is an active area of research. Traditional regularization methods include Tikhonov regularization[1]and total variation (TV) regularization[2]. The total variation measure has been shown to be suitable for preserving sharp edges. Although TV regularization has been proven to be very useful in many applications, it is flawed in that it removes textures and creates staircase artifacts. Texture preserving methods such as sparse representations, non-local methods[3-5]and the deep convolutional neural network (CNN)-based method[6-7]have been introduced as image restoration approaches. Sparse regularization is a recent and successful method to solve image restoration problems[8-9]. Most sparse-based methods represent signals from a given dictionary and then process the coefficients of expansion individually. However, in addition to sparsity, signals may exhibit a “group sparsity” structure. Group sparsity is usually modeled by introducing a coupling between coefficients in the same structure set[10-12]. In the framework of variational formulation, this type of coupling may be introduced by a suitable regularization term[13]. In this study, we introduce a mixed norm regularization term, which enforces the sparsity on the LSD matrix of the restored image.

LSD is an important measure for the structural information of the image[14-15]. Through numerical experiments, we observed that the dynamic range of LSD decreases with an increase in noise intensity. Enforcing the sparsity of LSD matrix can efficiently equalize the LSD distribution. In this study, we examine the wavelet characterization of the LSD matrix of an image, and then propose a group sparse optimization model in the wavelet domain.

We describe the wavelet characterization of the LSD matrix, and then introduce the tree-structured group sparse model in the wavelet domain. Secondly, we give the solution of the proposed model based on different cases through the ADMM and FISTA techniques. Finally, some numerical experiments are presented to verify the potential of the proposed model.

1 Wavelet Characterization of LSD Matrix

In this study, an image is interpreted as a function defined on the unit squareI=[0,1]2. LetQbe the collection of dyadic cubes contained inI.

(3)

wherej=0,1,…;k=(k1,k2)∈Γj={0,1,…,2j-1}2.

Letφandψbe a univariate wavelet constructed out ofVj, which is anr-regular multiresolution approximation ofL2(R2)withr≥1(for the exact conditions, see Ref.[16]). Two dimensional wavelets can be constructed by a tensor product

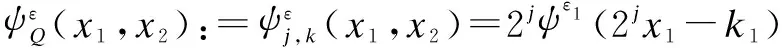
wherej∈Ζ,k=(k1,k2)∈Ζ2,ε∈E=(ε1,ε2)2/{0,0} withεj=0 or 1,ψ0=φ, andψ1=ψ.

One can easily construct periodic wavelets onL2(I) that can be used to decompose periodic functionfonL2(I).

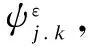
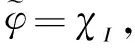
(4)

and theL2norm offcan be characterized by wavelet coefficients:

(5)

In this subsection, we derive the wavelet characterization of the LSD matrix offon dyadic regionQJ,K. The LSD matrix is defined as

(6)

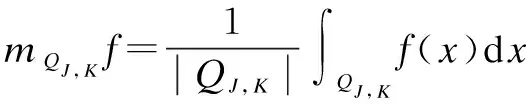
The LSD matrix characterizes the local oscillating property of the image. Different components of an image may have different LSD. In a homogenous region, the LSD is rather small, while in an edge and texture region, the LSD becomes large. Generally, the LSD of noise is much smaller than that of texture. Thus, LSD is often used to separate homogeneous and textured regions in natural image denoising.

In Ref.[17], we derive the discrete wavelet characterization of the LSD matrix, which can be described by the following theorem.

Theorem1The LSD matrix offon dyadic regionQJ,Kcan be characterized by wavelet coefficients as follows:

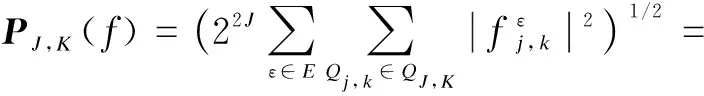
(7)

ProofLetC(QJ,K) denote the mean value off(x) onQJ,K,then

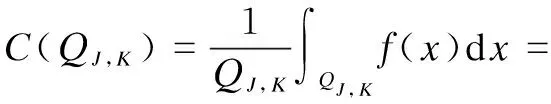
(8)

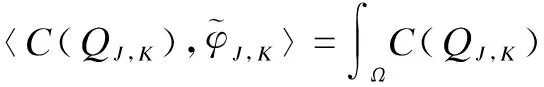
(9)

We writef(x) asf(x)=f1(x)+f2(x)+C(QJ,K), where

(10)

By Eq.(9), we can obtain

(11)

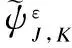
(12)

Then,

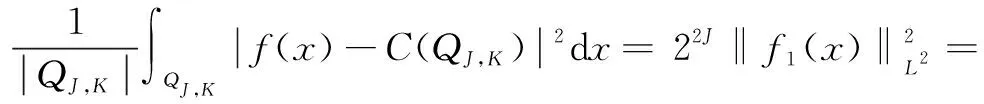
(13)

Then, we can obtain

2 Group Sparse Model in The Wavelet Domain

PJ,K(f)=2J‖αGK‖2K∈ΓJ

(14)

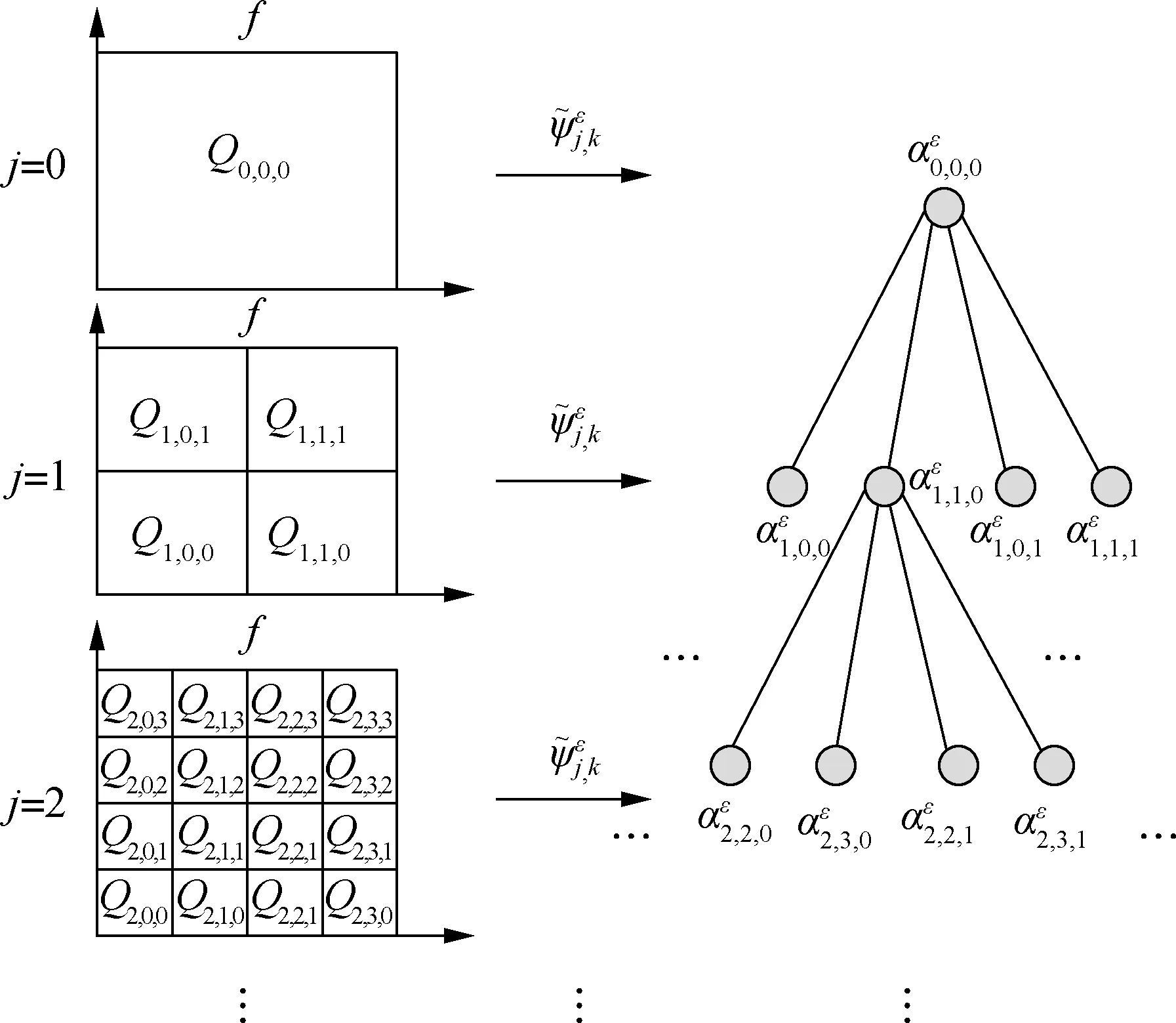
Fig.1 Tree-structured wavelet coefficients

In this study, we introduce the prior that the LSD matrixPJ,Kis sparse. This can be obtained by minimizing thel1norm of the LSD matrix. In other words, we use the following weightedl2,1norm as a regularizer:

(15)

whereωKare weights associated with each group. Properly choosing weights may result in improved recovery performance. In this study, we chooseωKas

(16)

The mixed norm in Eq.(15) explicitly introduces the coupling between wavelet coefficients instead of the usual independence assumption oflpnorm sparse optimization problems. Thus, we consider the following regression problem to recover the group sparse solution:

(17)

wherebHis the high-frequency component of observed imageb, andWis the wavelet transform.ωKcontrols the group sparsity level adaptively. While the image regions are dominated by texture and edges,PJ,Kis relatively large andωKis relatively small. Then, the wavelet coefficients groupαGKis less penalized such that the edges and texture are well preserved during denoising. Conversely, in homogeneous image regions,PJ,Kis relatively small andωKis relatively large. Then,αGKhas more intense shrinkage to enhance the denoising process.

Because most of the noise is concentrated in the high-frequency component, we must only recover the high-frequency component of the image. Ifα*is the solution of model (17), then the final restored image isb*=WTα*+bL, wherebLis the low-frequency component of the observed image.

Our intent is not to seek a state-of-the-art denoising method, but rather to investigate the sparsity of LSD as signal priors and compare it to the TV-based, frame-based and non-local mean methods.

3 Solution of the Proposed Model

We apply the ADMM to solve model (17) whenHis identity andWTis a linear operator (for the ADMM algorithm, see Ref.[18]). To accomplish this, we introduce an auxiliary variable and transform model (17) into an equivalent form:

(18)

s.t.Z=α

(19)

The augmented Lagrangian problem takes the form:

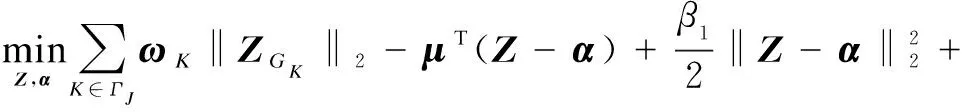
(20)

whereμ>0 is a multiplier andβ1is a penalty parameter. We then apply the ADMM to minimize the Lagrangian problem alternately with respect toZandα.

Theαsubproblem is given by

(21)

Note that(21) is a convex quadratic problem. Therefore, its solution is

(22)

For theZsubproblem, it is reduced to minimize (20) with respect toZ:

(23)

By simple manipulation,(23) is equivalent to the following problem:

(24)

This can be solved by group-wise soft shrinkage:

(25)

The multiplierμis updated by

μ←μ+τ(Z-α)

(26)

whereτis the step length. In summary, we obtain the algorithm for solving model (17) by ADMM as shown in the following:

Algorithm1ADMM for model (17) whenHis identity

Input:bH,Z0,μ0,β1,β2,τ.

Iteration:Fork=1,2,…, until a stopping criterion is reached,

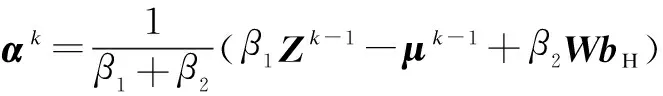
Output:αk.

Note that regularizer ‖·‖lw,2,1is non-smooth but convex, whereas the fidelity term is smooth and convex. Thus, in the following we apply the iterative shrinkage-thresholding algorithm (ISTA) to solve the general case of model (17). The general step of ISTA is described as

αk+1=Proxtkg(αk-tkWHT(HWTαk-bH))

(27)

whereg(·)=λ‖·‖lw,2,1is the mixed norm functional proposed in (15), and Prox is the proximal operator. The proximal algorithm is an efficient tool for non-smooth minimization problems. In proximal algorithms, the base operation is to evaluate the proximal operator of a function, which involves solving a small convex optimization problem. The proximal operator is defined by

Therefore, the Proxtkgoperation in (27) can be expressed as

(28)

The Prox operation can be easily solved by group-wise shrinkage, that is

Proxtkg(x)=GShink(x,λtkω)

(29)

Although ISTA has the advantage of simplicity, it has also been recognized to be a slow method. The fast iterative shrinkage thresholding algorithm (FISTA) is the accelerated version of ISTA[19]. It not only preserves the computational simplicity, but also exhibits a significantly faster convergence rate than standard gradient-based methods. Algorithm 2 summarizes the FISTA for solving model (17), which is described as follows:

Algorithm2FISTA for model (17)

Input:bH,α0=0,t1=1,y1=α0,L,λ.

Iteration: Fork=1,2,…, until a stopping criterion is reached,

Output:αk.

4 Experiments

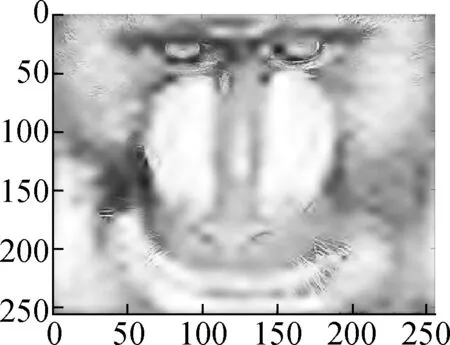
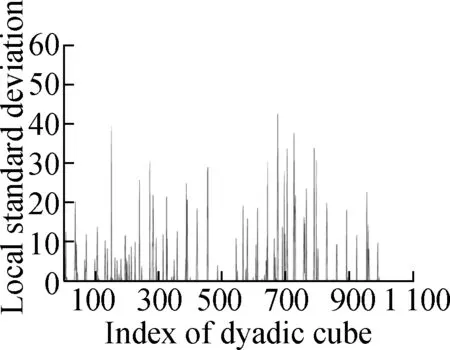
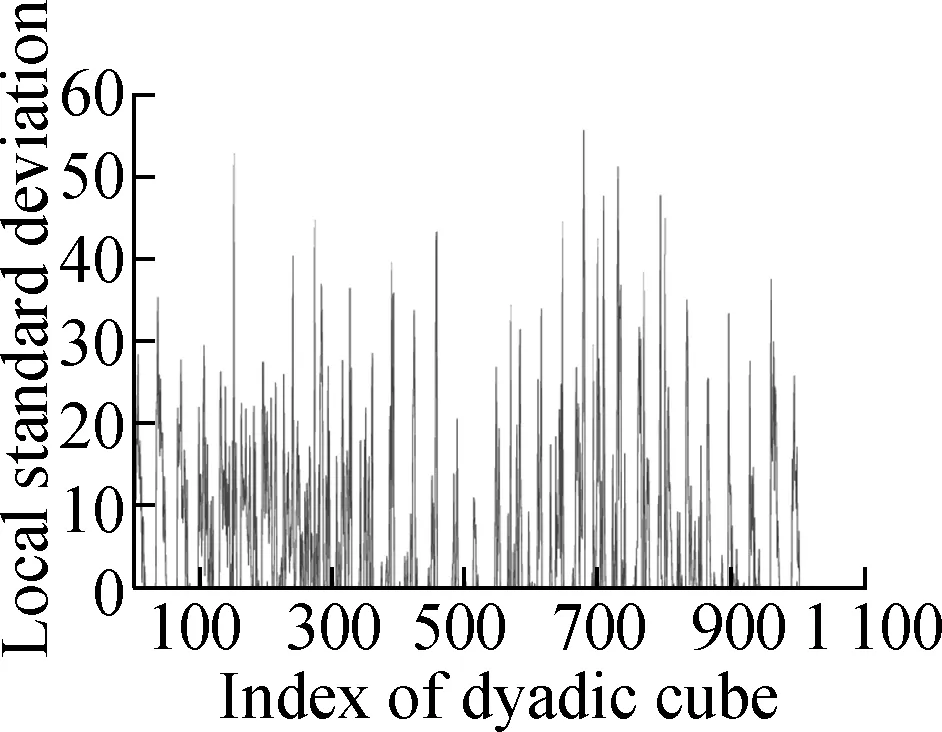
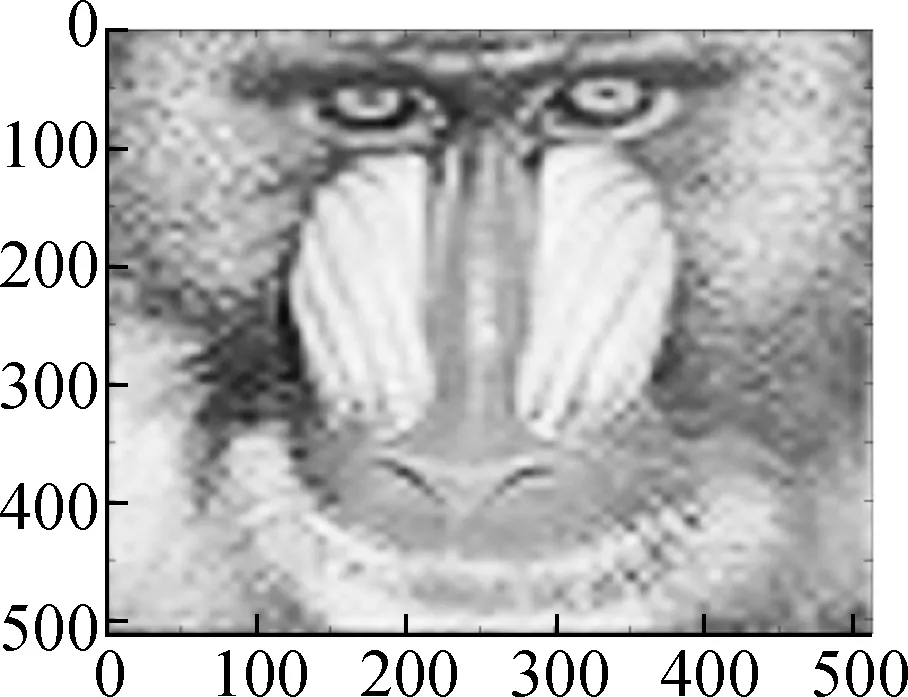
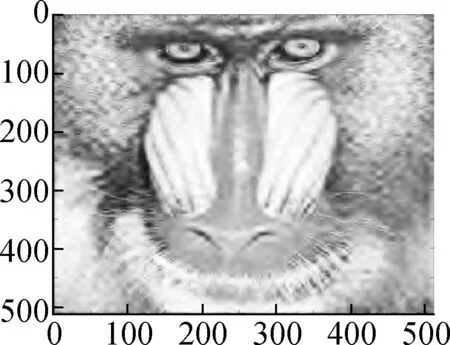
In this section, we present various experiments to show the performance of the proposed method for image denoising. In all the experiments, we chose the periodic “sym4” wavelet and scaleJ=6. First, we describe the group sparse approximation performance of the proposed model based on a noiseless case, as shown in Figs.2 and 3. Fig.2(a) shows the original “Baboon” image and Fig.2(b) shows the plot of the vectorization of its LSD matrix. The vectorization is obtained by stacking the columns of the LSD matrix on top of one another. From the plot of vectorized LSD matrix, we can easily observe its sparsity.

Figs.3 (a) to (d) show the group sparse approximation with parametersβ2=0.001, 0.002, 0.004 and 0.007, respectively. Figs.3(e) to (h) show the corresponding vectorized LSD matrix. There are a total of 1 024 groups of wavelet coefficients, and the percentages of non-zero groups of the approximation image with different parameters are listed in Tab.1.

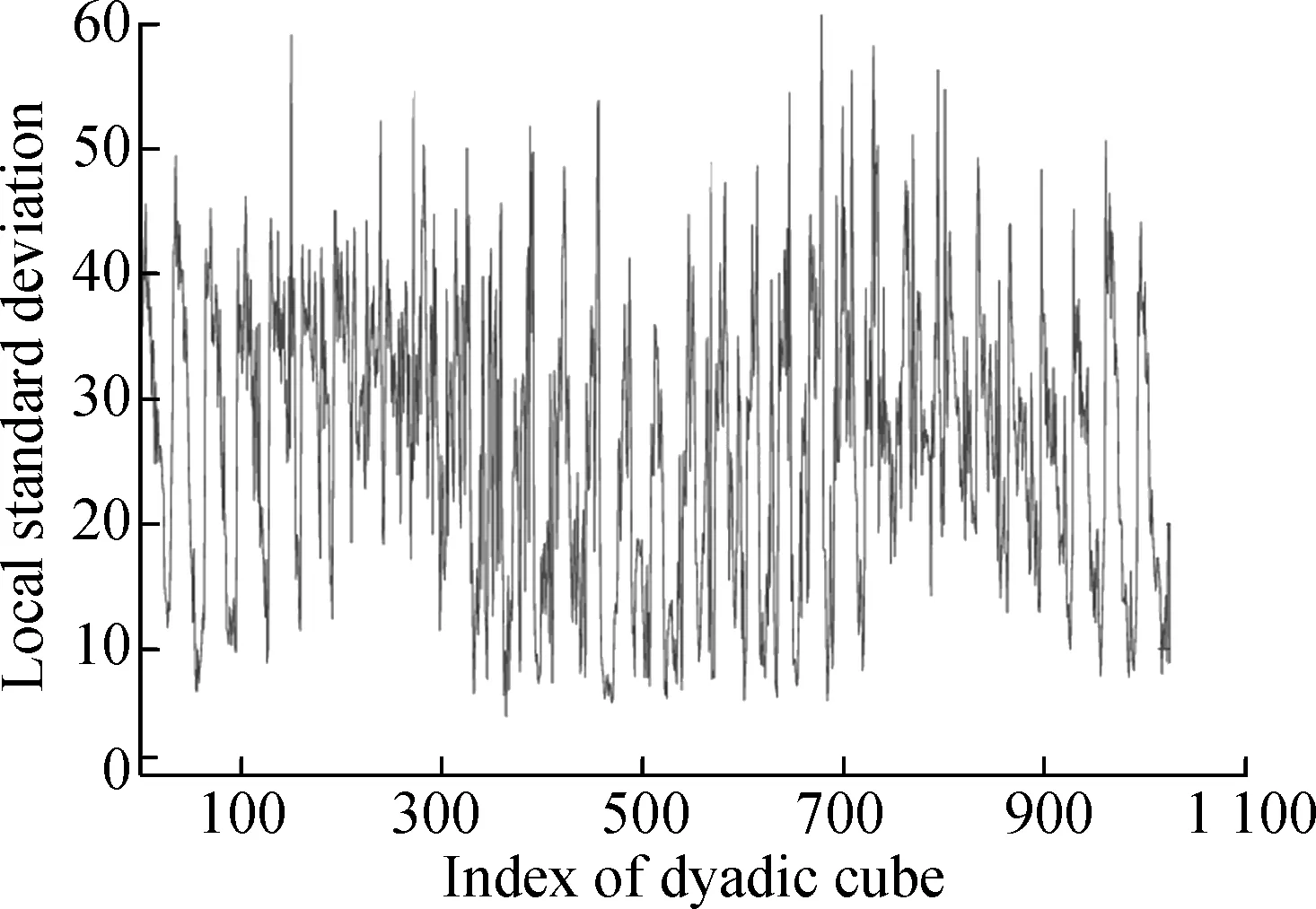
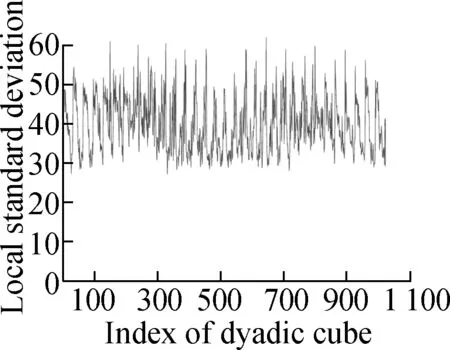
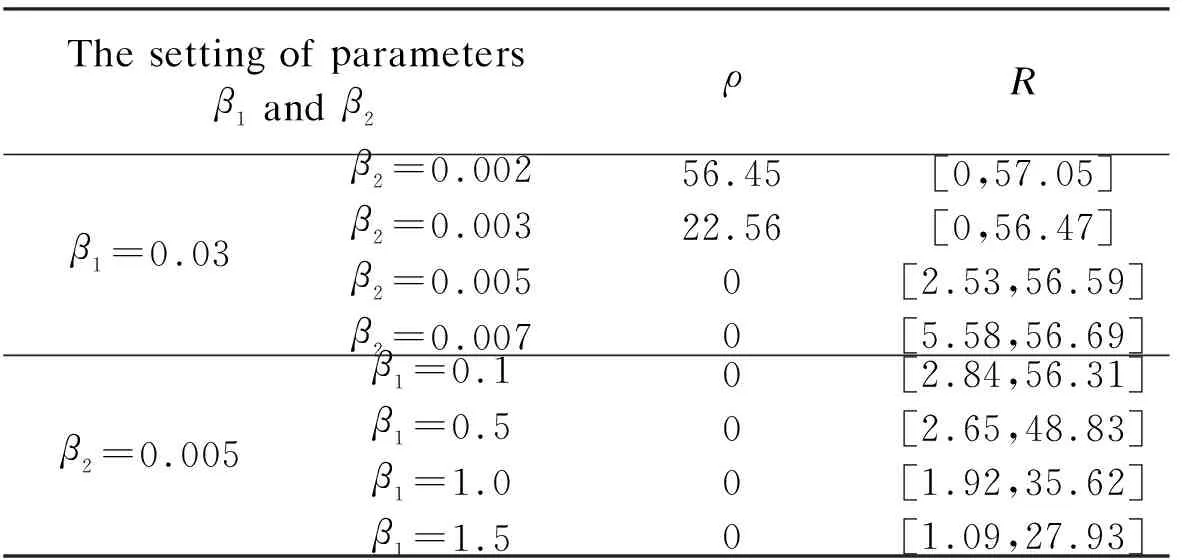
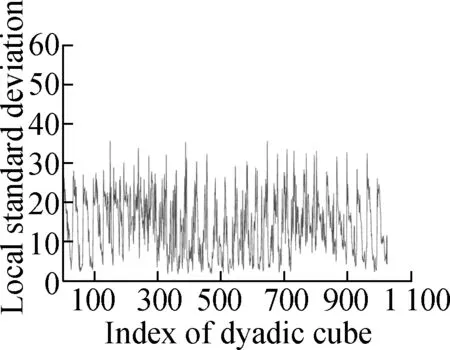
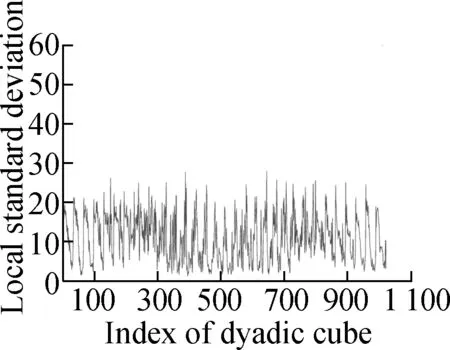
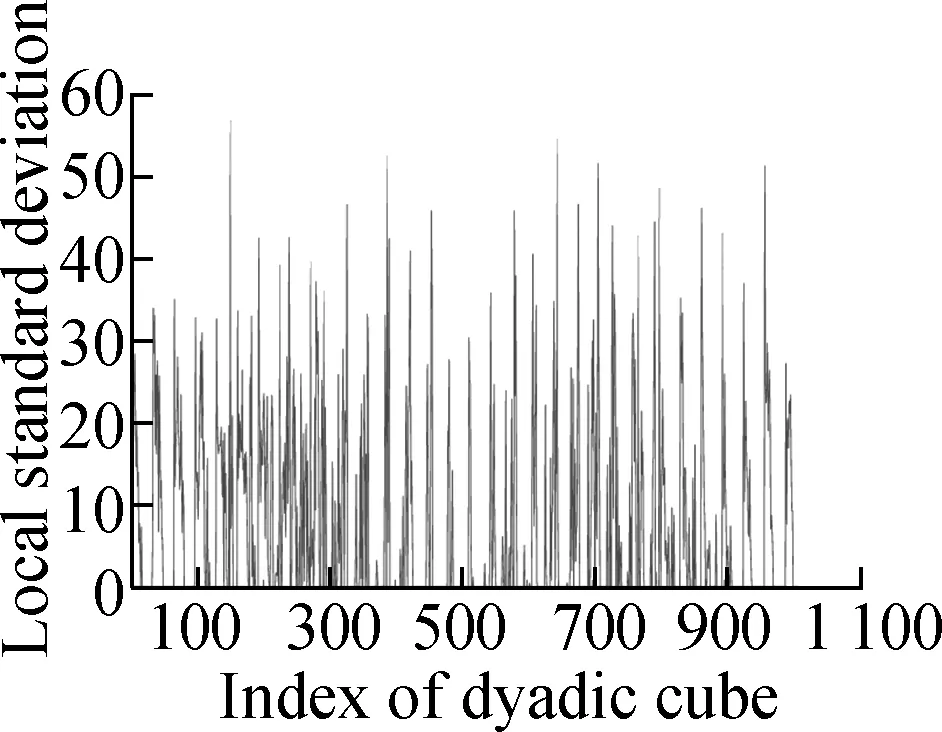
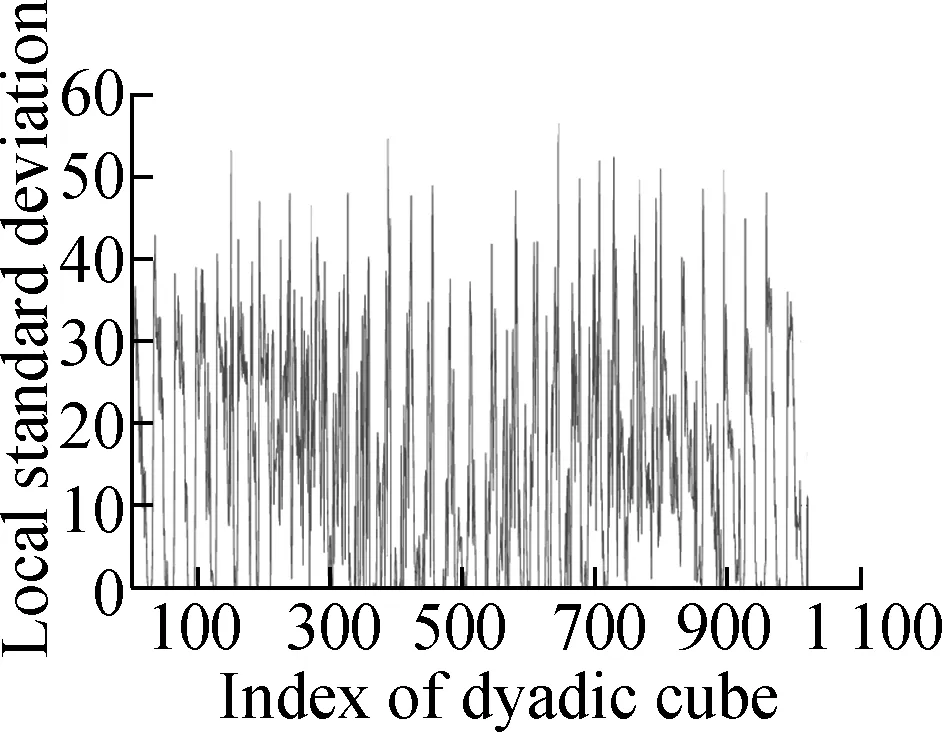
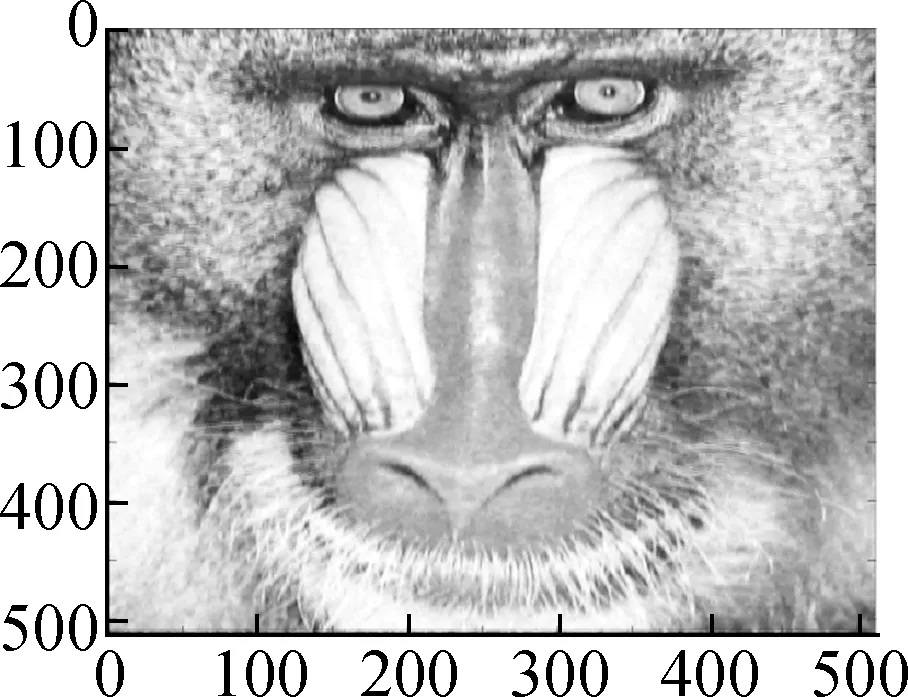
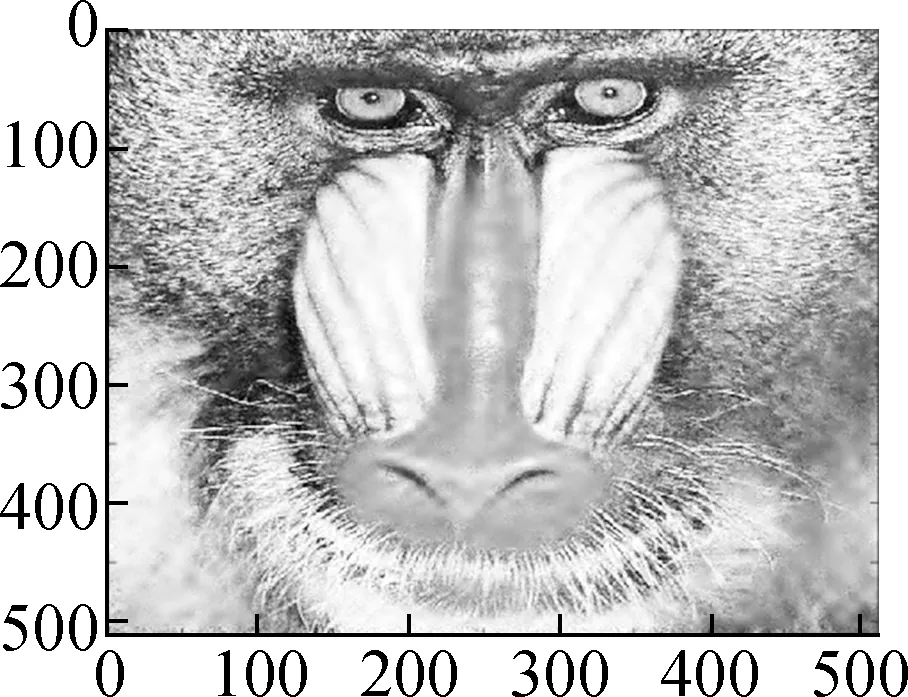
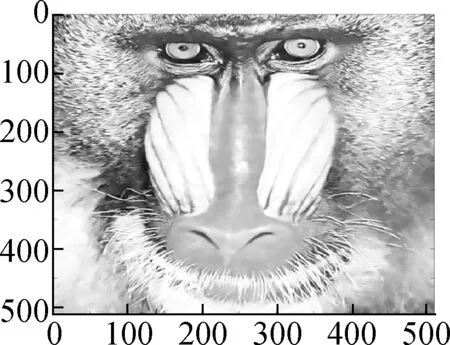
Fig.4 shows the evolution of the LSD matrix along with the noise level. Figs.4(a) to (c) show the noisy Baboon images degraded by three levels of Gaussian noise with a mean of zero and standard deviations of 10, 20, and 30, respectively. Figs.4(d) to (f) show the corresponding vectorized LSD matrix. We can see that the dynamic range of the LSD matrix becomes increasingly narrow with each increase in the standard deviation. The dynamic range of the LSD matrix is defined as We apply the ADMM algorithm to equalize the LSD matrix of the noisy Baboon image (σ=15). In Fig.5 and Tab.2, we present the experimental results to show how parametersβ1andβ2affect the group sparsity and the range of the LSD matrix. We can see that parameterβ2controls the group sparsity of the solution and parameterβ1controls the range of the LSD matrix. The group sparsity can be measured by the group sparsity rateρ, which is the percentage of the non-zero groups.

(a)

(b)

(a) (b) (c) (d)

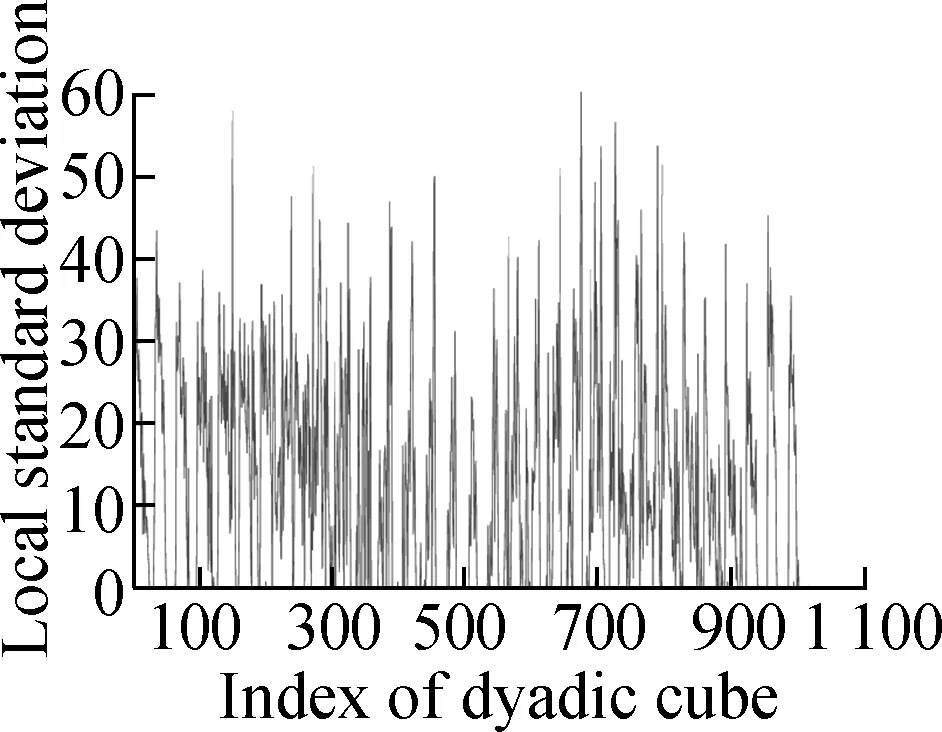
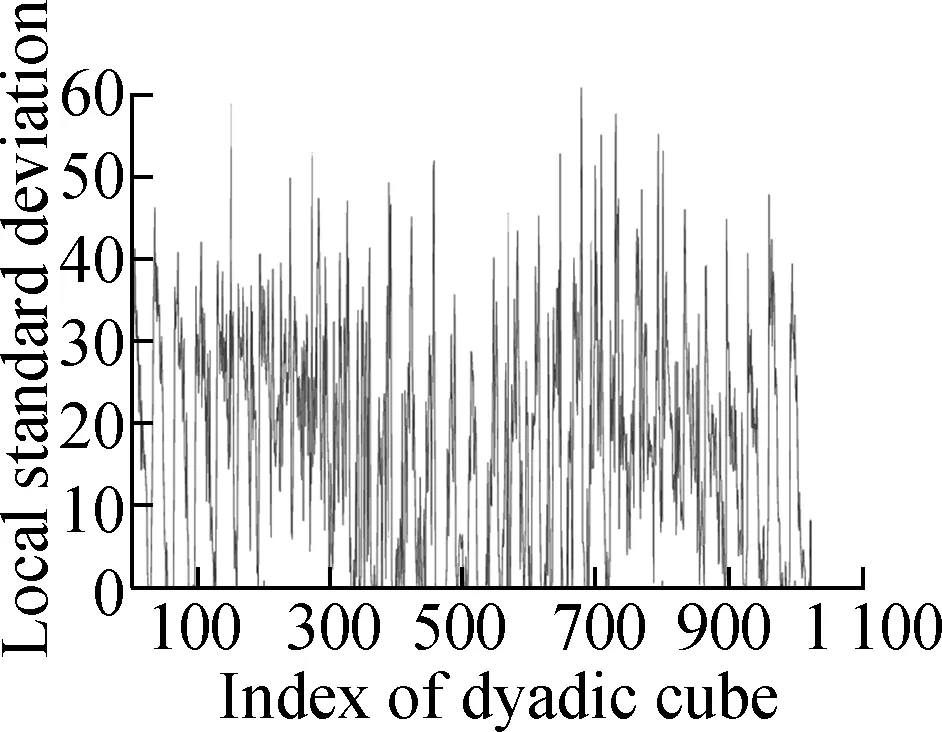
(e) (f) (g) (h)

Tab.1Group sparse approximation performance with different parameters

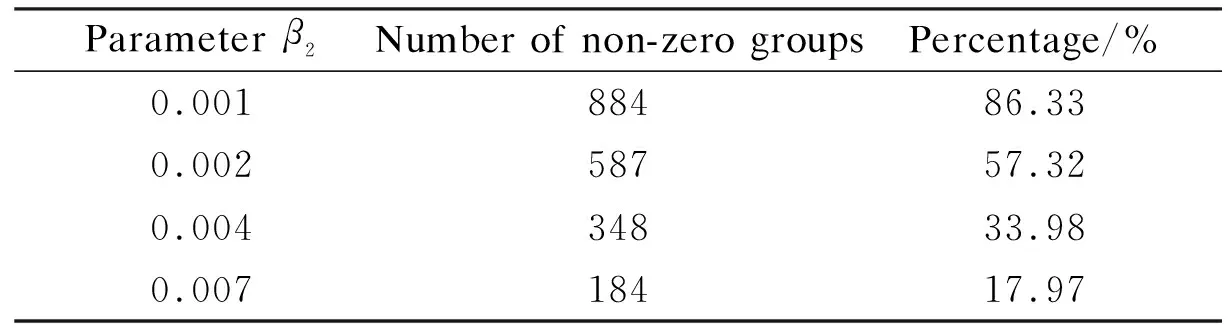
Parameter β2Number of non-zero groupsPercentage/%0.00188486.330.00258757.320.00434833.980.00718417.97

(a) (b) (c)

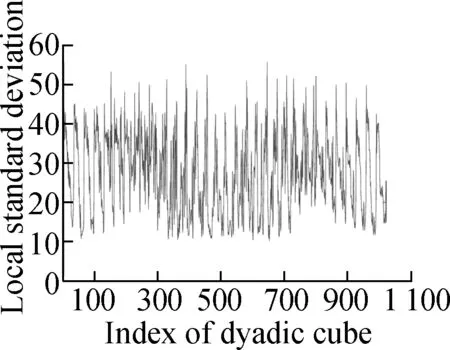
(d) (e) (f)

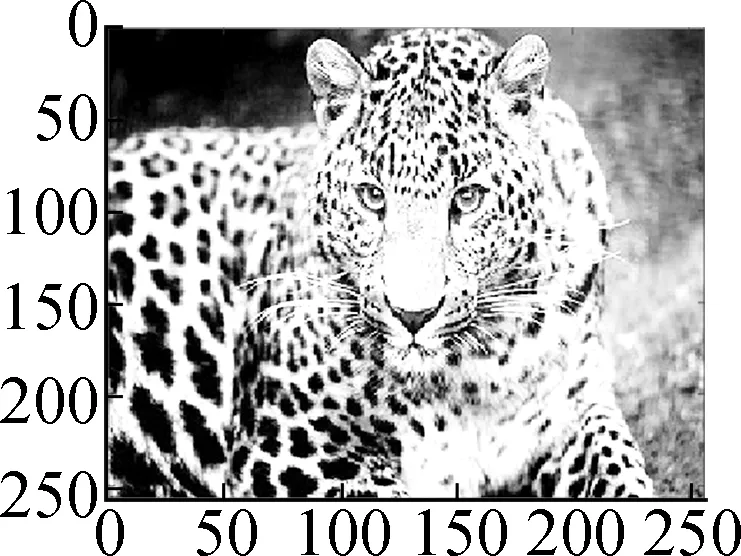
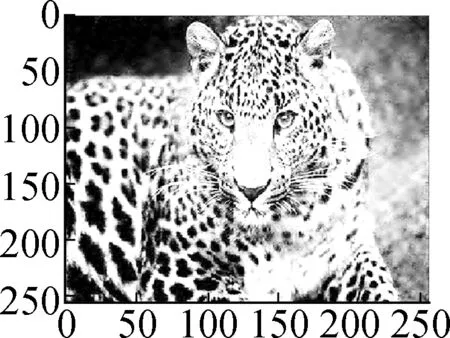
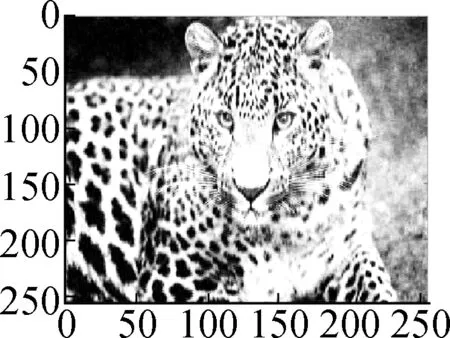
In Figs.6 to 8 and Tab.3, the denoising performance of Algorithm 1 is compared with that of the wavelet shrinkage model, TV model, balanced frame-based model[8], and non-local mean model[5]. We can see that the proposed model outperforms the wavelet shrinkage model and frame-based model, and achieves a competitive performance as compared with the TV model and non-local mean model.

Tab.2Impact of parametersβ1andβ2onρandR

The setting of parameters β1 and β2ρRβ1=0.03β2=0.002β2=0.003β2=0.005β2=0.00756.4522.5600[0,57.05][0,56.47][2.53,56.59][5.58,56.69]β2=0.005β1=0.1β1=0.5β1=1.0β1=1.50000[2.84,56.31][2.65,48.83][1.92,35.62][1.09,27.93]

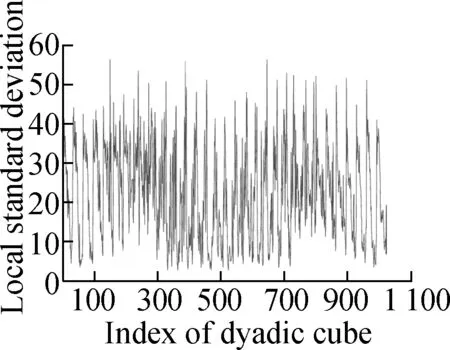
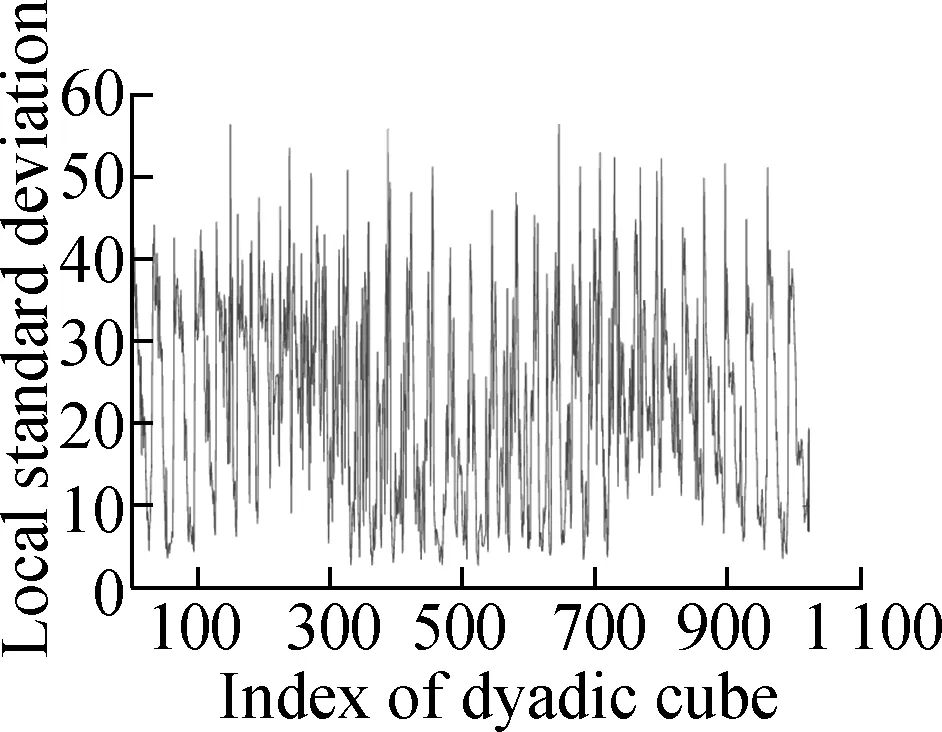
(a) (b) (c) (d)

(e) (f) (g) (h)

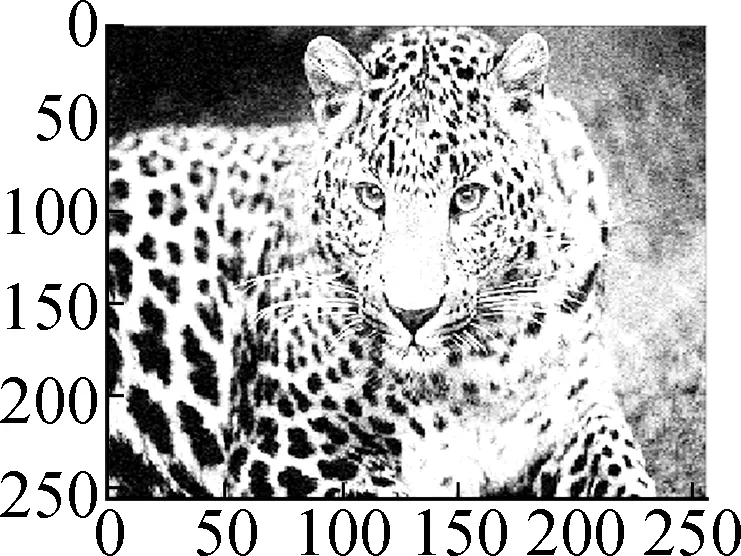
ModelHill(σ=10)House(σ=10)Parrot(σ=15)Leopard(σ=15)Baboon(σ=15)Barbara(σ=20)Man(σ=20)Soft shrinkage 26.6226.4523.6417.9321.1823.1224.98Frame28.0930.4025.8723.7422.0524.3126.74TV29.9331.7328.6125.7826.0326.3229.14Nonlocal mean30.1232.4129.1925.4026.7730.3629.16Proposed model30.7532.3429.0526.3626.8226.8628.90

(a) (b) (c) (d)

(e) (f) (g) (h)

(a)

(b)

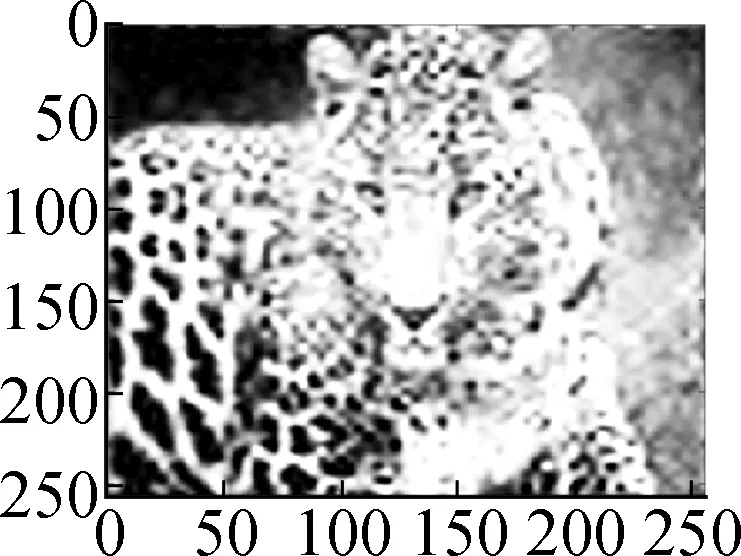
(c)

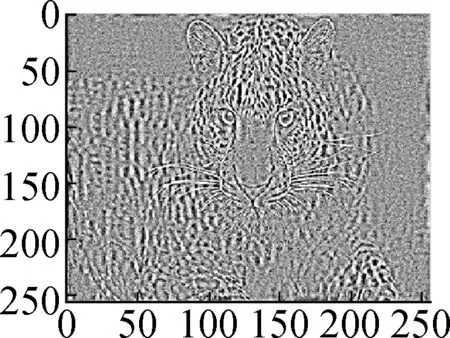
(d)

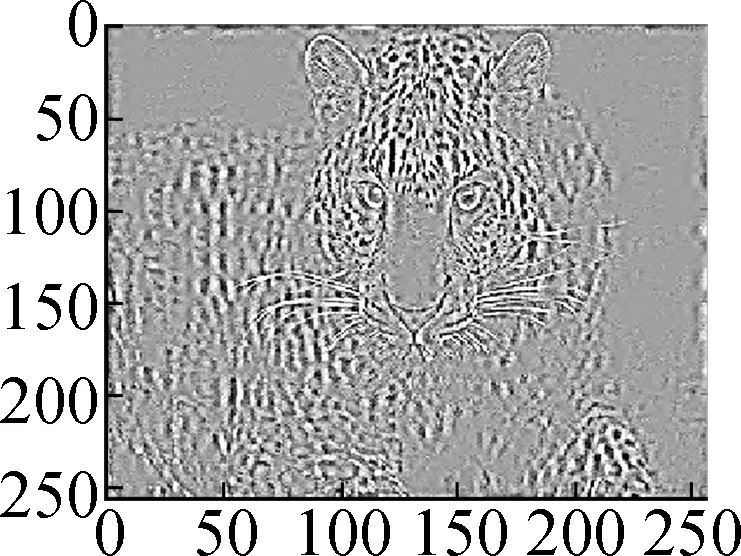
(e)

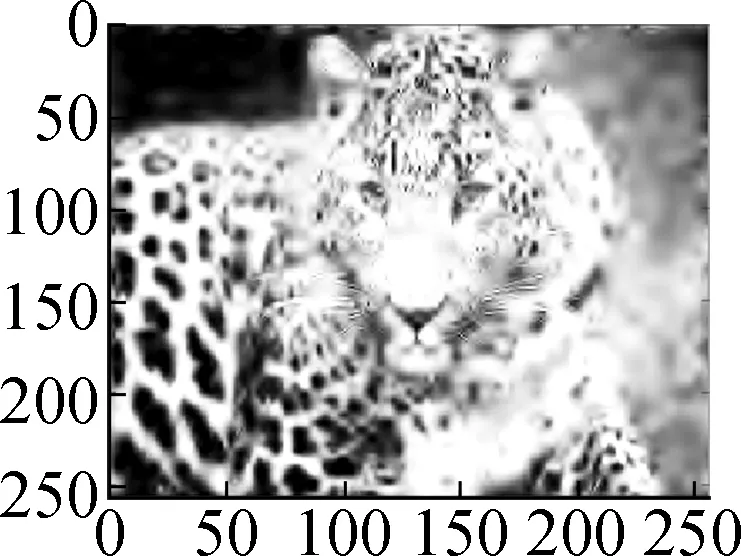
(f)

(g)

(h)

(i)

(j)

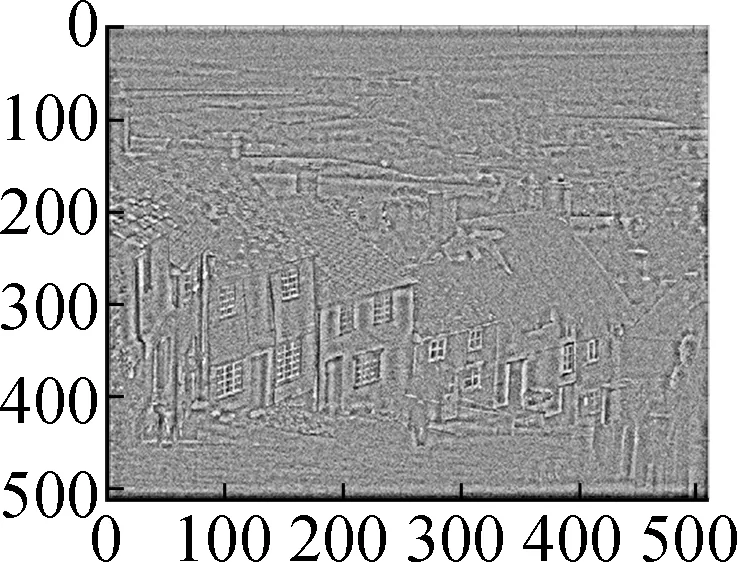
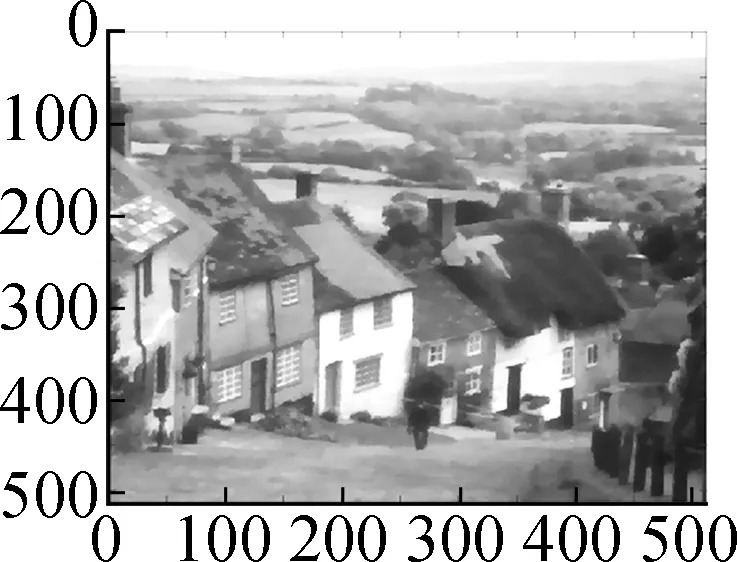
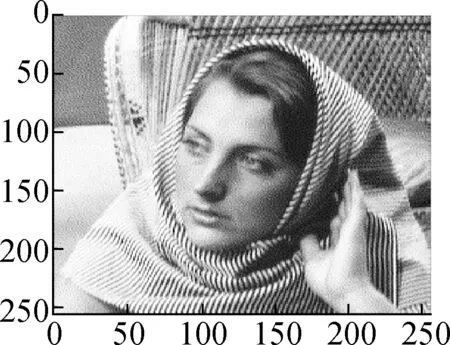
Fig.9 shows the results of Algorithm 2 on the woman image. The test image is contaminated by salt and pepper noise with noise intensityd=10%. After wavelet decomposition, most of the noises are concentrated in the high frequency component, which can be seen in Fig.9(c). Fig.9(d) shows the restored high-frequency component by the proposed model. One can see that most of the noises are removed and the textures are well preserved. Figs.9(e) to (g) compare the restored image by our method with that by the balanced frame-based method and non-local mean method. Particularly in the tagged region, we can see that the proposed method preserves more textures and achieves a better subjective visual effect.

(a)

(b)

(c)

(d)

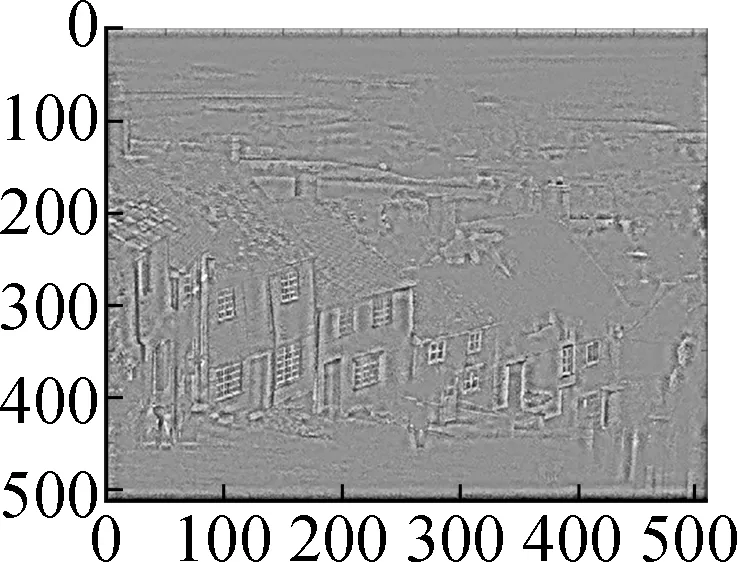
(e)

(f)

(g)

(h)

(i)

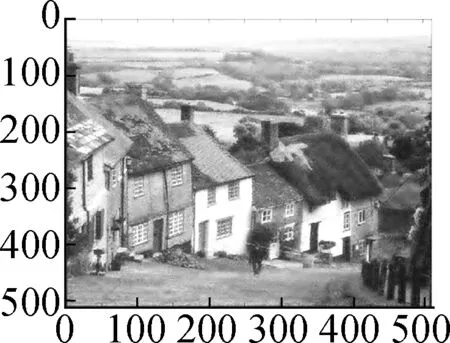
(j)

(a) (b) (c) (d)

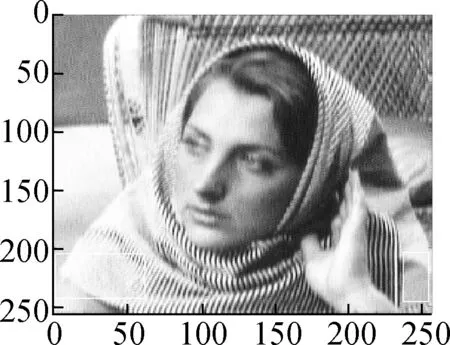
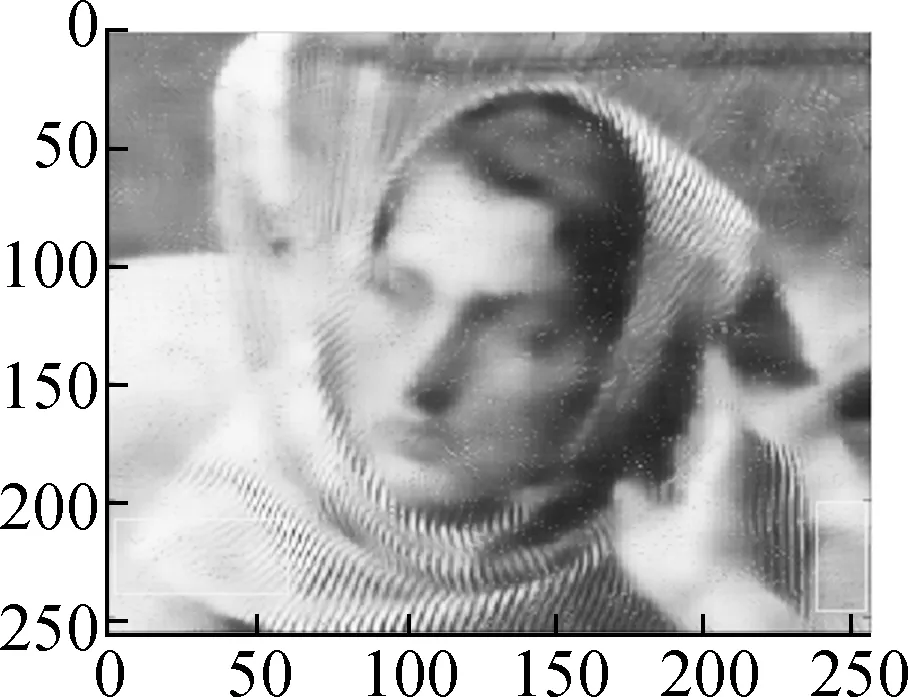
(e) (f) (g)

5 Conclusions

1) Based on the wavelet characterization of the LSD, we find that thel1norm of the LSD matrix is equivalent to al2,1mixed norm of the wavelet coefficients. This mixed norm introduces a coupling between wavelet coefficients and determines a variable group scheme.

2) We find that enforcing the sparsity of the LSD can efficiently equalize the LSD distribution. Thus, we propose a novel group sparse optimization model in the wavelet domain for image denoising. Encoding the group information in addition to sparsity leads to better signal feature selection.

3) The group sparse optimization problem is more difficult to solve than the conventionall1norm regularized problem. We applied the ADMM and FISTA to solve the group sparse model efficiently based on different cases.

4) Several experiments reveal that the proposed group sparse model outperforms traditional wavelet-based model and frame-based model, and has competitive performance with TV and non-local mean image restoration models.