翟登鑫, 阿依古丽·马木提

(1. 喀什大学 数学与统计学院, 新疆 喀什 844000; 2. 新疆大学 数学与系统科学学院, 新疆 乌鲁木齐 830046)

1 引言及预备知识

互连网络的拓扑结构通常由一个连通图G=(V,E)来表示,其中顶点表示处理器,边表示通信链路.传统上衡量网络可靠性和容错性的经典参数是连通度和边连通度.若F⊂V(G),图G中删去F中的所有点后,使得G-F是不连通或者是平凡的,则称F是图G的点割.类似地,若S⊂E(G),图G中删去S中的所有边后,使得G-S是不连通或者是平凡的,则称S是图G的边割.图G的连通度用κ(G)表示,则κ(G)=min{|F|:F是G的点割}.图G的边连通度用λ(G)表示,则λ(G)=min{|S|:S是G的边割}.然而这2个参数存在本质的缺点,理想状态下与图G的一个顶点相邻的所有顶点(或边)不可能同时失效,但这在实际网络应用中几乎是不可能的.由于几乎所有同一处理器的相邻处理器或同一处理器的所有链路都有可能同时失效,为了弥补这个缺点,可以通过对G-F的组件增加一些条件或限制来推广经典连通性的概念,其中F表示有故障的点(或边).

无向图G=(V,E)由点集V和边集E组成,其中V是有限集,E是V中任意2个不同元素的无序对构成的集合.如果uv∈E,那么u和v两点是相邻接的,并且u和v是uv边的端点.令v是G中的点,点v的邻集N(v)是与v相邻接的所有点构成的集合,且|N(v)|被称为点v的度数,记作degG(v)或者简记为deg(v).图G中的一些点子集或边子集,记作F,符号G-F表示从G中删除F的元素所得到的子图.令mc(G)为图G中一个极大连通分支的最大阶.图G的点子集F,令N(F)={u∈V(G)-F:u是与F中的点相邻接的点}.点子集V′⊆V,在子图H(H⊆G)中的V′的邻集,被定义为

Vaidya等[1]提出了一类超立方体类网络,称为HL-图(或BC图),它用以下完美匹配运算“⊕”递归定义:HL0={K1},

i={0,1}, n≥1.

显然,HL1={K2},HL2={C4},HL3={Q3,G(8,4)},其中,C4是四圈,Q3是3维超立方体,且G(8,4)是一个递归循环图[2],见图1.

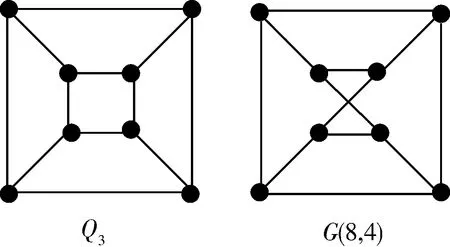
图 1 HL3

HL-图类不仅有小直径,而且有一些优良的特性,如正则性、连通性和哈密尔顿性.文献[3]发现,对HLn中任意满足条件|F|≤2n-3(n≥2)的点集F,HLn-F包含一个连通分支,其阶数至少为|V(HLn)|-|F|-1.同时,对HLn中任意满足条件|F|≤3n-6(n≥5)的点集F,HLn-F包含一个连通分支,其阶数至少为|V(HLn)|-|F|-2.但实际上,HLn中可能有更多故障点.因此,研究HLn中有大量故障点的最大连通分支的最大阶具有重要意义.

引理 1[1,4]设HLn是n维超立方体类网络,则下面4个性质成立:

1) |V(HLn)|=2n;

2) |E(HLn)|=n·2n-1;

3)HLn是n-正则的;

4)κ(HLn)=n.

引理 2[5]设n和k都是正整数,1≤k≤n+1.若F是HLn中点子集,|F|=k,则

此外,F是由HLn中一个点v和它的k-1个邻点组成的点子集,则

引理 3[6]设n、k、x、z都是正整数,1≤k≤n-1,1≤x≤k-1,x+1≤z≤x+(k-1)，若

2k(n+1)-k(k+1)≥-z2+

(2x+2n-1)z+(4-2x2),

则z≤k-1.

定理 1[2]若HLn中任意点子集F,|F|≤2n-3,n≥2,则

mc(HLn-F)≥|V(HLn)|-|F|-1.

此外,HLn中存在|F|=2n-2的点子集F,使得

mc(HLn-F)≤|V(HLn)|-|F|-2.

定理 2[2]若HLn中任意点子集F,|F|≤3n-6,n≥5,则

mc(HLn-F)≥|V(HLn)|-|F|-.

此外,HLn中存在|F|=3n-5的点子集F,使得

mc(HLn-F)≤|V(HLn)|-|F|-3.

2 主要结果

引理 4设n是整数,n≥5,x是实数,则

x2-(2n+5)x+(2n+1+4)>0.

证明令△为一元二次方程:x2-(2n+5)x+(2n+1+4)=0的判别式,则

△=(2n+5)2-4(2n+1+4)=

(4n2+20n+9)-2n+3.

用归纳法可以证明：当n≥5时，2n+3>4n2+20n+9.因此

△=(2n+5)2-4(2n+1+4)=

(4n2+20n+9)-2n+3<0.

因此,一元二次方程无实根,图像全都在x轴上方,结论成立.

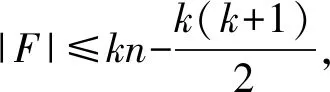
mc(HLn-F)≥|V(HLn)|-|F|-(k-1).

证明令S是HLn中一个点子集,其由一个点v和它的k-1个邻点组成.根据引理2可知

不失一般性,假设F=N(S).显然,

mc(HLn-N(S))=

mc(HLn-F)=|V(HLn)|-|F|-k,

即第二部分成立.

下面用归纳法对第一部分进行讨论.

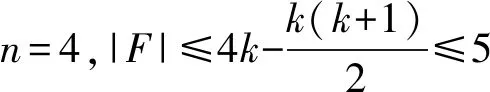
mc(HL4-F)≥|V(HL4)|-5-1.

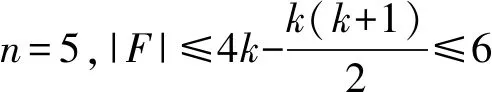
mc(HL5-F)≥|V(HL5)|-6-2.

假设对n成立,其中n≥4.下面证明对n+1也成立.

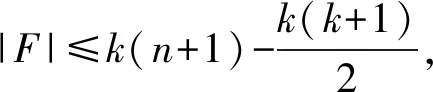
情形 11≤k≤n-2.下面分3种子情形进行讨论.

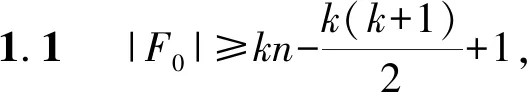
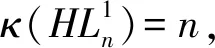
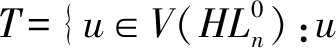
mc(HLn+1-F)≥|V(HLn+1)|-|F|-|T|≥

|V(HLn+1)|-|F|-(k-1).

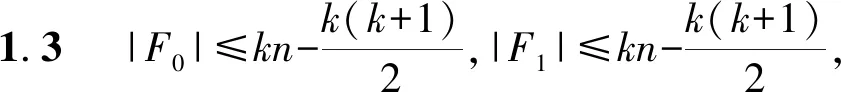
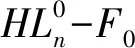
其中0≤p≤r-1,0≤q≤r-1.

根据引理4可知

因此,

|F|+(p+q),

及

|V(C0)|=2n-|F0|-

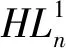
令

进一步,令x=|T0|,y=|T1|,z=x+y,则0≤x≤k-1,0≤y≤k-1,及

mc(HLn+1-F)=|V(C)|=

|V(HLn+1)|-|F|-(x+y).

此时,x=0或y=0.接下来假设x≥1且y≥1.

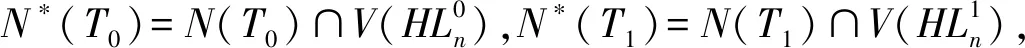
N*(T0)⊆F0,N*(T1)⊆F1.

由此可知

|F0|+|F1|≥|N*(T0)|+|N*(T1)|.

由上述条件及引理2可知

把y=z-x代入上式,化简得

2k(n+1)-k(k+1)≥

-z2+(2x+2n-1)z+(4-2x2),

其中,1≤x≤k-1,x+1≤z≤x+(k-1)≤x+(n-2).

由上式和引理3可知,z≤k-1及

mc(HLn+1-F)≥|V(HLn+1)|-|F|-|T|≥

|V(HLn+1)|-|F|-(k-1).

情形 2k=n-1,则

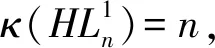
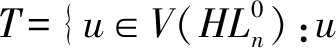
下面分4种子情形进行讨论.

1) |F1|≤n-2,则|T|≤n-2,因此

mc(HLn+1-F)≥|V(HLn+1)|-

|F|-|T|≥|V(HLn+1)|-|F|-(n-2);

2)T∩F0≠∅,则

mc(HLn+1-F)≥|V(HLn+1)|-

|F|-|T|+1≥|V(HLn+1)|-|F|-(n-2);

mc(HLn+1-F)≥|V(HLn+1)|-

|F|-|T|+1≥|V(HLn+1)|-|F|-(n-2);

令N*(T)=N(T)-F1.由假设可知,N*(T)⊆F0.因此

这与引理2的

相矛盾.

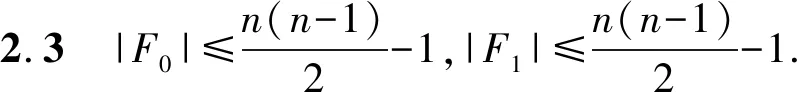
此时,下面的讨论与情形1.3类似.

因此第一部分成立.

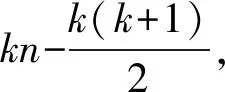
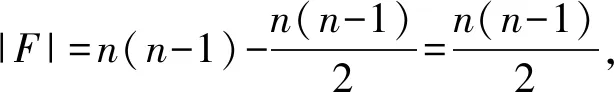
mc(HLn-F)≤|V(HLn)|-|F|-(n-2).

为了能够使得对k=n-1也有类似定理3的结论,可以通过把定理3中F的取值减少1来得到.

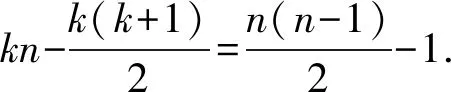
mc(HLn-F)≥|V(HLn)|-|F|-

(k-1)=|V(HLn)|-|F|-(n-3).

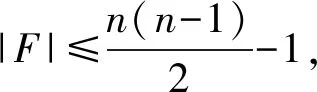
mc(HLn-F)≥|V(HLn)|-|F|-(n-2);