Han-Hai Li(李瀚海), Zhong-Yu Zheng(郑中玉),†, Tian Xie(谢天), and Yu-Ren Wang(王育人),‡

1National Microgravity Laboratory,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China

2School of Engineering Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: hydrodynamic interaction,self-diffusion,ellipsoids,channel

1. Introduction

Confined diffusion is ubiquitous in both natural and industrial processes.[1]In contrast from free diffusion in infinite liquids, the diffusion of particles in a complex medium often leads to the so-called“anomalous diffusion”,which manifests itself as the mean squared displacement(MSD)〈x2(t)〉exhibits a nonlinear relation with time t,[2,3]i.e., 〈x2(t)〉～tαwhere α/= 1. When α ＞1, it corresponds to the super-diffusive motion, which is generally observed in the presence of an external field or the self-motile motion of cells[4-6]or Janus particles.[7]When α ＜1, it corresponds to the sub-diffusive motion, which is suggested to be more ubiquitous in nature and generally occurs in confined diffusion, such as macromolecular crowding in biology,[8,9]polymer solutions,[10-13]hydrogels,[14,15]etc.

Particle diffusion in a narrow channel is a typical confined diffusion that has raised wide concern,[1,16-18]such as porous flow,[16]microfluidic devices,[17]and transfer of species across biological membranes.[18]An isolated particle in a channel has been well studied;[19]however, the multiparticle case,which is more often encountered in practical applications,has not been sufficiently discussed due to the complexity of the interactions between particles,such as collision,coulomb interaction,magnetic interaction,and hydrodynamic interaction.In many multi-particle problems,particles have no charge or magnetism, and collisions between particles do not dominate the motion due to low linear density of particles in the channel. Consequently, the influence on the particles exerted by flow field dominates the motion.[20,21]In a quiescent liquid, Brownian particles receive momentum impulses from thermal fluctuations of the water molecules, and the resulted motion creates a flow field,which affects other particles in its vicinity.[21]Hence,one particle is affected by another one indirectly through the flow field that transfers momentum,known as hydrodynamic interactions(HI),and can dramatically affect the particles diffusive behavior.[20,22]Hydrodynamic interactions are screened[23]under the quasi-one-dimensional(q1D)confinement. Consequently, particles affect each other only when their mutual distances are small and two-body interactions remain dominant.

The hydrodynamic interactions between two particles are influenced by the particles’ shapes.[21]Although more attention is being paid to anisotropic particles (e.g., colloidal ellipsoids,[24,25]bacteria,[26]carbon nanotubes,[27]rigid fibers,[28]and molecules[29]in various geometric systems),most studies focus on the novel self- and collective dynamics rather than hydrodynamic interactions,not to mention how shape affects hydrodynamic interactions. Since most particles in nature and industrial processes are non-spherical,such as the transmembrane transport of ions and proteins,[18]the microfluids for cell culture,[30]bioassay,[31]drug delivery,[32]and lab-on-a-chip,[17]the relationships between HIs and particle shapes are needed in practice.

In this paper,we study the self-diffusion behavior of ellipsoid in two-ellipsoid pair with different aspect ratios p in a narrow channel. By comparing experimental data and numerical simulation results,we prove that the self-diffusion of adjacent ellipsoidal particles is affected by hydrodynamic interactions.The self-diffusion coefficients are relevant to the interparticle separation X and increase in the intermediate time regime.

2. Experimental details

The experiments were conducted using microfluidic labon-a-chip devices. The polydimethysiloxane (PDMS) channels were molded from a photoresist master pattern on a silicon wafer by soft lithography,with 6µm width(w)and 3µm depth(h).

Polystyrene (PS) ellipsoids (＜5% polydispersity) were fabricated by stretching 3.26µm diameter polystyrene spheres(Spherotech Inc.) by the method described in Refs. [25] and[33]. To study the effect of particle shapes (p) on how the HIs affect the self-diffusion behavior, we prepared five ellipsoids with different aspect ratios p=a/b=1.8,2.2,2.8,5.2,and 7.5, where a and b are the semi-major and semi-minor axes of an ellipsoid, and they were measured by the optical microscopy.

A total of 7 mM sodium dodecyl sulfate was added in the suspension to eliminate the surface charge induced direct interaction of neighboring ellipsoids,with a Debye length(＜30 nm)[33]much shorter than the nearest tip-tip distance(～0.4µm)in our measurements. The linear packing fraction ρ =2aN/l was low (0.05-0.3) to identify isolated neighborparticle pairs and eliminate the influence of collision between ellipsoids, where l is the length of the observed channel section and N is the particle number in it. The particle movements were observed by fluorescent microscopy and recorded by charge-coupled device (CCD) with 10 frames per second(fps). The center-of-matter positions and orientations of individual ellipsoids were tracked using image-processing algorithm with 1°angular resolution and 0.12 (0.04) µm spatial resolution along the long-(short-)axis.[24,25]

3. Results and discussion

We study the short-time self-diffusive motion of ellipsoids by measuring their self-diffusion coefficients DSdepending on the axial interparticle separation X, which is defined as DS(X)=〈Δx2〉/2Δt, where Δx is the center-of-mass displacement along the channel axis of the ellipsoid during time interval Δt, the brackets ＜＞denote the data averaged over all ellipsoids without the disturbance of others in a range of[x1-5a, x2+5a], where x1and x2are the axial positions of the left and the right ellipsoid, respectively. We choose the spatial resolution δX =0.4b and Δt=0.1 s to ensure the transient interparticle distance within[X-δX/2,X+δX/2].figure X0/2a in Fig.1(b)and Fig.2,where X0/2a decreases as p increases.

Fig. 1. (a) The self-diffusion coefficients DS of colloidal particles as a function of interparticle distance X, (b) rescaled diffusivities(DS-D′S0)/(DS0-D′S0) as a function of X/2a. Symbol colors and shapes correspond to various p values. The horizontal lines mark DS0 and vertical lines mark X.

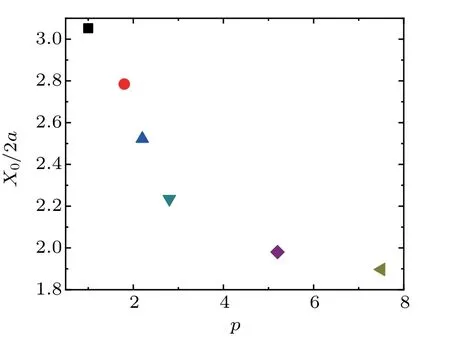
Fig.2. X0/2a as a function of p. Symbol colors and shapes correspond to various p values.

These phenomena indicate that the hydrodynamic interactions between two adjacent colloidal ellipsoids significantly affect the self-diffusion coefficient of each ellipsoid, and the hydrodynamic interactions decay to zero as X increases, and both colloid ellipsoids become isolated ellipsoids when X is large enough. With the increase of p, the effect range of hydrodynamic interactions increases,but the scaled range X0/2a decreases. The reason is that all of the ellipsoids used in our experiment are fabricated by the same kind of fluorescent PS sphere and,therefore,semi-minor axes b decrease with the increase of p, which significantly influences the effect range of hydrodynamic interactions.

To further prove that the variation of DSwith X is caused by the hydrodynamic interactions, we have performed finite element simulations using Comsol Multiphysics v5.3a. In the simulation, we excluded other interactions between particles and solved the Stokes equations for two ellipsoidal particles diffusing in a channel to directly measure the induced flow field between them. The creep flow model in Comsol Multiphysics was used and the particle was a rigid body. To compare experiments and simulations, the geometric parameters in the simulation were chosen to match the ellipsoids with the channel shape that was used in our experiments. No-slip boundary conditions were set on ellipsoids and the walls of channel,open boundary conditions were set on the upper side of channel, and periodic boundary conditions were set at the ends. As mentioned in Ref. [19], the ellipsoids in our experimental system are strongly confined in the channel, which leads to a small angle (≤8°) between their long axis and Xaxis, indicating that the ellipsoid is almost parallel to the Xaxis. Consequently, the long-axis of ellipsoids in our simulation is fixed along the channel.

A transient axial velocity υ1was applied on the left ellipsoid at each X.Figure 3 illustrates the flow fields computed by Comsol for p=1.8 and 7.5. We should notice that the flow in the channel curls around the particle and does not extend far into the channel.When the distance between the two ellipsoids is large enough,the hydrodynamic interaction is screened.[23]In this case, both ellipsoids can be treated as isolated ellipsoids moving in the channel. When the distance between the two ellipsoids is small,the rightward motion of the left ellipsoid induces a rightward flow which pushes the right ellipsoid,leading to a larger hydrodynamic drag force on the left ellipsoid than isolated ellipsoids. It can be understood that two ellipsoids have correlated-diffusion behavior,and such behavior is similar to the self-diffusion of a larger ellipsoid. According to Ref.[19],a larger ellipsoid has a lower diffusion coefficient in this case, which explains why DS＜DS0when X is small.Finally, we find that a more anisotropic ellipsoid induces a stronger flow in a longer range, which explains the larger X and stronger HIs for larger p in Fig.1.

Fig.3. Simulation results of the flow fields created by the translational motion of the left ellipsoid. Black arrows describe the local flow direction. The color represents the local flow speed u in the x direction.p=1.8 in panels(a),(c),and(e),and p=7.5 in panels(b),(d),and(f).X/2a=1.05 in panels(c)and(d),and 3.4 in panels(e)and(f).

The resulting hydrodynamic drag forces F=imposing on the particle pair are proportional to their translational velocities υ=via F = ζ·υ, where ζ is the velocity independent measure of F, known as the friction matrix,[34]which is a 2×2 symmetric matrix in our condition. The diagonal terms (ζ11; ζ22) describe hydrodynamic drag experienced by the moving particles (first; second), and the off-diagonal elements(ζ12=ζ21)denote the force exerted by unit velocity of one particle on the other. The resulting hydrodynamic drag force F on both ellipsoids can be easily obtained from Comsol Multiphysics;i.e.,the friction matrix ζ can be computed. In addition, the matrix of diffusion tensors D is related to the friction matrix by a generalized Einstein relation D(X)=kBTζ-1.[35]This allows us to calculate the simulation diffusion DS(X)at each X and compare the results with the experiment data shown in Fig. 1. Figure 4 show the quantitative comparison between the diffusion coefficient DSobtained by numerical simulation and that obtained in the experiment,where the solid lines indicate the simulation results and the points indicate the experimental values.

The numerical simulation solutions (solid lines) are shown in Fig.4(a),which are in good agreement with the experimental values (symbols). DSdecays exponentially as X decreases when X ＜X0. This effectively proves that in our experimental system, it is indeed the hydrodynamic interactions that influence the self-diffusion behavior between adjacent ellipsoids. Meanwhile,according to the results of numerical simulation, we calculate the D′Sin the extreme case of X =2a, and compare it with the D′S0of an isolated ellipsoid with A=2a and B=b which is used in Fig.1(see Fig.4(b)).From Fig. 4(b), we notice that DS(X =2a)＞DS(A=2a),which indicates that even in the extreme case, the pair composed of two ellipsoids cannot be regarded as a combination of a rigid ellipsoid, and the diffusivity of the ellipsoid pair is greater than that of the rigid ellipsoid.

Fig. 4. (a) The quantitative comparison between the numerical simulation (solid lines) and experimental data (points); symbol colors and shapes correspond to various p values. (b) DS(X =2a) from simulation results (filled symbol) and DS(A=2a) for theory calculate (open symbol).

Earlier,we studied how the hydrodynamic interactions affect the self-diffusion behavior of ellipsoids in a short-time(Δt =0.1 s); however, whether this short-time effect leads to long-time diffusivity changes is unclear. To further study this problem, the self-diffusion behaviors of ellipsoid pairs were characterized by the corresponding mean-squared displacement of individual particles,〈Δx2(t)〉～tα,as shown in Fig.5.The slope of MSD decreases as p increases,while the MSD of different p exhibits qualitatively similar trends.

The diffusion of ellipsoids is characterized by three time regimes,which can be clearly distinguished from Fig.5(b). In the short- and long-time regimes, the unit slope lines (blackdashed lines) indicate linear enhancements and the motions are diffusive with α =1. In the intermediate time regime,the slopes are larger than 1,i.e.,α ＞1,and the motions turn into a crossover region in which the diffusion coefficient increases with the increase of time. The qualitative change of MSD reflects the underlying transition of ellipsoids from particle pair to two isolated ellipsoids.At the beginning of our observation,in a short period of time, X ＜X0, the ellipsoid is affected by the hydrodynamic interaction with the other one,resulting in a linear regime of MSD with a smaller diffusion coefficient than isolated ellipsoids. In the intermediate time regime,the dominant move trend of ellipsoids is separation, and the hydrodynamic interactions promote this behavior, resulting in the crossover region. Finally, in the long-time regimes, the ellipsoid pairs are separated into the isolated ellipsoid and become the self-diffusion behavior of the isolated ellipsoid.

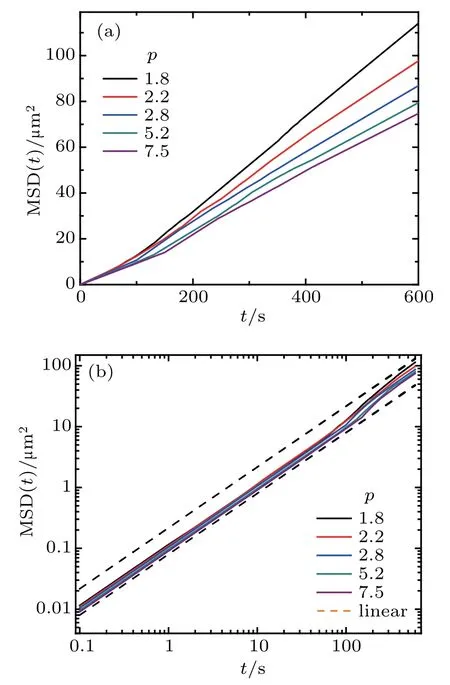
Fig.5. (a) MSDs along the x-direction. (b)Log-log plot of panel (a).Line colors correspond to various p values.

To further elucidate the relationship between the spatial variation of ellipsoid pairs and the diffusion behavior of ellipsoid particles, the statistical data obtained in the experiment are processed as follows: the number of all the ellipsoid pairs with 2a ＜X ＜X0is denoted as nall(t),and we divide[2a,X0]equally into three intervals, A1: X ∈[2a,2a+(X0-2a)/3],A2: X ∈[2a+(X0-2a)/3,X0-(X0-2a)/3], and A3: X ∈[X0-(X0-2a)/3,X0];the number of ellipsoid pairs in interval Ai is nAi(t),and the initial number of particles in each interval at the initial time is determined as N,i.e.,nAi(0)=NAi,where i=1,2,and 3. As time goes on,the ellipsoid pairs may jump out from their initial interval, and we determine the number of the ellipsoid pairs that jump out after time t as nAi-Aj(t),where Ai and A j correspond to the initial interval that ellipsoids jump out and the final interval that ellipsoids jump into,respectively. The values of n(t)/N for various cases as a function of t are shown in Figs.6(a)-6(d)at different p values,and the number of all ellipsoids nall(t)/Nallis plotted in Fig.6(f).

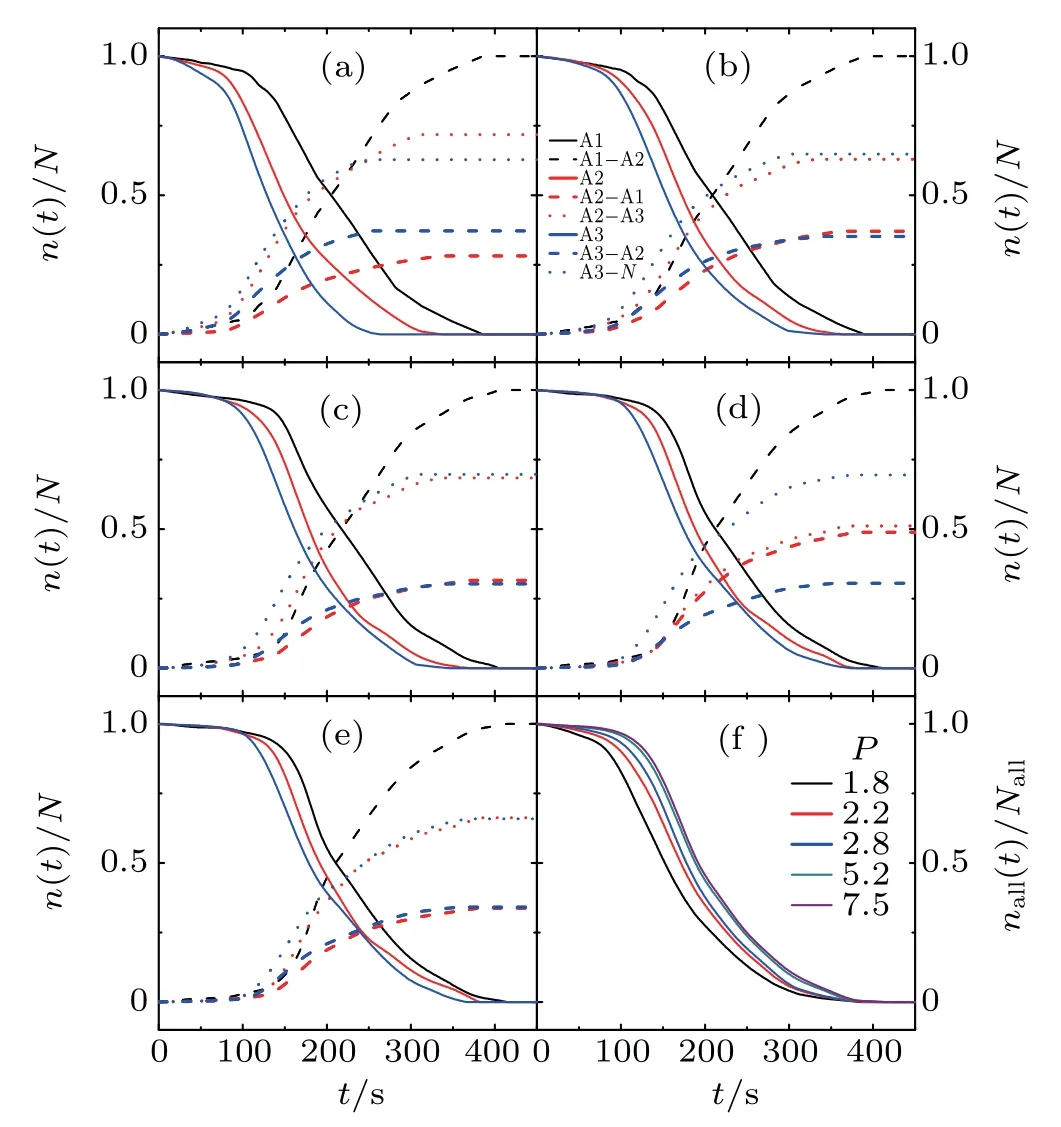
Fig.6. (a)-(e)The value of n(t)/N for various cases as a function of t:p=(a)1.8,(b)2.2,(c)2,8,(d)5,2,and(e)7.5. Line colors correspond to different initial intervals, the dashed lines correspond to the movement that ellipsoids move away from each other, and the dotted lines correspond to the close one. (f) nall(t)/Nall for all values of p. Line colors correspond to different p values.

As shown in Fig.6, the average times for both the ellipsoids jumping to other intervals and the ellipsoids leaving the X range increase with the increase of p.This phenomenon can be explained by the weaker diffusivity of the ellipsoids as p increases, and the smaller self-diffusion coefficient leads to a slower change of the center-to-center separation.For all values of p,the probability of moving to the outside interval is greater than that to the inside,which indicates that in our experimental system with a low enough linear density of particles in the channel,paired particles will become isolated particles after a long enough time.

We define the start time t1and end time t2of the intermediate regime as the point where the local slope deviates by 10%from the unit slope in Fig.5(b),and define t1and t2as the time when the fastest change rate occurs on the n/N curve in Fig. 6(f); namely, the extreme point of the second derivative,and the maximum value corresponds to t1and the minimum to t2. The t1and t2measured from MSD and nall(t)/Nallare shown in Fig. 7 as a function of p. The excellent agreement between them, with the largest discrepancy below 10%, suggests that the spatial variation of ellipsoid pairs induced by the hydrodynamic interactions affects the long-time self-diffusion behavior. Both t1and t2increase with the increase of p, indicating the intermediate time regime starts and ends later at larger p, as mentioned earlier. This is caused by a larger p,which leads to smaller diffusivity so that ellipsoids take more time to diffuse out of the range that HI affects the diffusion.

Fig. 7. The t1 (filled symbols) and t2 (open symbols) measured from MSD(black squares)and n/N (red circles)for different p values.

4. Conclusion

In conclusion, we have utilized microscopic observation experiment to measure the movement of individual ellipsoid diffusing in a narrow channel when two ellipsoidal particles are close to each other. The short-time self-diffusion and MSD are measured to investigate how the HI affects the selfdiffusion behavior of Brownian ellipsoidal particles diffusing under the constraint of q1D channel. Our measurements prove that the self-diffusion coefficients of the ellipsoids are related to the distance X between the two ellipsoids. This relationship is caused by hydrodynamic interactions and proved by quantitative comparisons between the experiment and the numerical simulation. The mean squared displacement of these ellipsoidal particles is measured. In the intermediate time regime,a crossover region in which the diffusion coefficient increases as the time increases is observed. By quantitative comparison of the start time t1and end time t2of the intermediate regime obtained from the spatial variations and MSD, respectively,good agreement is obtained. This suggests that the hydrodynamic interactions dramatically change the self-diffusions of ellipsoids in narrow channels. These findings have important implications for the research of the microfluids for cell culture,drug delivery,etc.