刘 剑， 王恩荣， 颜 伟， 张海龙

(南京师范大学 电气与自动化工程学院，南京 210042)

磁流变阻尼器(Magneto-rheological Damper, MRD)作为新型智能控制器件，其输出阻尼力可通过调节直流驱动电流来改变，并且具有半主动可控、体积小易安装、功耗低、安全可靠等优点，在结构振动半主动控制领域具有广阔的应用前景，受到了国内外学者的广泛关注[1-5]，例如建筑结构抗震[6]、MR半主动悬架系统[7-9]、军用弹射器后座减震[10]等应用研究。

然而，有关MRD的成果大多局限于理论和实验阶段，原因在于其内部的磁流变液存在严重的滞回非线性及饱和特性[11]，此外，工程中的真实动力系统几乎总含有各种各样的非线性因素[12]，增加了精确控制的难度并可能引起系统产生不可预测的动力学行为。以车辆MR悬架系统为例，车辆本身就包含有多种非线性元件，研究人员也一直在进行相关非线性特性分析与控制研究，Dai等[13]建立了车辆四轮转向非线性模型，通过分析平衡点的稳定性发现了系统Hopf分岔行为；Marek等[14]考虑了悬架弹簧的非线性特性，用多项式模型描述的弹簧刚度建立起悬架系统，利用Melnikov理论建立了系统全局分岔集，进而发现了系统的非线性运动特性；Siewe[15]采用悬架阻尼力的多项式模型，对单频正弦路面激励下的单自由度(Degree of freedom, DOF)车辆悬架的混沌运动进行研究，分析了简谐路面下的亚谐共振；Litak等[16]基于Yang的研究模型，应用Melnikov理论讨论了全局同宿轨道分岔，确定了产生混沌运动路面激励幅值的阈值。也有少量研究针对MR悬架系统的非线性动力学分析，Albert 等[17]基于实验下的MRD分段线性模型，建立了1-DOF MR悬架系统，并运用不连续系统动力学理论和映射技术进行了系统分岔与稳定性分析；Wu等[18]采用模式辨识得到MRD动力学模型，得到了MR悬架系统的频率响应，揭示了系统的分岔特性以及幅值变化通向混沌的途径，但未考虑关键的激励频率影响；黄苗玉等[19]采用MRD的Sigmoid模型分析了MR悬架系统非线性动力学特性，得到了系统由倍周期分岔通往混沌的路径，但其采用的Sigmoid模型由于动态特性不理想，正逐步被Bouc-Wen模型所取代。

上述研究成果一定程度上揭示了MR悬架系统在路面激励下出现混沌运动的可能性。在前人的基础上，作者进一步提出了修正的Bouc-Wen现象模型，对某商用MRD进行了参数辨识，建立典型的2-DOF MR悬架系统动力学模型，理论推导出系统存在混沌运动的可能性，进一步结合悬架系统的实际运行工况，在路面激励通频带内，分析了系统的动力学行为演变过程。提出了基于理想运动状态追踪的滑模控制器，将系统控制到理想的周期运动状态，有效地抑制了由于MRD滞回非线性导致的混沌运动，同时一定程度上兼顾了悬架性能。本文研究内容对于工程应用中的复杂非线性系统的动力学特性分析与控制提供了参考。

1 修正的Bouc-Wen滞回F-v模型

建立精确实用的MRD动力学模型是对其进行控制的关键，由于MRD中磁流变效应的复杂性，目前还没有公认的MRD动力学模型，最早是Shames等研究的Bingham模型，简单易分析但不能描述前屈服特征，即双黏性特征、滞后特征和剪切变稀现象。为了能描述阻尼器的滞后特征，很多学者又研究了各种模型，比较有效的模型有Spencer等[20]提出的Bouc-Wen模型和基于Bouc-Wen的现象模型[21]，Choi等[22]提出的多项式模型。图1所示为典型的Bouc-Wen现象模型，它准确地描述了MRD固有滞回非线性特性，但是由于模型中的线性项只是计算了输出阻尼力与控制电流的关系，因此不能很好地描述在直流驱动下MRD表现出来的对磁场的非线性和饱和响应特性。作者引入Sigmoid函数提出了改进的Bouc-Wen现象模型，该模型通过将电流调制与滞回特性解耦分离，有效地解决了上述问题，模型表达式为

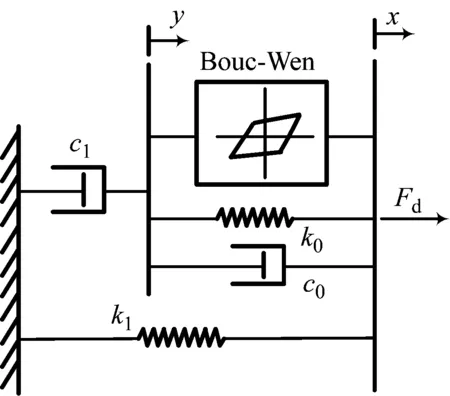
图1 Bouc-Wen现象模型结构

Fd=f(id)=c(id)Fh(xr,vr), 0≤id≤Im

(1)

(2)

(3)

xr=xs-xu,

(4)

式中：id和Im分别表示MRD直流驱动电流以及最大驱动电流；c(id)为基于Sigmoid函数的驱动电流调节函数，准确地描述了对驱动电流的非线性饱和响应特性，c(id)≥1，当驱动电流id=0时，c(id)=1；xr、vr表示阻尼器活塞行程位移和速度，Fh(vr)用来描述当id=0时即在被动方式下MRD输出阻尼力与活塞的动行程速度vr之间的滞回关系，x表示活塞动行程，y和z为无量纲内变量。k0,k1,k2,a0,I0,α,β,γ,c0,c1,n,A,x0为模型中的待定常数。

对商用CARRERA MagneShockTM MRD进行模式辨识，驱动条件为直流12 V，最大电流Im=0.5 A。如图2(a)所示的实验环境，振动台输出为单频正弦激励(幅值、频率为： 0.01 m, 1.5 Hz；0.025 m, 1.5 Hz； 0.01 m, 5 Hz；0.025 m, 5 Hz；0.005 m, 10 Hz)，分别在0、0.1 A、0.2 A、0.3 A、0.4 A驱动电流下测得F-v曲线，进一步利用非线性最小二乘法对上述Bouc-Wen模型进行参数识别，得到k0=184.1,k1=1 528.1,k2=10.092,a0=7.526,I0=0.069,α=20 373.7,β=233 849.1,γ=8 816.9,c0=1 368.7,c1=6 222.7,n=2,A=20.6,x0=-0.004[23]，图2(b)分别比较了幅值、频率分别为0.025 m, 1.5 Hz时的实验结果与辨识模型计算结果，显然辨识出的模型能够准确地描述MRD。

由图2可知，MRD具有强滞回非线性特性，其输出阻尼力对电流和频率有强依赖特性，不同的输出电流、不同的激励频率下，其F-v特性有明显变化。在实际工程应用中，MRD的非线性动力学特性不能忽视。

2 MR悬架的非线性动力学行为分析

2.1 系统的力学模型与运动微分方程

图3所示为2-DOF车辆MR悬架系统结构示意图，主要包括车身、悬架弹簧、MRD和车轮等部件，其中仅考虑MRD的非线性因素，对其它部件近似线性化。ms和mu分别表示簧载质量和非簧载质量，ks,id和Fd分别表示悬架弹簧弹性刚度、MRD驱动电流和输出阻尼力，kt和ct分别表示轮胎等效刚度和阻尼系数。xi表示路面输入激励。xs和xu分别表示簧载质量、非簧载质量的垂直振动位移[8]。根据牛顿第二定律建立的力学模型为

(a) MRD参数识别实验系统

(b) 模型计算结果与实验数据比较

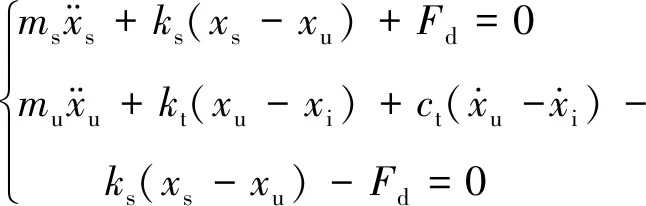
(5)

图3 2-DOF MR悬架结构示意图

为了便于计算，选取新时间常数τ=ωt，ω2=ks/ms，将上述MR悬架系统化作无量纲形式[24]

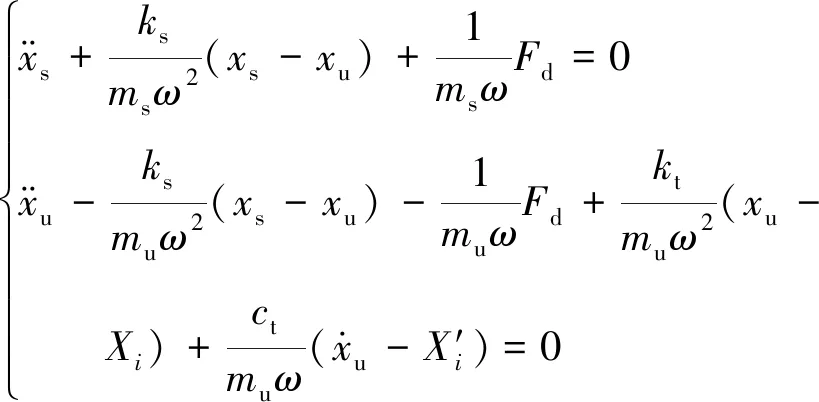
(6)

式中，Xi为无量纲化的路面激励。

D0={(x1,x2,x3,x4,x5,x6)αx6+c0(x2-x4)+

k0(x1-x3-x5)<0∩x6<0}

D1={(x1,x2,x3,x4,x5,x6)αx6+c0(x2-x4)+

k0(x1-x3-x5)0∩x60}

D2={(x1,x2,x3,x4,x5,x6)αx6+c0(x2-x4)+

k0(x1-x3-x5)0∩x6<0}

D3={(x1,x2,x3,x4,x5,x6)αx6+c0(x2-x4)+

k0(x1-x3-x5)<0∩x60}

取定分析系统零输入情况令Xi=0，结合式(1)～式(6)得到系统运动微分方程为

a65x5+a66x6)

(7)

其中，

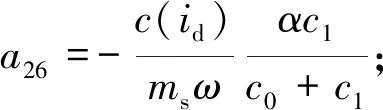
当x∈D0∪D1,B=-β-γ, 当x∈D2∪D3,B=-β+γ。

2.2 系统平衡态及其稳定性分析

选取系统参数簧载质量ms=562.5 kg，非簧载质量mu=90 kg，悬架刚度系数ks=57 000 N/m，轮胎刚度系数kt=285 000 N/m，轮胎等效阻尼系数ct=100 N/(m·s-1)，MRD模型参数采用前文辨识结果，暂不考虑MRD半主动控制，固定id=0.5 A，则c(id)为常数。令式(7)左边为0，求系统的平衡点，用X=(x10,x20,x30,x40,x50,x60)表示，计算得到系统唯一不动点X0=(0,0,0,0,0,0), 其稳定性由系统在X0处的雅可比矩阵特征方程决定

J=

(8)

计算得到特征值为λ1=-1.517 6+2.391 3i,λ2=-1.517 6-2.391 3i,λ3=-0.009 9+0.205 7i,λ4=-0.009 9-0.205 7i,λ5=0.005 2,λ6=0,发现λ1和λ2、λ3和λ4分别互为共轭复根，而λ5为正实根，λ6=0，X0是一个不稳定的鞍点，也说明系统(6)的无扰运动是不稳定的，因此具有发生混沌运动的可能。

当考虑施加外部激励时，由于上述6维系统包含绝对值和平方项，针对此类非线性动力学系统无法求出解析解，因此采用数值方法求解。考虑到其工程应用背景，系统运行工况是可以确定的，即车辆正常行驶过程中，悬架系统承受的路面激励频率范围在1～15 Hz，幅值不超过10 cm[25]。本文拟采用单频谐波作为路面激励，xi=Asin(Ωt)，A表示路面幅值，Ω表示路面激励角频率Ω=2πf，无量纲化后得到Xi=Ω2Asin(Ω/ωτ)。在整个路面激励频率范围内，保持激励幅值一定，观察不同频率下系统动力学特性变化情况，采用的分析方法为：①数值计算得到相应参数变化范围内系统的全局分岔图，从分岔图中找出系统对参数的敏感区域，并针对该区域进行混沌特性分析；②结合Lyapunov指数(LE)谱判断混沌运动，同样在相应参数变化范围内，得到悬架系统的全局LE谱图，结合分岔图验证系统的非线性动力学运动特性；③作参数敏感区域的系统相平面，直观地观察系统动力学行为演变过程。

2.3 数值计算结果

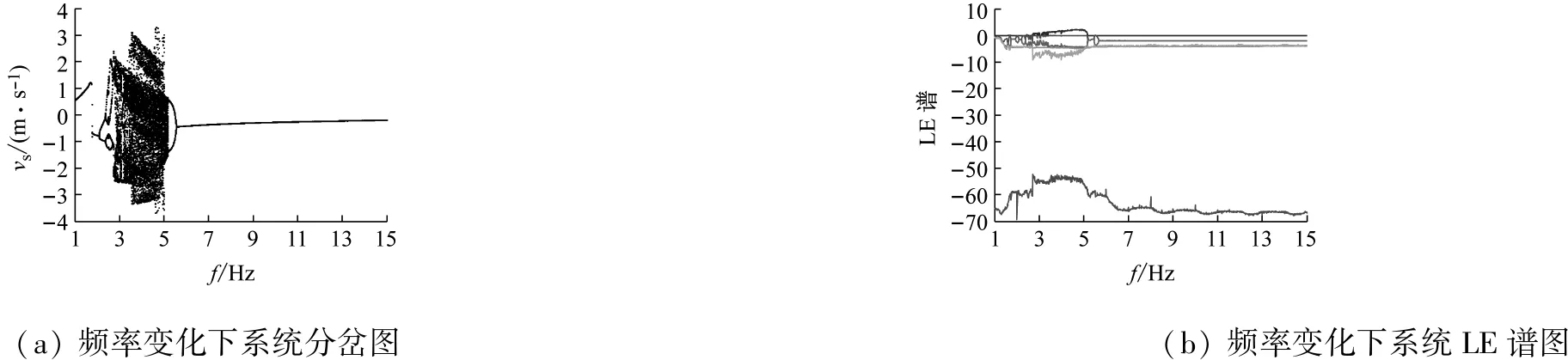
由式(7)建立系统动力学模型，初始值选为X0点。固定输入激励幅值为0.08 m，计算的频率范围为通频带1～15 Hz。求解得到图4所示的通频带全局分岔图，用vs表示簧载质量速度。由图4可知，当频率f∈(1～15)Hz变化时，系统经历了丰富的动力学行为演变，分析时以1～4 Hz为低频区、4～8 Hz为中频区、8～15 Hz为高频区。在高频区域系统出现了稳定不动点，系统表现出良好的稳定性。而在低频和中频区域(f∈(2～6)Hz)，系统经历了非线性动力学行为的变化，尤其是低频2 Hz向中频渐进过度阶段，系统的动力学行为演化过程尤为复杂。结合LE谱可以看出，系统的最大LE在这两个区域都出现了大于零的情况，而在低频f∈(2.75～3.15)Hz区域，连续出现了最大LE在0线附近振荡的情况，在5 Hz附近系统甚至出现了两个LE同时大于零，即可能发生超混沌运动。

(a) 频率变化下系统分岔图(b) 频率变化下系统LE谱图

图4 路面激励通频带全局分岔图与对应的LE谱

Fig.4 Global bifurcation diagram and corresponding LE spectrum for excitation frequency

如图4(a)所示，当分岔参数f=1.76时，系统在固有共振点附近发生了一次跳跃(振幅突变)，但仍然保持了1周期运动。图5进一步给出了系统随f变化分岔图与相应最大LE谱图的局部放大，图5(a)所示当f=2.08 Hz时，系统的1周期运动失稳发生倍周期分岔变成2周期运动，当f∈(2.07～2.488)Hz，随着f的增大，系统2周期运动失稳经由倍周期分岔直至16周期运动，随着f继续增大，结合图5(b)可以看到在f=2.475附近系统短暂进入混沌振荡后经由逆向倍周期分岔演由16周期运动变为8周期至4周期，随后再次经由逆向倍周期分岔至2周期后，由切分岔直接通向了混沌(图6(a)～(e))；如图5(c)所示，当f∈(2.78～5.2)Hz时，系统先后交替出现周期运动、倍周期分岔和混沌运动，发生了鞍结分岔(图6(g)～(i))，结合图5(d)可以看到，在鞍结分岔点左右的最大LE明显是异号的；如图5(c)所示随着f继续增加，系统进入混沌区域，并伴随有阵发混沌；当f∈(5.151～5.53)Hz时，系统经由逆向倍周期分岔从混沌运动状态返回到周期运动(图6(j)～(l))。

(a) f=2.00～2.75 Hz 分岔图

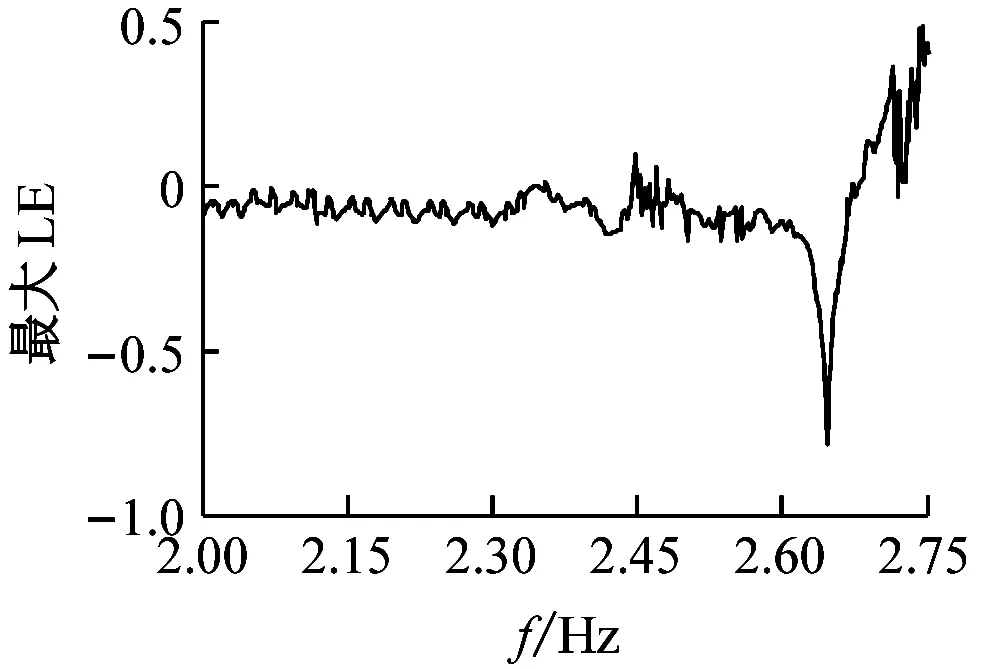
(b) f=2.00～2.75 Hz 最大LE图

(c) f=2.75～6.00 Hz 分岔图

(d) f=2.75～6.00 Hz 最大LE图

图5 全局分岔图与最大LE图的局部放大

Fig.5 Enlarged bifurcation diagram and maximum LE diagram

为了更加直观地考察系统动力学演化过程，图6给出了几组典型频率f下的系统相平面图，可以看出在f∈(1.5 Hz→2.2 Hz→2.39 Hz→2.425 Hz→2.488 Hz)时，系统经过不断地倍周期分岔先后从1周期变为16周期运动(图6(a)～(e))；紧接着随着f继续增加，系统进入逆向倍周期阶段，从16周期运动逐渐变为2周期运动，最终在f=2.745 Hz处由2周期直接进入混沌区域(图5(a)，6(f))；随着f的增加，在f∈(3.03 Hz→3.12 Hz)时，系统经由鞍结分岔脱离混沌吸引子至5周期运动(图6(g))，短暂停留后经由倍周期分岔，以收缩的方式再次进入新的混沌区域(图6(h)～(i))；当f5.15 Hz时，系统从混沌区域脱离由逆向倍周期分岔从4周期逐渐稳定到1周期运动(图6(j)～(l))。

(a) f=1.5 Hz

(b) f=2.2 Hz

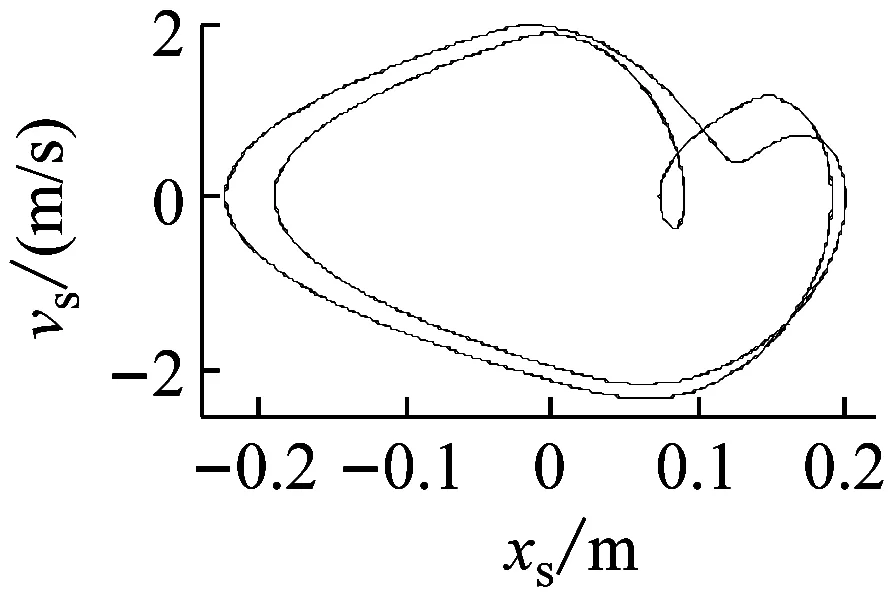
(c) f=2.39 Hz

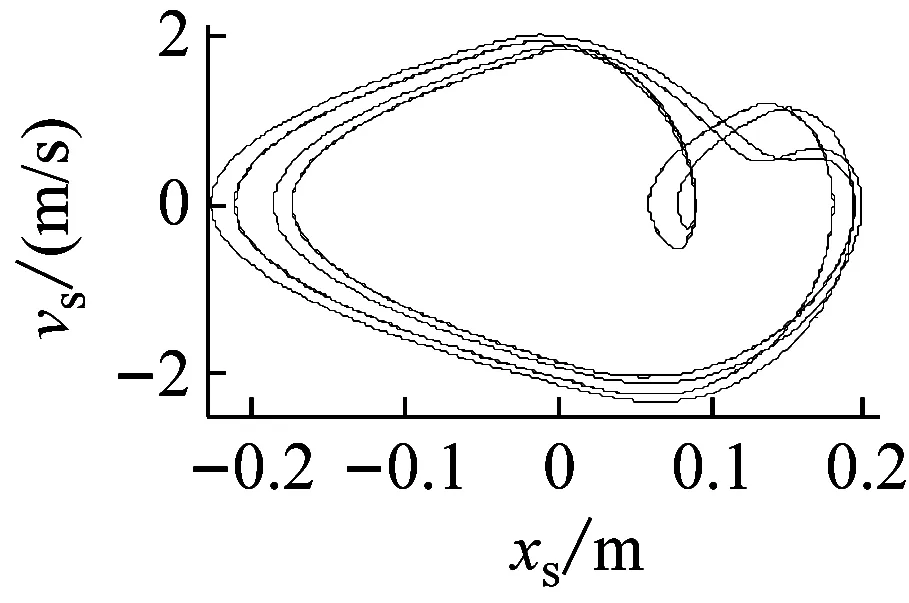
(d) f=2.425 Hz

(e) f=2.488 Hz

(f) f=2.8 Hz

(g) f=3.035 Hz

(h) f=3.071 Hz

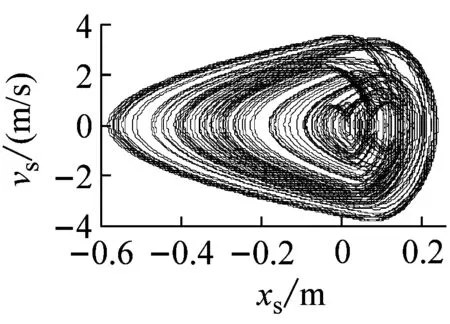
(i) f=3.75 Hz

(j) f=5.17 Hz

(k) f=5.442

(l) f=6 Hz

图6 不同频率f下的相平面图

Fig.6 Phase plane for different frequencyf

由图6可知，在f变化过程中系统存在混沌运动，系统通向混沌运动的路径可能是倍周期或者逆向倍周期分岔，同时也伴随着着鞍结分岔和阵发混沌现象。这与上一节的理论分析预测结果相吻合。然而，混沌运动导致系统的运行轨迹不可预测，MRD的控制无法实现甚至导致系统发散失稳，对车辆行驶造成不可预测的危害，因此，需要提出有效的非线性控制方法。

3 非线性系统的滑模变结构控制

由上述分析可以看出，在2.75～6.00 Hz范围内，系统发生的混沌振动导致簧载质量垂直速度幅值急剧增加，极大地影响了车辆悬架驾乘舒适性，需要进行有效的混沌振动抑制。滑模变结构控制是针对非线性系统控制的有效方法[26]，图7(a)和(b)分别给出了MR悬架系统和理想线性参考模型的结构，本文提出的非线性系统滑模控制器(SMCC)设计是通过使被控系统ms追踪参考模型ms0的运动来实现，渐近稳定滑动模态在实际被控系统和参考模型间的动力学误差中产生。

(a) 2-DOF MR车辆悬架子系统(b) 理想线性系统

图7 MR悬架系统和理想线性参考模型的结构

Fig.7 Structure of the MR suspension system and ideal linear reference model

3.1 滑模面设计

在作为参考模型的图7(b)所示的1-DOF线性参考模型，其动力学方程表示为

(9)

式中，ms0是参考簧载质量，cs0是线性天棚阻尼系数，xs0是簧载质量垂直位移，c0和ks分别是线性阻尼系数和弹簧刚度。

对于图7(a)所示的2-DOF MR悬架子系统，定义滑模面s为

(10)

式中，λ0为滑模面的收敛速率，es(t)=xs(t)-xs0(t)为实际被控系统和参考系统之间的动力学误差，当t趋于无穷大时，e(t)=0。

3.2 滑模控制器设计

(11)

式中，φ是正常数。由式(6)得

(12)

结合式(10)得

(13)

(14)

应用比例切换控制策略，定义控制器输出u为

u=u0-Ksgn(s)

(15)

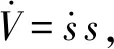
(16)

进一步代入式(15)得

(17)

结合式(14)和(17)，化简得

(18)

进一步整理为

(19)

由式(14)得

(20)

将式(20)代入式(19)得

(21)

根据滑模控制的Lyapunov稳定条件，将式(21)代人式(11)，得

(22)

根据|s|=s·sgn(s)化简上式得

(23)

由于实际车辆负载是变化的，定义ms0=ms，β为受控簧载质量对于参考簧载质量的变化率，则β=ms/ms0≥1。选取滑模控制增益K为

K=-ms0βφ-(β-1)(|u0|+ks|xs|+ks|xu|)

(24)

至此，已推导出了基于运动状态追踪的滑模控制器。进一步地，为避免系统产生颤振，采用饱和函数sat(s)来代替在式(24)中符号函数sgn(s)，在|s|≤ε和|s|ε时分别取值sat(s)=s/ε和sat(s)=sgn(s)，这样式(24)可改写为

u=u0-Ksat(s)

(25)

式中，ε为正常数。

3.3 滑模控制器稳定性证明

下面证明所设计的滑模控制器能确保系统滑模面趋于渐近稳定。将式(24)代入式(21)得

(26)

进一步整理得

(27)

当s≥0时，式(27)改写为

(28)

3.4 控制结果

用于追踪控制的理想参考模型参数为cs0=500 N/m·s-1,c0=2 500 N/m·s-1,ks=57 000 N/m，滑模控制器的主要参数取值为：λ=1.5、β=1.5、φ=0.05、ε=1。为验证控制效果，在f=5 Hz,A=0.08 m时，观察控制效果，图8所示为控制前后簧载质量位移、速度的时序图，控制器在10 s投入，可以看出，切入控制以后经过0.3 s调整时间，系统响应时间序列变为为整齐且周期性变化的波形图，提出的滑模控制器有效抑制了原有的混沌运动，控制后的MR悬架表现为稳定的周期运动。图9所示为控制下的系统全局分岔图，对比图(4)可知，提出的控制器在通频带内有效抑制了原系统中频带内的混沌运动，同时也并未改变其他区域内的运动特性。图10进一步给出了控制前后的悬架性能比较，以簧载质量加速度均方根值aws表示驾乘舒适性，以非簧载质量加速度均方根值awu表示操控稳定性，可以看出，控制后在0.5～15 Hz范围内aws和awu均小于控制前，除了0.5～0.6 Hz处控制后的aws略有增加，控制后的悬架系统第一共振点附近aws显著降低，第二共振点附近awu显著降低，表明该控制器同时一定程度改善了悬架性能。

图8 滑模控制前后的系统时序图比较

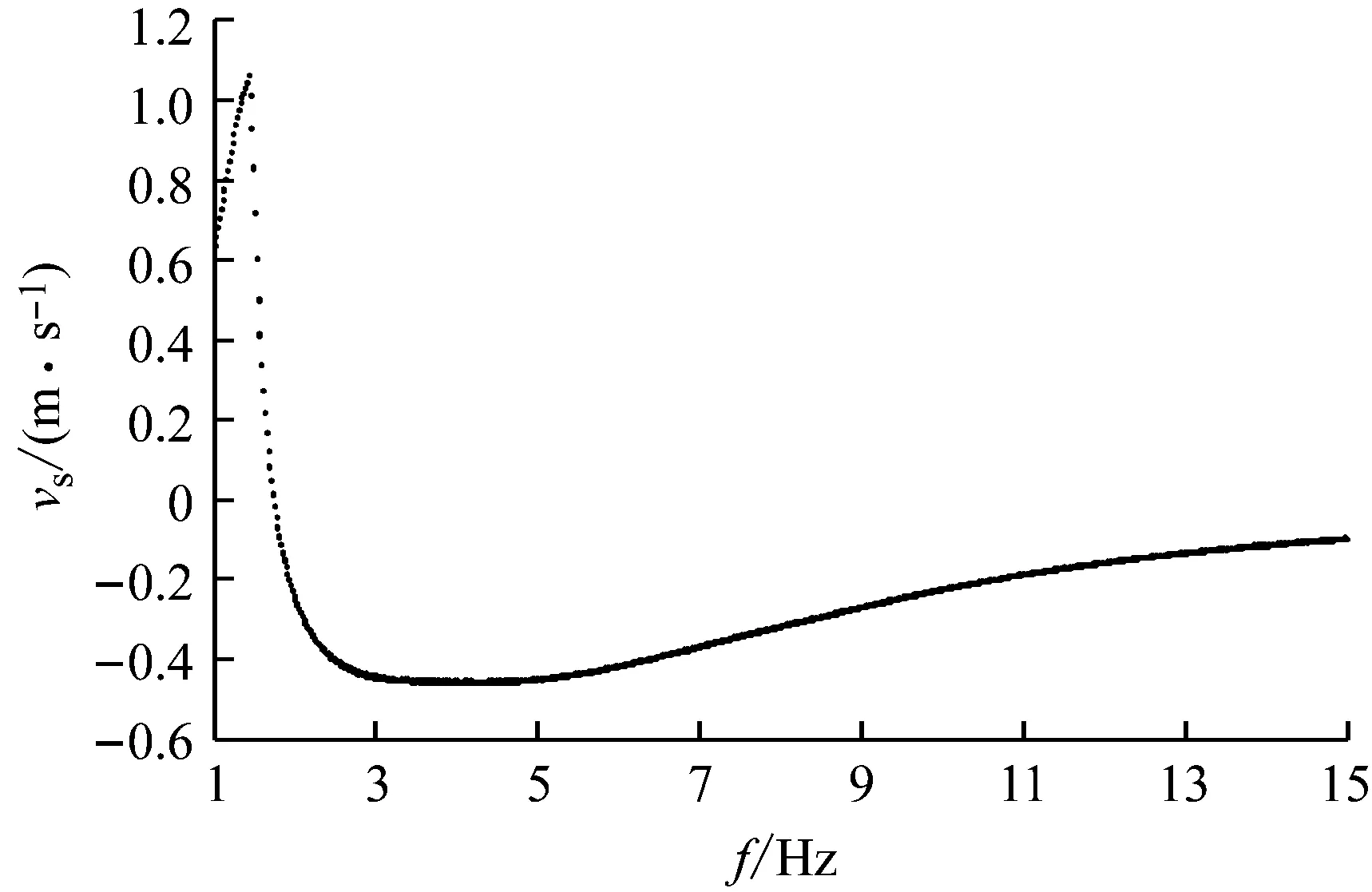
图9 滑模控制后的系统全局分岔图

4 结 论

(1) 研究了MRD在实际应用中的非线性动力学问题，基于修正的Bouc-Wen现象模型对实际MRD进行参数识别，建立了2-DOF磁流变车辆悬架系统。在零输入条件下，根据系统不动点处的雅克比矩阵特征值预测了系统存在混沌运动的可能，并在单频谐波激励下，通过数值方法得到了系统全局分岔图和LE谱图，分析了路面激励参数变化下系统的动力学演化过程，发现在中频段区域，系统经过倍周期分岔、切分岔和逆向倍周期分岔先后发生了周期运动、阵发混沌运动和周期运动。

(2) 根据理想参考模型，设计了基于运动状态跟踪的滑模控制器，有效地抑制了系统的混沌运动，将原有的混动状态镇定到稳定的周期运动。该研究对MR车辆悬架系统相关参数设计以及MRD其它应用研究提供了理论依据，也为实际工程应用中的非线性系统动力学分析与控制方法提供了参考。

(a) 簧载质量加速度均方根值频谱特性

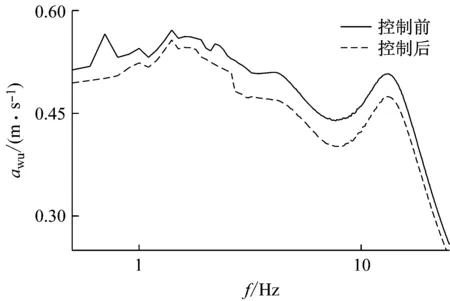
(b) 非簧载质量加速度均方根值频谱特性