黄迪山， 刘 成， 张 波

(上海大学 机电工程与自动化学院，上海 200072)

由于系统参数(质量、阻尼和刚度)的周期时变性，许多系统的动力学建模可以采用周期系数的二阶微分方程组描述，这在力学上被称为参数振动系统。参数振动系统的稳定性、响应预测和控制策略是研究参数振动的基本问题。在以往对参数振动稳态响应求解的研究中，常用解析方法有Hill法[1]、摄动法[2]、平均法、Floquet理论[3]、Sinha Chebyshev多项式法[4]等。另外对参数受迫振动响应的计算方法，还包括David等的传递矩阵法[5]、Floquet特征向量的线性组合[6]、改进的直接谱分析法[7]，IHB法进行非线性振动求解，多尺度法求振动响应[8]等。

对于参数系统定性、定量分析，以上方法虽然取得了重要进展，但是大多数方法对系统响应逼近不能完全地进行解析分析，导致一些非线性动力学特征仍然有可能被隐藏。在科学和工程应用中，用傅里叶级数表示的响应在故障识别与诊断、结构健康监测中十分便捷。尤其是在对横向裂纹转子、齿轮啮合的周期性刚度问题，参数振动响应的三角级数逼近是非常重要的[9]。

为了证实线性参数激励系统的理论结果，Han等[10-11]和Chen等[12]开发了受电磁刚度激励的悬臂梁，观察到参数振动的自由响应，验证了自由响应谱是由固有频率、及一系列固有频率与参数频率线性组合的重要动态特性。

调制反馈[13]模型成功地应用于参数振动受迫响应，给出了外界激励和参数激励共同作用下的响应。Huang等[14]给出了单自由度参数振动自由响应的三角级数逼近。本文将利用调制反馈分析法，讨论二自由度参数振动的自由响应求解，并得出简明的结论。本文所提出的矩阵三角级数逼近法是将调制反馈概念，从单自由度拓展到二自由度参数振动系统，引入归一化模态，计算得到参数振动模态以及系数矩阵，系数矩阵事实上是谐波组合共振时的衍生模态。当调制指数足够大时，衍生模态的影响不可忽略。

1 自由响应形式

对二自由度的刚度参数周期激励系统，其动力学方程为

(1)

(2)

式(2)将二自由度的参数振动问题演变为图1所示的一个含调制单元的反馈系统。该系统是由一个二自由度线性系统和一个调制环节组成。系统的输出X(t)是所关注的参数振动自由响应。

图1 调制反馈系统示意图

对二自由度刚度周期激励系统的自由响应而言，每个振荡频率ωsi(i=1,2)都将产生频率裂解现象(见图2)，系统将瞬间裂解出无穷多个频率组合分量。

图2 系统频率裂解瞬间过程示意(t≥0,Δt→0)

因此，系统自由响应是主振荡频率ωsi和参数激励频率ω0的一系列线性组合，其自由响应表示为以下矩阵三角级数

X(t)=X1(t)+X2(t)=

(3)

由于反馈回路存在，系统主振荡ωsi与固有频率ωni是不相等，但主振荡频率ωsi分量分布在系统固有频率ωni的附近；从总体上说，由于二自由振动系统中的模态具有低通滤波的功能，当系数k→∞时,谐波成分矩阵Ck→0、Dk→0。因此，二自由度参数振动自由响应的求解问题就转化为式(3)中系数矩阵Ck、Dk和主振荡频率ωsi(i=1,2)的确定。

2 响应解确定

2.1 主振荡频率ωsi

应用欧拉公式cos(ω0t)=(ejω0t+e-jω0t)/2，式(1)可转化为

(4)

设式(4)的解为

(5)

式中:Ek为2×1矩阵。

将X(t)代入式(4)，整理得：

(6)

对式(6)应用谐波平衡，可以得到无穷多个由系数Ek组成的线性方程

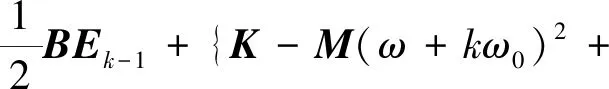
(7)

(k=-∞,-n+1,…,-1,0,1,…,n-1,∞)

引入记号

(8)

Ωk=K-M(ω+kω0)2+jC(ω+kω0)

(9)

将系数Ek组成的线性方程组装在一起，形成无穷阶的线性代数方程组, 称裂解协调代数方程组。当阶数取2n+1时，方程表达为

(10)

当n→∞时，系数矩阵E-n-1→0和En+1→0。因此，将等式(10)记作

W1E=0

(11)

式中:W1为一个复分块矩阵。齐次方程(11)若要有解，充要条件是矩阵W1行列式等于零，则特征方程

det(W1)=0

(12)

对于二自由度参数振动系统，存在复根ωi=ωsi+jδi，ωsi为主振荡频率，δi为衰减因子。

特征方程式(12)求解可获得4×(2n+1)个根。由于主振荡频率主要集中在系统固有频率ωn1,ωn2附近，考虑反馈环节影响，从特征方程所求得的根值中选取接近于并小于系统第i阶固有频率ωni的值作为主振荡频率ωsi(i=1, 2)。

同理设：

(13)

其中Fk为2×1矩阵，将式(13)的X(t)代入式(4)，得到与式(7)类同的谐波平衡方程，将系数Fk组成的线性方程组装在一起，可得到式(14)

(14)

令：

det(W2)=0

(15)

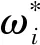
2.2 系数矩阵

系数矩阵C0和D0是与振荡模态有关的复矩阵。矩阵C0和D0是2×2阶矩阵。

在式(10)中

其中r1是向量(Γ12Γ22)T,r2是向量(Γ21Γ22)，r3是向量(Γ11Γ21)T。

设归一化模态

(16)

因此，求得模态矩阵C0和系数矩阵Ck为

(17)

(18)

通常系数矩阵Ck是一个复矩阵。

矩阵Dk和Ck具有相同的求解过程， 可求得模态矩阵D0和系数矩阵Dk为

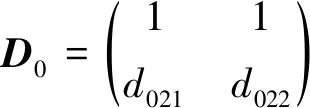
(19)

(20)

矩阵Dk与矩阵Ck互为共轭。

2.3 方程通解

在求得ωi(i=1,2),系数矩阵Ck，Dk(k=-n,-n+1,…,-1,1,…,n-1,n)，则自由响应通解可以表示成：

(21)

式中:p1,p2,q1,q2为任意常数。

2.4 初始条件

设参数振动初始条件为

X(0)=[x1(0)x2(0)]T

(22)

(23)

将初始条件式(22)和式(23)分别代入式(21)得到

(24)

X′(0)

(25)

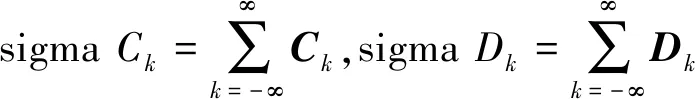
式(24)和式(25)可写成

(26)

(27)

可得出p1,p2,q1,q2

(28)

3 数值算例与结果分析

3.1 耦合倒立双摆系统自由响应模型

在直升机前行运动中，其旋翼叶片会不断受到时变的载荷力及力矩的作用从而引起参数振动问题。针对直升机机翼的动力学模型，Sinha等[15]进行了简化处理，建立如图3所示的耦合倒立双摆系统模型。

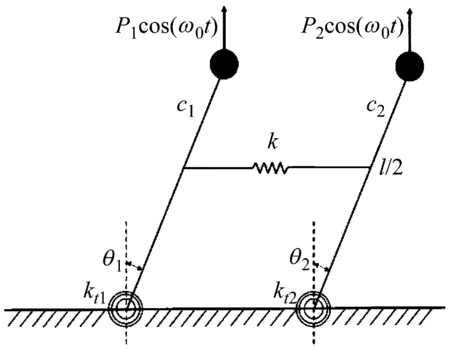
图3 耦合倒立双摆系统

其中双摆与固定基础之间由弹性系数为kt1和kt2的扭弹簧连接，双摆杆中间位置由弹性系数为k的弹簧连接而发生耦合，摆杆转动过程中存在阻尼c1和c2，摆杆顶部存在集中质量m，集中质量位置分别受到时变载荷P1cos(ω0t)和P2cos(ω0t)。此时，该参数振动系统的运动方程为

P1cos(ω0t)lsinθ1=0

P2cos(ω0t)lsinθ2=0

(29)

由于角度θ1、θ2均为小量，计算中可近似sinθ1≈θ1，sinθ2≈θ2。为了便于分析，对式(29)无量纲化，再引入下列参数

式(29)简化的无量纲的微分方程

(30)

对比式(30)，在参数振动方程(1)中设置参数，令ω0=10，β1=β2=0.3。

则系数矩阵

3.2 矩阵三角级数求解

当系统在无参数激励的情况下，得到线性方程的固有频率

ωn1=13.004 0+j0.153 6,ωn2=50.860 7+j0.246 3，

模态矩阵

对式(16)的系数矩阵取47阶方阵(k=-28,…,18)。根据所述计算过程，编制MATLAB程序，得到式(29)的振荡频率

ω1=12.417 9+j0.154 1

ω2=50.644 3+j0.245 9

将ω1和ω2分别代入式(16)， 可得到模态矩阵C0和系数矩阵Ck

同理，求出模态矩阵D0和系数矩阵Dk

令初始条件

(31)

通过式(28)得到p1,p2,q1,q2。

对算例进行自由响应计算，起点为0，设步长0.000 1，总时间10 s，得到参数振动响应的时间历程、频谱和相图,如图4(a)～图4(c)所示。

4 讨 论

4.1 龙格-库塔法

为了验证所述方法，用四阶龙格-库塔法(使用MATLAB ode45)得出的自由响应时间历程、频谱图和相图与矩阵三角级数逼近的结果进行比较。

龙格-库塔法在MATLAB程序仿真中，设置起点为0，步长0.000 01，控制精度为1×10-7，总时间10 s，得到系统自由响应的时间历程、频谱和相图，如图5(a)～图5(c)所示。

通过计算结果对比可以得出，两种方法得出的时域响应、频谱、相图具有高度的一致性。频谱图用于观察自由响应的振荡频率，同时可以清楚地看到由周期参数系统所引起的频率裂解现象。相图用来研究瞬态响应，相图的微小变化可以表征动力学性能变化。从相图可以看出相空间中的波扰动，而这是由于周期参数系统频率的裂解所引起的，即周期参数系统变化导致振荡频率的变化。

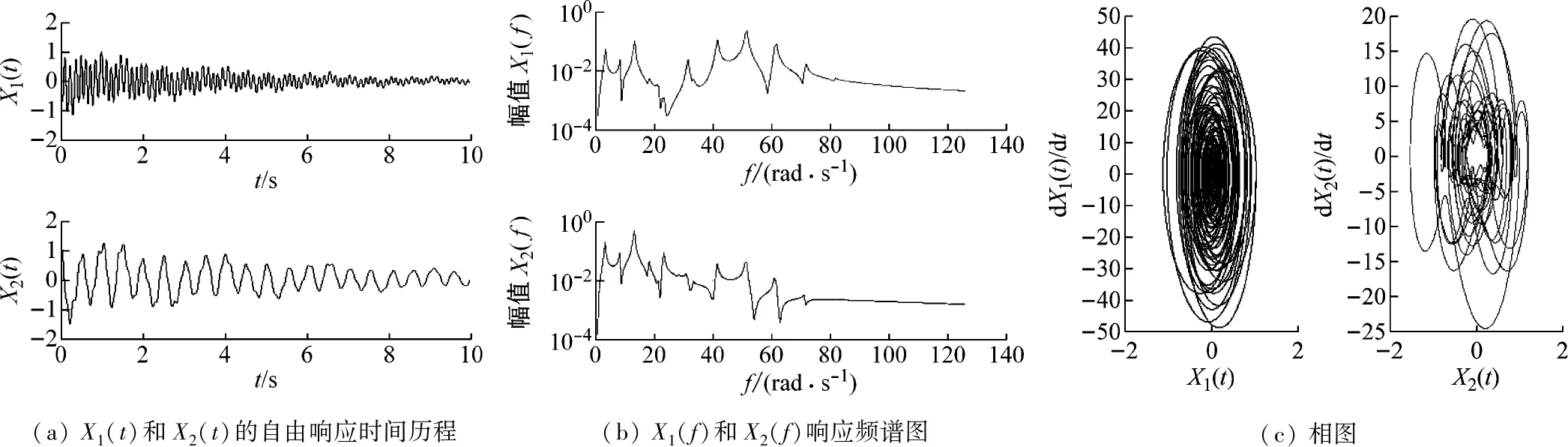
(a) X1(t)和X2(t)的自由响应时间历程(b) X1(f)和X2(f)响应频谱图(c) 相图

图4 矩阵三角级数逼近的振动自由响应

图5 龙格-库塔法得到自由振动响应

Fig.5 Free response simulated by Runge-Kutta algorithm

4.2 计算误差

为了更精确地评价上述两种方法的准确性，引入偏差矢量ε

(32)

针对二自由度系统，ε=[ε1ε2]T，εr表示最大误差的均方根值，即

(33)

式中:εrms1和εrms2为x1和x2的最大误差值。

在给定的例子中，系数矩阵采用了47项(k=-28,…,18)，计算得出的最大有效误差值εmax1=5.380 7×10-12。而龙格-库塔法得出最大有效误差值为εmax2=2.402 3。表1所列为两种计算方法的计算误差和计算所需时间对比。本文方法能提供很高的计算精度，但是计算所需时间多于龙格-库塔法。本文方法的计算时间取决于所设的级数项数的多少。若要减少计算时间，在达到精度要求的前提下，可减少级数项数实现。

表1 两种计算结果的比较

本文的逼近方法相比龙格-库塔法计算误差小。当逼近项数增加，计算误差减小；当项数增加到一定值时，计算误差将达到稳定，且精度趋于定值， 造成此现象的原因可能是本文方法的截断误差或MATLAB计算后的舍入误差所致,如图6所示。

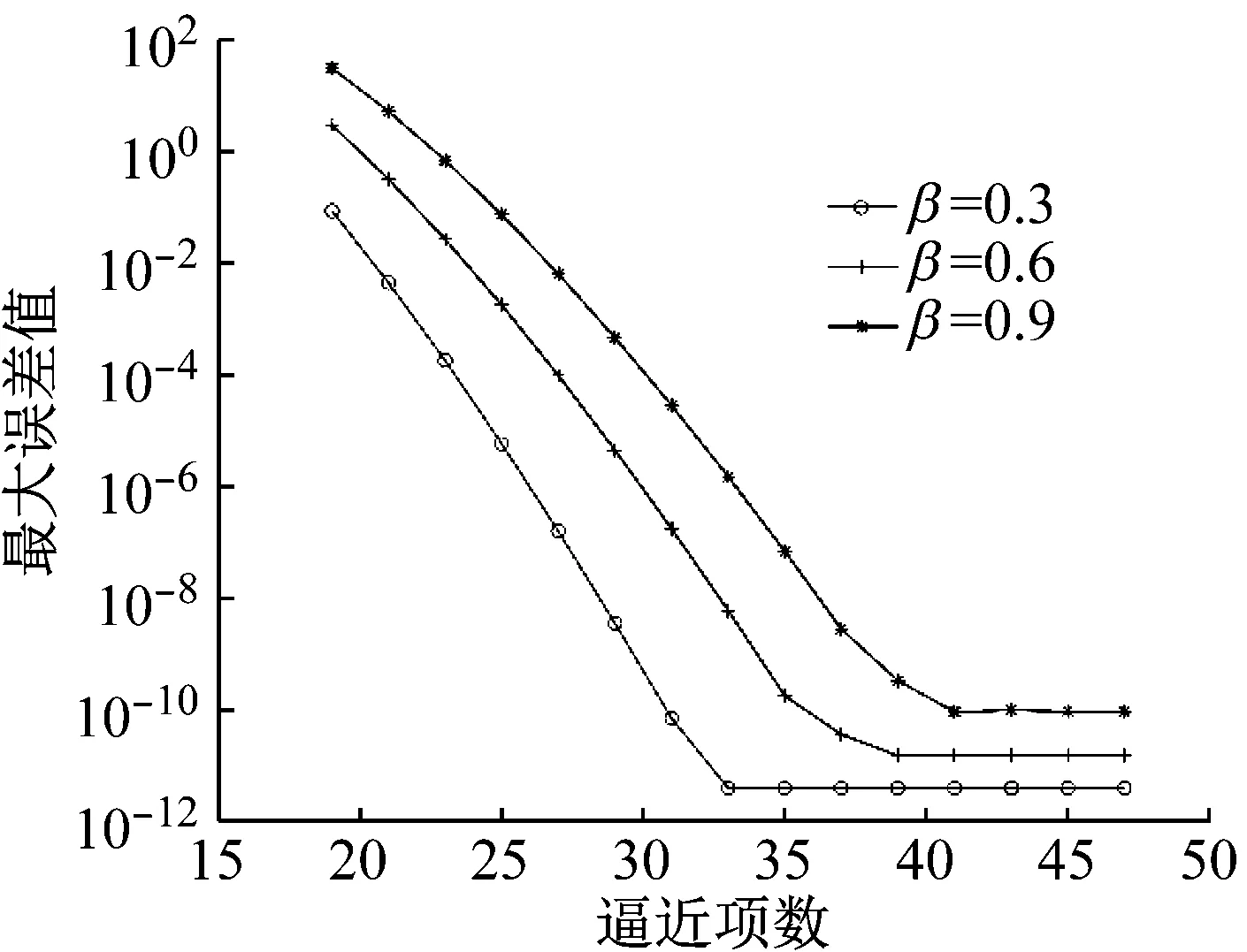
图6 级数项数对计算误差的影响

4.3 调制指数影响

4.3.1 主振荡频率

自由响应中主振荡频率ωs1和ωs2与调制指数β1,β2以及阻尼系数ξ有关,令β1=β2=β，① 若β=0，系统的振荡频率即为系统的含阻尼的固有频率；② 当调制指数β不大时，系统的主振荡频率的减小趋势不大，在工程应用中，可以将含阻尼的固有频率替代振荡频率用于系统参数估计；③ 当调制指数β比较大时，系统的主振荡频率明显减小，β的影响不能被忽略；④ 阻尼系数ξ对主振荡频率大小有影响。当调制指数β一定时，ξ增大，则主振荡频率ωsi(i=1,2)减小。如图7所示。

(a)

(b)

图7 调制指数和阻尼系数对主振荡频率的影响(β1=β2=β)

Fig.7 Effect of index and damping ratio on principle oscillation frequencies (β1=β2=β)

4.3.2 模态矩阵

在β1=β2=0时,参数系统的模态矩阵C0和对应的线性系统的模态矩阵P相等；在β1,β2发生变化时，模态矩阵C0会随着β1和β2的不同而改变，如表2所示。

表2 二自由度参数系统的模态矩阵C0

5 结 论

应用调制反馈分析，给出二自由度参数振动系统的自由响应的矩阵三角级数通解，并以耦合倒立双摆系统为例，计算了二自由度参数振动的自由响应解，得到如下结论：

(1) 自由响应的频率是主振荡频率、一系列主振荡频率和参数频率的线性组合，它们是ωs1+kω0和ωs2+kω0(k=-∞,-n+1,…,-1,0,1,…,n-1,∞)。参数振动系统中，组合频率将产生谐波组合共振。

(2) 当调制指数β1=β2=0，参数系统的模态与对应的线性系统模态相同；当β1,β2发生改变时，模态将会发生改变；自由响应频谱和相空间中的特性可以说明参数系统频率裂解的非线性特性。

(3) 矩阵三角级数逼近法的计算精确度取决于系统矩阵的项数。当系数的项数增加，计算精度越高；调制指数大，逼近项数需增加；当项数增加到一定值，计算误差达到稳定，而且小。

(4) 解出的系数矩阵即为衍生模态矩阵，即谐波组合共振时的振动模态。当调制指数增大时，参数振动的衍生模态不能被忽略。

(5) 阻尼系数ξ对系统的主振荡频率ωsi(i=1,2)的影响较大，ξ增大，则主振荡频率减小。

本文提出的矩阵三角级数逼近法成功地解决了二自由度参数自由振动解问题，并且通过类似方法可以求解多自由度或更高维的参数振动系统，这为解决多自由度参数振动问题提供了一个新的思路。但是，所提出的方法不适用于描述时域中的不稳定响应情况。

致谢感谢美国奥本大学教授S. C. Sinha对本研究的指导和帮助。