陈太聪， 张 奇

(华南理工大学 土木与交通学院 亚热带建筑科学国家重点实验室，广州 510641)

在结构的动力效应评价中，动位移和速度是关键指标之一，如场地地震位移、结构振动变形是评价结构抗震性能的重要参数[1-2]，速度响应也常用于结构阻尼评定[3]。而振动测试实践中，通常直接测量的是振动加速度信号，而非动位移和速度信号，此时可通过对测试得到的加速度时程进行时域积分获得位移和速度时程。但由于测量加速度往往带有一定程度的噪声干扰，导致时域积分得到的速度和位移会产生较大漂移，与真实响应相差甚远。Pintelon等的研究[4]表明，采用Newton Cotes型积分公式的传统时域积分难以获得相对准确的速度或位移，而若采用四阶Runge Kutta方法等高阶积分算法，干扰噪声会引起更大的误差。因此如何由带噪声的加速度信号得到较为准确的速度和位移信息，一直是人们所关注的问题。

已有积分滤噪方法可以分为时域法和频域法两大类[5]。时域法中较具代表性的是多项式拟合去除趋势项法，如陈为真等[6]将该方法用于纠正含直流分量的加速度积分响应，积分滤噪效果明显，但顾名坤等[7]的数值试验表明，在加速度受到复杂噪声影响时，采用该法积分所得的响应效果不理想。因此，针对振动测试实践中的复杂干扰环境，工程实际中更多采用的是频域积分滤噪方法，典型的方法包括数字滤波法、低频衰减法和频率截止法等。

缪惠全等[8]采用数字滤波法对加速度积分所得速度和位移进行校正，可取得较好效果，但滤波的同时会造成各频率成分的相位失真，得到的响应在时间上有延迟现象，需做相位纠正。

胡玉梅等[9]在低频衰减算法中引入目标频率和积分精度两个参数，兼顾了趋势项误差控制和有效信息保留，但积分精度参数的取值需要多次调试。

Brandt等[10]通过对不同积分方法的对比研究，将频率截止法作为最佳积分滤噪方法之一推荐应用。该法操作简单，直接将带噪加速度频域幅值的低频部分做置零处理，相当于理想滤波器去掉低频成分，然后再根据加速度、速度、位移频谱之间的比例关系，由傅里叶逆变换得到对应的时域波形。方新磊等[11]在此基础上，又加入了高频截止滤波，以同时消除低频趋势项和高频干扰噪声。总体上而言，频率截止法易于实现，积分效果优越，但存在对截止频率的设置较为敏感的问题。针对该问题，已有数值研究[12]表明，当截止频率选择在加速度幅值谱的主瓣或旁瓣的波谷附近时，积分得到的位移曲线与实际位移曲线的吻合程度较高，积分误差较小。由此可见，截止频率可参考频谱曲线的形态来近似设置，但较为主观。

实际上，在其它信号处理领域，已有研究通过谱曲线形态的拟合来进行信号特征提取和降噪处理。如李敏等[13]采用高斯曲线拟合光谱曲线的峰形、峰高和峰位等数据，利用拟合得到的特征参量表征光谱信息；李修文等[14]对声发射信号的频谱曲线做平滑处理，最后重构回时域，可以消除有色噪声的干扰。

在上述频率截止法和谱曲线研究的基础上，本文提出一种结合频谱能量形态拟合的频域积分新思路，定义为有效频段法，用于加速度信号的积分滤噪。该方法假设各峰值主频临近区域的频谱曲线符合高斯函数分布，根据该区域内带噪信号的累积能量变化，拟合得到相关函数参数，从而根据三倍标准差原则确定主频有效信息的分布范围，进而通过各有效频段内的频域积分和逆傅里叶变换，重构得到相应的速度和位移信号。文后通过多频简谐激励和随机激励下的数值模拟算例，开展本文方法与频率截止法的对比分析，以检验方法在不同激励下的积分精度和抗噪性能。

1 频率截止法的基本原理

因为本文方法是参考频率截止法的改进研究，因此有必要先简要介绍频率截止法的基本计算原理。

假设按等时距Δt测量得到的带噪加速度信号为X(n)，n=0,1,2,…,N-1，则根据离散傅里叶变换的基本原理，离散的时域加速度信号X(n)可转换为频域内若干离散的频谱信号H(k)，k=0,1,2,…,N-1，其相互转换关系为[15]

(1)

(2)

式中:N为采样数据量;n为时刻点;k为谱线序列点。

频率截止法的基本原理是对频谱中的小于下限截止频率fL和大于上限截止频率fU的频率成分幅值均设置为零，即认为该两部分完全为噪声影响，仅保留两个截止频率之间的信号。该方法可表达为

(3)

式中:Fs=1/Δt为采样频率。

由傅里叶逆变换公式可知，加速度信号在任一频率ωk=2πkFs/N处的傅里叶分量可以表达为

a(ωk,t)=Skejωkt

(4)

式中：Sk为对应a(ωk,t)的谱系数。

当初速度和初位移分量为零时，对加速度信号分量分别进行一次积分和二次积分，可得对应频率ωk的速度信号分量和位移信号分量为

(5)

(6)

最后结合式(1)～式(6)，可得经频率截止后重构得到的加速度、速度和位移信号分别为[16]

(7)

(8)

(9)

最终，频率截止法用于加速度的滤噪和积分滤噪的相关计算流程，可总结如图1所示。

图1 频率截止法的积分流程图

2 基于有效频段的频域积分方法

以上方法在处理含直流分量等低频噪声和机械、电路等引起的高频噪声的加速度信号积分时有较好效果，但工程测量中还会包含如环境干扰等宽频噪声的情况，影响上下限截止频率之间的频率分量，频率截止法无法过滤该部分噪声，最终将影响积分效果。

此时，就有必要采用一定标准，重新甄别有效的频段范围，可能为间隔的若干段，以替代频率截止法中定义的单一频段[fL,fU]，供后续频域积分使用。本文将基于这一思路的频域积分方法称为有效频段法，文中也将通过频谱能量形态拟合的方式来确定有效频段的分布范围。

2.1 分段频谱曲线形态假设

设实测加速度信号X(n)的对应频谱H(k)包含m个峰值主频，按从小到大的顺序依次为f1,f2,…,fm。如此整个频率范围可按如下方式分为m段

(10)

式中:fmax为频谱曲线对应的最大频率，在振动测试中一般取为分析频率，即fmax=Fa=Fs/2.56；或当fm距离Fa较远时，也可近似取fmax=(2∶5)fm，对滤波结果的影响不大。

为了方便后续分析，上述m个频段均进行归一化处理，即都归一化为范围(0,1]。此时，假设每个频段内的频谱曲线符合相应的高斯函数分布[17]

(11)

式中:i=1,2,…,m；x∈(0,1]为每个频段内的归一化频率；参数ai、bi和ci分别代表高斯函数的幅值、中心位置和半径。

基于式(11)定义的频谱分布形态，相应的每一频段内的频谱累积能量分布函数可由下式计算得到，

(12)

式中:erf(·)为误差函数;Ei(x)在形态上表现为反Z型的单调递增函数。

至此，高斯频谱分布函数Gi(x)和频谱累积能量分布函数Ei(x)均可用于后续的参数拟合，以确定高斯函数中的待定参数。但实际计算表明，基于频谱Gi(x)的参数拟合结果不稳定，容易受测试噪声水平波动的影响；而基于能量Ei(x)的参数拟合效果较好，受测试噪声的影响小。因此，本文选用频谱累积能量分布函数Ei(x)来进行参数拟合。

(13)

2.2 分段累积信号能量计算

在第i个归一化频段内，离散的加速度频谱信号的累积能量按下式计算得到

(14)

(15)

2.3 参数拟合与有效频段确定

基于式(15)计算得到的离散数据，用式(13)定义的非线性连续函数进行非线性拟合，迭代收敛后得到参数bi和ci，其中迭代初值可分别取为0.5和0.5。

如图2所示为实际操作中的一个典型例子，显示了某个归一化频段中计算得到的带噪信号离散数据，以及相应拟合得到的频谱累积能量分布曲线和对应的高斯频谱曲线。

根据概率统计理论，高斯分布函数在均值位置左右三倍标准差范围内的数据具有99.73%的保证率[18]，足以表征函数。因此，第i阶主频能量分布的归一化有效频段可按三倍标准差原则取值如下

[bi-3ci,bi+3ci]

(16)

其相应的实际有效频段为

(17)

最终，有效频段法的积分滤噪流程,如图3所示。有效频段法的实现过程与频率截止法基本相同，然而其通过曲线拟合自动确定最佳的频域积分范围，减少了主频之外的噪声干扰。

图2 归一化频段内的频谱能量形态拟合示意

图3 有效频段法的积分流程图

3 数值算例

如图4所示为六自由度悬臂梁结构，考虑竖向振动。其各阶模态阻尼比为0.01，质量阵和刚度阵为

M=diag(4 4 4 4 4 4)×105kg

图4 六自由度悬臂梁结构模型

Fig.4 Structural model of a 6-DOFs cantilever beam

设结构的初始速度和位移均为零，考虑工程中较常见的激励类型，在结构自由端分别施加竖向的多频简谐激励和白噪声随机激励，其中简谐激励取为

z(t)=200sin 6πt+100sin 20πt+100sin 40πt

然后按Newmark-β法求出加速度、速度和位移响应时程，作为精确参考解。在加速度解中分别加入1%、5%、10%、15%、20%和25%的白噪声干扰作为观测加速度。再采用有效频段法得到速度和位移响应，以及修正的加速度响应。这里作为对比，同时采用频率截止法中常用的低频截止进行相关响应的积分求解，并考察不同的下限截止频率取值，其表示为第1响应主频f1的不同比例。最后分别与精确参考解进行对比，并采用如下定义的总体误差指标来评价积分精度

(18)

3.1 多频简谐激励情况

在多频简谐激励下，以质点3处的竖向响应为例，图5给出了不同噪声水平下两种方法的结果精度对比，图6～图8分别给出了25%噪声水平下两种方法滤噪后的加速度频谱对比，积分所得的位移时程对比，以及取不同下限截止频率时的频率截止法的计算精度。

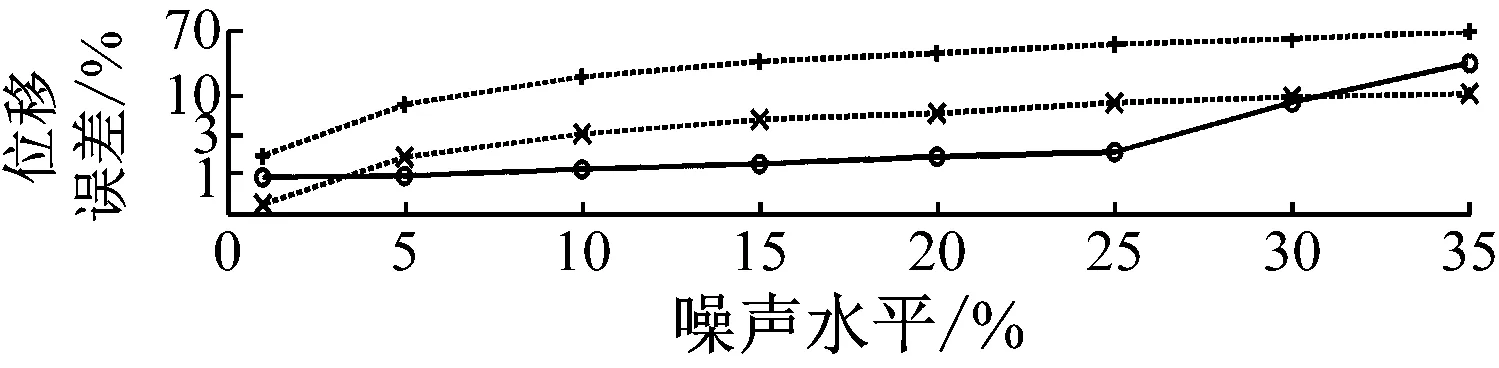
图5 不同噪声水平下的结果误差

由图5～图8可知，在简谐激励作用下，

(1) 频率截止法的计算精度，尤其是对于积分位移响应，受下限截止频率的影响非常大，积分精度与截止频率间满足单调关系；同时，随着噪声加大，计算精度变差；

(2) 有效频段法计算得到的三种响应，在绝大部分情况下均较频率截止法的结果精度更高；在25%噪声水平以下时，结果误差均为1%～2%，即使在25%噪声干扰下，积分位移也几乎与精确位移重合。

图6 25%噪声下的滤噪后加速度频谱

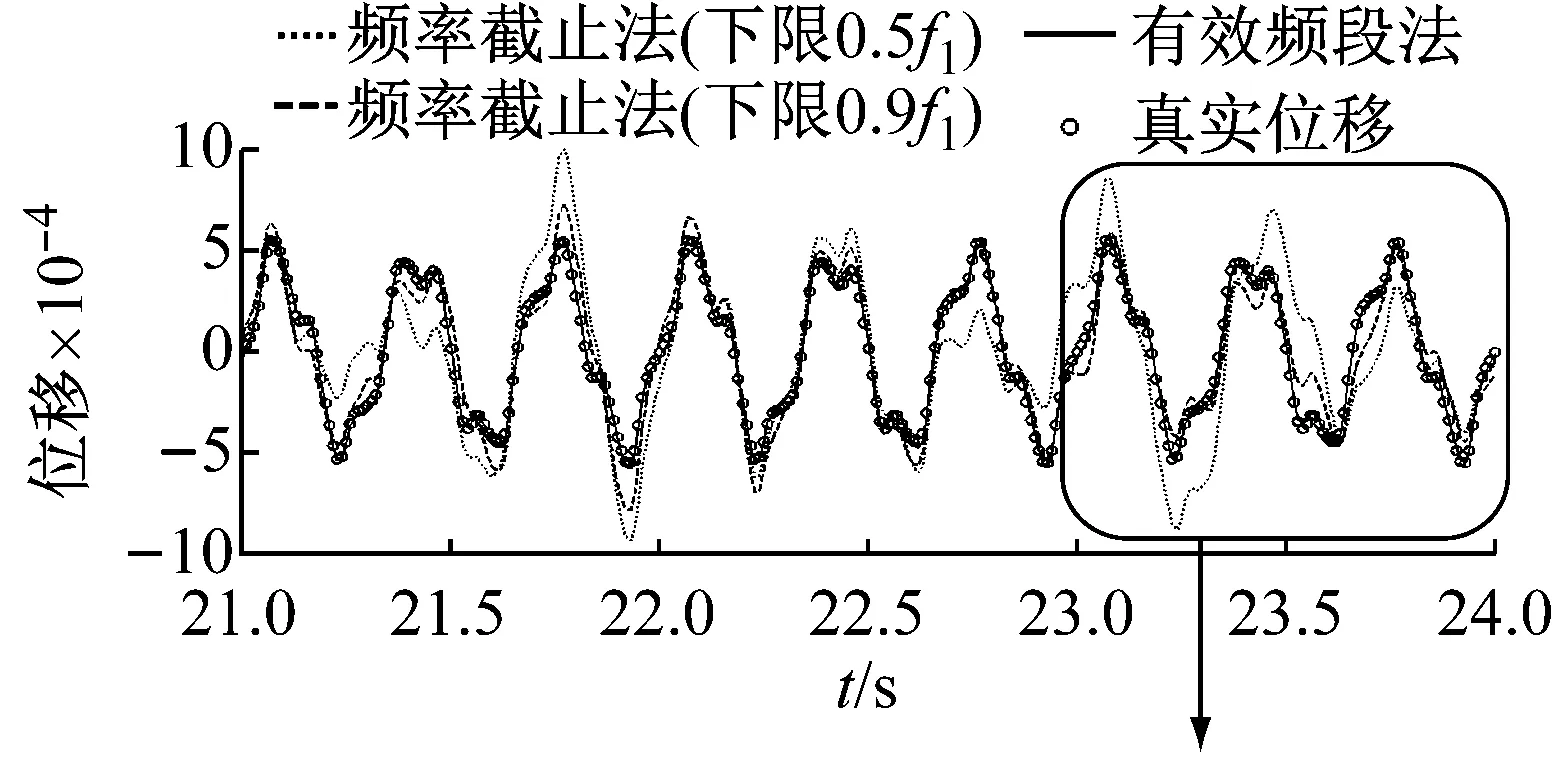
图7 25%噪声下的位移时程

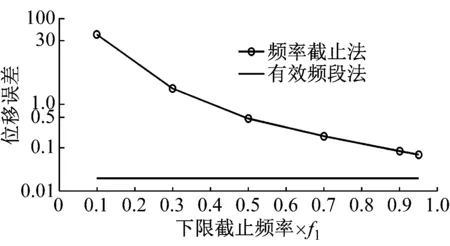
图8 25%噪声下取不同下限截止频率时的位移误差

3.2 随机激励情况

在随机激励下，同样以质点3处的竖向响应为例，图9给出了不同噪声水平下两种方法的结果精度对比，图10～图12分别给出了25%噪声水平下两种方法滤噪后的加速度频谱对比，积分所得的位移时程对比，以及取不同下限截止频率时的频率截止法的计算精度。

由图9～图12可见，在随机激励作用下，

(1) 频率截止法的计算精度，尤其是对于积分位移响应，受下限截止频率的影响同样非常大，但积分精度与截止频率间不完全满足单调关系；同时，随着噪声加大，计算精度同样容易变差；

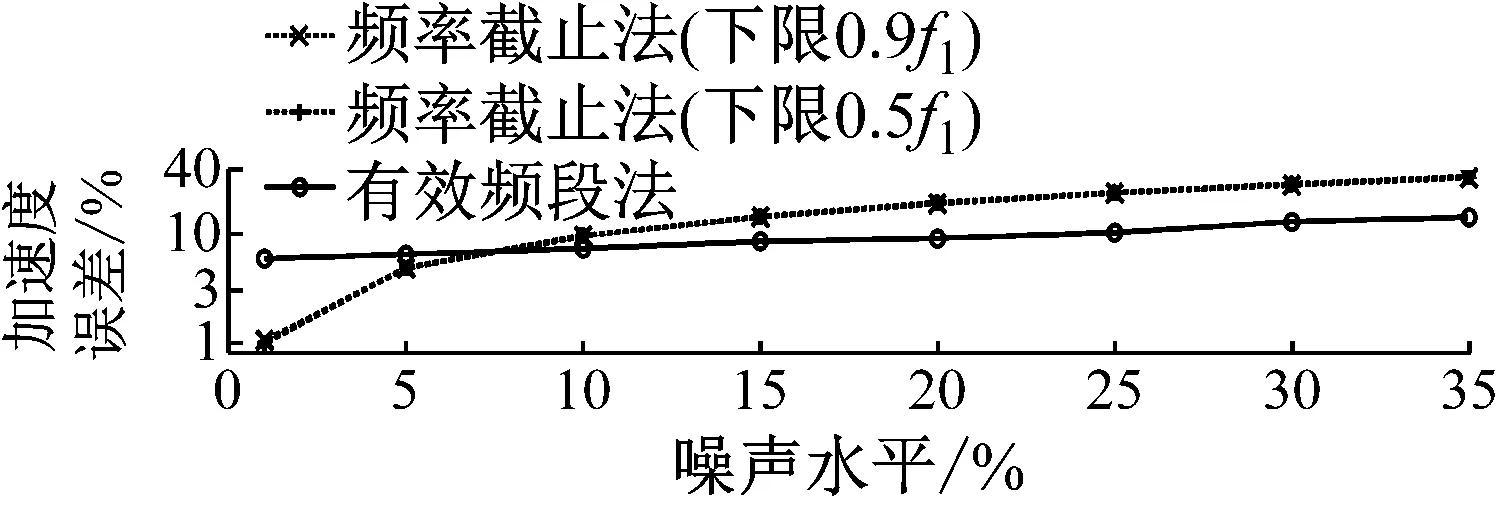
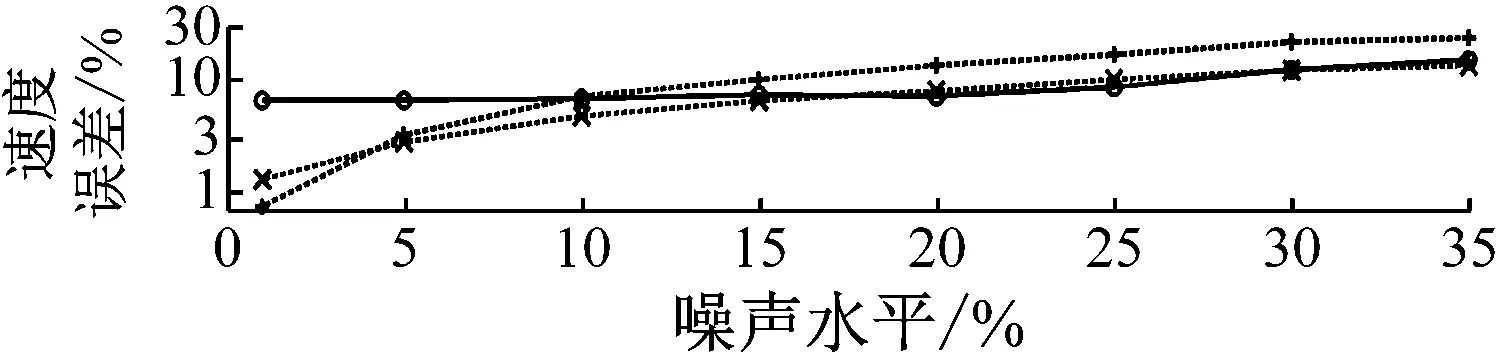
图9 不同噪声水平下的结果误差

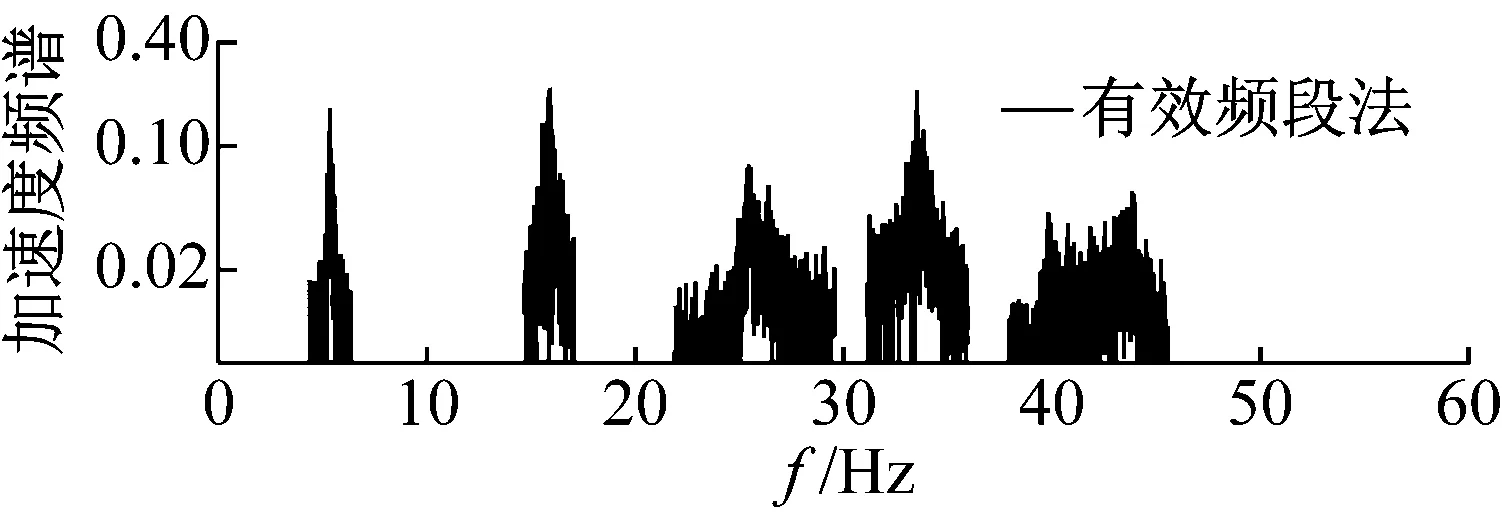
图10 25%噪声下的滤噪后加速度频谱

图11 25%噪声下的位移时程

图12 25%噪声下取不同下限截止频率时的位移误差

(2) 有效频段法计算得到的三种响应，在多数情况下较频率截止法的结果精度更高或相当；在25%噪声水平以下时，结果受噪声水平的影响小，误差在5%～10%间缓慢变化，即使在25%噪声干扰下，积分位移也非常接近于精确位移。

由图5和图9可知，在大于25%噪声水平的情况下，有效频段法的积分精度会随着噪声加大而迅速变差。其原因不仅在于主频处的频谱混入了较大噪声，噪声能量还造成了拟合高斯函数的半径变大，导致积分频率范围扩大，从而引入了更多的主频外的噪声影响。因此，为了保证积分结果的可靠性，建议有效频段法在小于30%的噪声水平下使用。

4 结 论

针对工程振动测试实践中带噪加速度信号的积分问题，常用的频域积分方法如频率截止法等虽然物理意义明确，操作简单直接，相关参数少，但也存在参数敏感、截止频率不易确定等不足。

本文提出有效频段法以改进常规频域积分方法，应用区域频谱形态的高斯函数假定，根据频谱累积能量曲线拟合函数参数，进而自动提取主要积分频段信息，滤除次要频段及其上的噪声影响，有效避免了参数敏感性问题，并提高了积分精度和抗噪性。在应用有效频段法时，虽然需要知道响应的主频信息作为输入参数，但该信息仅用于频域初步分段，而非最终的积分频段，因此仅需已知主频的近似取值即可，而这些信息通常可以通过频谱分析容易获得。这一较低的参数要求特点也有助于有效频段法在工程实践中方便应用。

还需说明的是，由于应用了傅里叶变换，因此有效频段法与频率截止法类似，均仅适用于稳态加速度信号的积分处理，包括简谐激励和平稳随机激励的实际情况。针对非稳态加速度信号的积分处理的相关研究，仍在进行中，后续将另文报告有关结果。