郭晨，肖志芳，冷明，彭硕，王博

（1. 井冈山大学电子与信息工程学院，江西 吉安 343009；2. 江西省农作物生长物联网技术工程实验室，江西 吉安 343009）

1 引言

随着电子工业的飞速发展，计算机系统中处理器的规模越来越大，尺寸越来越小。而在处理器规模不断扩大的同时，计算机系统的故障风险也变得越来越高，由此引发了一系列可靠性问题的研究，其中又以故障的诊断问题最为迫切[1]。传统的故障诊断是通过一个所谓的“中心处理器”来测试每一个处理器的运行状态，从而给出故障评价，这种诊断方式工作量巨大并且多数情况都需要断电甚至拆解系统，既不精确也缺乏可行性。因此，1967年，Preparata等[2]提出了一种基于图论的系统级故障诊断（system level diagnosis）理论。系统级故障诊断充分利用了每一个处理器的处理能力，让处理器之间进行相互测试，通过综合分析来识别故障。通常情况下系统级故障诊断可以带电进行。因此，系统级故障诊断既经济又便捷，是多处理器并行计算机故障诊断的主要发展方向之一。

系统级故障诊断的执行还依赖特定的诊断策略(diagnostic strategy)。1967年，Preparata等[2]首次将图论方法运用于多处理器并行计算机系统的故障诊断，创造性地提出了t-可诊断策略。t-可诊断表示当系统的故障处理器数不超过t时，所有故障都可以被诊断出来。t-可诊断又可以根据迭代次数的不同，进一步分为一步t-可诊断和顺序t-可诊断这2种类型。其中，一步t-可诊断只需要一次迭代即可完成，而顺序t-可诊断则需要反复迭代，直到所有故障都被确认为止，每一次迭代都需要有新的故障被确认。顺序t-可诊断是一种通过多步诊断来有效提高系统诊断能力的诊断方式，与一步t-可诊断相比，顺序t-可诊断在诊断能力相同的情况下，可以较大程度地节省测试成本。

根据顺序t-可诊断的定义可知，在最坏情况下，顺序t-可诊断的每一次迭代只能确定一个故障节点，因此整体的迭代过程可能需要很长的时间，这大大降低了诊断的实时性。基于此，2003年，Araki等[3]提出了新一代的顺序t-可诊断理论——(t,k)-可诊断。(t,k)-可诊断要求系统在故障节点数不超过t时，每次迭代至少可以确定k个故障节点。(t,k)-可诊断最坏情况下的最大迭代次数仅为比顺序t-可诊断的最大迭代次数t要小很多。因此，(t,k)-可诊断改善了顺序t-可诊断的过度时延，是顺序故障诊断的发展方向。事实上很多故障诊断理论都存在故障随机分布和故障条件分布这 2种情景[4]，(t,k)-可诊断也不例外。在故障随机分布的情况下，k=t时的(t,k)-可诊断就是一步t-可诊断，k=1时的(t,k)-可诊断就是顺序t-可诊断。而对于故障节点不是随机分布，而是和条件t-可诊断[1]一样。要求所有的节点都至少有一个正确的邻节点的情况，2011年，Chang等[4]把这种情况下的(t,k)-可诊断定义为条件(t,k)-可诊断。条件(t,k)-可诊断充分融合了条件t-可诊断和(t,k)-可诊断的优点，在有效利用测试资源的基础上提高了系统的诊断能力。因此，(t,k)-可诊断和条件(t,k)-可诊断成为了当下的研究热点[5-11]。其中，Chang等[5]通过研究得出Preparata等[2]提出的PMC模型下超立方网络(Qn)、扭立方网络(TQn)、交叉立方网络(CQn)和莫比乌斯立方网络(MQn)的(t,k)诊断度均为。Chen等[6]在此基础上进一步证得MM模型下Qn、TQn、CQn和MQn的(t,k)诊断度为，并进一步给出PMC模型下针对超立方网络等分支组合图(component-composition graph)(t,k)诊断度的通用求法[9]。2016-2017年，文献[10-11]则分别给出了PMC模型下交换超立方网络(EH(s,t))和MM模型下扩展立方体网络(AQn)的(t,k)诊断度。(t,k)-可诊断改善了顺序t-可诊断的过度时延，是顺序故障诊断的发展方向。

互连网络(interconnection network)是一个专门服务于处理器和内存模块的通信机制[12]。迄今为止，互连网络已发展成一个以超立方网络及其变种为代表的具有多重继承关系的拓扑结构集族。交换交叉立方网络(ECQ, exchanged crossed cube)[13]是新型互连网络的最新研究成果，它同时集成了交换立方网络[14]和交叉立方网络[15]的优点，是多处理器并行计算机系统的一种更加优化的组织形式。然而迄今为止，交换交叉立方网络中以各种诊断度为代表的可靠性研究，如诊断度、g-正确邻节点条件诊断度[16]、(t,k)-诊断度等均未有结果，这就严重制约了交换交叉立方网络的应用和推广。

基于此，本文以交换交叉立方网络为研究对象，首先对其拓扑性质展开研究，在得到交换交叉立方网络相关拓扑性质的基础上，对交换交叉立方网络在 PMC模型下的(t,k)-诊断度进行研究，通过理论推导得到了交换交叉立方网络ECQ(s,t)在PMC模型下满足(s+1,s+1)-可诊断和可诊断，其中0≤δ＜1，1≤s≤t。进而通过仿真验证了结论的正确性。本文的研究进一步分析了交换交叉立方网络的可靠性能，为交换交叉立方网络的应用和推广扫清了障碍，具有较强的理论价值和现实意义。

2 预备知识

2.1 PMC模型

迄今为止，系统级故障诊断已经提出了多种故障诊断模型，但是使用最为广泛的还是 1967年Preparata等[2]提出的PMC模型。在PMC模型中，系统用有向图G(V,E)表示，其中，V表示处理器节点集合，E表示测试边集合。G(V,E)中任意的节点u表示为u∈V，如果存在着节点u测试节点v，则表示为(u,v)∈E。测试的结果用σ(u,v)表示，当节点u对节点v的测试评价是正确时，表示为σ(u,v)=0；否则表示为σ(u,v)= 1。系统所有的测试结果统称为系统的一个症候，用σ表示。PMC模型认为当测试节点无故障时测试结果真实可信，而当测试节点本身是故障节点时测试结果不可信。PMC模型下的测试规则如表1所示，其中，u、v表示任意2个节点；u=0表示u是正确节点，u=1表示u是故障节点；σ(u,v)表示节点u对节点v的测试结果。

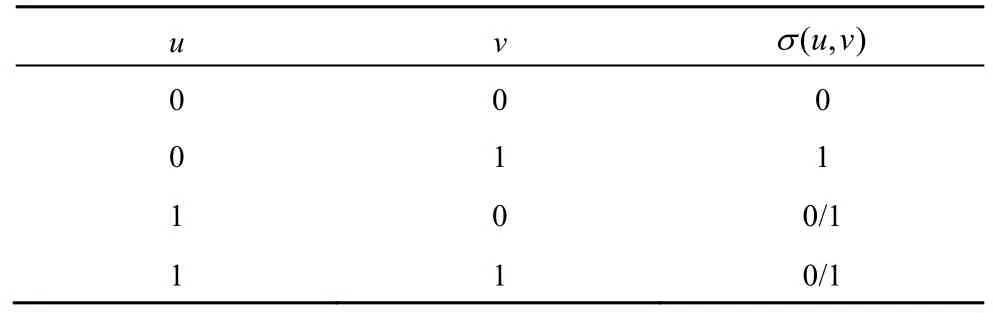
表1 PMC模型的测试规则

2.2 交换交叉立方网络

交换交叉立方网络是 Li等[13]提出的一种新型互连网络拓扑结构，它同时继承了交换超立方网络和交叉立方网络的拓扑性质，表现出更高的性价比。

交换交叉立方网络的定义需要首先引入关联对的概念。

定义1[15]设2个长度为2的二进制字符串X和Y，其中X=x1x0，Y=y1y0。X～Y表示X和Y是关联对，当且仅当(X,Y)∈{(00,00),(10,10),(01,11),(11,01)}时，X～Y。

定义2[13]交换交叉立方网络表示为ECQ(s,t)，其中，s≥1，t≥1。通常用图G(V,E)进行定义，其中，节点集合i∈[0,s),j∈[0,t)}。V中任意节点用一个“s+t+1”位的二进制字符串表示，u[i]表示节点u在位置i的取值用，u[i:j]表示节点u从第i个位置到第j个位置的取值用，其中i≤j。边集合E包括3种类型，分别表示为E1、E2和E3，其定义如下。

E1：u[0]≠v[0]，且u[(s+t):1]=v[(s+t):1]时的边(u,v)∈E1。

E2：u[0]=v[0]=0，且u[t:1]=v[t:1]，存在着正整数l，(s+t)≥l＞t，有u[(s+t):l]=v[(s+t):l]，如果l-t是偶数，那么D={1as-2…a0bt-1…b01|ai,bj∈{0,1}forj∈[0,s-2],i∈[0,t-1]}，u[t+2i+2:t+2i+1]～v[t+2i+2:t+2i+1]，其中E2，那么边(u,v)∈E2；

E3：u[0]=v[0]=1，且u[(s+t):(Δt+1)]=v[(s+t):(t+1)]，存在着一个正整数l，t≥l≥1，有u[t:l]=v[t:l]，u[l-1]≠v[l-1]。如果(l-1)是偶数，那么u[l-2]=v[l-2]。u[(2i+2):(2i+1)]～v[(2i+2):(2i+1)]，其中，那么边(u,v)∈E。3

由 ECQ(s,t)的定义可知，其中，属于E1的边2s+t条，属于E2的边2s+t-1t条，属于E3的边2s+t-1s条。

ECQ(1,1)、ECQ(1,2)和ECQ(2,2)的拓扑结构如图1～图3所示，其中虚线、粗实线和细实线分别表示E1、E2和E3。

图1 ECQ(1,1)拓扑结构

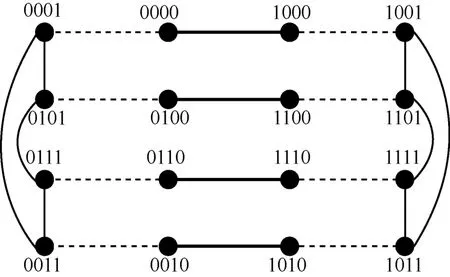
图2 ECQ(1,2)拓扑结构

图3 ECQ(2,2)拓扑结构

ECQ(s,t)具有以下性质。

引理1[13]ECQ(s,t)的所有节点中，c位置取值为0的节点的度为s+1，c位置取值为1的节点的度为t+1。

因此可知，1≤s≤t时 ECQ(s,t)的最小度

引理 2[13]ECQ(s,t)可以划分成 2个ECQ(s-1,t)或者2个ECQ(s,t-1)。

由引理 2可以把 ECQ(s,t)划分为 2个ECQ(s-1,t)，分别表示为L和R，其中，L的节点集，R的节点集V(R)=。进一步把V(L)分为A和B这2个节点集合，把V(R)分为C和D这 2个节点集合，A、B、C和D的定义如下[13]

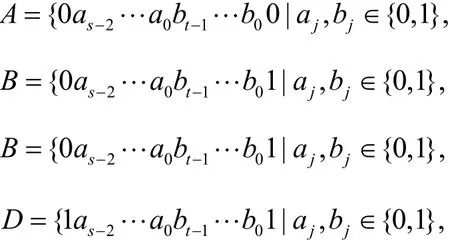
由A、B、C和D的定义可知，2个端点都属于A的边是E2边，2个端点都属于B的边是E3边，2个端点都属于C的边是E2边，2个端点都属于D的边是E3边，2个端点分别属于A和B的边是E1边，2个端点分别属于A和C的边是E2边，2个端点分别属于C和D的边是E1边。同时A∪B、A∪C和C∪D都是完美匹配[17]，如图4所示。

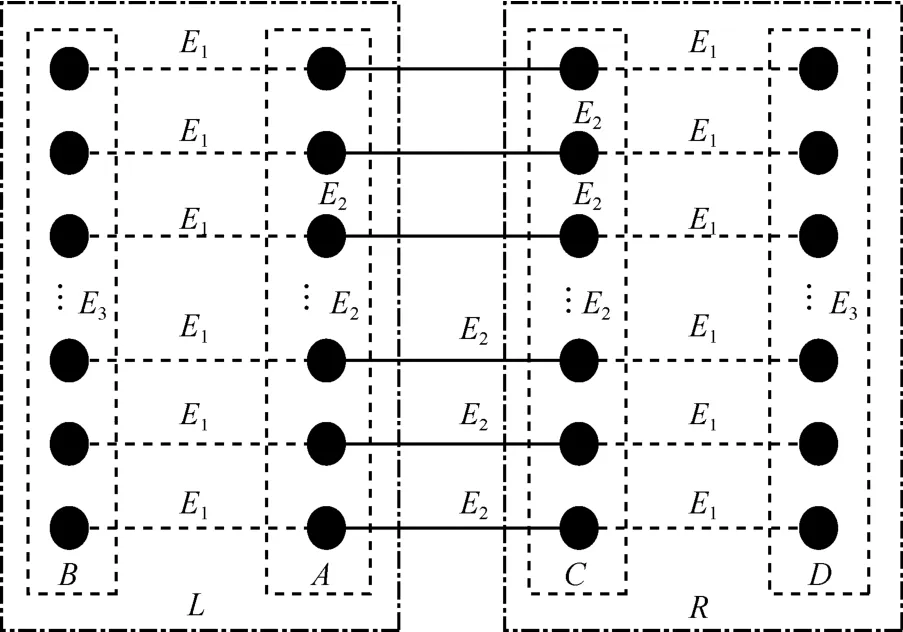
图4 节点集合A、B、C、D示意

引理3[13]ECQ(s,t)与ECQ(t,s)同构，表示为

引理 4[17]ECQ(s,t)的点连通度k(ECQ(s,t))=s+1，其中1≤s≤t。

引理 5[18]ECQ(s,t)的拓扑结构不含节点三角（triangle-free）。

由引理5可知，对于ECQ(s,t)中任意的2个节点u和v，如果(u,v)∈E(ECQ(s,t))，那么|N(u)∩N(v)|=0，其中，N(u)和N(v)分别表示节点u和节点v的邻节点集合。

2.3 (t,k)-可诊断

(t,k)-可诊断是2003年Araki和Shibata[3]共同提出的新一代顺序t-可诊断，(t,k)-可诊断要求在故障节点不超过t个的情况下，迭代进行故障诊断，每一次迭代至少可以识别出其中的k个故障节点，其中k≤t。具体定义如下。

定义3[3]对于2个正整数t和k，k≤t，设F是系统的故障节点集合，给定症候下当系统满足以下2个条件时系统是(t,k)-可诊断系统。

1) 当|F|≤k时，所有的故障节点都可以被诊断出来。

2) 当k＜|F|≤t时，至少有k个故障节点可以被诊断出来。

给定一个正整数k≥1，系统满足(t,k)-可诊断时，t可取到的最大正整数称为系统的(t,k)-诊断度。当系统是(t,k)-可诊断系统时必然也是(t,k′)-可诊断系统，其中1≤k′＜k。(t,k)-可诊断可通过引理6进行判定。

引理 6[3]系统是(t,k)-可诊断系统，当且仅当对于任意故障节点数不超过t的症候σ，或者其中，是与症候σ一致的故障节点集合，并且|F|≤t}。

根据定义3可知，当k=t时，(t,k)-可诊断就是一步t-可诊断，因此，k=t时的(t,k)-诊断度可以按照一步t-可诊断的诊断度来求取，如引理7所示。

引理 7[19]设系统S有n个节点，如果S的点连通度k(S)≥t并且n≥(2t+1)，那么系统S是一步t-可诊断系统。

为了区分开(t,k)-可诊断和交换交叉立方网络ECQ(s,t)中的t，下文将把(t,k)-可诊断改写成(t1,k)-可诊断，其定义和性质定理维持不变。

2.4 集团

集团是 1998年张大方等[20]提出了一种特殊的连通分支，集团内的节点具有状态相同的特点。具体定义如下。

定义 4[20]系统G(V,E)中满足以下 2个条件的连通分支H，则称为集团。

1)H中任意相邻的 2个节点之间的测试结果都为“0”。

2)H中任意的节点如果与H以外的节点相连接，那么它们之间的互测结果不能同时为“0”。

在给定症候的情况下，可以通过断开所有测试结果为“1”的互测边，求取强连通分支的方式来得出所有的集团。以ECQ(1,2)为例，它的症候如图5所示，那么断开所有测试结果为“1”的互测边之后如图6所示。因此，该系统的集团有6个，分别是{0001,0000,0101}、{0100,1100}、{0111}、{1000,1001, 1101}、{0110,1110,1111}和{0011, 0010, 1010,1011}。

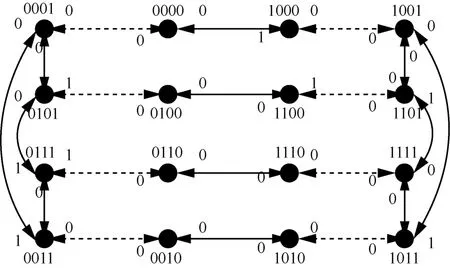
图5 ECQ(1,2)的给定症候示意

集团具有以下性质，如引理8～引理10所示。

引理8[20]集团中所有节点要么全都是故障节点，要么全都是正确节点。

图6 图5中包含的集团示意

通常情况下把全部是正确节点的集团称为正确集团，把全部是故障节点的集团称为故障集团。

引理9[21]如果系统的故障节点数不超过t，那么系统中节点数大于t的集团必定是正确集团。

引理10[21]正确集团只能和故障集团相邻。

G(V,E)在给定症候下的所有集团归为集合V+，不同集团之间的邻接集合E+，表示为E+={(X,Y)|X∈V+,Y∈V+,(x,y)∈E,x∈X,y∈Y}。由此可以把G(V,E)表示为G+(V+,E+)。集团集合V+的独立子集V+′，指的是V+′⊂V+并且V+′中的任意集团之间都不相邻。

定义5[5]ϕ(x1)表示m可取到的最小正整数。指的是在G+(V+,E+)中，V+存在着一个满足的子集V+′，是V+的独立子集，使得V+-V+′中不存在满足|Xi|≥x1的集团Xi。

定义6[5]φ(x1,x2)表示p可取到的最大正整数。指的是在G+(V+,E+)中，对于V+中满足|V+′|≤p的每一个子集V+′，V+-V+′是V+的独立子集，则至少存在着一个属于V+-V+′的集团Xi，Xi满足以下2个条件。

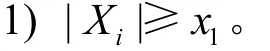
定义7[5]函数I(m)表示节点数为m的所有节点子集中，2个端点都属于该子集的边的最大数目。

由I(m)的定义可知，I(1)=0。

3 交换交叉立方网络的拓扑性质

接下来，对交换交叉立方网络拓扑结构的邻节点性质展开研究。

定理1设节点u和节点v是ECQ(s,t)中任意的2个节点，则N(u)∩N(v)≤2。

证明用数学归纳法证明。由图 1～图 3可知，ECQ(1,1)、ECQ(1,2)和ECQ(2,2)都满足N(u)∩N(v)≤2。假设ECQ(s-1,t)(或者ECQ(s,t-1))也满足N(u)∩N(v)≤2。接下来证明ECQ(s,t)是否满足N(u)∩N(v)≤2。根据引理 2把ECQ(s,t)划分为2个ECQ(s-1,t) (或者ECQ(s,t-1))，分别表示为L和R。不失一般性，设当u,v∈V(L)(或者u,v∈V(R))时，N(u)∩N(v)⊂V(L)(或者N(u)∩N(v)⊂V(R))。根据数学归纳法的假设可知|N(u)∩N(v)|≤2。而当u∈V(L)并且v∈V(R)(或者u∈V(R)并且v∈V(L))时，如图4所示，由于A和C之间是完美匹配，所以|N(u)∩N(v)|≤2。因此，定理1可证，证毕。

定理2设节点u和节点v是ECQ(s,t)中任意的2个节点，且(u,v)∈E(ECQ(s,t))，那么

证明由引理 1可知，ECQ(s,t)的所有节点中，c位置取值为 0的节点的度为(s+1)，c位置取值为1的节点的度为(t+1)。所以由引理5可知，当u和v在c位置的取值都为0时，；当u和v在c位置的取值都为1时，；当u和v有一个在c位置的取值为 0，另一个在c位置的取值为 1时，。因此证毕。

在得到 ECQ(s,t)相关拓扑性质的基础上，对 ECQ(s,t)在 PMC模型下的(t1,k)-诊断度展开研究。

4 交换交叉立方网络在PMC模型下的(t1,k)-可诊断

首先进行函数ϕ(x1)、φ(x1,x2)和I(m)的取值研究。

定理3在ECQ(s,t)中，

证明根据引理 2可把ECQ(s,t)划分为 2个ECQ(s-1,t)，分别表示为L和R，其中，V(L)=如图4可知，节点集合A中的每一个节点都与节点集合C中的一个节点相邻接。对于ECQ(s,t)的任意节点子集X和Y，设由于YL中的任意节点至多只有一个属于YR的邻节点，反之也一样，因此存在着如式(1)所示的不等式。

Y内部的边数≤LY内部的边数+

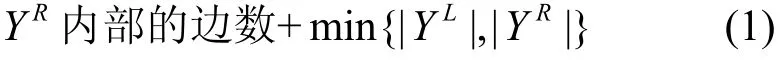
设IL(m)(或者IR(m))表示属于L(或者R)且节点数为m的节点子集包含内部边的最大数目，同样有IL(1)=0、IR(1)=0。由不等式(1)可知，I(|Y|)≤。不失一般性地，设则那么，

接下来，用数学归纳进行证明。由图1～图3可知，ECQ(1,1)、ECQ(1,2)和ECQ(2,2)都满足。假设ECQ(p,q)也有其中1＜p＜s、1＜q≤t。那么接下来证明ECQ(s,t)是否满足

当β=0时由归纳法的假设可知因此。当β≥1时，，同样由归纳法的假设可知设函数，可知f′(β)=由于，可知β=1或者时f()β可取到最大值。由于所以I(m)≤mlbm，定理3可证，证毕。

接下来，对ECQ(s,t)在PMC模型下满足(t1,k)-可诊断时k和t1的取值进行研究。

4.1 k的取值研究

给定症候下的ECQ(s,t)用表示，其中1≤s≤t。设集团XV+∈，VX表示X的节点集合，VN(X)表示X的邻节点集合。由ECQ(s,t)和集团的定义可知|X|＞0、|VN(X)|＞0，并且X具有以下性质。

定理4把G(V,E)表示为G+(V+,E+)，设集团X∈V+，则|VN(X)|≥k(G)或者

证明由X和VN(X)的定义可知，X和V-VN(X)之间不存在边连接，如果V-VX-VN(X)≠∅则VN(X)是G(V,E)的一个点割集，因此|VN(X)|≥k(G)。而当V-VX-VN(X)=∅时，可以直接推导出V=VX+VN(X)，证毕。

另外可知，从VN(X)发出的到VN(X)以外的边数+VN(X)内部的边数≥VN(X)到VX的边数+VN(X)到V-VX-VN(X)的边数，如图7所示。由引理1可知，ECQ(s,t)中每一个节点的度∈{s+1,t+1}。由于1≤s≤t，所以从VN(X)发出的到VN(X)以外的边数+VN(X)内部的边数≤|VN(X)|(t+1)。VN(X)到VX的边数=VX到VN(X)的边数=VX发出的到VX以外的所有边数－VX内部的边数，因此VN(X)到VX的边数≥|VX|(s+1)-I(|VX|)。同理，由于V-VX-VN(X)与VX之间不存在着边连接，所以VN(X)到V-VX-VN(X)的边数。因此VX-VN(X)|)。由定理3可知所以可得

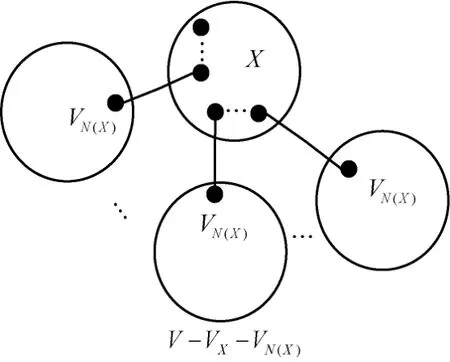
图7 G+(V+,E+)中集团X和VN(X)示意

由不等式(2)可进一步推导出定理5。

定理5在给定症候下，ECQ(s,t)用G+(V+,E+)表示，其中，1≤s≤t。那么对于V+中的任意集团X，都有|VN(X)|≥s+1。

证明由于以下分2种情况进行证明。

情况1|VX|≥2(s+1)并且|V-VX-VN(X)|≥2(s+1)，由于|V-VX-VN(X)|=|V|-|VX|-|VN(X)|，所以可推导出2(s+1)≤|VX|≤|V|-|VN(X)|-2(s+1)＜|V|-2(s+1)。因此，可知4(s+1)＜|V|。设p=|VN(X)|，q=|VX|，所以2(s+1)≤q≤|V|-p-2(s+1)＜|V|-2(s+1)。可以把不等式(2)转换为

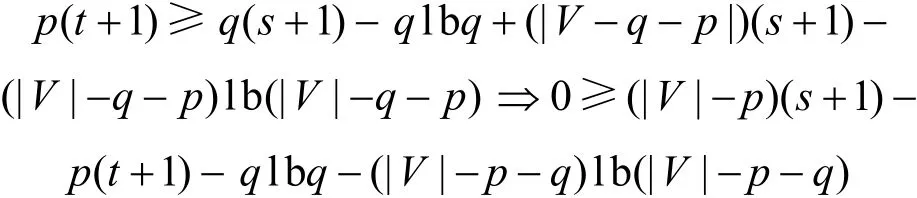
对函数h(p,q)求偏导，可得

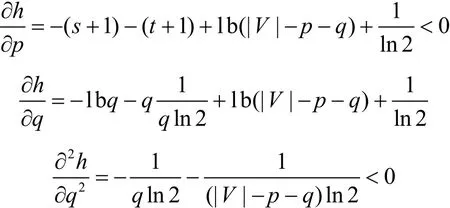
所以h(p,q)是关于变量p单调递减，并且由h(p,q)的一阶偏导和二阶偏导可知，h(p,q)在p取最大值并且q取最大值(或者取最小值)时可以取到最小值。

假设p≤s+1，那么当p=s+1并且q=2(s+1)(或者q=|V|-2(s+1))时h(p,q)可取到最小值。因此，h(s+1,2(s+1))≤h(p,q)，h(s+1,|V|-2(s+1))≤h(p,q)。由于h(s+1,2(s+1))＞0、h(s+1,|V|-2(s+1))≥0，所以要求h(p,q)＞0，这与h(p,q)≤0相矛盾。因此

情况2

情况2.1

情况2.1.1

情况2.1.2

由V≠VX+VN(X)，可知V-VX-VN(X)≠∅。由定理 4可知，|VN(X)|≥k(G)。又由引理 4可知k(ECQ(s,t))=s+1，所以|VN(X)|≥s+1。

情况2.2

证毕。

由引理10和定理5可知，对于给定症候下的ECQ(s,t)，如果可以确定集团X是正确集团，那么可知VN(X)都是故障节点，且|VN(X)|≥s+1。因此，在能确定任意一个正确集团的前提下，ECQ(s,t)在PMC模型下满足(t1,k)-可诊断时k≥s+1。

4.2 t1的取值研究

首先研究ECQ(s,t)中函数ϕ(t1+1)的取值，在此基础上研究满足φ(t1+1,0)≥t1时t1可取到的最大值，进而可以确定ECQ(s,t)在 PMC模型下满足(t1,k)-可诊断时t1的取值。

定理6对于ECQ(s,t)，函数ϕ(t1+1)≥其中1≤s≤t。

证明根据ϕ(x1)的定义可知ϕ(t1+1)≥，表示存在着一个满足的集团子集V′+，使V+-V+′是V+的独立子集，并且V+-V+′中的任意集团Yj都满足|Yj|≤t1。设其中X,X,…,X及12a表示V+中所有的集团，

由于V+-V+′是V+的独立子集，所以集团两两不相邻且由引理1可知，ECQ(s,t)中c位置取值为0的节点的度为s+1，c位置取值为1的节点的度为t+1，其中1≤s≤t。因此，，其中，且V+′与V+-V+′之间的边数目不超过（当从V′+发出的所有边的另一个顶点都属于V+-V+′时可取到最大值）。

由于

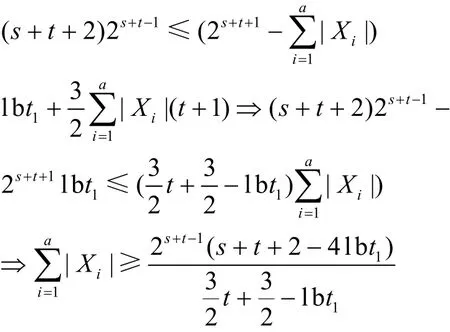
定理6可证，证毕。

基于ϕ(t1+1)和φ(t1+1,0)的关联关系，可通过定理6对φ(t1+1,0)≥t1时t1的取值进行研究，得出定理7。

定理 7对于时函数其中0≤δ＜1。

证明由于所以接下来，需要证明是否成立。设，可以求得。可知当时时h(t1)单调递减。且当时h(t1)＜0，h(t1)的基本走势如图 8所示。 由于时存在着，因此根据的定义可知，时不满足。而当时为了使，则要求同时可知时。因此，其中0≤δ＜1。定理7可证，证毕。

图8 h(t1)的走势

由定理7可知，ECQ(s,t)在PMC模型下满足-可诊断时，如果，其中0≤δ＜1，那么至少存在着一个集团Xi，|Xi|≥t1+1且|N(Xi)|≥0。根据(t1,k)-可诊断的定义可知系统的故障节点数不超过t1时集团Xi必然是正确集团，VN(Xi)是故障节点。

4.3 交换交叉立方网络在 PMC 模型下的(t1,k)-诊断度

由于k=t1时(t1,k)-可诊断就是一步t1-可诊断，ECQ(s,t)在k=t1时的(t1,k)-诊断度如定理 8所示。

定理8ECQ(s,t)满足(s+1,s+1)-可诊断，其中1≤s≤t。

证明由引理4可知，1≤s≤t时k(ECQ(s,t))=s+1。由于1)+1，其中1≤s≤t。由引理7可知，ECQ(s,t)是一步(s+1)-可诊断，因此ECQ(s,t)满足(s+1,s+1)-可诊断，其中1≤s≤t，定理8可证，证毕。

根据定理5和定理7可进一步证得ECQ(s,t)在t1＞k时的(t1,k)-诊断度，如定理9所示。

定理 9ECQ(s,t)满足-可诊断，其中

证明由定理7可知，ECQ(s,t)在PMC模型下满足(t1,k)-可诊断时，如果其中0≤δ＜1，那么至少存在着一个集团Xi，|Xi|≥t1+1且|N(Xi)|≥0。又由定理 5可知，给定症候下ECQ(s,t)的任意集团Xi∈V+，都有|VN(Xi)|≥s+1，其中1≤s≤t。因此，根据(t1,k)-可诊断的定义可知ECQ(s,t)是可诊断系统，其中。证毕。

4.4 仿真实验

接下来，对ECQ(s,t)（1≤s≤t≤5）的(t1,k)-诊断度进行仿真实验验证。仿真算法分为节点编码处理、节点状态编码处理和(t1,k)-诊断度计算3个模块。通过节点编码处理模块和节点状态编码处理模块分别赋给每一个节点一个地址值和一个状态值，其中，地址值用一个长度与维数相等的二进制数表示，状态值用一位二进制表示，如图9所示。

以ECQ(2,2)为例，其拓扑结构如图3所示，共有节点数32个，所有节点的地址值用一个长度为5的二进制表示，通过节点编码处理模块生成的节点地址值如表2所示。

节点有正常和故障2种状态，用“0”表示“正常”状态，用“1”表示故障状态。以ECQ(2,2)为例，通过节点状态编码处理模块之后，32个节点的状态值总共有232种情况，如表3所示。仿真实验并不需要考虑232种的所有的情况，只需要根据t的取值，考虑故障节点数少于等于t个的情况，因此共有Ct32种情况。

(t1,k)-诊断度计算处理模块按照引理 6的充要条件进行设计，包含3个步骤，具体如下。

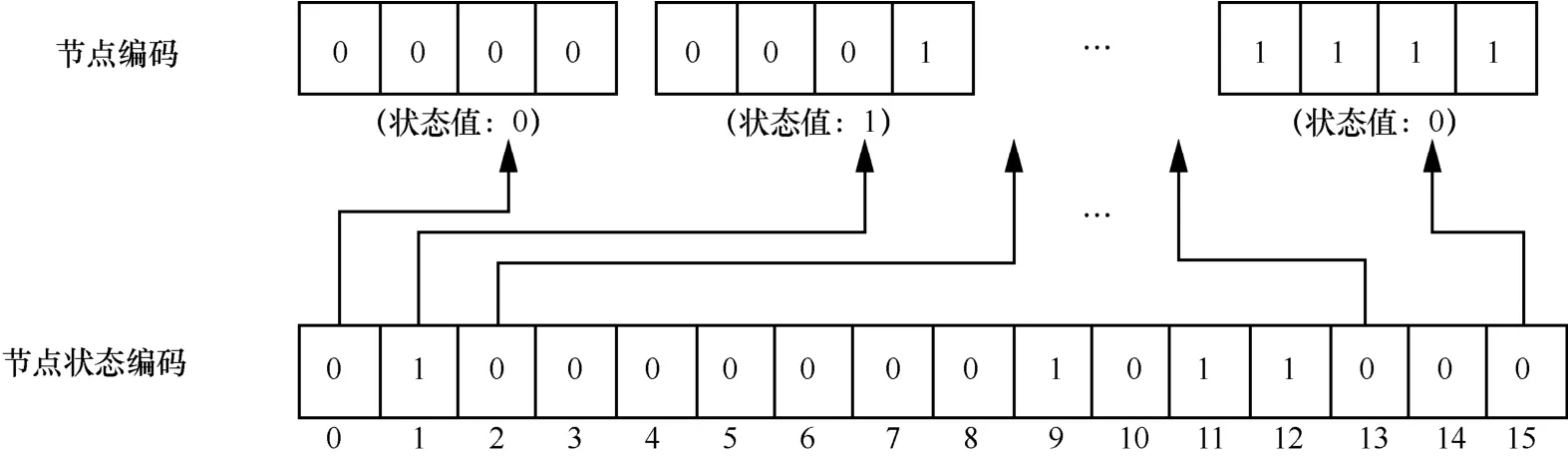
图9 仿真实验的节点编码和节点状态编码

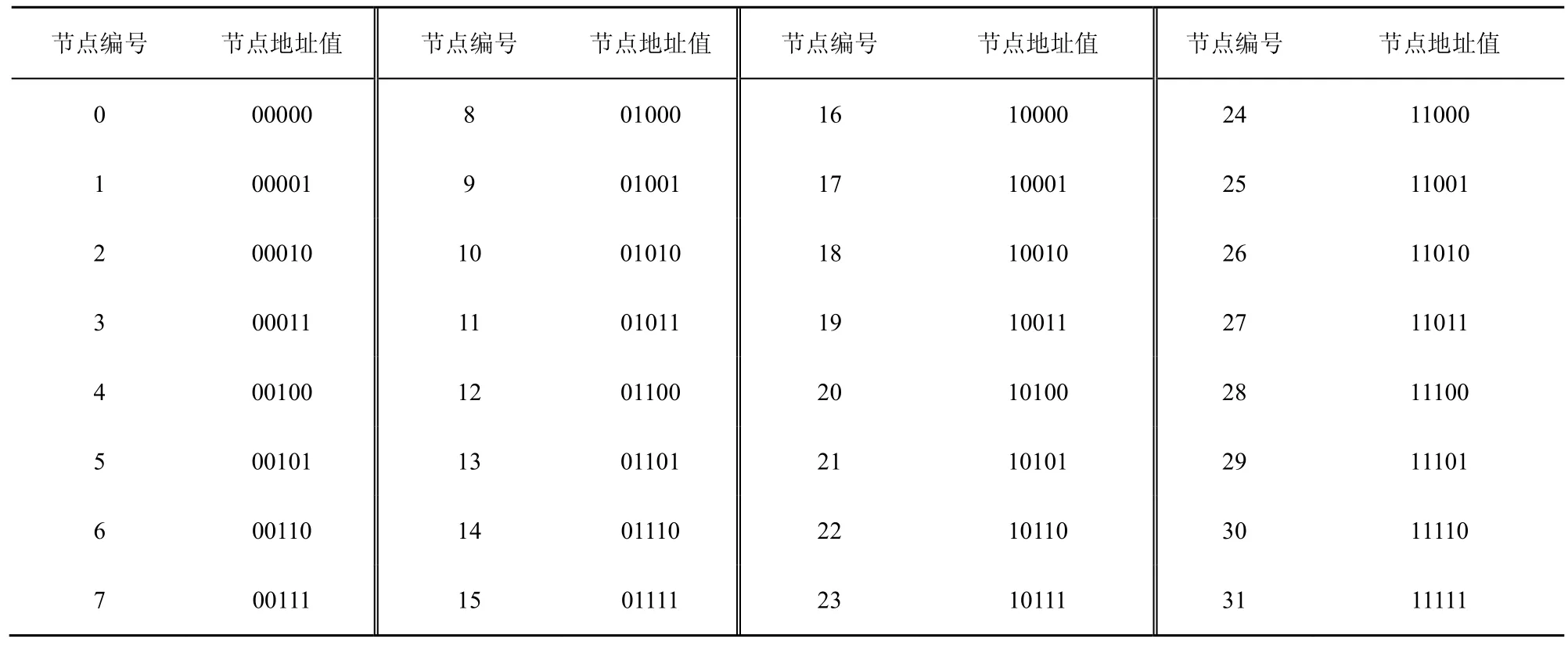
表2 ECQ(2, 2)中32个节点的地址值

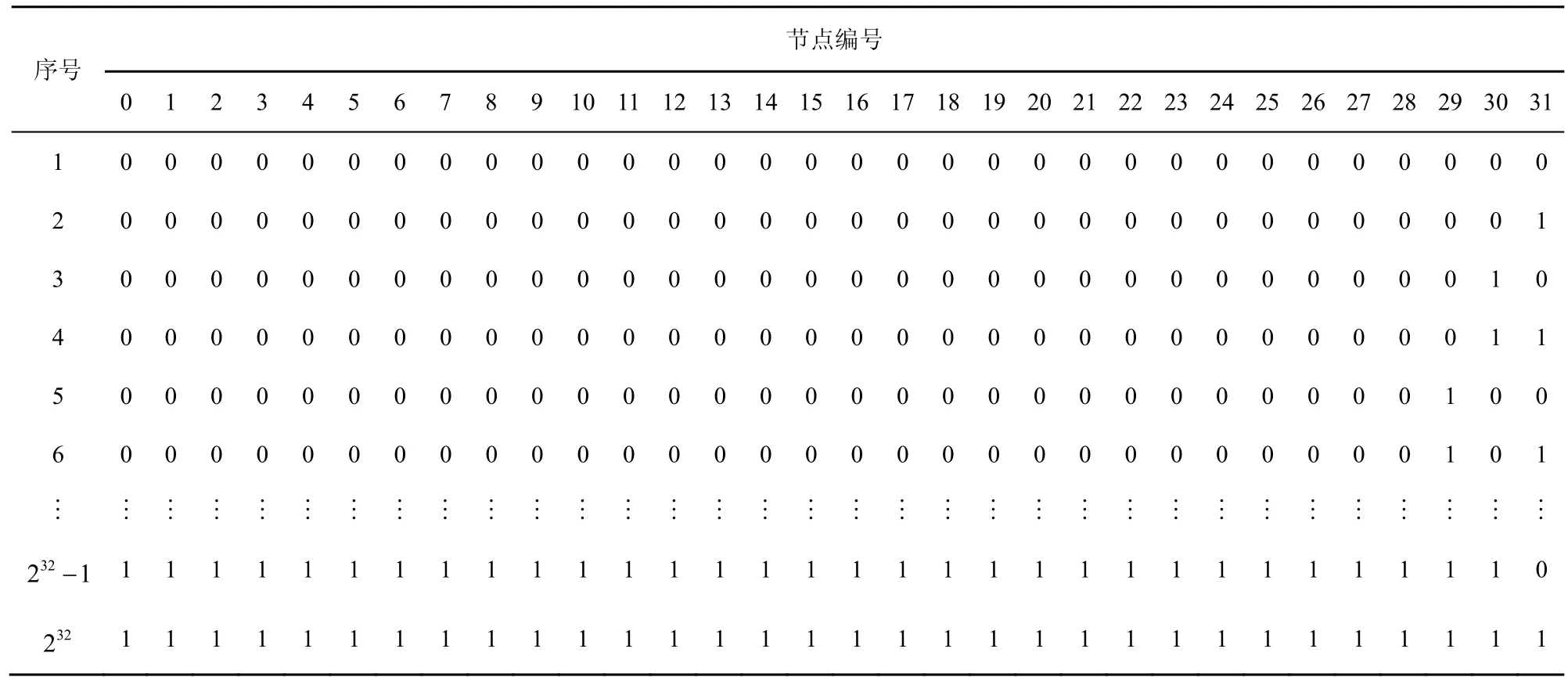
表3 ECQ(2, 2)中32个节点可取的状态值

步骤1计算出ECQ(s,t)中不超过t1个故障节点的所有故障节点集合。

步骤 2对每一种故障节点集合的每一个症候σ，构建出Ωσ,t1。

步骤3如果所有故障节点集合的所有症候都满足或者那么ECQ(s,t)满足(t1,k)-可诊断，否则t1=t1-1，跳转到步骤 1。

以ECQ(2,2)为例，步骤 1中不超过t（t≥1）个故障节点的所有故障节点集合共有（即 35 960）种。设定t=4之后，故障节点集合共有种情况，如表4所示。

进而以第5 178种情况的故障节点集合为例构建起症候，如图10所示。

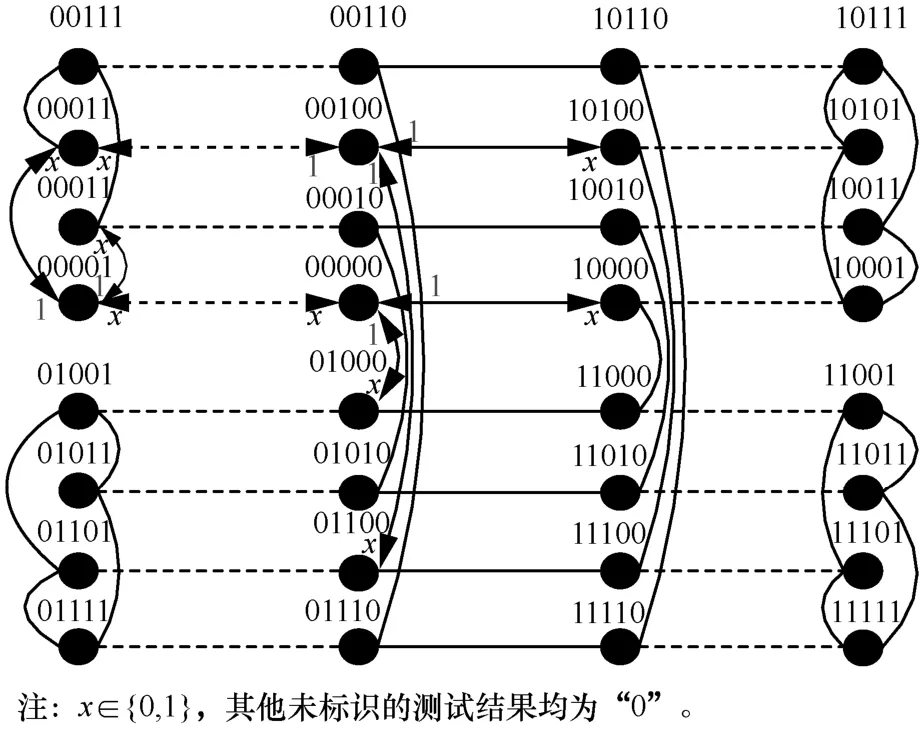
图10 ECQ(2,2)特定症候

与图10症候相一致的故障节点集合，只有表5所示的唯一一种情况。因此，Ωσ,t={00000, 00001,00010}。

节点编码处理模块和节点状态编码处理模块的处理流程相对简单，计算规模较小。仿真实验的主要处理过程集中在(t1,k)-诊断度计算处理模块，通过步骤 1可以取得种故障节点集合，在最坏情况下步骤 2中的每一种故障节点集合最多需要对应2t1个症候，最后通过步骤 3进行循环判断。仿真实验的时间复杂度为O(2nt1)，时间复杂度较高。仿真实验环境为2颗至强E5-4620 v2 CPU，2块16 GB 1 600 MHz内存，2块1.2 TB 10K RPM SAS 6 Gbit/s硬盘，Microsoft SQL Server 2008数据库。通过计算得出的仿真实验数据如表6所示。实验结果进一步印证了定理7和定理8的结论。

实际应用中可以引入环诊断算法[22]进行(t1,k)-故障诊断。根据环诊断算法，对初始症候进行局部识别，借助0→0→…→0→1的局部症候来识别故障节点，进而在替换掉已识别故障节点的基础上进行第二次迭代故障诊断，直到所有的故障节点都被识别为止。

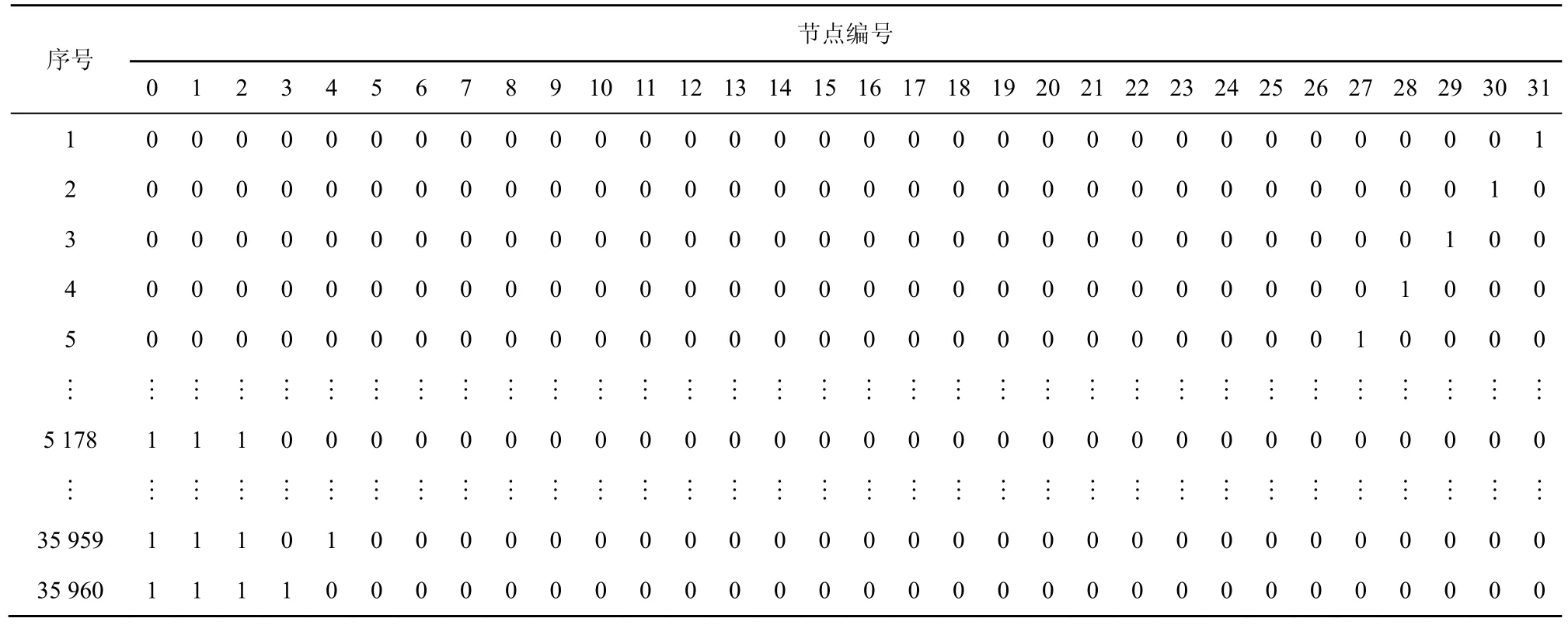
表4 故障节点数不超过4时ECQ(2, 2)的35 960种故障节点集合

表5 与图10症候相一致故障节点集合

5 结束语

本文以ECQ(s,t)为研究对象，首先对ECQ(s,t)的拓扑结构展开研究，证得了ECQ(s,t)在邻节点方面的相关拓扑性质。在此基础上引入集团的思想，借助3个重要函数证明了ECQ(s,t)在PMC模型下是(s+1,s+1)-可诊断和可诊断，其中最后通过仿真实验验证了结论的正确性。本文的研究成果将有利于进一步理清交换交叉立方网络的可靠性，为交换交叉立方网络的应用和推广奠定了坚实的理论基础。

表6 仿真实验数据与理论推导结果