徐利锋, 黄祖胜, 杨中柱, 丁维龙

(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)

粒子群优化算法(particle swarm optimization,简称PSO)是由Kennedy和Eberhart于1995年提出的一种模拟鸟群觅食特性的进化算法[1].在算法中,粒子代表着觅食中的鸟个体.在每个粒子移动时,同时考虑整个群体的最优位置和当前粒子曾经经历过的最优位置,类似于鸟群觅食时鸟之间的信息交流.当群体中所有粒子都移动之后,记为一轮优化迭代完成,接着进行下一轮优化迭代,直到满足预设的迭代深度或者其他条件为止.整个群体就像鸟群觅食一样,总是向着最优位置移动.

PSO算法具有易操作和收敛快等优点,但也存在着一些问题,比如因其收敛快而导致的易陷入局部最优值,以及算法在多局部峰值场景中的精确性不高等问题.研究者们一直在针对 PSO的这些问题进行针对性的研究和改进,并提出一些解决方法,形成了若干PSO的改进算法.其中,Shi和Eberhart于1998年提出的带有惯性权重的粒子群优化算法[2],便是针对最初的PSO算法易陷入局部最优值的改进.Clerc于1999年提出了带压缩因子的粒子群优化算法[3],意在摆脱局部最优值的同时提高收敛速度.这是两种最经典的改进PSO算法,其他的改进算法一般都是在此基础之上通过与其他方法结合或是针对参数进行修改来获得新的改进算法.例如,刘丽珏等人提出了基于克隆选择的粒子群优化算法[4],主要利用了克隆和变异操作来提高算法的收敛速度,并保持种群多样性.再如,针对多目标优化问题而提出的基于网格排序的多目标粒子群优化算法[5]、为逼近非凸或不连续的Pareto最优前端而提出的基于Pareto熵的多目标粒子群优化算法[6]、面向粒子群优化算法中学习因子自调节优化器的PSO算法[7]、基于粒子群优化算法的类集成测试序列确定方法[8]、加入了微生物行为机制的粒子群优化算法[9]以及微分进化算法与粒子群优化的结合[10]和其他一些针对 PSO参数进行自适应选择的算法[11,12]等.这些改进的算法直接针对PSO算法本身存在的缺陷进行弥补.另外,还有一些改进算法实现了在不同领域中的适配和应用.对于算法适配,例如：对典型的NP难题中的Web服务组合优化问题,研究者提出了基于改进粒子群算法的Web服务组合[13];ECT系统中如果忽略电容传感器的敏感场(又叫软场),会使传统图像重建方法精度下降,为了清除这个瓶颈,提出了基于双粒子群协同优化的 ECT图像重建算法[14];为了在不修改源代码的同时能够评价优化目标的每个分支,提出了粒子群优化测试用例生成方法[15].对于算法应用,例如跳跃-滑翔轨迹优化研究(混沌粒子群算法)[16]、电力系统环保经济负荷分配应用研究(空间粒子群优化算法)[17]以及求解服务链映射问题(离散粒子群优化算法)[18]等.

上述各种基于PSO的改进和适配后优化算法各有优点,但总体来说都是尝试去解决原始PSO算法的固有问题——易于陷入局部极值的问题.针对这种问题,本研究基于现有的两种经典改进PSO算法,在不过分提高算法时间复杂度的前提下,通过引入多级扰动策略来避免PSO算法易陷入局部最优值的问题,同时也能运用不同的扰动来处理算法探索能力差或算法提前收敛的情况.研究中,运用了 Sphere,Ackley,Rastrigin,Styblinski-Tang,Duadric和Rosenbrock函数对算法的性能进行了测试,并对不同的PSO相关优化算法结果进行对比验证.本研究提出的改进型 PSO算法巧妙地结合了两种经典的改进粒子群优化算法(带惯性权重和带收缩因子的粒子群优化算法)的特性,使得本算法能够将这两种优化算法的优点实现最大化的发挥.同时,针对易陷入局部最优这个问题,提出了多级扰动机制.总体来说,本算法不仅能够增加粒子对于解空间的探索能力,还能够较好地跳出局部最优值.本文首先在第1节介绍上述两种经典的改进粒子群优化算法.然后,在第2节详细讲述了提出的新的改进型PSO算法,即混合型粒子群优化算法的概念及流程.在第3节中,通过对4个测试函数的结合应用,对混合型粒子群优化算法的可行性及准确性进行对比和验证.最后,对本算法和相关的粒子群优化算法进行讨论,对后续研究进行展望.

1 传统粒子群优化算法

1.1 粒子群优化算法

最初提出的粒子群优化算法在模拟鸟群觅食的过程中,各个粒子的位置信息代表解空间中的一个可能的解,速度信息则代表粒子的更新(移动)动力.初始的粒子群优化算法总是能高效地进行更新,从而体现出收敛快的特点.

假设：所要优化的问题的种群大小为n,解空间维数为m,种群中每个粒子的位置为Xi(i=1,2,…,n),每个粒子的适应度值为f(Xi)(i=1,2,…,n),第k代中第i个粒子的位置为Xik,粒子的速度为Vik,第i个粒子得到的最优适应度值的位置为Pik(i=1,2,…,n),所有粒子中得到最优适应度值的位置为Pgk.公式(1)和公式(2)为粒子群优化算法中对于第k代粒子的速度、位置更新公式：

其中,c1和c2为学习因子,r1和r2为使速度具有随机性的随机数,取值在[0,1]之间.

从公式(1)和公式(2)中可以看出,粒子速度更新公式包含了3部分[19,20]：第1部分为粒子当前速度对于之前速度及方向的继承能力;第2部分为粒子的自我认知部分,用来继承粒子历史属性;第3部分为粒子的社会认知部分,表示为所有粒子之间的信息共享,合作地去探索更好的位置.但是由于此方法易陷入局部最优值,所以针对上述更新公式进行一定修改后,得到了下文所提到的两种主流的改进算法.

1.2 标准粒子群优化算法

标准粒子群优化算法(standard particle swarm optimization,简称SPSO),即带有惯性权重的PSO算法,在继承粒子历史速度时,引入惯性权重参数.目的是在寻优问题中,能够先进行全局搜索,在缩小的搜索范围或经过一段时间的搜索之后,再针对当前局部进行更为细致的搜索来获得最优解.当惯性权重ω取值较大时,全局搜索能力强;较小时,局部搜索能力强.所以,该算法的惯性权重通常是线性递减的[2].

假设：所要优化问题的种群大小为n,解空间维数为m,种群中每个粒子的位置为Xi(i=1,2,…,n),每个粒子的适应度值为f(Xi)(i=1,2,…,n),第k代中第i个粒子的位置为Xik,粒子的速度为Vik,第i个粒子得到的最优适应度值的位置为Pik(i=1,2,…,n),所有粒子中得到最优适应度值的位置为Pgk.公式(3)、公式(4)为标准粒子群优化算法中对于第k代粒子的速度、位置更新公式：

其中,ω为惯性权重,一般为线性递减,运算方法见公式(5).

也有研究者使用一种基于对数递减的惯性权重运算方式[21],见公式(6),一般取值由0.9递减到0.4[22]：

其中,ωs为起始惯性权重值,ωe为结束惯性权重值,Tc为当前迭代深度,Tm为最大迭代深度.

除此之外,还有许多其他有关惯性权重的修改方法.例如指数递减策略[23]、自适应惯性权重[24]等,在此不做详细介绍.

SPSO算法的大致思路为：粒子群中每个粒子都有自己的位置及速度,每次迭代就相当于更新了群体中每个粒子的位置和速度,粒子的速度更新与粒子前一次速度及自身历史最优位置和群体历史最优位置与当前自身位置的差值有关,粒子的位置更新与速度有关.而 SPSO算法的特点是对于粒子的继承能力部分,添加了一个惯性权重,以此来改变粒子历史速度属性对于当前属性的影响能力.其主要思想为：在优化算法刚开始时,通过较大的惯性权重来使得粒子群的全局搜索能力强于局部搜索能力,而在算法不断进行迭代优化之后,通过减少惯性权重来逐步加强粒子群的局部搜索能力.

1.3 带收缩因子的粒子群优化算法

带收缩因子的粒子群优化算法(standard particle swarm optimization with a constriction factor,简称PSOCF)流程与最初的PSO算法相似,区别在于粒子的速度更新公式不同.PSOCF运用收缩因子来对每次更新后的速度进行压缩,从而提升收敛速度.

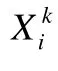
其中,φ为收缩因子.

与 SPSO算法不同,该算法的收缩因子不仅仅是改变了自身历史速度的影响能力,同时也改变了历史最优位置对粒子速度的影响能力.由于收缩因子是固定常量,为了能够较好地平衡全局搜索与局部搜索之间的权重,一般使用公式(9)来计算收缩因子常量[3]：

PSOCF算法的特点是对于粒子的继承能力、自我认知能力及社会认知能力部分,添加了一个压缩因子,因此与SPSO算法相比,PSOCF算法在速度更新方面会更快地趋于稳定.其主要思想为扩大了惯性权重的影响范围,因此PSOCF算法全局搜索能力的减弱速度以及局部搜索能力的增强速度都得到了提升,从而提升了整体算法的收敛速度.

2 新的带多级扰动的混合型粒子群优化算法

SPSO和PSOCF这两种改进优化算法各有特点.在粒子群算法中,不同的参数影响着算法不同的方面：惯性权重影响的是算法中粒子属性的继承性;而压缩因子不仅影响继承性,更影响了整体算法的收敛性.压缩因子过大,收敛性差,且算法接近于随机搜索优化;压缩因子过小,则易提早收敛,导致结果可能为局部最优值,精度下降.从针对粒子进行分层[24]得到灵感,本研究提出的新型改进算法——带多级扰动的混合型粒子群优化算法(mixed particle swarm optimization with multistage disturbances,简称MPSO),是将以上两种优化算法的优点进行整合,在考虑粒子能够较好继承自身最优解和群体最优解的基础上,引入多级扰动来增加粒子位置变异的随机性以及防止粒子的早熟收敛.

粒子群优化算法具有收敛快的特点,使得算法容易陷入局部最优值而使得最终优化结果产生误差,因此在本研究中引入多级扰动来防止早熟收敛.多级扰动策略分为两级：一级扰动的主要作用是使粒子能够更充分地遍历解空间,类似于混沌扰动[25],都是为了增加粒子的遍历能力;二级扰动则是为应对在多峰值情况下易陷入局部最优值的问题而提出的辅助策略,提高搜索结果的精度,类似于蜜蜂寻找蜂蜜.目前已寻找到暂时最佳的,但是仍需要再去其他地方探索观察是否有更为丰富的蜂蜜,那么便假设此时刻的最优位置的食物已耗尽,以此为基础再去寻找其他食物[26].一级扰动在粒子更新位置之后引入.具体的引入概率与当前迭代深度(Tc)及最大迭代深度(Tm)有关,见公式(10).

其中,ε为引入一级扰动的概率.得到的概率会随着迭代深度的增加而减少.与此方法类似的是将粒子分为两种：一种负责标准运行,另一种负责群体多样性.将两种粒子进行结合,可以趋近粒子在探索和收敛间的平衡[27].二级扰动在一级扰动判断之后引入.是否引入二级扰动,与粒子是否早熟的判断有关：若在优化过程探索期中最优粒子连续出现10次相同状态(前期实验表明：触发二级扰动的相同次数分别为10,20,30,40时,精度都没有显著差异(见表1),因此设置为10次),则判定为局部收敛(早熟),从而引入二级扰动,使粒子快速跳脱出局部最优值.

MPSO算法主要是将优化过程的中前期定义为探索期,尽量保持较强的全局搜索能力;而在优化后期,为了快速收敛,尽量加强局部搜索能力.结合前述两种经典优化算法的优点：探索期中利用惯性权重及一级扰动A(后文公式(12))在优化前期较强的全局搜索能力,尽可能的去遍历解空间,并使用二级扰动来摆脱局部极值;在优化后期,则使用收缩因子及一级扰动B(后文公式(13))来增强粒子的局部搜索能力,从而完成收敛.

Table 1 Result of four optimization algorithms for different second disturb condition of five test functions表1 4种优化算法对于不同二级扰动条件的5种测试函数的优化结果

基于与前述现有算法相同的假设,MPSO算法具体优化流程如下.

Step 1. 初始化粒子群中所有粒子的位置和速度.

Step 2. 计算每个粒子的适应度值.

Step 3. 对于每个粒子,将此次优化得到的适应度值与其自身经历过的历史最优适应度值Pik进行比较,若优于Pik则更新该粒子的历史最优位置.

Step 4. 当所有粒子都更新粒子历史最优速度Pik之后,将每个粒子的适应度值与整个群体的最优值Pgk进行比较,若优于Pgk的适应度值,则对Pgk进行更新.

Step 5. 根据当前迭代深度判断使用公式(3)、公式(4)还是公式(7)、公式(8)对所有粒子更新速度及位置.

Step 6. 更新适应度值.

Step 7. 根据公式(10)判断是否引入一级扰动：若引入扰动,则到Step 8;若不引入,则到Step 9.

Step 8. 引入一级扰动后再次更新适应度值：若新适应度值优于原适应度值,则保留扰动;否则删除扰动.

Step 9. 判断当前收敛状况是否满足提早收敛的条件：

➢ 若满足,则引入二级扰动,并回到Step 5;

➢ 若不满足,则判断是否满足终止条件：若满足,则结束算法;若不满足,则回到Step 3.

第5步中的速度、位置更新算法有两个：首先使用的是标准粒子群优化算法的公式(3)、公式(4),之后再使用带收缩因子的公式(7)、公式(8).之所以选择这种更新方式,是因为这两种公式各有特点.例如,SPSO对解空间的探索好,而 PSOCF的收敛速度快.所以定义中前期为探索期,中后期则可根据情况实现收敛.将其两者结合在一起,可使优化过程尽量彻底且全面,同时又能及时得到收敛得到优化结果.MPSO算法流程如图1所示.其中的一级扰动的算法流程如图2所示.

探索期时间点的定义,主要由通过一系列的前期预备实验确定.要确定切换时间点,主要考虑算法的两个因素：探索范围的大小及探索最终结果的精度.由于探索范围与迭代深度正相关,因此将探索最终结果的精度作为首要评价标准,在结果精度无显著差异的情况下,将探索范围的大小纳入评判依据.

最佳切换时间的获取也是一个优化问题,因此,将算法中的切换时间点作为优化目标,通过使用本文提出的混合型粒子群优化算法来获取最优解.由于获取最佳切换时间的算法执行中还会涉及探索期切换的最佳切换时间设置,因而为简化起见,将最佳切换时间优化过程中的当次迭代深度的探索期切换时间设置为前次迭代探索到的最优解.本研究运用Sphere函数、Ackley函数、Rastrigin函数、Styblinski-Tang函数、Duadric函数和Rosenbrock函数进行仿真实验,因此也对这6个测试函数的优化来获取最优的探索期切换区间.

对这个子问题的优化过程的具体设置是：把切换时间点所处的算法总体迭代过程归一化为[0,1]区间(将区间归一化是因为在不同优化问题中,得到的范围是不确定的,精度也是不确定的,因此为了拓展算法的通用性,将整体区间进行归一化处理);设定优化算法中粒子个数为 10,粒子维度(探索步长)为 10;时间点探索迭代深度为100;函数极值探索的迭代深度为2 000;以对不同函数探索到的极值精度(或偏差度)作为适应度函数,评价比较切换时间点优劣.优化结果显示,对所有函数来说,最优值(即极值)探索到的时间点基本上都在10/20～12/20之间(即迭代深度1000～1200).具体对比结果见表2.

Table 2 Optimization algorithm for the same dimension of the six test functions for the time switching point表2 优化算法对于相同维度的6种测试函数的时间切换点优化结果表

考虑算法存在的系统误差以及一定的随机性因素,将算法的切换时间点定义到合适的范围区间.从表 2的结果,确定该区间范围为[1/2,3/5].

本文提出算法的迭代深度到达切换时间区间后,通过判断当前最优值第 1次出现的迭代深度来确定本次优化探索期结束的时间点.因此,本研究提出了公式(11),使得能够方便地在归一化后的区间找到时间切换点T：

其中,Tf为当前最优值第1次出现的迭代深度,Rsa为归一化整体迭代过程中切换时间区间的开始,Rst为切换时间区间的结束.

为了针对不同状态和特点的粒子,算法中所引入的一级扰动分为两种不同的形式,记为A和B(如图2所示).

· 一级扰动A在优化前期引入,主要作用是增大粒子对本身邻域的探索能力;同时,reset保证了粒子有突破当前局限的可能性;

·B部分在算法后期引入,主要作用是对粒子位置进行小幅度的探索修正.

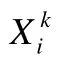
其中,r0为[-2,2]之间的随机数,有关r0的取值将在本文下文中进行验证;T为通过公式(11)获得的时间切换点;r1,r2,r3为[0,1]的随机数;ga为标准高斯随机数(μ=0,σ=1,在[-3,3]的概率为99.8%);reset表示对当前粒子的位置在当前解空间中进行随机重置.一级扰动A和B中是两种不同的扰动方式,在具体实施中选择其一进行,且两者选择概率是相同的.每次引入一级扰动之后,都要检测当前引入的一级扰动是否使得适应度值更优：若更优,则保留此次一级扰动;否则,删除当次扰动(避免无用扰动对结果产生影响).

算法中对粒子陷入局部最优的判断：如果粒子连续10次的状态都相同,那么便定义当前粒子陷入了局部最优值.若已陷入局部最优值,则会引入二次扰动.二级扰动主要是将粒子的位置重置为与当前局部最优结果有关的位置(见公式(14)),并且让其脱离当前局部最优.但脱离结果不能过于随机,因此运用了基于最优位置值附近的随机位置分布,来更新粒子位置,从而达到脱离的效果：

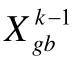
前述公式中,包含两个随机数r0和ra.这两个参数在整个算法中,目的是增强粒子的探索能力和跳脱出局部最优值的能力,因此其取值对优化算法的改进比较关键.在本研究中,运用了一些前期预备实验对这两个随机数的取值范围进行探索.实验中,首先设置了一个前提假设：这两个随机数的取值范围是基于 0对称的;随后,选择不同的上下限范围,并对研究中涉及的测试函数(Sphere函数、Ackley函数、Rastrigin函数、Styblinski-Tang函数、Duadric函数和Rosenbrock函数)进行预运算;最后,对不同取值范围下的优化结果进行评判.表2中列出了不同取值组合设置下的优化结果优劣比较——选用了[-2,2]范围作为基准,将其他取值范围的优化结果与[-2,2]的优化结果作对比.

· 若优化结果比基准要好,则认为该取值范围更优;否则,记为更差;

· 在极值为0的测试函数优化中,若收敛精度差值不超过1,或者在极值非0的测试函数仿真中收敛误差不超过1,则记为无差异;

· 基准本身不进行自身对比.

另外,在对不同的参数范围进行比较时,我们将最优值为0的函数占最终结果的比重为0.5,最优值不为0的函数占最终结果的比重为0.5.由此,从表3中可以得出结论：当r0,ra取值[-2,2]时,对于最优值为0以及非0的情况的综合效果最好.

本研究中所引入的多级扰动机制,实质是在相对稳定的优化过程中加入随机性和变异性,并且针对于仍未跳出局部最优值的情况,提供了二级扰动,把粒子进行大幅度的移动,从而摆脱当前局部最优值的影响.若二级扰动引入后仍陷于局部最优值,则再次引入二级扰动….以此递进,最多可进行64次(前期实验表明,重复引入二级扰动的次数在16,32,64,128这4种设置下,除Sphere函数外,其余的函数都不能体现出显著差异.而Sphere函数则是在64次重复引入的情况下,优化结果精度最高(见表4),因此,这里设置为64次).这是为了能在陷入无限循环之后,从其中跳脱出来的同时又能尝试引入多次扰动来摆脱局部最优.

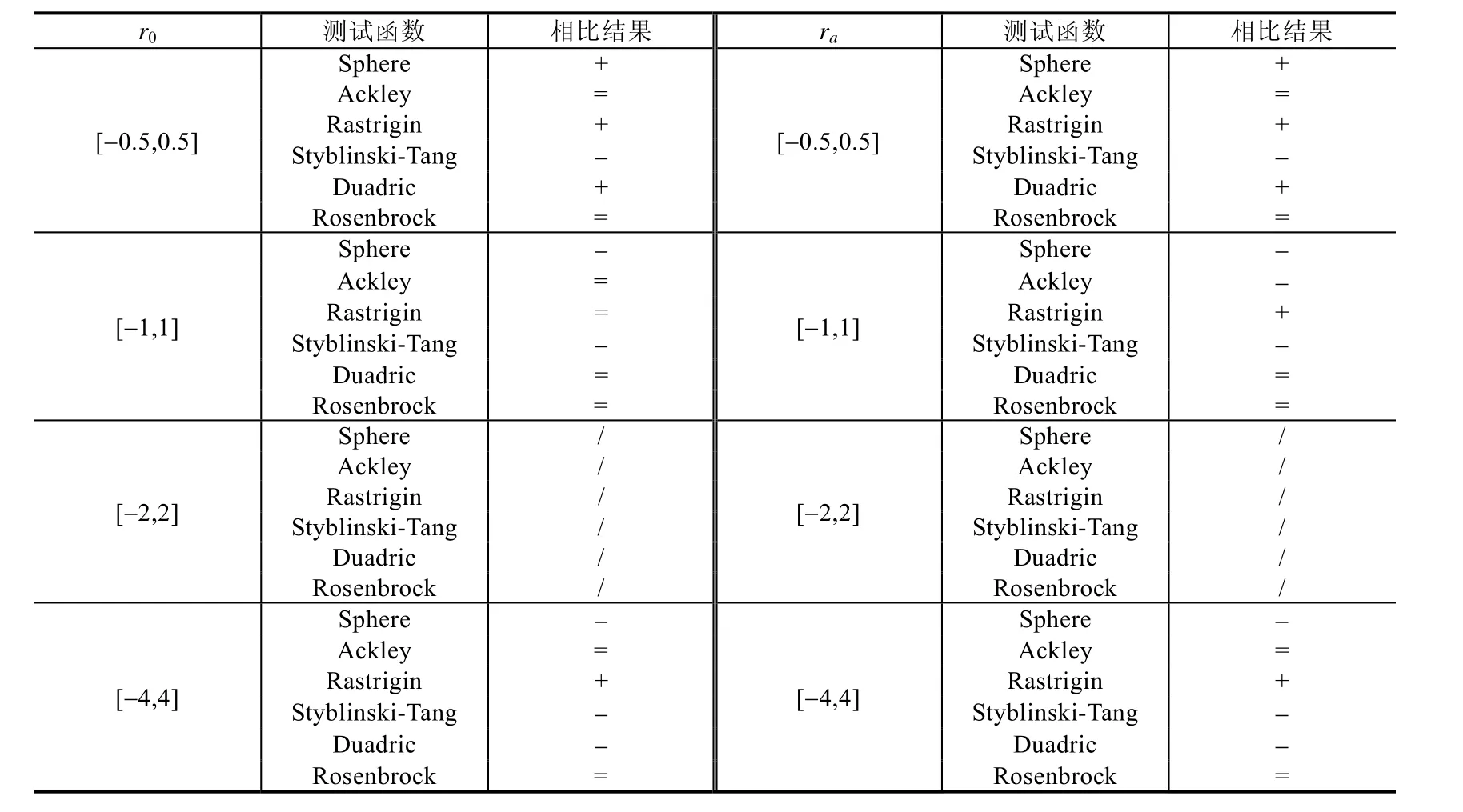
Table 3 Result of different r0 & ra to optimization algorithms for different dimension of sixtest functions表3 不同r0 & ra的MPSO算法对于对于不同维度的6种测试函数的优化结果表

Table 4 Result of four optimization algorithms for different max number of second disturb of five test functions表4 4种优化算法对于二级扰动不同最高次数的5种测试函数的优化结果表

本研究使用了异步粒子群优化算法的粒子更新方式[28].同步粒子群优化算法的粒子更新方式是在一轮粒子全部更新得到适应度值之后,再更新粒子最优及群体最优.而这种异步的形式是在搜索中,当任意一个粒子发现其计算的适应值优于共享信息中的适应值时,则立即更新共享信息,以此提高粒子的利用效率.同时,粒子群算法根据邻域内粒子数量的不同,可以分为全局和局部两个形式[1]：全局版本就是所有粒子都是其中某一颗粒子的邻域成员,局部版本就是只有一部分粒子是某一颗粒子的邻域成员.对于简单的问题,邻域内的粒子越多,效果越好;对于复杂的多模问题,邻域内的粒子越少,效果越好[29],除此之外,还要一些其他的定义方式,如 4类结构、金字塔结构[28]、可变多簇结构[30]等.MPSO采用的是异步全局粒子群算法的形式.

在对指定优化问题进行优化时,粒子的运动范围往往都是限定的,因此需要对超出限定阈值的粒子进行处理,处理方法一般有吸收墙、反射墙、衰减墙和隐匿墙[31].本研究运用了重置的方法——将超出阈值的粒子重置在阈值边界附近,此方法近似于反射墙,但是反射能力被大大削弱,可称为弱反射墙.假设当前问题限制的粒子阈值范围为[-α,α],那么结合反射墙及衰减墙,可将弱反射墙的运算定义为如公式(15)所示形式：

其中,r4为[0,1]之间的随机数.

算法整体的时间复杂度由原本的O(n)变为O(cn),其中,c为一个常数(c＞1),取值与引入扰动的次数呈正相关;n与粒子维度d、种群粒子数m、最大迭代次数t有关.

3 算法仿真实验

在本研究中,为了测试MPSO算法的有效性,选择了6个函数——Sphere函数、Ackley函数、Rastrigin函数、Styblinski-Tang函数、Duadric函数及Rosenbrock函数来进行测试.同时,运用现有的3个改进PSO算法——SPSO,PSOCF和 PSO-DT[32]进行相同条件的优化运算,再将三者的优化过程与结果进行对比与验证.仿真实验在Windows 10平台中Eclipse环境中进行,硬件配置为Inter i5-2430M,RAM 4GB.

3.1 测试函数

1. Sphere函数.

函数在xi=0时达到全局最小值0,为单峰值函数.函数表达式见公式(16).

2. Ackley函数.

函数在xi=0时达到全局最小值0,且函数在解空间中存在大量局部极小值点.函数表达式见公式(17).

3. Rastrigin函数.

函数在xi=0时达到全局最小值 0,且函数在解空间中存在大量的正弦凸起的局部极小值点.函数形式见公式(18).

4. Styblinski-Tang函数.

函数在xi=-2.903534时达到全局最小值-39.16599乘上d(d为维度,表示自变量x的坐标数目),且为多维多峰多局部最优值函数.函数表达式见公式(19).

5. Duadric函数.

函数在xi=0时达到全局最小值 0,为单峰值多极值函数.此函数与 Sphere函数类似,但是考虑了维度因素d(此处同样为自变量x的坐标数目),因此更容易陷入局部极值.函数表达式见公式(20).

6. Rosenbrock函数.

函数在xi=0时达到全局最小值0,为单峰值凹槽型函数.此函数在极值附近的值存在极微小的差别：

在标准粒子群优化算法中,有关参数的设置通常是类似的.一般来说,学习因子c1,c2取值范围为[0,2],在算法中一般取值为2.0,而ω则是从0.9递减到0.4[21],见公式(22).

而在带收缩因子的实验中,发现了当c=c1+c2=4.1,根据公式(7),得到φ=0.729时,PSOCF算法能够较好的平衡探索及收敛能力[3].

因此,在本研究的仿真实验中,设置各个算法的粒子规模n为5,10,15和20;标准粒子群算法中,c1=c2=2;惯性权重ω采用对数递减,从0.9对数递减到0.4;带收缩因子的粒子群算法中,收缩因子φ=0.729,学习因子c1=c2=2.05.

3.2 仿真实验结果与分析

通过仿真实验,对上述4个函数进行优化测试：定义函数的全局极值为最优值;运用3种基于粒子群的优化算法(混合粒子群优化算法、标准粒子群优化算法以及带收缩因子的粒子群优化算法)进行优化运算;算法中,设置4种步长维度(5,10,15和20,表示优化算法中粒子个数)分别进行运算;单次优化的终止条件为迭代次数达到2 000次;实验重复次数为10次,取平均值对不同设置和场景(函数)分别进行比较.前3个函数——Sphere函数、Ackley函数和 Rastrigin函数因其全局最小值都为零,因此优化算法的优化效果以其最终优化结果值的精度表示,具体对比结果见表5.而Styblinski-Tang的全局最小值不为0,因此优化结果以算法优化值与函数极值之间的偏差来表示.偏差φ的计算方法由公式(23)计算而来：

其中,Vt为Styblinski-Tang函数的结果真值,op为优化算法得到的结果值.具体的结果对比见表6.

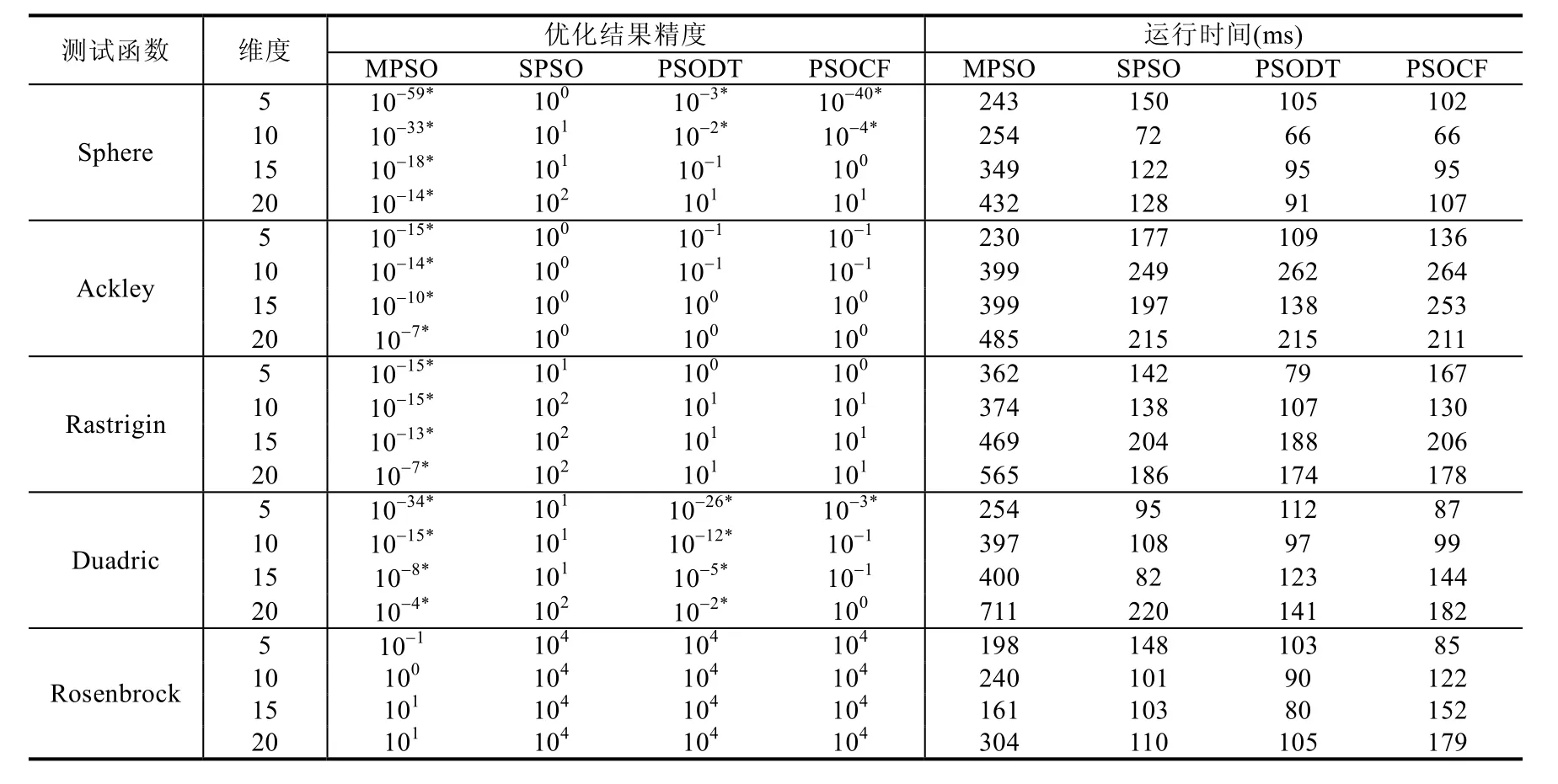
Table 5 Result of four optimization algorithms for different dimension of five test functions表5 4种优化算法对于不同维度类型的5种测试函数的优化结果表

Table 6 Result of three optimization algorithms for different dimension of Styblinski-Tang test functions表6 3种优化算法对于不同维度的Styblinski-Tang测试函数的优化结果表

从表5可以看出,在优化结果精度方面,在所有的4种不同维度设置下,本研究提出的MPSO算法对3种最优值为 0的测试函数的优化结果都显著优于另外两种改进算法的结果;并且在其他算法无法定位到最优值的情况下,MPSO算法依然能够找到最优值,且具有较高的精度.具体来说,在Sphere和Ackley函数上,PSOCF算法也能找到正确的最优值,但是在最后结果的精度上与MPSO算法仍有较大差距;对Rastrigin函数的优化结果来说,PSOCF不能找到正确的最优值,而MPSO的最终结果精度较高;而SPSO算法对这3个测试函数的优化结果的精度都处于最低的位置,几乎都未能定位到最优值.

从维度上来说,随着测试函数维度的提升,所有算法的优化结果精度都相应降低.从表5中可以看出,在实验中设置的维度范围内,本研究提出的MPSO都能准确的找到最优值并保证一定的精度;SPSO算法在此范围内基本上都没有能够找到最优值;PSOCF算法则是在对Sphere函数和Ackley函数的的优化中,以5和10为维度时能够找到最优值并进行一定的精度探索;但在15和20维度,则并不能够找到最优值.

整体优化迭代过程如图3～图8所示.结合图3～图6可以发现,在优化前期(探索期),MPSO算法一直在探索,直到后半期转入低几率弱一级扰动B后开始逐渐收敛,而在切换更新公式后进行了快速收敛;而 SPSO算法则较为稳定,一直在探索,最终并没有很好地收敛在最优值上;PSOCF算法则是在一开始就在最优值附近开始快速收敛;PSODT与PSOCF算法类似,但是最终优化结果的精度在5维度、10维度时没有PSOCF算法精确.同时能够发现,其他3种算法在5维度、10维度的Sphere函数优化时效果较好;在5维度、10维度的Ackley函数优化时效果一般,但还是找到了最优值,但在一定深度之后则趋于稳定,不再继续探索;而在其他情况下则并没有找到最优值,而是在局部最优值附近进行快速收敛.从图中我们可以清楚地发现MPSO算法的特点：在探索期中,以探索为主;在后半优化过程中,以快速收敛为主.这样就能较好地在平衡探索与收敛基础之上,优化到最优值.而从图7能够发现：无论哪种优化算法在维度超过5时,得到的优化结果都不够精确;但对同样的优化问题而言,本研究提出的混合型粒子群优化算法总是能得到精度更高的优化结果.

从时间上来说,本研究提出的MPSO算法中,耗时的主要是引入的多级扰动.因为每次引入一级扰动之后都要重新计算一次适应度值,并因为早熟而引入二级扰动后,重新去引入一级扰动,所以整体时间为原本的2倍～4倍.多出的时间主要为计算适应度值情况下,对原本算法的整体算法流程上所耗费的时间并没有增加,只是增加了一些引入扰动后重新计算适应度值的时间.

从表6可以看出,对最优值不为0的Styblinski-Tang函数的优化测试中,当维度分别为5和10时,MPSO算法的精确度较好;但当维度为15和20时,偏差接近3%.在考虑到真值较大的情况下,这种偏差率可以接受;SPSO算法在维度为5和10时,偏差度达到了3%左右.虽然偏差度有些大,但还在可接受范围;但是在维度为15时,偏差超过了9%;而在维度为20时,偏差更是达到了16%,这表示了偏差过大,优化结果不够准确;而PSOCF算法在测试的维度为 5,10,15中的偏差都超过了 10%,在维度为 20时更是超过了 20%,说明 PSOCF算法对于Styblinski-Tang函数优化能力很差;PSODT算法相对于SPSO和PSOCF算法来说要更为优秀,但其优化精度仍然不如MPSO算法高.结合图8同样也发现,MPSO在前半优化过程中以探索为主,在后半优化过程中以快速收敛为主.这样就能较好地在平衡探索与收敛基础之上,优化到最优值.这也体现了MPSO算法在上述情况下的优化结果都优于其他两种算法,同时,耗费时间大概为其他两种算法的2倍～4倍.

4 结 论

针对经典粒子群优化算法易陷入局部最优及收敛速度较慢等问题,本研究在分析经典的两种粒子群优化算法SPSO和PSOCF的基础上,提出了带多级扰动的混合型粒子群优化算法.原始的粒子群优化算法在多局部极值情况下容易陷入局部最优值.SPSO和 PSOCF算法正式针对这一特点而进行了改进.本研究中提出的MPSO算法结合了这两种经典改进优化算法的优点,引入多级扰动的策略,利用多级扰动干扰粒子探索进程,使粒子在本身速度和位置更新之外,获得了一种“震动”,不但增长了算法对局部极值附近的探索能力,也扩展了算法在陷入局部最优值时的跳脱能力,从而在保证算法及时收敛的情况下,使粒子群优化算法的探索能力和最优值的精度上都得到极大的提升.

通常认为,在PSO相关的算法中最重要的参数是惯性权重和学习因子[33].如何选择、调整这些参数,会直接影响粒子群优化算法的收敛性和结果的有效性.在本文中,粒子更新公式中的惯性权重使用的是对数递减形式.另外,还有其他方法对惯性权重进行递减用以针对不同的优化问题,而如何结合具体优化问题设置不同的惯性权重并加以应用、如何对其他参数进行适应性设置以及如何根据迭代情况自适应的去寻找最优参数,这些都没能在本研究中进行实验和探讨.

本研究中对整个优化周期进行了简单的定义——分为探索期和收敛期.在探索期内,粒子保持跳动能力,对整个解空间进行搜索;而过了探索期之后,则允许其进行收敛.这样的分割对学习因子和惯性权重的应用起到了至关重要的作用.因此,研究中对两个时期的切换时间点做了细致的前期实验,而在后续的仿真实验中,发现前期实验所得的最佳切换时间点所处区间确实很好得平衡了搜索能力和收敛能力.另外,算法中运用的两个随机参数r0和ra,取值对整体算法的优化能力有比较关键的影响.本研究中,在基于经验取值的基础上,对着两个参数的取值进行了不同设置下的对比和前期验证.对于优化算法中的参数取值,总是在不同的应用场景下往往有不同的表现.例如,本文提出的MPSO算法在对间作中的不同作物的间作模式有较好的优化和预测作用,但其与对不同环境下的水稻田间种植模式优化过程的参数设置和适应度函数选取都有不同的策略.因此,很难说在普遍的场景下有一个通用的取值.在这种情况下,运用其他较为成熟和稳健算法先期对参数进行优化是一个比较好的选择.另外,如果能开发出对不同场景自适应调整的智能策略,将能够比较有力地推动优化问题解决及优化算法方面的研究.