☉安徽省滁州市第二中学 张广庆

每一道试题都是有源头的，我们在解题时只要能突破“背景”，构造出合适的基本图形和数量关系，问题就易于解决了.下面以一道模考试题为例，谈谈我的一些粗浅见解，与广大同行共勉.

一、原题呈现

已知梯形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3.

（1）如图1，P为AB边上一点，以PD、PC为边作平行四边形PCQD，请问：对角线PQ、DC的长能否相等？为什么？

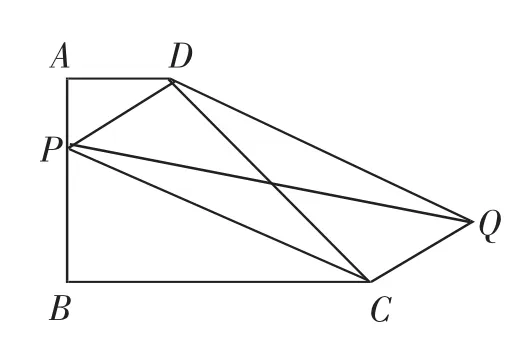
图1

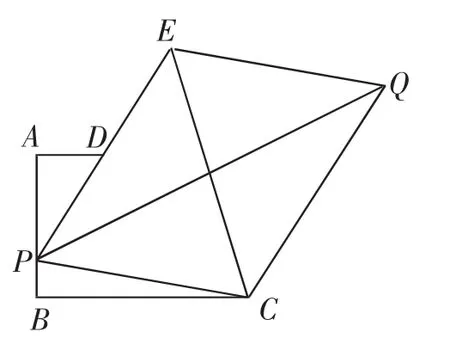
图2

（2）如图1，若P为AB边上任意一点，以PD、PC为边作平行四边形PCQD，请问：对角线PQ的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由.

（3）如图2，若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE、PC为边作平行四边形PCQE，请探究对角线PQ的长是否存在最小值.如果存在，请求出最小值；如果不存在，请说明理由.

（4）如图3，若P为DC边上任意一点，延长PA到E，使AE=nPA（n为常数），以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否存在最小值.如果存在，请求出最小值；如果不存在，请说明理由.

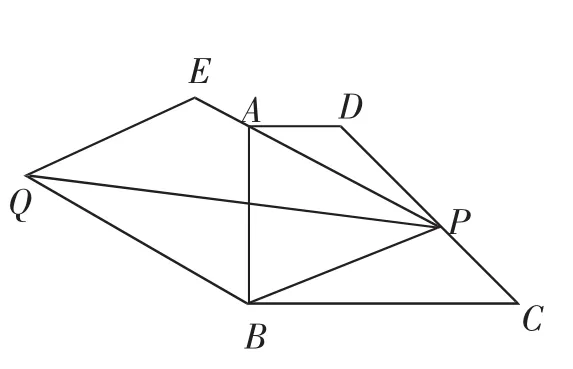
图3

二、解法探究

在解决问题时，首先应弄清问题的背景，获取相关信息；然后基于背景的相关知识展开联想，对信息进行处理、加工，抽象出相关的基本图形和对应的数量关系，从而获得解决问题的路径.

对于问题（1），结合图形和条件，发现直接说明对角线PQ、DC的长能否相等，感到无从下手，我们不妨从结论出发：假设对角线PQ、DC的长相等，则平行四边形PCQD就会成为矩形，从而得到∠DPC=90°.（即当∠DPC=90°时，PQ=DC）现在的问题就是：∠DPC能否等于90°？若∠DPC=90°，一个基本图形——凹槽型（如图4）浮现出来了.（图中的两个直角三角形相似）

设PB=x，则AP=2-x.

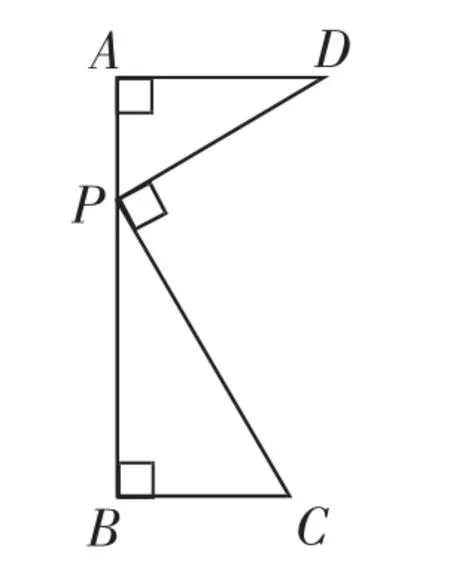
图4

则x2-2x+3=0.而b2-4ac=（-2）2-4×1×3=-8＜0，所以此方程无实数解.

所以假设不成立，即对角线PQ、DC的长不可能相等.

点评：由凹槽型相似，能得到对应边成比例，对应角相等.特别地，当有一组对应边相等时，两个三角形全等.此类图形对于解决一些涉及边的数量关系的复杂图形的题目时有着“柳暗花明又一村”的功效.

对于问题（2），设PQ与CD相交于点O.由平行四边形PCQD，可得PQ与CD互相平分于点O，即PQ=2OP（O为定点）.要求PQ的最小值，可转化为求OP的最小值.其实际背景就是：定点O与定线段AB上任意一点连接的线段中，哪一条线段最短？这样易联想到一个数量关系“垂线段最短”.

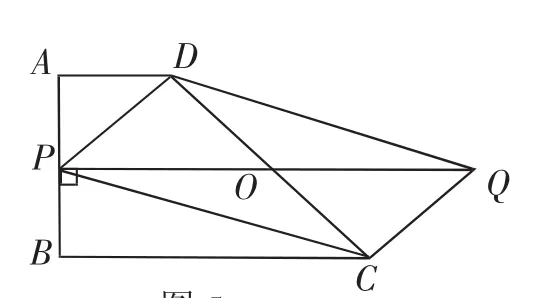
图5

如图5，根据垂线段最短，过CD的中点O作OP⊥AB，垂足为P，延长PO至点Q，使OQ=OP，连接PC、CQ、QD、DP，则四边形PCQD为平行四边形，PQ为所求.

因为AB⊥BC，OP⊥AB，所以PO∥BC.而点O为CD的中点，由平行线分线段成比例定理，得点P为AB的中点，从而OP为梯形ABCD的中位线，则又AD=1，BC=3，所以OP=2，从而得到PQ的最小值为4.

对于问题（3），给出以下两种解法：

解法1：由DE=PD，易联想到三角形的中位线的基本图形，过点E作AD的平行线交BA的延长线于点M.由于定值），易联想到在BC的延长线上补上一段与ME等长的线段CN，这样可把平行四边形PEQC放到以BM、BN为邻边的矩形BNHM中，说明点Q始终在线段HN上运动，联想到一个数量关系“两平行线间的距离最短”（如图6）.

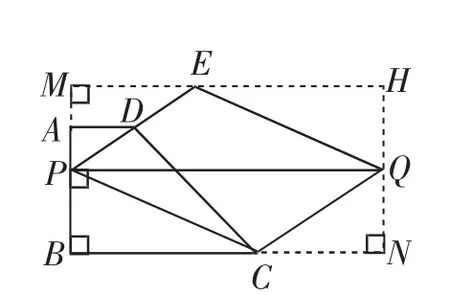
图6

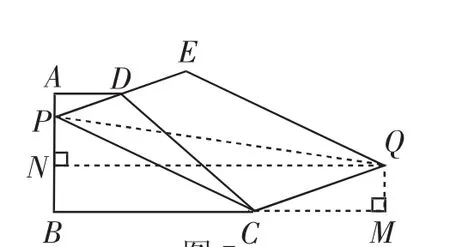
图7

则NC=2AD=2.

所以BN=BC+CN=5.

当PQ⊥AB时，PQ最短.此时有矩形PQNB.则PQ=BN=5.

换一个角度，这道题也可以利用二次函数求最值来解决.

解法2：观察图形发现，随着AP长的变化，PQ的长也在变化，它们之间有没有联系呢？又如何将这些分散的线段集中起来呢？便想到构造一个以PQ为斜边的直角三角形，利用勾股定理表示出PQ，从而利用函数模型求PQ的最值.

如图7，作QN⊥AB于点N，作QM⊥BC，交BC的延长线于点M.则有矩形BNQM.设AP=x，则BP=2-x，其中x的取值范围是0≤x≤2.

对于问题（4），有了解决问题（3）的经验，可以模仿求解，但值得一提的是，PQ不可能与CD垂直，所以采用函数模型求解比较好.（应注意变量PM的取值范围为0≤x≤2）

如图8，设PM=x，则NH=MC=x，AO=2-x，PO=BM=3-x.

由△APO △QBH，可 得 QH=（n+1）（2-x），BH=（n+1）（3-x）.

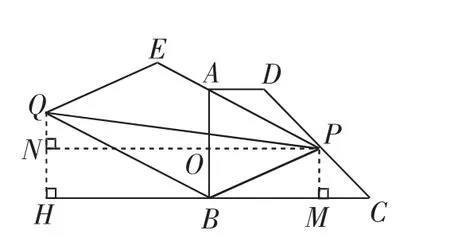
图8

因为a=2（n+2）2＞0，所以当时，PQ2随x的增大而减小.

点评：求线段最值的常用方法：（1）利用性质求最值，如“两点之间线段最短”“垂线段最短”“两平行线间的距离最短”；（2）利用函数模型求最值；（3）利用图形变换求最值……这些方法可以使复杂的问题情境数学化，数学模型便跃然纸上，思路便豁然开朗.罗增儒教授在《解题信息论》一文中指出，数学解题需要：“捕捉信息——弄清题意；提取信息——从“存储机构”中提取出本问题有关的性质、类型（基本模式）……加工信息——将相关信息结合起来，进行加工、重组与再生……”等五个过程.也就是说，拿到一道题，我们应先辨别是否属于已经掌握的类型，如果属于，那就提取出该类型来解答；如果不直接属于，那就进行适当的变化……在日常教学中，我们应指导学生首先弄清问题背景，让他们学会在纷繁复杂的背景中抽象出“模式图形”和“数量关系”，最终实现“有效转化”，探索出解题途径.W