☉江苏省江阴市敔山湾实验学校 夏培培

本文以“几何最值问题”专题课为例，以问题探究为驱动，带领学生进行高阶学习活动，组织学生经历“操作—分析—交流—质疑—创造”的思维过程，使思维从低阶向高阶转化，提升高阶思维能力.

一、高阶思维能力解读

高阶思维是指发生在高层次认知水平上的心智活动.它对应教学目标分类中诸如分析、综合、评价等高层次认知水平的能力，是创新能力、问题解决能力、决策力和批判思维能力的核心［1］.

发展高阶思维需要高阶学习活动予以支持.高阶学习是一种以学习者为中心、开展问题求解的学习活动，是一种形成知识共享、互动合作的学习方式.在“几何最值问题”一节的教学中，笔者以探究为主线，以问题为依托，从基本模型入手，丰富问题背景，带领学生从复杂图形中发现基本模型并与相关思想方法联系，进而拓展学生思维，培养学生的高阶思维能力.

二、高阶思维能力的实践

教学环节1：根据问题情境回顾基本模型、思想方法

问题1：如图1，已知直线l外两点A、B，在l上找一点P，使PA+PB的值最小.

图1

图2

问题2：如图2，已知∠MON外一点A，在OM、ON上分别找一点P、B，使PA+PB的值最小.

生1：对于问题1，以直线l为对称轴作A（或B）的对称点A′（或B′），连接A′B（或AB′）；对于问题2，过点A作AB⊥ON，交OM、ON于点P′、B′.

师：解决最值问题常用的方法是什么？

生2：轴对称变换，旋转变换，平移变换，确定动点轨迹等.

师：解决这两个问题的理论依据是什么呢？

生3：两点之间线段最短和垂线段最短.

设计意图：问题是思维的起点和动力.通过两个元问题带领学生复习回顾解决最值问题的两个基本模型，归纳最值问题的基本构造方法和理论依据.让学生充分理解模型的内涵，并将知识和思想方法相联系，丰富学生的知识结构.

教学环节2：拓展模型和思想方法，探寻思维发散点

问题3：如图3，已知正方形OBCD，点A是OD边上一定点，请你在对角线BD上确定一点P，使PB的值最小.

变式：如图4，在l上找一点P，使得PB的值最小.

图3

图4

驱动性问题1：看到“你想到什么？能否从这个角度出发尝试转化

生4：我想到45°的三角函数值，构造直角三角形.

驱动性问题2：PB为直角边还是斜边？如何构造？

生5：由BD为对角线，得∠DBC=45°.以BP为斜边构造直角三角形（如图5）.

图5

图6

驱动性问题3：如果去掉正方形这一条件（如图6），如何解决？

生6：补出BC这条线，按照刚才的方法.

学生画图探究解决并交流.

生7：在l下方构造Rt△BEP（如图7），其中∠EBP=30°；找到点P′即为所求.

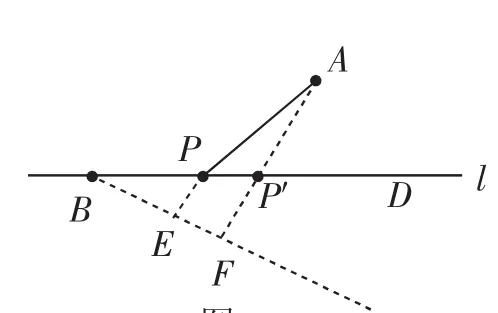
图7

图8

生8：能否在l上方构造Rt△BFP（如图8，∠EBP=30°）？

驱动性问题4：不妨试一试，PA+PB=PA+PE.那么接下来就转化为怎样的问题？

生8：PA+PE的值最小，即将军饮马问题，作E点的对称点，又变为图7的方法.我明白了，因此在l上方构造，最终仍然要对称转化到l下方.

驱动性问题5：若将“PA+PB”改为“PA+k·PB”呢？

高阶思维发展的关键是思维的交互、内省.思维不是自然发生的，但是它一定是由“难题和疑问”或“一些困惑、混淆或怀疑”引发的［2］.学生提出在直线上方构造直角三角形可否解决，此时引导学生进一步思考，发现问题转化为将军饮马问题，需作对称转化到直线下方解决问题.在学生有想法和困惑时，教师予以肯定和支持，让学生体验解决问题方法的多角度、多样性，在探究过程中进行思维的自我调节与省思，从而发展高阶思维能力.

教学环节3：模型应用，产生质疑，进一步拓展模型

问题4：如图9，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C的半径r为2，P为圆上一动点，连接AP、BP，求的最小值.

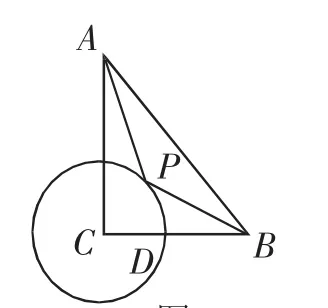
图9

学生提出问题：经过探究发现利用三角函数值无法进行构造转化BP.

驱动性问题6：函数值给我们提供了一个倍分关系，还有什么指示也能提供倍分关系呢？

生10：相似比，即构造相似三角形.

生11：CP=2，BC=4，它们存在2倍关系，由此构造△BCP的相似三角形，在BC上取点D，使CD=1，如图10所示.由，∠PCD=∠PCB=45°，得△PCD △BCP，则则PD=，则

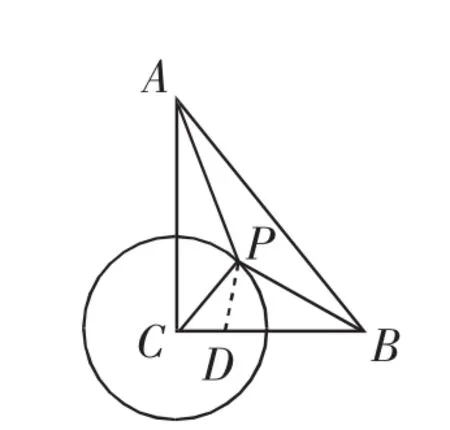
图10

师：非常透彻，通过构造相似比再转化边，在构造相似三角形时需结合题中已知条件之间的关系.

设计意图：利用三角函数转化未能成功解决问题；由此引起认学生的认知冲突，教师充分利用冲突，引导学生打破思维定式、另辟蹊径，探寻转化倍分关系的另一种方法：相似三角形.构造相似三角形在学生思维过程中是一个“逆向”的过程，具有一定的挑战性，教师有必要带领学生一起探究构造方法，感悟构造过程，以此优化学生思维过程的内省与反思.该问题的设计旨在引导学生打破思维僵局，带着质疑和批判去推理和思考，并给予学生充分的时间和机会探索和表达，在潜移默化中提高学生的数学思维品质，培养高阶思维能力.

教学环节4：变式探究，创新优化

变式1：如图9，在“问题4”的条件下，你会求BP的最小值吗？

变式2：如图11，已知扇形COD中，∠COD=90°，OC=6，OA=3，OB=5，点P是CD上一点，求2PA+PB的最小值.

图11

设计意图：课后研究是课堂的延伸，给出两个变式让学生在不同倍分关系和图形环境中探究解决问题的策略，让学生经历知识、方法的再认识和再创造过程.

三、培养学生高阶思维能力的教学思考

1.精心设计问题，培养几何直观

认知心理学认为，“问题”是思维活动进行的原动力和牵引力.问题的设计关系到学生思维的深度和广度；教师的思维结构观念也影响着学生图形与几何的学习走向和效果.因此教师在备课时，要根据学生当前的认知结构，认真研读教材，把握知识体系，关注知识和方法的形成过程及学生的学习心理图式，从而精心设计新知识的“逻辑关联点”，引导学生自我构建知识网络，提升图形与结合思维结构水平，促使学生高阶思维能力逐级跃升.

2.关注策略的形成，加强方法的积累

在解决问题的过程中，需重视解题策略的形成，关注问题的解法和结论.策略的学习无法通过直接的传输获得，需要学生在画图、操作、猜想、实践中发现问题、提出问题、分析和解决问题，从而总结、反思，提炼相应的方法、技巧、经验，真正形成解决问题的策略.当然，策略的形成离不开方法的支撑，方法不是指一个特定的解题技巧，而是解决一类问题的通性通法，它在解决问题的过程中发挥着不可替代的作用.实践证明，通过策略培养、方法养成积累的数学能力更利于学生的思维生长.

3.学会等待，静待花开

在专题课的教学过程中，教师要舍得留时间给学生大胆尝试，找到问题的核心所在.探究尝试的过程，就是发展思维的过程.解决问题后也应留时间让学生进行反思，将探究经验内化为自己的数学素养.内化的过程，就是自我提升的过程.专题课的着眼点应放在学生学习能力发展上，让学生通过课堂学习，创新数学思维方式，积累解决问题的方法，提升优化意识.

当然，数学思维能力的培养不是一蹴而就的，这需要教师在平时的教学过程中摒弃传统的“授受”模式，为学生思维独立性和创新性培养创造条件，使学生的潜能和创造性得到发挥，以期提高其高阶思维能力.