☉江苏省昆山市正仪中学 金洁霞

折叠问题是初中数学考查的重点和难点，这类问题能够较好地考查学生对轴对称图形性质与规律的学习水平，这类问题对学生的观察、动手和综合应用方面的能力要求高.正因如此，折叠问题一直得到命题专家的青睐，成为各类初中数学考试的热点问题.本文以一道典型折叠问题及其变式为探究载体，重点剖析其内在本质规律，探究其思维路径，体现“异曲同工，万变归宗”的数学哲学之美，旨在抛砖引玉，以期引起教育同仁的进一步思考与探究.

一、折叠问题的案例及变式呈现

案例：如图1所示，矩形ABCD中，AB=6，BC=9，E、F分别是AD和BC上任意两点，线段EF将矩形分成左右两部分，先将右部分沿着EF折叠，恰好使得C点落至AB边上的C′点处，且AC′=BC′，D点变为D′，连接C′D′交AE于M点，试求AM的长度.

思维路径：Rt△MAC′中只有AC′=3可直接得出，而直接在Rt△MAC′中利用勾股定理或三角关系求解AM的长度所需条件不够，需考虑构建与其他三角形的关系求解. 据折叠原理和几何图形关系得：FC′⊥MC′，FC′=FC，则Rt△FBC′Rt△C′AM，即在Rt△FBC′中，运用勾股定理可求出BF=4，则

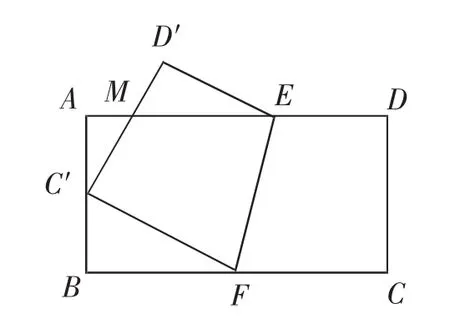
图1

图2

变式1——改变折叠背景

题目：如图2所示，正方形ABCD的边长为6，E、F分别是AD和BC上任意两点，线段EF将矩形分成左右两部分，先将右部分沿着EF折叠，恰好使得D点落至AB边上的D′点处，且AD′=BD′，C点变为C′，连接C′D′交BF于M点，试求Rt△D′BM的周长.

思维路径：变式1用正方形代替原矩形作为折叠背景，求周长代替求边长.但从数学对象的基本关系的本质看没有新的变化，因此仍然由勾股定理求AE和ED′，再用Rt△D′BM Rt△EAD′求D′M和BM，最终可求Rt△D′BM的周长.

变式2——改变折叠对应点

题目：如图3所示，矩形ABCD中，AD=12，CD=18，E、F分别是AB和CD上两点，将矩形沿着EF折叠，C点落于A点，B点落至B′点，试求S△AEF的值.

思维路径：据题意可知只需求出AE的长度即可得这一面积.据折叠原理可知AF=CF，AB′=BC=12，由几何关系可知△ADF AB′E，即AE=AF.在Rt△ADF中，运用勾股定理得AF=13，则12=78.

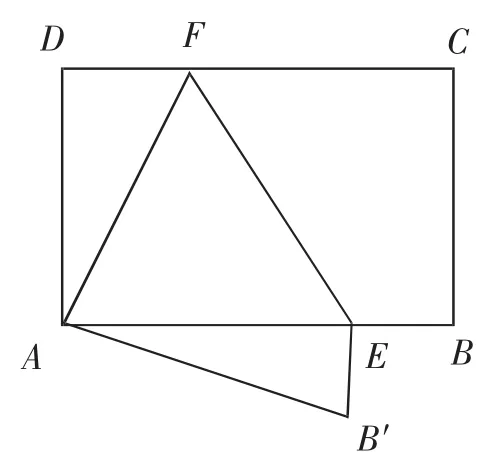
图3

图4

变式3——改变折叠对应边

题目：如图4所示，矩形ABCD中，AB=2，E、F分别为矩形ABCD中AD和CD的中点，现将△ABE沿着折痕BE进行折叠，点A恰好落至BF上的A′点，试求AD的长度.

思维路径：根据矩形性质，AD=BC.根据折叠性质，可得A′B=AB=2，△EDF △EA′F，即则BF=A′B+A′F=3.在Rt△BCF中，根据勾股定理，可得

案例及变式的“归宗”分析：在以上案例及变式中，其形式可以是千变万化的，但是其命题立意与问题解决的源流可以归宗为折叠变化的基本关系——全等关系、对称关系；而折叠背景则提供了具体的数量计算路径.因此，这类折叠问题为同源同宗的衍生问题.

二、折叠问题的数学教学过程思考

1.立足基本数学关系，奠定折叠问题解决的基础

（1）重视几何关系作为解决折叠问题的直接工具作用.首先，要重视几何关系的梳理与教学：几何图形的折叠属于轴对称现象，关于折痕对称的两个图形中对应线段长度相等、对应的两个角度相等，初中数学折叠问题往往建立在“平行四边形、矩形和正方形”等背景之上，在处理此类折叠问题时应该弄清折叠的背景，解题过程中灵活运用其对应的性质.

折叠问题中求解线段长度、角度大小、几何图形的周长等问题，往往涉及三角形相关知识：直角三角形中的勾股定理、直角三角形中两个锐角互余，等腰、等边三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质，平行线性质、中位线性质、角平分线性质、垂线定义等.解决实际问题时存在一定的内在规律：对于直角三角形中的长度求解，可以利用勾股定理，对于一般三角形中的边长，可以利用全等或相似的手段进行求解.

（2）以数学思想的教学提升折叠问题教学的价值.折叠问题在平面、空间、直线上的数量关系，往往涉及较丰富的代数关系，函数思想、方程思想等数学思想，可以借助折叠问题背景进行渗透式教学，从而可设计归宗于折叠但不拘泥于折叠的教学处理，提升折叠问题教学的数学教育价值.如上述典型案例中的化归思想体现在：AM长度的求解，借助Rt△FBC′Rt△C′AM进行间接求解；方程思想体现在：案例分析过程中BF长度的求解，将BF作为未知量，运用勾股定理构建方程进行求解.

数学解题离不开数学思想的理论指导，数学思想的灵活运用，有助于学生迅速探寻数学解题的思路，有助于学生获得有效解题方法的灵感.对于初中数学教师而言，在解题教学实践中，摆脱“就题论题、机械讲解方法”等传统教学方式的束缚.实践表明，数学思想是数学解题教学的“内功”支撑点，离开数学思想的数学解题教学，必定是“肤浅、表面”的数学教学，不利于学生数学解题能力的提升，不利于学生数学学科核心素养的提升.

2.构造折叠问题实例，提升学生数学素养

众所周知，恰当的实例可以为学生问题解决过程的尝试与素养形成提供练手.因此，教师需要发挥教学智慧构造实例，充分展示处理折叠问题的具体思想与方法.

实例：如图5所示，矩形ABCD中，AB=3，BC=5，E为CD边上任意一点，若以BE为折痕，将△BCE进行折叠，C点落至AD上的F点，试求线段CE的长度.

图5

解析：根据折叠性质可知BF=BC=5，EF=CE，在Rt△ABE中假设CE=EF=x，则DE=3-x.DF=AD-AF=5-4=1.在Rt△EDF中，根据勾股定理，可得即即

点评：本题是以矩形为背景的折叠问题，解题中主要体现折叠性质、勾股定理、转化思想、方程思想的灵活运用，解题过程清晰、简练.

三、结束语

数学的形式千变万化，而对其进行溯源，往往不同形式出于一宗.因此，数学教学有必要深度挖掘教学素材的数学源流，力求教学过程贯通规律探究与思维形成训练.初中数学折叠问题中，不管问题形式如何变化多端，只需要准确抓住折叠问题的“宗”——折叠的本质（轴对称的性质），引导学生有机融合相关的数学知识和数学思想方法，使其达到举一反三的学习效果，对难题能有自己的数学思想与解决方法，进而促进初中学生数学素养的不断提升.