唐建华 张永政 刘晓媛

摘 要：针对漏磁数据的稀疏化过程，观测值数量与漏磁数据稀疏性对重构准确率的影响，设计了基于压缩感知的管道漏磁检测数据稀疏化方法。通过实验对比由不同观测矩阵进行漏磁数据稀疏化的性能，总结出数据稀疏度和观测值的数量对重构准确率的影响，选出不同类型漏磁数据适用的观测矩阵，最终设计出基于压缩感知的管道漏磁检测数据稀疏化方法。

关键词：压缩感知;观测矩阵;稀疏化方法

中图分类号：V241.4 文献标识码：A 文章编号：1671-2064（2019）06-0066-02

0 引言

本文主要基于压缩感知的管道漏磁检测数据的稀疏化方法研究，文章分析了几种常见的观测矩阵，并对漏磁数据实施稀疏采集，通过实验选择了合适的观测矩阵。最终通过运用压缩感知理论设计了漏磁数据的稀疏化方法，该方法简单清晰，易于实现，能够有效节省计算资源，压缩速度更快。

1 不同观测矩阵下的稀疏化处理

1.1 信号的稀疏性

通常自然界中的信号不是完全稀疏的，而是在某种变换域下，将其看成近似稀疏，也可以说该信号是可压缩的[1]。理论上任何信号都是可以压缩的，前提是找到与信号特征相对应的稀疏表示空间，这样就可以进行稀疏化处理，实现信号的稀疏化。同样的漏磁检测数据也是一种信号，可以找到一种稀疏变换基，使其成为可压缩的。

稀疏表示[2]指漏磁信号在某个变换域下是稀疏的，也就是其用该域下基向量来表示时许多系数为零或者接近零，另外基向量之间是正交的。稀疏变换基不能自适应，需要根据信号的不同情况，选择最适合的。

1.2 观测矩阵

在压缩感知方法中，随机高斯观测矩阵[3]的使用最为广泛，其构造方法为：设计一个大小为M×N的矩阵，使得Φ中的每一个元素都独立服从均值零，方差为1/M的高斯分布。该矩阵的随机性很强，当其观测值的数量时，有极大的可能会满足RIP准则。

随机伯努利观测矩阵[4]和随机高斯观测矩阵的性质类似，其构造方法为：设计一个大小为M×N的矩阵，使得Φ中的每一个元素都独立服从伯努利分布，与随机高斯观测矩阵相同，随机伯努利观测矩阵同样有较强的随机性，它的观测值数量时，会有极大概率满足RIP准则（c为极小的常数）。

哈达玛（Hadamard）矩阵是由+1和-1元素构成的。部分哈达玛矩阵的构造方法为：首先生成一个N×N大小的哈达玛矩阵，之后随机从其中选取M行向量，构成一个大小为M×N的观测矩阵。因为哈达玛矩阵为正交矩阵，从中选取的矩阵同样有非相关性和部分正交性。因此，同其他确定性观测矩阵相比，该矩阵在重构时所需的观测值数量M较少，同等条件下，重構出的信号效果更好。但是哈达玛矩阵的维数N必须满足2的n次幂，这限制了其使用的领域。

部分正交矩阵同样应用到了观测矩阵中，前文的部分哈达玛矩阵便是部分正交矩阵的特例。部分正交矩阵的构造方法为：首先生成一个N×N大小的正交矩阵U，然后从矩阵U中随机选取M行向量，最后对M×N大小矩阵的列向量进行归一化处理，即可得到观测矩阵。

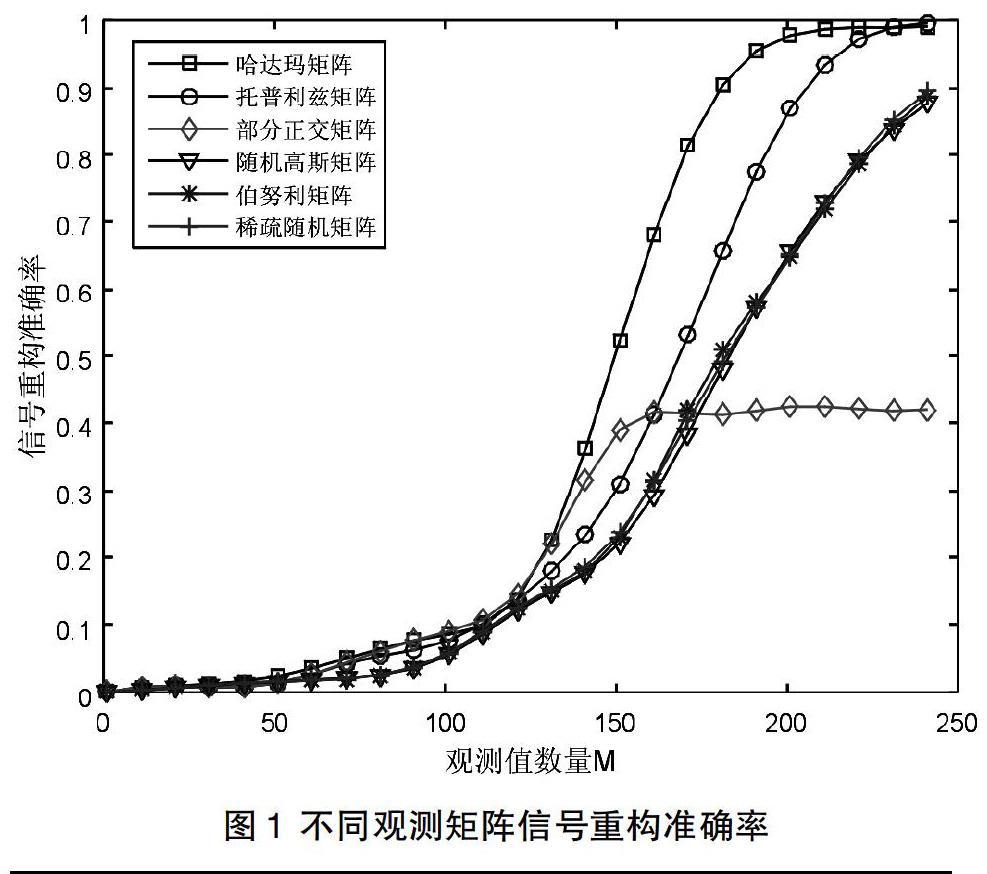
稀疏随机观测矩阵的构造方法如下：设计一个大小为M×N的矩阵Φ，所有元素置0，并且M

托普利兹和循环矩阵的构造方法为：首先生成一个随机向量u=（u1，u2，…，uN）∈RN，接着用生成的随机向量Φ，经过M（M

1.3 观测矩阵稀疏化处理过程

采用压缩感知的方法过程中，通过观测矩阵获得观测值和信号重构起到了重要的作用，也是压缩感知过程的主要内容。因此，观测矩阵是压缩感知中极为重要的部分，如果信号重构的算法不变，它性能的好坏直接影响到重构信号与原始信号间差值的大小，即观测矩阵直接影响着信号重构的质量。

稀疏度K值一定时，观测值数量M的值越大，信号能够被精确重构的概率则越大。当观测值的数量增加到一定程度，大部分稀疏度的信号能够被完全重构。取一段10米长的管道漏磁检测数据，通过以下几种不同的观测矩阵对其进行稀疏化处理，单次处理的数据长度为N=256，观测值的数量M=75，如此循环，最终得到的稀疏化处理后的漏磁数据。随机高斯观测矩阵，压缩率达到30.08%;随机伯努利观测矩阵，压缩比达到29.35%;部分哈达玛观测矩阵，压缩比达到29.31%;部分傅里叶观测矩阵，压缩比达到33.27%;稀疏随机观测矩阵，压缩比达到31.22%;托普利兹和循环观测矩阵，压缩率达到29.46%。

2 观测矩阵稀疏化效果比较分析

2.1 不同观测矩阵重构准确率比较

为了准确选合适的观测矩阵，根据管道漏磁数据的特点，选择长度为N=256，稀疏度K=64的信号，采用不同类型的观测矩阵，进行稀疏化处理，观测值的数量为M∈{25，50，75，100，125，150，175，200，225}，利用正交匹配追踪算法进行重构，结果如图1所示。

从图1中可以看出，对同一信号，观测值的数量M越大，信号能够被重构的概率越大，当取值达到一定大小时，信号可以完全重构出来。这六种观测矩阵中，哈达玛矩阵重构出的效果最好，部分正交矩阵最差。随机高斯矩阵、伯努利矩阵和稀疏随机矩阵的性能相似。

2.2 不同观测矩阵重构性能指标比较

为了验证不同观测矩阵对漏磁数据进行稀疏化处理的效果，需要对稀疏化处理后的数据进行重构，通过重构性能指标来表明观测矩阵进行稀疏化处理的能力大小。大部分观测矩阵都是随机矩阵，也存在不足之处，因为在试验中具有不确定性，确定观测矩阵的性能需要大量实验以消除不确定性。高斯随机矩阵对大部分信号都满足不相关性，在稀疏采集的过程中需要的观测值要少一些，但是需要大量的计算和存储空间。主要选择的依据为感知性能、适用性、计算难度和硬件实现难度。

采用长度为N=256，取稀疏度为K=16的漏磁信号，选取观测值数量M=50，采用不同类型的观测矩阵，进行稀疏化处理，并用OMP算法进行数据重构，最终得到的不同观测矩阵的重构结果性能如表1所示。

从表1中可以看发现采用不同观测矩阵进行稀疏化处理时，得到的性能统计结果相差不是很大。其中，部分哈达玛矩阵的能量恢复系数最高，且均方误差很小。随机高斯矩阵的信噪比最高，在对漏磁数据进行稀疏化处理时，对噪声数据有一定滤过作用。

3 结语

本文详细介绍了压缩感知理论中的稀疏变换矩阵和观测矩阵，分析了漏磁数据的稀疏性并比较出适合的稀疏变换矩阵，设计了基于压缩感知的管道漏磁检测数据稀疏化方法。通过实验总结分析出这几种观测矩阵分别适用于带有不同特征的漏磁数据比较了其重构信号的准确程度，以便于更好地进行漏磁数据的稀疏化处理。

参考文献

[1] Ono S， Yamada I. A hierarchical convex optimization approach for high fidelity solution selection in image recovery[C]. Signal & Information Processing Association Summit and Conference. IEEE，2012：1-6.

[2] Zibulevsky M， Elad M. L1-L2 optimization in signal and image processing[J]. Signal Processing Magazine IEEE，2010，27（3）：76-88.

[3] 王强，张培林，王怀光.压缩感知中测量矩阵构造综述[J].计算机应用，2017，37（1）：188-196.

[4] 王金铭，叶时平，徐振宇，等.低存储化压缩感知[J].中国图象图形学报，2018，21（7）：835-844.