一类不确定混沌系统的驱动响应同步控制
2019-05-05范永青王敏娟
范永青, 刘 淳, 王敏娟
(西安邮电大学 自动化学院, 陕西 西安 710121)
近十几年来,驱动响应系统同步控制得到了国内外诸多学者们的关注,并取得了一系列重要的进展[1-2]。关于驱动响应系统同步的各种方法为解决实际问题提供了多种形式的应用,例如,对一类混沌系统的控制问题给出一种离散时间滑模控制方法[3]。对于带有时滞的Lur’e混沌系统的驱动响应同步控制问题,文献[4]基于线性矩阵不等式,提出一种采样数据控制器设计方法。文献[5]设计了量化采样控制器来保证驱动响应系统,从而实现全局指数渐进同步的方法。针对一类不确定驱动响应系统的同步问题,文献[6]给出了一种自适应鲁棒控制器设计方案。除此之外,还有其它多种形式的控制器设计方法[7-9]。尽管上述控制方法在解决驱动响应系统的同步问题中体现出了各自的特色与优点,但从控制器设计成本来看,状态反馈控制器具有设计简单、易于实现的优点[10]。因此,在实际应用中,状态反馈控制器一直受到了研究者的青睐。状态反馈控制器需要知道系统的全部信息,通常情况下,当被控系统中含有不确定项或者经常处于变化之中,而无法完全预先确定的情况,使得状态反馈控制在一定程度上受到限制。如何设计一个满意的控制器,使其能主动适应这些系统中未知或变化的特性情况,因此,根据系统中不确定项的信息来设计自适应控制是解决此类问题的关键[11]。
目前,自适应控制方法已经成为现代控制理论中的一个相当重要的一个分支,且发展最为迅速。自适应控制技术与其他多种控制方法的结合,为被控系统本身所具有的复杂性提供了有效的解决方法[11]。如模糊自适应控制[12]、自适应滑模控制[13]、自适应量化控制[14]等等。因此,针对不同被控对象本身特性,选择合适的自适应控制设计方案是值得探索的一个重要问题。
针对系统中的不确定项在满足Lipschitz条件的情况下,本文拟给出一种基于Lipschitz常数自适应反馈设计方法。该方法根据系统中不确定项的扰动边界信息,考虑系统的自适应状态反馈控制器,利用线性矩阵不等式设计状态反馈控制增益,并通过仿真例子进一步说明控制器的有效性。该方法与一般的纯反馈方法相比,不需要完全知道不确定项的所有信息,且设计方法简单,易于实现。
在本文中,对于对称矩阵X、Y,记号X>Y表示矩阵X-Y为正定矩阵。为简便表述,用符号“*”表示对称矩阵的转置,例如
1 问题描述与预备知识
考虑混沌驱动系统
x′(t)=A1x(t)+A2(x(t)),
(1)
其中,x(t)=[x1(t),x2(t),…,xn(t)]T为驱动系统的状态向量,矩阵A1,A2∈Rn×n为已知常数矩阵,非线性函数f(x(t))是满足Lipschitz条件的一个时变向量函数。
设响应系统为
y′(t)=(A1+ΔA1(r))y(t)+A2f(y(t))+
(B+ΔB(s))u(t)+Dw(q),
(2)
式中y(t)=[y1(t),y2(t),…,yn(t)]T为响应系统的状态向量,u(t)∈Rm×n为控制输入,常数矩阵B∈Rn×m,D∈Rn×m矩阵ΔA1(·),ΔB1(·)为不确定矩阵并满足不确定条件,向量函数w(q)∈Rn代表外界扰动。不确定参数(r,s,q)∈Ξ是Lebesgue可测的,其中Ξ代表紧致有界集。
若定义混沌同步误差为
e(t)=x(t)-y(t),
则由式(1)和(2)可知,误差系统的动态形式为
e′(t)=A1e(t)+ΔA1(r)x(t)+
A2[f(y(t))-f(x(t))]+
(B+ΔB(s))u(t)+DW(q)。
(3)
假设1存在适当维数的连续有界矩阵N1(·),N2(·)和M(·),使得不确定矩阵满足如下关系
ΔA1(r)=BN1(r),
ΔB(s)=BN2(s),
W(q)=BM(q),
(4)
其中,扰动项满足如下有界条件
(5)
假设2向量函数f(·)满足Lipschitz条件,即存在一个Lipschitz常数ε,对所有的x(t)∈Rn和y(t)∈Rn,满足条件
‖f(y(t))-f(x(t))‖≤ε‖y(t)-x(t)‖。
(6)
式中‖·‖表示欧氏范数。式(6)等价于不等式
[f(y(t))-f(x(t))]T[f(y(t))-f(x(t))]≤
ε2[y(t)-x(t)]T[y(t)-x(t)。
(7)

1)S<0;
是等价[15]的。

2 自适应控制器设计
设计自适应控制器的形式为
u(t)=Kαe(t)+uν,
(8)
其中
而
K为待设计的控制增益矩阵,矩阵P由下述定理1中求出正定矩阵,λmin(N2(s))表示矩阵N2(s)的极小值特征值,参数α的自适应律为

(9)
定理1如果假设1和假设2成立,则存在对称矩阵X>0,Q>0是正定矩阵和适当维数的矩阵Y,使得下面线性矩阵不等式成立
(10)
则在自适应控制器式(8)的控制作用下,混沌同步误差系统(3)可以实现同步。其中控制增益矩阵K=YX-1,P=X-1,ε和δ是给定的正常数。
下面将给出定理1的证明过程。选取Lyapounov函数为
(11)
在误差系统式(3)约束条件下,式(11)时间导数为

(12)
由控制器(9)可知,下列不等式成立。即

(13)
由(13)和控制器(8)和(9)可知,不等式(12)等价于

(14)
则由假设2知,可得不等式

(15)
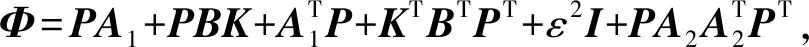
V′(t)≤ξT(t)Φξ(t)<0。
(16)
由(16)知,误差系统(3)是渐进稳定的,即满足

由Schur补引理1可知,式(16)等价于
(17)
在式(17)两边同时左乘以diag [P-1,I,I]和右乘以diag [P-1,I,I],并令P-1=X,KX=Y,线性矩阵不等式(10)成立,定理1证毕。
3 仿真算例
为了说明本文所设计的控制器,考虑如下驱动Chua’s 混沌系统
(18)
响应系统为
(19)
其中,f(x)=bx(t)+0.5(a-b)(|x(t)+1|-|x(t)-1|),系统中的参数为
a=-1.28,b=-0.69,
不确定项
不确定参数分别满足
|r|≤0.3, |s|≤0.5, |q|≤0.2。
由(19)可知,
N1(s)=[s2s3s],N2(s)=s,M(q)=q。
不确定参数选取为
r=0.3sin(t-1),
s=0.5cos(2t),
q=0.2cos(3t),
则它们的上界分别为
ρr=0.3,ρs=0.5,ρq=0.2。
驱动系统(17)的初始状态选为
x(0)=[0.8 0.1 0.1]T,
响应系统(19)的初值状态值为
y(0)=[0.9 -0.1 -0.3]T。
当不考虑控制的作用时,驱动系统和响应系统的同步误差时间响应曲线如图1所示。可见,同步始终存在误差。

图1 无控制作用下的同步误差时间响应
采用本文中设计的自适应控制器(8),使得驱动系统(18)和响应系统(19)达到同步,控制器中的参数为δ=0.0002,Lipschitz常数ε=0.05,通过解定理1线性矩阵不等式(10),得控制器增益矩阵
K=[4.0938 -43.6116 -5.3866],
正定矩阵

参数自适应律(9)的初始值为α(0)=0.03,相应的仿真误差曲线结果如图2所示,控制器中的自适应参数时间响应如图3。

图2 控制器作用下的同步误差时间响应

图3 控制器中的参数(9)时间响应
从仿真结果图2和图3可以看出,在自适应控制器(8)、(9)的控制作用下,驱动系统(18)和响应系统(19)可以在1秒内实现同步目的。
4 结语
针对在Lipschitz非线性条件下的一类不确定混沌系统的驱动响应系统同步问题,提出了一种利用LMI自适应控制方法。基于Lyapunov稳定性理论分析,使得驱动系统和响应系统的实现渐近同步。从仿真结果表明,本文方法所设计的控制器是有效可行的。
