河北 刘立涛

数学解题不仅是对数学知识本身的巩固与应用，在人的思维发展和严谨科学态度等方面的培养上也起着不可替代的作用，人们在对数学解题方法的探索上更是永无止境.那么，什么方法才是好的方法？什么方法才是高中生应该掌握的方法？怎样才能让他们掌握这些方法？这一系列中的每一个问题都够一个老师研究一辈子.笔者结合多年的教学经验，将几个较为典型的问题拿来和大家一起探究一下.

案例一——函数值域的求法

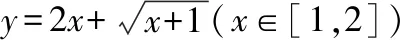
事实上，经观察，该函数是单调递增的，只需代入端点值即可.求值域问题一般来讲主要是两个方法：一、基本不等式法；二、函数单调性法.特别是函数单调性法主要研究两点：一、研究哪个函数的单调性？于是就产生了我们平常经常用到的“换元法”、“分离常数法”等，实质上这些方法都是对原函数进行值域上的等价变换.最终都是运用变换之后的函数的单调性来求值域的；二、如何研究单调性？于是就有了所谓“求导法”或者变换为“常用初等函数法”等，而研究函数的单调性，“肉眼观察法”才是基本功，才是第一方法.

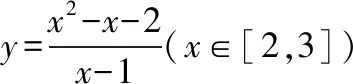
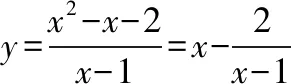
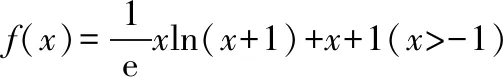
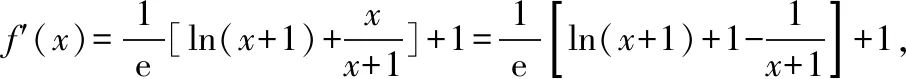
案例二——线性规划问题

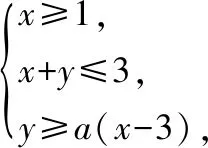
常规套路：1、将z=2x+y转化为y=-2x+z，利用z的截距意义进行讨论求解；

2、将2x+y理解成向量a=(2,1)与向量b=(x,y)的数量积.利用向量b=(x,y)在向量a=(2,1)上的投影的大小来解题.

事实上，“ax+by”作为一种运算形式，2x+y的最小值必然应该在可行域内寻找x，y都相对比较小的值，从图象可知即在该可行域内寻找最左下方的点，即为A点.通常的教学中，我们往往容易忽视这种代数和的最本源的运算意义和思想，无辜地走了一些弯路，也让学生钻到了解题的套路中.

( )

案例三——立体几何求解问题

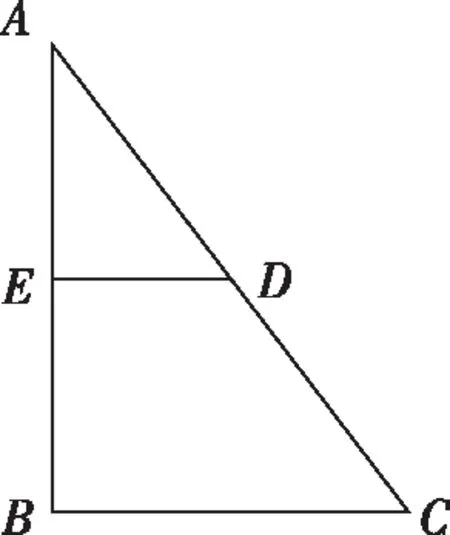
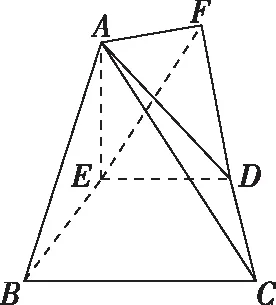
例题：直角三角形ABC中，AB=2BC=8，将△ABC沿着中位线DE折叠，得到如图所示的四棱锥A-BCDE,其中DA⊥DC.求平面ABE与平面ACD所成锐二面角的余弦值.

常规套路：建立空间直角坐标系，利用空间向量解题(方法略).

事实上，将BE和DC进行延长相交于点F，连接AF.在△ABF中，因为EF=AE=BE，所以∠FAB=90°，同理可证，∠FAC=90°，根据二面角的平面角的定义，易知，∠BAC即为平面ABE与平面ACD所成锐二面角的平面角.空间想象和直观想象一直是考试大纲要求的核心能力和素养，能够通过直观判断找到二面角的平面角会相应减少空间向量的运算量.求角问题中的补形与找角往往可以使问题的解答更直观和简单.

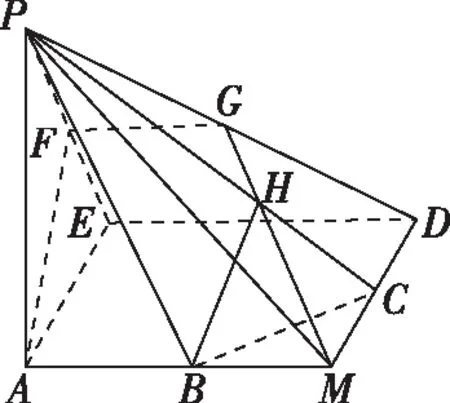
练习：如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点，在五棱锥P-ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H.若PA⊥底面ABCDE，且PA=AE，求直线BC与平面ABF所成角的大小，并求线段PH的长.

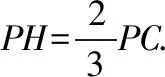
案例四——解析几何计算面积问题

解析几何中的运算相对繁琐，我们不提倡利用诸如“圆锥曲线硬解定理”之类的方法和方式增加学生的记忆负担.但是，如果对有些内容和知识的推理上再精进一步，往往会让运算变得相对简单一些.

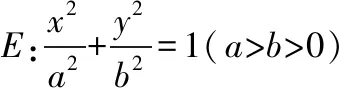
(Ⅰ)求E的方程；

(Ⅱ)设过点A的动直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程.

案例五——解三角形的平面几何知识的应用

解三角形问题本质上就是解决三角形的问题，属于平面几何范畴.所以，在解决解三角形问题的时候，如果能结合图象特征和几何性质往往会有效地减少运算量.

例题：在△ABC中，D，E是BC边上两点，BD，BA，BC构成以2为公比的等比数列，BD=6，∠AEB=2∠BAD，AE=9，则三角形ADE的面积为

( )

A．31.2 B．32.4

C．33.6 D．34.8

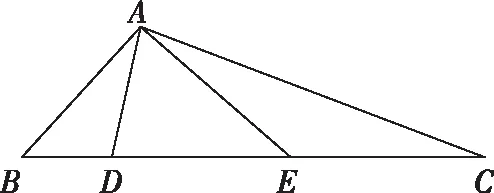
通常解法：正弦余弦定理(解法略)解法繁琐

( )

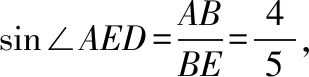
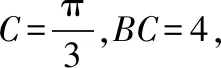
解法点拨：取AC的中点F，连接EF，解三角形EFD即可求出∠EDF.而∠EDF与∠A互余.

后记：