山东 王中华

核心素养着力培养的是提高学生面对复杂情境问题的解决能力，使之能够适应飞速发展的信息时代和复杂多变的未来社会.学生发展核心素养，主要指学生应具备的，能够适应终身发展和社会发展需要的必备品格和关键能力.逐步学会用数学的眼光观察世界，发展数学抽象、直观想象素养；用数学的思维分析世界，发展逻辑推理、数学运算素养；用数学的语言表达世界，发展数学建模、数据分析素养．增强创新意识和数学应用意识．本文通过具体的例子探讨六大数学核心素养在不等式、函数与导数中的渗透.

素养一、数学抽象

样题1.若对于定义在R上的函数f(x)，其图象是连续不断的，且存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数都成立，则称f(x)是一个“λ伴随函数”.下列是关于“λ伴随函数”的结论：

( )

A.1 B.2

C.3 D.4

【素养在线】本题考查“新定义”，解题的关键是正确理解“新定义”，并用“新定义”解决问题，主要是能将“新问题”转化为“老问题”、用“老方法”解决问题.此类题型是高考的一个亮点,是用数学符号、文字叙述给出一个教材之外的新定义，如本题中的“λ伴随函数”，要求考生在短时间内通过阅读、理解后，抽象出“λ伴随函数”的实质，解决题目给出的问题.解决该类问题的关键是准确把握新定义的含义，对新定义提炼升华，把从定义和题目中获取的信息进行有效整合，并转化为熟悉的知识加以解决,以此考查学生数学抽象素养．

( )

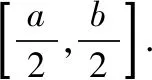
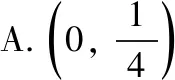
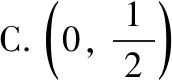
【解析】因为函数f(x)=log2(2x+t)为“倍缩函数”，定义域D={x|2x+t>0},

易知f(x)在[a,b]上是增函数，

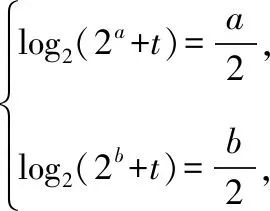
素养二、逻辑推理

样题2．(2018·全国卷Ⅱ理·21)已知函数f(x)=ex-ax2．

(1)若a=1，证明：当x≥0时，f(x)≥1；

(2)若f(x)在(0,+∞)只有一个零点，求a．

【解析】(1)证明：当a=1时，f(x)≥1等价于(x2+1)·e-x-1≤0．

设函数g(x)=(x2+1)e-x-1，则g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x．

g′(x)≤0，所以g(x)在(0,+∞)单调递减．

而g(0)=0，故当x≥0时，g(x)≤0，即f(x)≥1．

(2)设函数h(x)=1-ax2e-x．

f(x)在(0,+∞)只有一个零点等价于h(x)在(0,+∞)只有一个零点．

(i)当a≤0时，h(x)>0，h(x)没有零点；

(ii)当a>0时，h′(x)=ax(x-2)e-x．

当x∈(0,2)时，h′(x)<0；当x∈(2,+∞)时，h′(x)>0．

所以h(x)在(0,2)单调递减，在(2,+∞)单调递增．

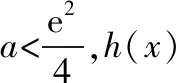
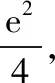
故h(x)在(2,4a)有一个零点，因此h(x)在(0,+∞)有两个零点．

【素养在线】逻辑推理包括归纳推理和演绎推理. 演绎推理是从一般性的前提出发，通过推导，即“演绎”，得出具体陈述或个别结论的过程.演绎推理的逻辑形式对于理性的重要意义在于它对人的思维保持严密性、一贯性有着不可替代的校正作用.演绎推理的最典型、最重要的应用，通常存在于逻辑和数学证明中. 本题运用了演绎推理,需要先构造函数g(x)=(x2+1)e-x-1，再求导函数，根据导函数不大于零得函数单调递减，最后根据单调性证得不等式.研究f(x)的零点，先利用导数确定只有一个零点的必要条件，再利用零点存在性定理确定条件的充分性，即得参数a的值.

【变式训练2】(2018·全国卷Ⅲ理·21)已知函数f(x)=(2+x+ax2)·ln(1+x)-2x．

(1)若a=0，证明：当-10时，f(x)>0；

(2)若x=0是f(x)的极大值点，求a．

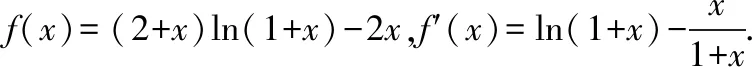
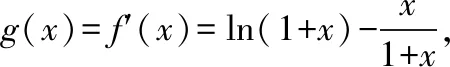
当-10时，g′(x)>0.故当x>-1时，g(x)≥g(0)=0，当且仅当x=0时，g(x)=0，从而f′(x)≥0，当且仅当x=0时，f′(x)=0.

所以f(x)在(-1,+∞)单调递增.

又f(0)=0，故当-10时，f(x)>0.

(2)(i)若a≥0，由(1)知，当x>0时，f(x)≥(2+x)·ln(1+x)-2x>0=f(0)，这与x=0是f(x)的极大值点矛盾.

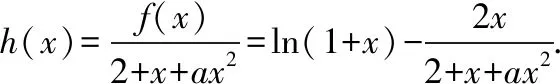
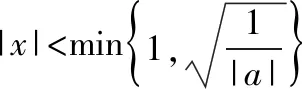
又h(0)=f(0)=0，故x=0是f(x)的极大值点，当且仅当x=0是h(x)的极大值点.

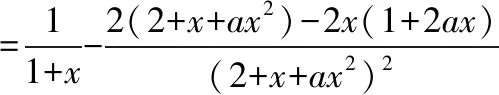
故x=0不是h(x)的极大值点.

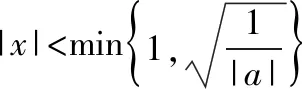
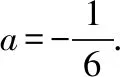
素养三、数学建模

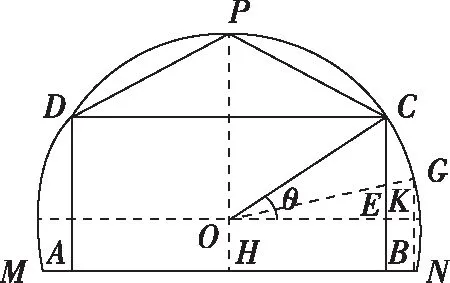
样题3．(2018·江苏卷·17)某农场有一块农田，如图所示，它的边界由圆O的一段圆弧MPN(P为此圆弧的中点)和线段MN构成．已知圆O的半径为40米，点P到MN的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD，大棚Ⅱ内的地块形状为△CDP，要求A,B均在线段MN上，C,D均在圆弧上．设OC与MN所成的角为θ．

(1)用θ分别表示矩形ABCD和△CDP的面积，并确定sinθ的取值范围；

(2)若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4∶3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．

【解析】(1) 连接PO并延长交MN于H,则PH⊥MN,所以OH=10.过O作OE⊥BC于E,则OE//MN,所以∠COE=θ,故OE=40cosθ,EC=40sinθ,

则矩形ABCD的面积:S矩形ABCD=(40sinθ+10)×80cosθ=800(4sinθcosθ+cosθ)，

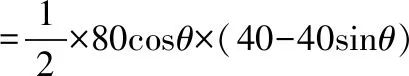
=1 600cosθ-1 600sinθcosθ.

过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.

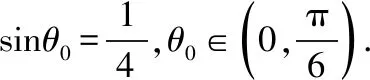
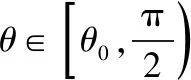
(2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3．

设甲种蔬菜的单位面积年产值为4k(k>0),则乙种蔬菜的单位面积年产值为3k,设年总产值为y.

f′(θ)=cos2θ-sin2θ-sinθ=-2sin2θ-sinθ+1=-(2sinθ-1)(sinθ+1).

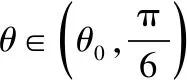
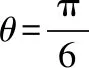
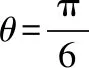
【素养在线】本题需要建立矩形ABCD和△CDP的面积关于θ的三角函数模型, 建立甲、乙两种蔬菜的年总产值关于θ的三角函数模型,然后利用导数研究函数的单调性求最值.以此考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.利用数学建模解决实际应用问题，首先要正确理解题意，分析条件和结论，理顺数量关系，选择恰当的模型；其次，将文字语言、图形(或数表)等转化为数学语言，利用数学知识建立相应的数学模型，将实际问题化为数学问题，选择合适的数学方法求解，再利用数学知识如函数、导数、不等式等解决问题；最后将利用数学知识和方法得出的结论，还原为实际问题的答案．在求解过程中要注意实际问题对变量参数的限制条件．

【变式训练3】如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.则十字形的最大面积是________.

【解析】设S为十字形的面积,则

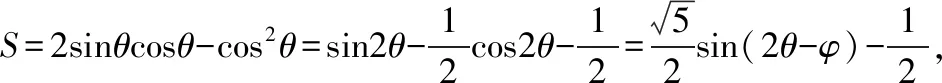
素养四、数学运算

( )

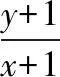
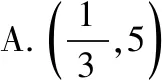
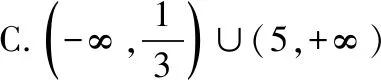
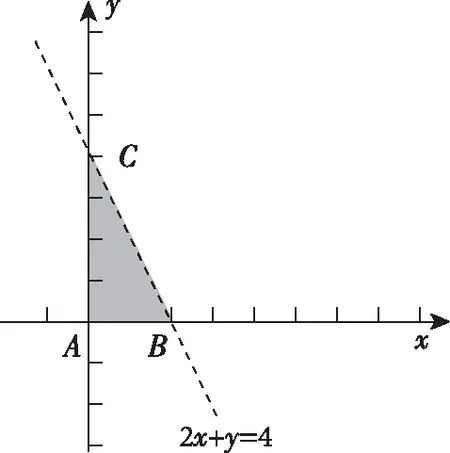
【素养在线】数学运算是学生必备的最基本的数学素养,只有具备了成熟的数学运算素养,才能走出“会而不对，对而不全”的困境.数学运算包括对数字的计算、估值和近似值计算，对式子的组合变形与分解变形，对几何图形和几何量的计算求解等. 运算的准确、合理和熟练是数学能力高低的重要标志，需要经过反复训练才能提高这种能力,本题属于线性规划中的斜率型最值问题.【另解】中的“估算”简单快捷. 对于客观题，合理的估算往往比盲目的精确计算和严谨推理更为有效.

【解析】画出不等式组表示的可行域(如图中阴影部分所示)．

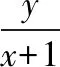
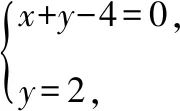
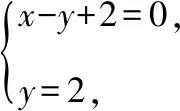
素养五、直观想象

( )

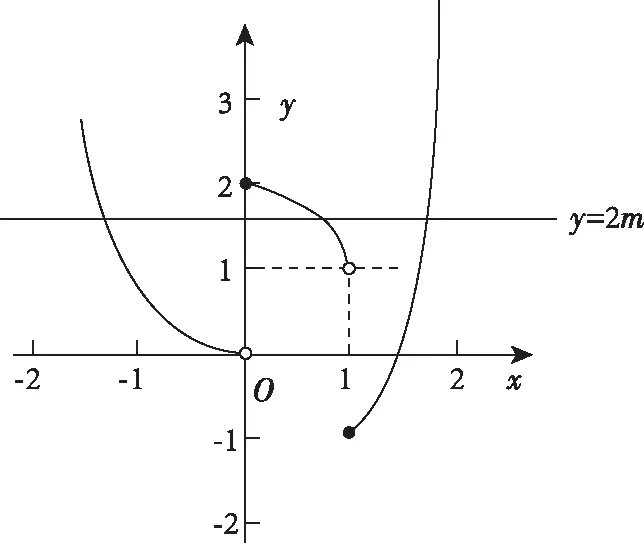
【解析】当x<0时,g(x)=-x+1>0,此时g(g(x))=(-x+1)2-1=x2-2x；

当0≤x<1时,g(x)=x2-1<0,此时g(g(x))=-(x2-1)+1=-x2+2；

当x≥1时,g(x)=x2-1≥0,此时g(g(x))=(x2-1)2-1=x4-2x2,

作出函数y=g(g(x))和y=2m的图象如下：

素养六、数据分析

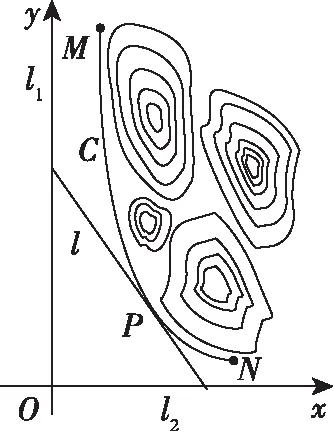
(1)求a，b的值；

(2)设公路l与曲线C相切于P点，P的横坐标为t．

①请写出公路l长度的函数解析式f(t)，并写出其定义域；

②当t为何值时，公路l的长度最短？求出最短长度．

【解析】(1)由题意知,点M,N的坐标分别为(5,40), (20,2.5).

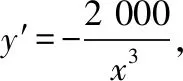
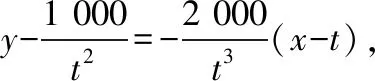
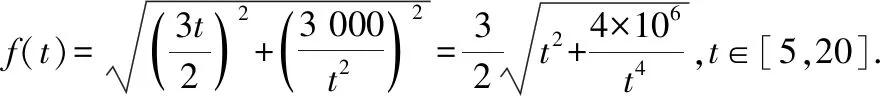
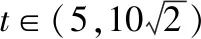
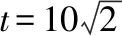
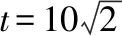
【变式训练6】 为了美化城市，某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，如图所示．要求B在AM上，D在AN上，且对角线MN过C点，|AB|=3米，|AD|=2米．

(1)要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？

(2)若AN的长度不小于6米，则当AM，AN的长度是多少时，矩形AMPN的面积最小？并求最小面积．

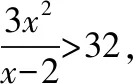
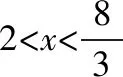
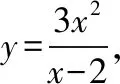
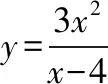
此时|AN|=6米，|AM|=4.5米．