改进复调制的频率校正算法研究
2019-04-08岛新煜李超旺
岛新煜,高 敏,李超旺
(1.陆军工程大学石家庄校区导弹工程系,河北 石家庄 050000;2.陆军工程大学石家庄校区弹药工程系,河北 石家庄 050000)
0 引言
快速傅里叶变换(fast Fourier transform,FFT)作为一种经典的频谱分析,常被用来处理动态信号[1]。然而,由FFT获得的离散频谱在频率测量过程中会产生较大的误差,不能够满足工程实际的要求。为了弥补由FFT算法在测频精度上造成的误差,一些研究工作者长期致力于相关理论的研究并取得了一些成果[2-6]。复调制算法(zoom-FFT,ZFFT),由于其原理简单及物理概念清晰,已经被广泛地应用于实际工程中[7]。然而,ZFFT在应用过程依然存在以下两点不足:一方面,由于存储空间的限制,对于频谱不可能无限放大;另一方面,栅栏效应仍然对频率估计的精确性造成影响。为此,本文在ZFFT的基础上,提出一种利用牛顿插值的校正方法,以避免栅栏效应的影响,从而提高测频精度。
1 ZFFT算法的基本原理
ZFFT算法的核心是对输入信号进行复调制。复调制后的信号再通过低通滤波器、重采样、FFT和频率调整获得最终的调制信号[8]。ZFFT原理如图1所示。

图1 ZFFT原理图Fig.1 Schematic diagram of ZFFT
假定输入信号为x(n),经复调制后得到:
(1)
式中:f0和fs分别为输入信号的中心频率和采样率。
相应的频谱关系为:
Y(ejω)=X[j(ω+2πf0)]
(2)

(3)
经过FFT变换后,得到:
(4)
因此,由式(4)可以看出,经ZFFT处理后,原始频谱被放大了M倍。
2 本文所提频率估计算法
大部分的目标信息通常包含在信号频谱的峰值位置,因此对信号频谱峰值位置对应的频率进行估计是本文研究的重点。为实现精确估计,将频率估计步骤分为粗估计和精估计两步。然而,即使ZFFT相较于FFT提高了频谱的分辨率,在估计频率与真实频率之间依然存在偏差δ。因此,此处将ZFFT视为粗估计,要实现精确估计,还需对频率进行进一步校正。
牛顿插值作为一种有效的函数近似方法,可以根据选取的函数点对原函数进行有效拟合。牛顿插值的各阶插值之间有递推关系,当增加节点时计算十分方便。假设已知x0,x1,…,xn和相应的函数值yi=f(xi)(i=0,1,…,n),则近似函数[9-10]表示为:
Nn(x)=f(x0)+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+…+f[x0,x1,…,xn](x-x0)×
(x-x1)…(x-xn-1)
(5)
式中:f[x0,x1,…,xn]为差商。
(6)
当n≥2时,
(7)

理论上,选取的函数点越多,获得的函数越精确,但计算的复杂度及所需的计算时间便会显著增加。考虑到经ZFFT后的离散频谱及与目标频率的相关点数,分别以三点插值和四点插值为例来说明本文频率校正的方法。FFT和ZFFT频谱如图2所示

图2 FFT和ZFFT频谱图Fig.2 Spectrum of FFT and ZFFT
2.1 三点拟合校正
假设频谱峰值位置及其相邻两点的位置分别为k0、k0-1、k0+1,相应的幅值分别为Y(k0)、Y(k0-1)、Y(k0+1),则相应的牛顿插值函数可以表示为:
Nn(k)=Y(k0-1)+f[k0-1,k0][k-(k0-1)]+
f[k0-1,k0,k0+1][k-(k0-1)](k-k0)
(8)
f[k0-1,k0]=Y(k0)-Y(k0-1)
(9)

(10)
为了得到峰值位置处的频率,需要对牛顿插值函数Nn(k)进行微分,即:

(2k-2k0+1)
(11)

(12)
式中:kp为对峰值位置的估计。
估计频率表示为:
(13)

2.2 四点拟合校正
在三点拟合校正(three power factor couection,3PFC)的基础上,只增加一个函数点[(k0-2,Y(k0-2)]或[k0+2,Y(k0+2)],形成四点拟合校正(four power factor couection,4PFC)。这里,我们选择点[k0-2,Y(k0-2)]来说明。
牛顿插值函数可以表示为:
Nn(k)=Y(k0-2)+f[k0-2,k0-1][k-(k0)]+f[k0-2,k0-1,k0][k-(k0-2)][k-(k0-1)]+f[k0-2,k0-1,k0,k0+1][k-(k0-2)][k-(k0-1)](k-k0)
(14)
f[k0-2,k0-1]=Y(k0-1)-Y(k0-2)
(15)
(16)
(17)
令a=f[k0-2,k0-1]、b=f[k0-2,k0-1,k0]、c=f[k0-2,k0-1,k0,k0+1],并计算Nn(k)的极值,得到:
(18)

(19)
(20)
由式(16)和式(17),可以得到:

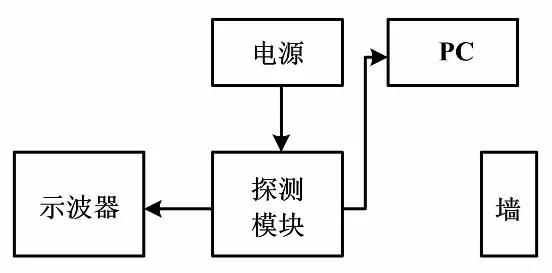
通过前面的叙述可以明显发现,Y(k0)>Y(k0-1)>Y(k0-2)以及Y(k0)>Y(k0+1),因此,b+3c<0,c<0,故可以得到kp1 (21) 在前面的叙述中,介绍了ZFFT算法和本文所提的频率校正方法。为了检验上述方法的校正效果,通过数值试验进行验证。首先,考察上述方法在不同频率下的频率估计精度并计算各自的误差,频率范围为1.6~6.4 MHz,步长为0.4 MHz。之后,检验各方法在噪声条件下的表现。最后,分析在误差范围内,不同偏离程度δ对估计精度的影响。输入的余弦信号幅值设为1,采样数N为1 024,采样率设定为15 MHz以满足奈奎斯特采样定理。 以某雷达测距系统为背景,选择中心频率为1.6~6.4 MHz(步长为0.4 MHz)的输入信号进行试验。 不同算法的频率估计及相应误差如表1所示。 与ZFFT相比,所提算法的频率估计精度明显有所提升,通过表中数据可以发现,本文所提方法的频率估计误差平均减少了30%。 表1 不同算法的频率估计及相应误差Tab.1 Frequency estimation and corresponding errors with different algorithm 在实际的测试环境中,信号不可避免地会受到噪声的干扰。噪声的影响往往会降低估计的精度,同时使得频率估计具有随机性。鉴于此,在输入信号上加上零均值的高斯白噪声来检验所提方法对噪声的灵敏性。噪声的大小可以用信噪比(signal noise ratio,SNR)来衡量。假定SNR从0~20 dB以步长为1 dB变化,在每一个信噪比下进行1 000次蒙特卡洛仿真,观察频率估计效果,并与克拉美罗下限作对比。RMSE的克拉美罗下限表示为[10]: (22) ρ表示SNR,因为N≫1,所以均方根误差的克拉美罗下限可以简化为: (23) 不同SNR的均方根误差曲线如图3所示。 图3 不同SNR的均方根误差曲线Fig.3 RMSE curves with different SNR 由图3可以看出,SNR越高,频率估计的表现越好。这也反映了在实际情况中,信噪比越高,噪声对信号的影响就越小,频率的估计精度也会越高。与ZFFT相比,文中所提方法的均方根误差明显更接近克拉美罗下限,说明其误差更小,在噪声环境下的表现优于ZFFT。随着信噪比的减小,ZFFT算法估计的平方根误差逐渐呈指数形式增长,这意味着在低信噪比条件下,ZFFT算法已经不能很好地进行频率校正。但是,在这种情况下,3PFC或4PFC算法依然能够保持一定的优势。 在前面的叙述中,偏差δ反映了估计频率与真实频率之间的偏离程度,其受采样频率的限制。这里,考虑不同的偏差对频率估计造成的影响。图4表示不同偏差(δ=0.1、0.2、0.3、0.4)下均方根误差随SNR的变化曲线。由于ZFFT的误差较3PFC和4PFC过大,ZFFT的误差曲线不再在图中标出。 由图4可以发现,当SNR低于5 dB时,噪声是影响误差的主要因素;而当SNR大于5 dB时,偏差则是影响估计精度的主要因素。随着偏差的增大,频率估计的均方根误差也会随之逐渐增大。当偏差较小时,3PFC的校正效果要优于4PFC;而当偏差较大时,4PFC的校正效果则好一些。 为验证算法在实际定距下的效果,基于调频连续波系统,设计了定距试验。试验测试原理图如图5所示。所选用的探测模块原理如图6所示。 图4 不同偏差下的均方根误差曲线Fig.4 RMSE curves with different deviation 图5 测试原理图Fig.5 Schematic diagram of the test 图6 探测模块原理图Fig.6 Structure diagram of the detection module 载波频率设置为24.5 GHz,频偏为2 MHz,发射功率为8 mW。探测模块与墙之间的距离分别设定为2 m、3 m、4 m、5 m、6 m、7 m、8 m 。将探测模块预先放在设定的距离处,通过计算机观察输出的距离值,结果如表2所示。可以发现,相比ZFFT,本文所提的算法在测距精度上均有所提升。 表2 距离测试结果Tab.2 Results of range test 本文提出了一种基于牛顿插值的频率校正方法,能够使频率估计更加精确。理论上分析了传统复调制算法的特点,并推导了本文所提算法的校正公式。本文方法的原理易于理解,保持了较低的计算成本。在应用复调制算法时,不需要设置较大的频谱放大倍数,节省了数据存储空间。另外,讨论了白噪声和偏差对估计精度的影响。试验结果表明,相比于ZFFT,本文所提方法具有良好的噪声适应性,这也为今后满足更高要求的频率估计奠定了基础。
3 仿真校验
3.1 不同方法的精度比较

3.2 噪声影响

3.3 偏差影响
3.4 实际定距验证



4 结束语
