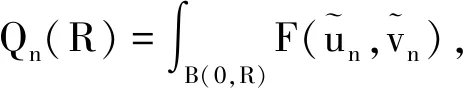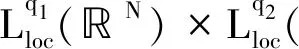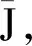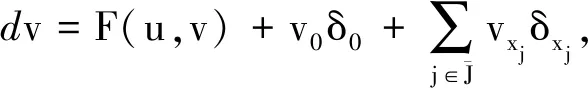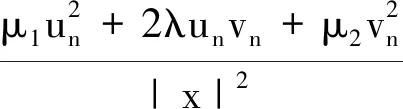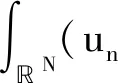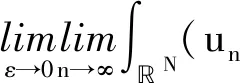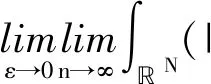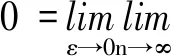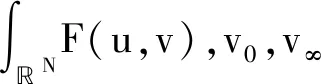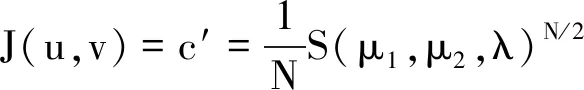康东升，刘梦茹，高蒙

(中南民族大学 数学与统计学学院,武汉 430074)

1 相关知识

本文研究如下带有多重强耦合Hardy项的临界椭圆方程组：

(1)

其中参数满足下列条件：

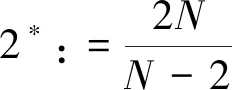
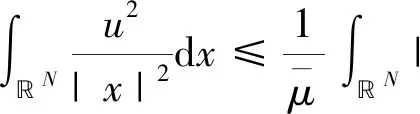
D1,2(N)是N)关于范数的完备化空间.

自从2001年Bose-Einstein凝聚理论被证实以后，有关Bose-Einstein凝聚的研究便是国际物理学界研究的热门领域之一，研究者们为Bose-Einstein凝聚建立了相应的数学物理方程组，如下所示：

(2)

可以看出方程组(2)是如下方程组的一种特殊情况：

(3)

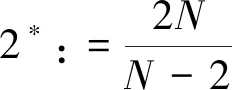
(4)

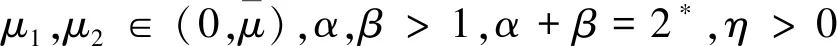
(5)

这里Ω是N中的一个有界光滑域.作者指出当时方程组(5)不存在正解.

受到方程组(4)与(5)的启发，本文研究临界椭圆方程组(1)的基态解，它带有方程组(4)中的非耦合Hardy项和方程组(5)中的强耦合Hardy项以及多重Sobolev临界项.该方程组目前还没有被其他人研究过，是一个全新的问题. 从数学角度出发，方程组(4)其实就是方程组(1)中λ=0的一种特殊情况，当λ≠0时，方程组(1)中的耦合Hardy项使方程组变得更加复杂，增大了研究难度.本文我们主要研究λ>0时方程组(1)的基态解.

γ1(u2+v2)≤μ1u2+2λuv+μ2v2≤γ2(u2+v2),

其中γ1,γ2是矩阵A的特征值.记D:=D1,2(N)，由Hardy，Sobolev和Young不等式，可以定义如下最佳Sobolev常数：

(6)

方程组(1)对应的能量泛函为：

|v|2*)dx,

其中J∈C1(D×D,).对于(u,v)∈D×D{(0,0)},若

J′(u,v),(φ,φ)=0,∀(φ,φ)∈D×D,

则称(u,v)是方程组(1)的一个解，这里J′(u,v)是J在(u,v)的Fréchet导数.设(u0,v0)∈D2{(0,0)}是方程组(1)的解，并且对于方程组(1)的任意一个解(u,v)∈D2{(0,0)}都有J(u0,v0)≤J(u,v)，则称(u0,v0)为方程组(1)的基态解.

定义极小能量：

这里

通过直接计算可以得到[4]：

(7)

η|u|α|v|β,

则有：

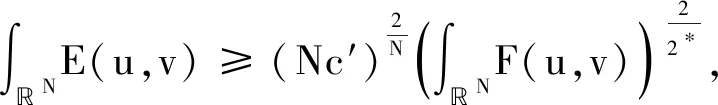
本文的主要结果可以归纳为以下定理：

在本文中,为了书写方便用C来表示常数，有时也会省略积分式中的dx.

2 定理1的证明

本部分证明方程组(1)基态解的存在性.

定理1的证明令(u*,v*)为(u,v)∈′的Schwartz对称化，其中u,v≥0，根据文献[5]可得：

再由Pólya-Szegö不等式可得：

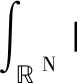
由上可得：

存在0

定义：

通过直接计算，可以得到(un,vn)∈′,J(un,vn)→c′,且un,vn≥0为径向对称的递减函数，由伸缩变换的不变性知：

(8)

(9)

由上式可得{(un,vn)}在D2上有界. 故存在子列{(un,vn)}⊂D2，使得：

(un,vn)⇀(u,v)，在D2中，

(un,vn)→(u,v)，a.e.在N上，

(10)

(11)

(12)

其中δx表示在点x的Dirac质量.为了讨论在无穷远处的集中性[8]，我们记：

(13)

(14)

(15)

则有：

(16)

因为xj∈N{0}，则由(10)～(12)式有：

(17)

(18)

(19)

(20)

通过(17)～(20)式得：

(21)

再由(6)式可得：

(22)

根据不等式(21)和(22)可推出命题1成立.

命题2 v0=0或v0≥(S(μ1,μ2,λ))N/2.

(23)

(24)

(25)

(26)

根据(23)～(26)式得：

(27)

由(6)式得：

(28)

则根据(27)和(28)式可推出命题2成立.

命题3 v∞=0或v∞≥(S(μ1,μ2,λ))N/2.

命题3的证明类似于命题2，这里略去.

综上所述，得到：

(29)

由(10)～(16)式以及(29)式可以得到：

S(μ1,μ2,λ)·

(30)

再由(8)和(9)式，可以得到：

与假设矛盾，所以得到vxj=0. 同理可证得v0=0,

综上所述，可知{(un,vn)}在D2{(0,0)}中强收敛到(u,v)，使得J(u,v)=c′并且

所以(u,v)≠(0,0),u≥0,v≥0.利用拉格朗日乘数法可以得到J′(u,v)=0，(u,v)为方程组(1)的非负径向对称严格递减的基态解.

定理1证明完毕.