孙兆永 贾 晗 杨 军

(1中国科学院噪声与振动重点实验室(声学研究所) 北京 100190)

(2中国科学院大学 北京 100049)

0 引言

Mikaelian透镜是一种具有柱对称折射率的自聚焦器件[1]，其折射率在宽度方向呈现出关于中心轴对称的反双曲余弦分布。由于它有着良好的自聚焦能力，因此在成像及信息传递方面有着极其重要的应用价值。二维Mikaelian透镜是矩形的，它的参数分布规律确定，因此利用近些年发展起来的梯度折射率超材料就可以很容易地实现。在某些场景下，需要在聚焦的同时令波的传播路径发生一定的偏转，普通的Mikaelian透镜显然无法满足需求。如何设计出一款集自聚焦与波束偏转两功能于一身的声学器件是一个研究热点。近些年发展起来的变换理论为此提供了一种实现的可能性[2−4]。变换声学理论通过坐标变换的方法将器件的声学参数与空间变换紧密地联系起来，并被广泛地应用于声学隐身[5]、声学偏转装置[6−7]等声学器件的设计。本文提出了利用共形变换理论设计声学器件的一般方法，并利用指数映射设计出了弧形的Mikaelian透镜，解析地分析了所设计弧形透镜的参数分布规律。仿真结果显示，该透镜在产生自聚焦效应的同时能够很好地令声波偏转一定的角度。

1 共形变换在超材料器件设计中的应用

共形变换是指一个曲面到另一个曲面之间能够保持微小区域相似性的映射，在理论物理及工程应用方面有着重要的用途[8]，而在变换声学中，它为设计二维及三维轴对称各向同性声学器件提供了方便简洁的参数求解方法。由于共形变换通常用复变函数描述更方便，因此在这里将用复空间进行讨论。本节主要讨论基于共形变换的二维声学器件设计方法，三维轴对称器件可以利用将二维器件绕主轴旋转的方法实现，而普通的三维器件无法用共形变换实现。图1展示了共形变换声学的过程，Ω空间和Ω′空间分别为已知参数分布的声学器件和待定参数的声学器件。在两个声学器件空间中建立映射关系便可利用声波方程的协变性得到两器件的参数关系。设背景空间，Ω空间和Ω′空间的密度和模量分别为ρ0和K0，ρz和Kz，ρω和Kω，Ω空间和Ω′空间相对背景介质的折射率分别为nz和nω。由于背景介质在后文中不详细讨论，因此其坐标系在这里不给予详细描述。Ω空间和Ω′空间的坐标系分别为z=x+iy和ω=u+iv。则在三个空间中的声波方程分别为

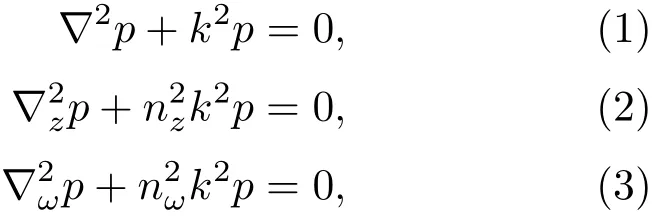
其中，∇、∇z和∇ω分别为三个空间的坐标系所对应的导数算子，k是声波在背景介质中的波矢。为了方便起见，分别称空间Ω和空间Ω′为虚空间和物理空间。假设虚空间的声学参量为已知，则利用声波方程的协变性，通过映射ω=ω(z)可以求得虚空间和物理空间的折射率之间满足[3]

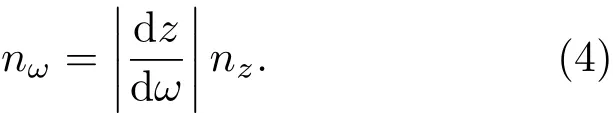
方程(4)建立了虚空间和物理空间之间的联系，通过求解此方程便可得到物理空间的折射率分布，从而求出其声学参量。需要指出的是，方程(4)等号右边分别与映射关系ω=ω(z)和虚空间参数相关。因此，声学器件的参数分布共同取决于虚空间参数分布和具体的映射关系。相同的虚空间，不同的映射可能得到不同参数分布的声学器件；同理，相同的映射，不同的虚空间也会得到不同参数分布的器件。

为了设计出弧形Mikaelian透镜，首先需要了解普通Mikaelian透镜的声学特性。然后在此基础上，利用方程(4)得到弧形Mikaelian透镜的折射率分布。

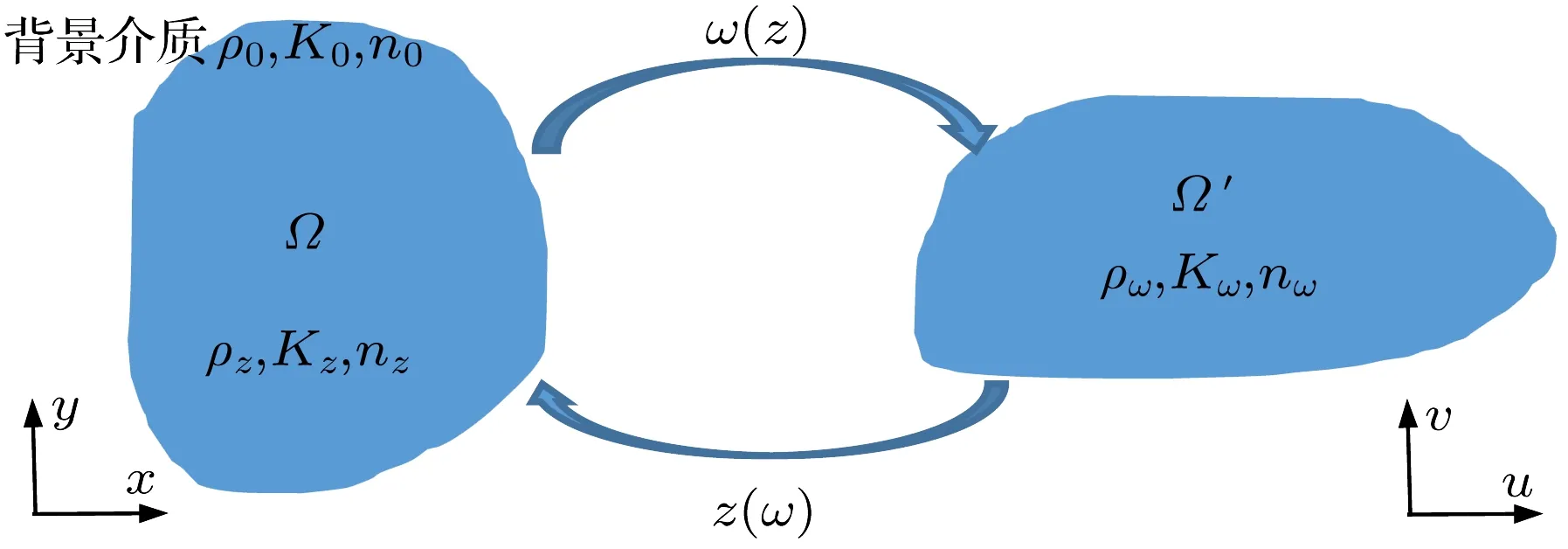
图1 共形变换声学示意图Fig.1 A schematic diagram of conformal transformation acoustics

2 普通Mikaelian透镜的自聚焦效应

Mikaelian透镜是由A.L.Mikaelian在1951年设计的一种自聚焦柱对称介质。这种介质的折射率nr从边缘到中心轴成反双曲余弦增加，可表达如下[1]：

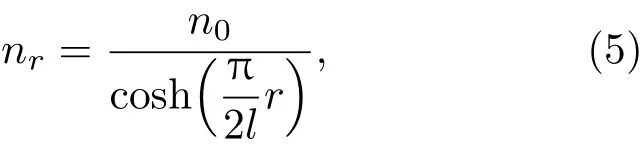
其中，r是到中心轴的距离，l是透镜的焦距，n0是透镜在中心轴的折射率。二维Mikaelian透镜是矩形的，形状如图2(a)所示，其折射率可以写为

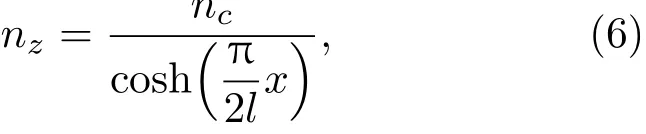
其中，x为到中心轴的距离，nc是透镜中心轴处的折射率，l为透镜的焦距。

为了能使该透镜在水下使用，需使其与水阻抗匹配。若设水的密度为ρ0、模量为K0，则其声速为，透镜的密度记为ρz，模量记为Kz，则声速。阻抗匹配的水下透镜的密度与声速满足：

继而可得

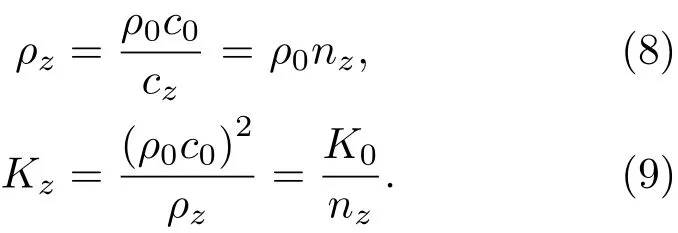
从公式(8)和公式(9)可知，密度与折射率成正比，模量与折射率成反比。在本文中透镜的参数为宽度d=0.216 m，焦距为l=0.4 m，长度为L=4l，即透镜长度包含一个周期，如图2(a)所示。透镜中心处相对于水的折射率为nc=1.5，则透镜的折射率分布nz(r)如图2(d)所示。可以看到Mikaelian透镜的折射率确实成中心轴对称分布，在中心轴处折射率达到最大，而随着偏离中心呈反双曲余弦减小的趋势，在边缘处折射率达到1.38的最小值。对透镜的密度和模量进行归一化，则归一化的模量和密度分布如图2(b)和图2(c)所示，模量在轴心处达到最小，而密度在轴心处达到最大。这与公式(8)和公式(9)所描述的一致。

Mikaelian透镜对入射声波的聚焦效应如图3(a)所示。入射声波为160 kHz的高斯脉冲。在透镜中，波束进行了两次聚焦，焦斑分别在y=l和y=3l处。图3(b)反映了在y=l和y=2l处沿着透镜宽度方向声压的幅值分布。波束在y=l处声波能量主要集中在离中心轴约0.02 m的狭窄区域内，这表明透镜有着良好的聚焦能力。在y=2l处声波能量较平缓的分布在离中心轴约0.08 m的区域内，波束恢复到入射波的形状。

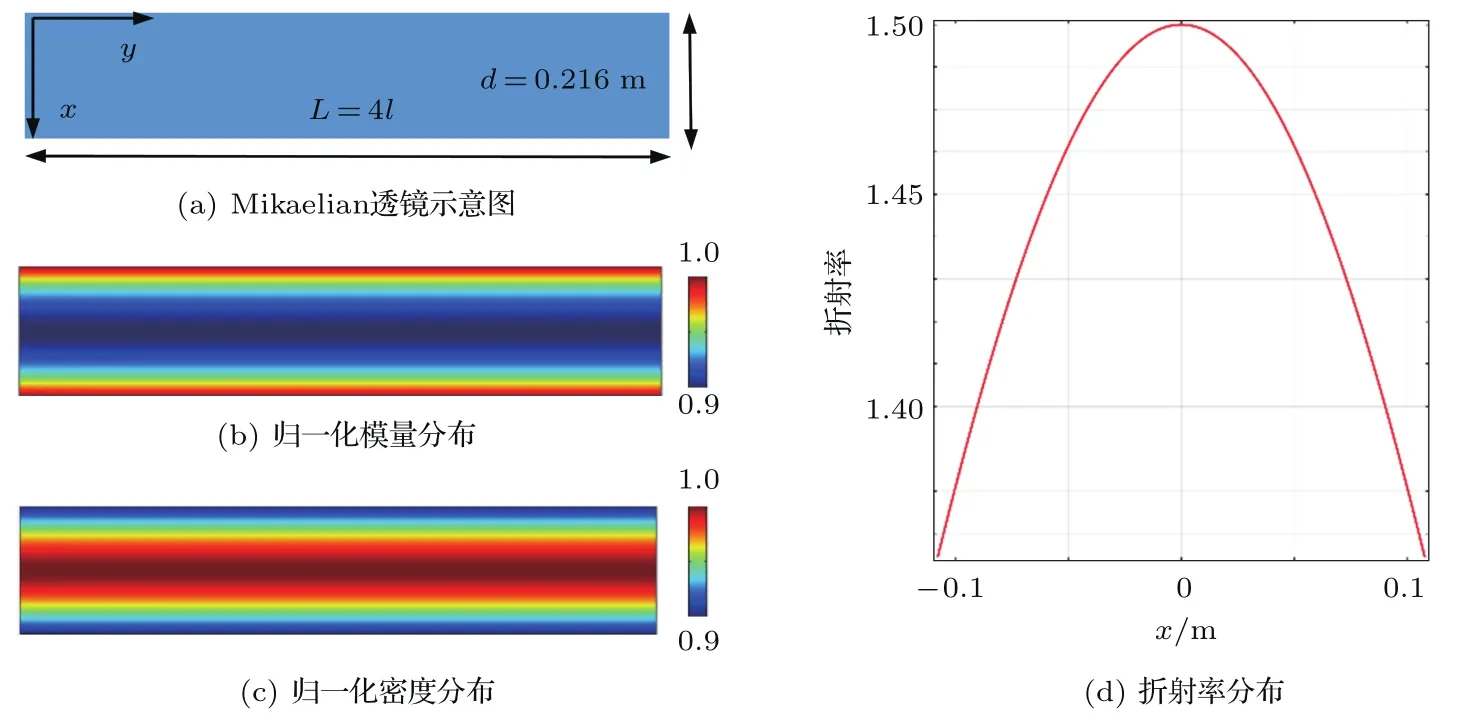
图2 Mikaelian透镜及其声学参数分布Fig.2 A sketch map of Mikaelian lens and the distributions of the parameters

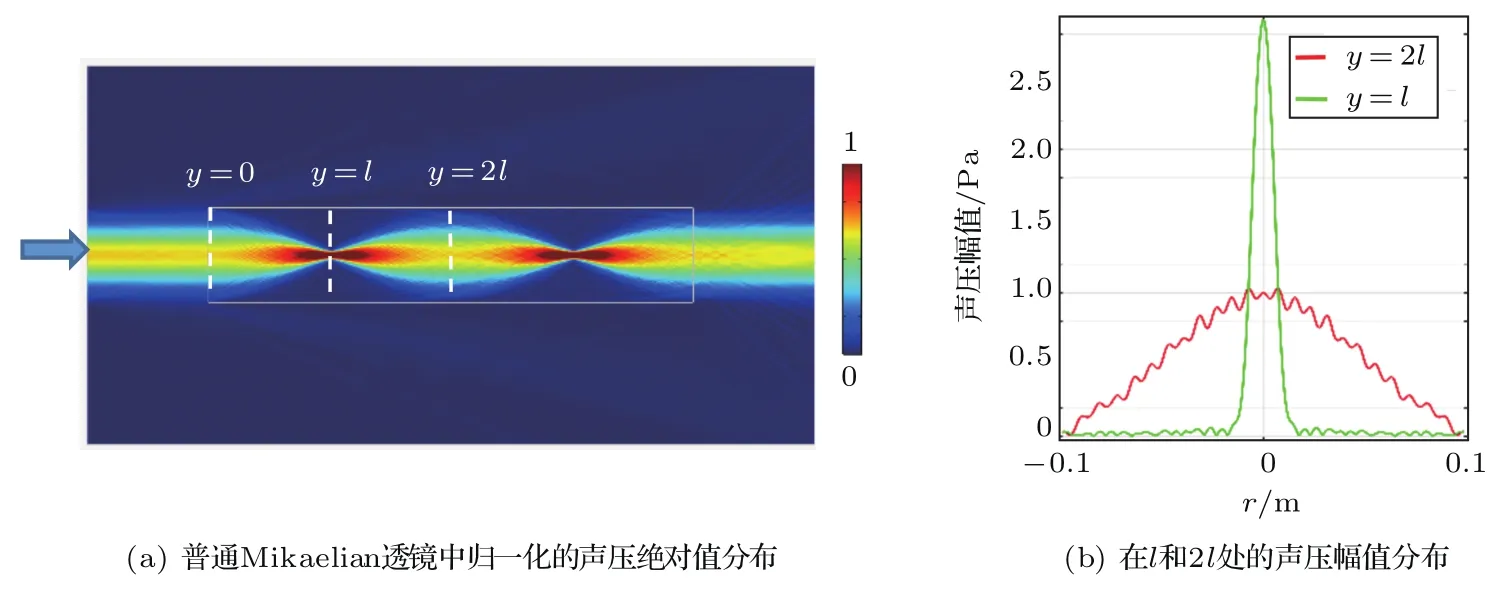
图3 Mikaelian透镜内的声场分布Fig.3 The distribution of the acoustic pressure in the Mikaelian lens

以上是对普通Mikaelian声透镜聚焦效应的分析。根据第1节的理论，可以利用共形映射在普通Mikaelian透镜的基础上设计出弧形的自聚焦透镜。

3 基于指数映射的弧形Mikaelian透镜设计

根据第1节的分析，将普通Mikaelian透镜看做虚空间，通过共形变换可以实现弧形Mikaelian透镜的设计。在共形变换中，指数映射可以将一个矩形区域映射到一个环形区域，因此为设计弧形透镜提供了思路。该设计的变换过程如图4所示。

图4 指数映射将Mikaelian透镜映射成弧形Fig.4 From ordinary Mikaelian lens to curved Mikaelian lens by exponential mapping

普通Mikaelian透镜的空间用复坐标z=x+iy表示，而弧形透镜的空间用ω=u+iv=reiθ表示。通过共形映射ω=ω(z)将z空间的普通Mikaelian透镜映射到ω空间，从而得到共形Mikaelian透镜的参数分布。根据第2节的理论，只要知道了z空间到ω空间的具体映射关系即可得到其参数分布。为了计算的简洁，设映射关系为

其逆映射为

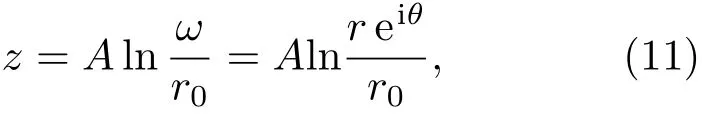
其中，r0和A都是常数，它们决定了共形透镜的内外半径和圆心角ϕ。由方程(4)和方程(6)可得共形透镜的折射率分布为

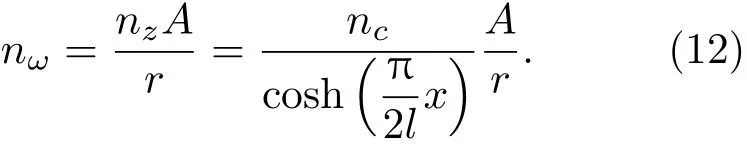
考虑到z=Aln(ω/r0)，因此，x=Aln(r/r0)，y=Aθ，则方程(12)可写为

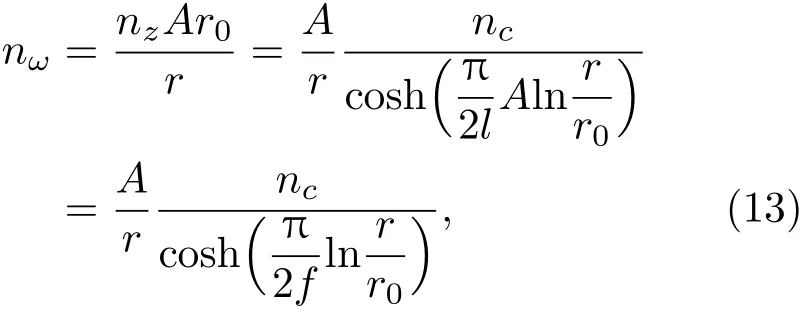
这里ϕ=l/A是弧形透镜焦点所在的角度，由参数A与原透镜焦距共同决定。根据前文分析，则共形透镜的密度和模量分别为

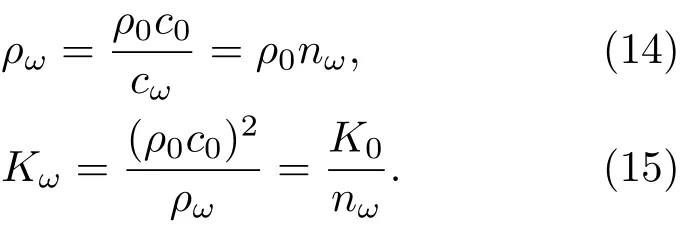
取A=r0=0.5 m，则带入可得r1=0.40 m，r2=0.61 m，弧形透镜焦点所在角度ϕ=0.80 rad，如图5(a)所示，透镜的圆心角为θ0=4ϕ。弧形Mikaelian透镜沿径向的折射率分布如图5(b)所示，可以看到，与普通Mikaelian透镜不同的是，弧形Mikaelian透镜的折射率约在rf=0.495 m而非宽度的中心rc=(r2−r1)/2=0.505 m处达到最大，折射率并不成对称分布，这也与公式(13)所描述的相吻合。这是由指数映射本身的不对称性决定的，透镜焦点的位置与映射的参数关系较密切，调节指数映射的参数A和r0可以使焦点的位置发生改变，但同时也会改变透镜的折射率分布。根据公式(14)和公式(15)即可得到相应的密度和模量分布。弧形Mikaelian透镜归一化的模量和密度分布如图5(c)和图5(d)所示。模量和密度均呈现出角向对称的分布模式，而在径向方向，模量在rf=0.495 m处达到最小，在两端呈增加趋势，在外径处达到最大；而密度的分布恰与模量相反，与公式(14)和公式(15)比较一致。

需要指出的是，利用共形变换所设计的弧形透镜是各向同性的，而弧形透镜的实现并不唯一地取决于共形映射，其他映射也可以实现，但映射的选取会影响到透镜参数的分布。

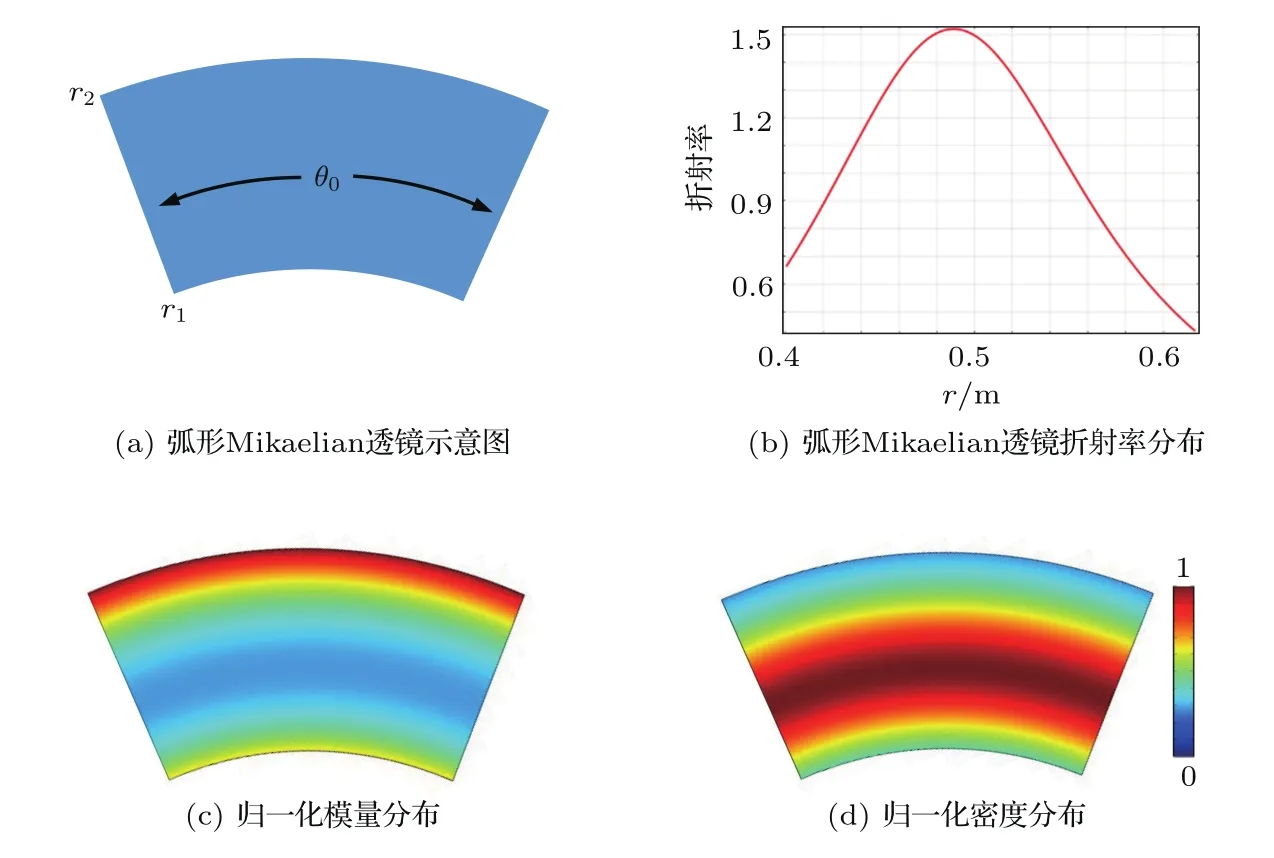
图5 弧形Mikaelian透镜及其参数分布Fig.5 A sketch map of curved Mikaelian lens and the distributions of the acoustic parameters

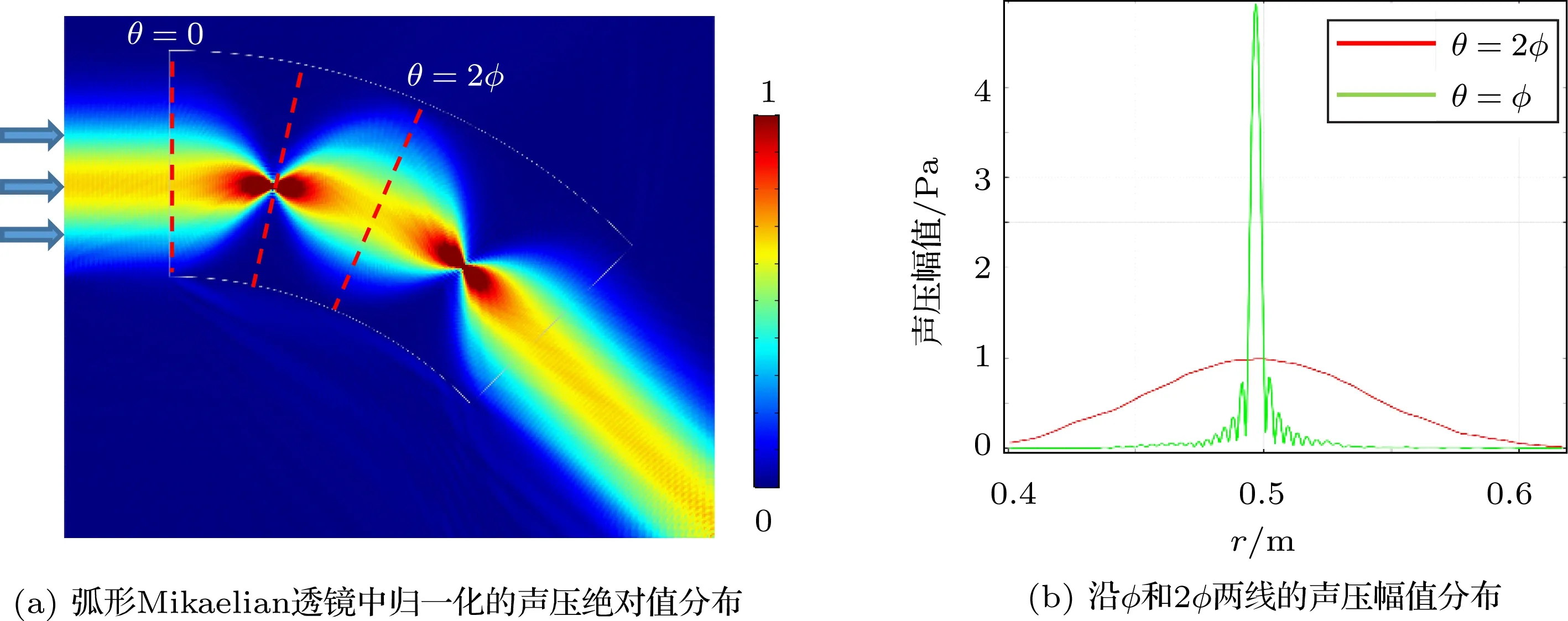
图6 弧形Mikaelian透镜的声场分布Fig.6 The distribution of acoustic pressure of the curved Mikaelian lens

为了验证所设计共形透镜的声学效果，对其进行数值仿真模拟。仿真过程在商业有限元软件COMSOL Multiphysics中进行。共形透镜的背景介质为水，如图6(a)所示，频率为 160 kHz中心声压为1 Pa的高斯束从y=0.495 m处向右入射，分别在θ=ϕ和θ=3ϕ处各聚焦一次，并在θ=2ϕ和θ=4ϕ处成像。在θ=ϕ和θ=2ϕ处提取其声压幅值，则声压幅值的分布如图6(b)所示。在θ=2ϕ处，声压在rf达到最大，值为1 Pa，并随着偏离rf而缓慢减小；而在θ=ϕ处，声压也在rf处达到最大，且最大值达到θ=2ϕ处最大值的4.5倍左右，并且随着r偏离rf，声压急剧下降，分别在r=0.48 m和r=0.52 m处减小到约0.1 Pa。这表明了在焦点位置声波的能量主要聚集在0.48∼0.52 m区域内，也说明了弧形Mikaelian透镜极好的聚焦能力。这与仅能改变波束传播方向的普通弧形声波波导完全不同[9]。与普通Mikaelian透镜一样，通过共形变换所得的弧形透镜内也包含一个周期，即共形透镜的周期为θ=4ϕ。

对比图6和图3可以看到，弧形的Mikaelian透镜表现出了与普通Mikaelian透镜类似的自聚焦声学效应，在焦距的奇数倍处，声波会汇聚于一点，而在偶数倍焦距处，波束恢复到入射波的特征。在聚焦的同时，也可以看到声波通过弧形透镜时传播方向偏转了θ0的角度。

4 结论

本文分析了利用共形变换设计声学器件的一般方法，并指出通过共形变换可以计算出器件的声学参数与虚空间声学参数之间的关系。在此基础上，将普通Mikaelian透镜当作虚空间，利用指数映射设计出了弧形的Mikaelian透镜。与普通Mikaelian透镜不同的是，由于指数映射的不对称性，弧形Mikaelian透镜的折射率分布并不是完全对称的，而是在内径处较小，在外径处最小，在内外径中点偏向内径的地方达到最大。通过有限元仿真验证了弧形透镜不仅拥有与普通透镜类似的聚焦效应，还能够在聚焦的同时令声波发生偏转。在工程应用中，可以利用超材料，如五模材料，实现弧形透镜的设计，设计过程与声波弯管的设计过程类似[6−7,9]。该理论为实现弧形声学器件提供了理论支持和设计方案。