达选尚, 杨 刚

(兰州交通大学 数理学院, 甘肃 兰州 730070)

1 引言与预备知识

20世纪60年代后期,在交换的Noether环上,Auslander等[1]推广了有限生成投射模的概念,引入了G-维数为0的模(简称G-模).1995年,Enochs等[2]将G-模的概念进行了推广,在任意结合环上,引入了Gorenstein投射模的概念.此后,Gorenstein投射模受到了国内外许多学者的关注(参见文献[3-5]及其相关文献).2009年,文献[6]引入了一类特殊的Gorenstein投射模,即强Gorenstein平坦模.后来,Gillespie[7]将这类模称为Ding投射模.目前已有许多学者对Ding投射模进行了广泛的研究[8-12].

环与模的扩张问题是环与模范畴研究中的基本问题之一.在环扩张下,可以从一个环上的模获得另一个环上的模结构.Frobenius扩张作为一种特殊的环扩张,首先是由Kasch[13]引入的.后来,Morita[14]和Nakayama等[15]对Frobenius扩张进行了深入研究.在这种环扩张下,文献[16]研究了模的Gorenstein投射性的保持性质.受此启发,本文主要讨论Frobenius扩张环上模的Ding投射性质.为后文需要,下面介绍一些已知概念.

全文中R总是指有单位元1(≠0)的结合环,所有模均指酉R-模.除非特别声明,本文中的R-模均指左R-模.

定义1.1[16]称环扩张R⊂A是Frobenius扩张,如果以下等价条件中的任意一条成立:

1) 函子A⊗R-和HomR(A,-)是自然等价的;

2)RA是有限生成投射模,且AAR≅(RAA)*=HomR(RAA,R);

3)AR是有限生成投射模,且RAA≅(AAR)*=HomRop(AAR,R);

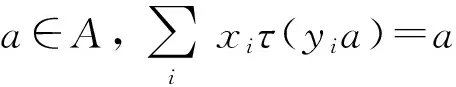
以下关于Frobenius扩张的例子参见文献[17].

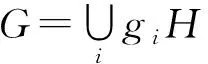
2) 设F是一个域,A=M4[F]是F上的矩阵代数.设R是A的子代数,且R的F-基是如下幂等元和矩阵单位

e1=e11+e44,e2=e22+e33,

e21,e31,e41,e42,e43,

则R⊂A是可分的Frobenius扩张.

定义1.3[7]称R-模M是Ding投射模,如果存在R-模的正合序列

→P-2→P-1→P0→P1→,

使得每个Pi是投射R-模,M≅Ker(P0→P1),并且对任意平坦R-模F,函子HomR(-,F)作用该正合序列后仍然得到正合序列.

2 Frobenius扩张环上的Ding投射模

文献[16]研究了Frobenius扩张环R⊂A上模的Gorenstein投射性质,证明了若左A-模M是Gorenstein投射模,则左R-模M是Gorenstein投射模.特别地,若R⊂A是Gorenstein Frobenius扩张,则一个左A模M是Gorenstein投射模当且仅当M是Gorenstein投射R-模.下面将研究Frobenius扩张环上模的Ding投射性质.

为了方便,首先给出以下引理.

引理2.1设R⊂A是Frobenius环扩张,P是左A-模.如果P是投射A-模,那么P是投射R-模.

证明因为A是投射R-模,所以对于R-模的正合序列

0→K→L→N→0,

存在正合序列

0→HomR(A,K)→HomR(A,L)→

HomR(A,N)→0.

又由于P是投射A-模,所以序列

0→HomA(P,HomR(A,K))→

HomA(P,HomR(A,L))→

HomA(P,HomR(A,N))→0

正合.又因为对于任意A-模M,有A⊗AM≅M.由伴随同构定理知存在如下交换图:

易得上面交换图中的第三行正合,从而P是投射R-模.

引理2.2设环扩张R⊂A是Frobenius扩张,M是左A-模,则如果M是Ding投射A-模,那么M是Ding投射R-模.

证明设M是Ding投射A-模,则存在正合序列

η:=→P-1→P0→P1→,

其中每个Pi是投射A-模,M≅Ker(P0→P1),并且对任意平坦A-模G,HomA(η,G)是正合序列.由引理2.1知每个Pi是投射R-模.设F是平坦R-模.由于环扩R⊂A是Frobenius扩张,HomR(A,F)≅A⊗RF.显然A⊗RF是平坦A-模,因此HomR(A,F)是平坦A-模.从而序列HomA(η,HomR(A,F))正合.另一方面

HomA(η,HomR(A,F))≅

HomR(A⊗Aη,F)≅HomR(η,F),

所以序列HomR(η,F)正合.因此,M是Ding投射R-模.

引理2.3设R⊂A是环扩张,P是左A-模.如果P是投射R-模,那么A⊗RP是投射A-模.

证明对于A-模的正合列

0→K→L→N→0,

存在以下正合列

0→HomA(A,K)→HomA(A,L)→

HomA(A,N)→0.

由于P是投射R-模,所以以下序列正合

0→HomR(P,HomA(A,K))→

HomR(P,HomA(A,L))→

HomR(P,HomA(A,N))→0.

又由伴随同构定理易得下面序列也正合

0→HomA(A⊗RP,K)→HomA(A⊗RP,L)→

HomA(A⊗RP,N)→0.

故A⊗RP是投射A-模.

引理2.4设环扩张R⊂A是Frobenius扩张.如果F是平坦A-模,那么F是平坦R-模.

证明对于右R-模的正合列

0→M→N→L→0,

有以下正合列

0→M⊗RA→N⊗RA→L⊗RA→0.

另一方面有交换图：

由于F是平坦A-模,所以上图中的第一行正合,从而第三行也正合,由此得到F是平坦R-模.

定义2.5[16]称环扩张R⊂A是可分扩张,如果乘法映射φ:A⊗RA→A(a⊗Rb→ab)是可裂满的A-双模同态.称环扩张R⊂A是可分的Frobenius扩张,如果R⊂A既是Frobenius扩张,又是可分扩张.

定义2.6[16]以下条件等价:

1) 环扩张R⊂A是可分扩张;

2) 对每个A-双模M,θ:A⊗RM→M是A-双模的可裂满态射;

3) 存在元素e∈A⊗RA,使得φ(e)=1A且对任意a∈A,ae=ea.

定理2.7设环扩张R⊂A是可分的Frobenius扩张,M是左A-模,则M是Ding投射A-模当且仅当M是Ding投射R-模.

证明必要性 由引理2.2可得,下面证明充分性.

由M是Ding投射R-模知,存在正合列

η:=→P-1→P0→P1→,

其中每个Pi是投射R-模,M≅Ker(P0→P1),并且对任意平坦R-模Q,HomR(η,Q)是正合序列.由引理2.3知A⊗RPi是投射A-模.另外,对于任意的平坦A-模F,

HomA(A⊗Rη,F)≅HomR(η,HomA(A,F))≅

HomR(η,F).

又由引理2.4知F是平坦R-模,所以HomR(η,F)是正合序列,从而序列HomA(A⊗Rη,F)正合.显然A⊗Rη是正合序列,且

A⊗RM≅Ker(A⊗RP0→A⊗RP1).

故A⊗RM是Ding投射A-模.因为环扩张R⊂A是可分扩张,所以由定义2.6知A-模M是A⊗RM的直和项.又由文献[9]中的推论2.7知，Ding投射模的类对直和项封闭,故M是Ding投射A-模.

由定理2.7容易得到如下结论.

推论2.8设环扩张R⊂A是可分的Frobenius扩张,M是左A-模,则以下条件等价:

1)M是Ding投射A-模;

2)A⊗RM是Ding投射A-模;

3)M是Ding投射R-模.

设M是左R-模.令Dpd(M)=inf{n|存在左R-模的正合列0→Gn→→G0→M→0,其中每个Gi是Ding投射模},则称Dpd(M)是M的Ding投射维数.如果没有这样的n存在,那么Dpd(M)=∞.关于Ding投射维数的研究可以参考文献[6,10-12].

命题2.9设环扩张R⊂A是可分的Frobenius扩张,M是左A-模,且M具有有限的Ding投射维数,则DpdR(M)=DpdA(M).

证明不妨设DpdA(M)=n,则存在左A-模的正合序列

η:=0→Gn→Gn-1→→G0→M→0,

其中每个Gi是Ding投射A-模.由引理2.2知每个Gi也是Ding投射R-模.从而DpdR≤n,即DpdR(M)≤DpdA(M).

另一方面,若DpdR(M)=n,则存在左R-模的正合序列

ξ:=0→Dn→Dn-1→→D0→M→0,

其中每个Di是Ding投射R-模.从而有正合序列A⊗Rξ:

0→A⊗RDn→A⊗RDn-1→

→A⊗RD0→A⊗RM→0.

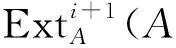
综上可得DpdR(M)=DpdA(M).