张安珍 李建中

摘要：很多领域产生的大量数据都可以很自然地用不确定图模型表示和描述，如蛋白质交互网络、社交网络、无线传感器网络等。本文研究不确定图上最可靠的最小生成树问题，该问题具有广泛的应用价值和研究意义。精确地求解算法需要枚举所有可能的最小生成树并找出其中出现次数最多的那个。因此，枚举开销随着边数增多呈指数增长，当图规模较大时并不可行。为此本文提出了一个时间复杂度为O（d |V|²）的启发式贪心算法，其中d为最大的顶点度数，|V|为顶点数。实验结果表明，该算法具有较好的效率和较高扩展性。

关键词：不确定图：最可靠最小生成树：贪心算法

0引言

近年来，很多领域产生的大量数据可以利用图模型表示。由于测量数据的工具不精确、数据本身性质等多方面原因导致图数据普遍存在不确定性，如蛋白质交互网络（PPI）、社交网络、无线传感器网络等，将不确定性融入到图中得到不确定图。

确定图上的最小生成树问题具有十分重要的实际意义。在连通图G=（v.E）中，E中每条边有对应的权值，图G的一棵生成树是连接V中所有顶点的一棵树，生成树中所有边的权值总和称为生成树的代价，使这个代价最小的生成树称为图G的最小生成树（Minimum Spanning Tree.MST）。很多实际应用问题可以通过求解最小生成树得到很好的解决。例如，道路规划问题，可将各个城镇作为图的顶点，城镇之间的道路作为边，每条道路的修建代价作为边上的权值，在该图上求最小生成树可以得到修建代价最少的修路方案。如，在无线传感器网络中，由于传感器节点间的通信链路存在一定的干扰，每条链路存在一定的失效风险，因此其拓扑结构可以很自然地建模为不确定图。顶点表示各传感器节点，边表示可能存在的通信链路，边的权值由距离决定，边的存在概率表示该链路正常工作的可能性大小。在该图上求解最可靠的最小生成树非常重要，其上的边集即链路集合是最稳定可靠的连通路径，利用该生成树可以优化路由选路过程，用最少的代价完成全部节点间通信的同时，保证了网络通信的可靠性与稳定性。

不确定图是边带有概率的特殊加权图，边的概率表示该边存在的可能性大小。因此不确定图有多种可能的存在形式，每一个存在形式称为蕴含子图，蕴含子图是一个以一定概率确定存在的加权图，由此可知每个连通的蕴含子图上都有至少一棵最小生成树，这些最小生成树构成了不确定图的最小生成树集合。

本文研究不确定图上最可靠的最小生成树问

1问题定义

本节介绍一种不确定图模型，并形式化描述不确定图上的最可靠的最小生成树问题。

1.1不确定图模型

不确定图是一个四元组G=（v.e.p.W），其中V是顶点集，E为边集，P是边的存在概率函数，即E到（0.1]的映射，P（e）表示边e存在的概率，W为权重函数，定义了每条边的权值大小。由于边的不确定性导致不确定图具有多种存在形式，每种确定的存在形式称之为蕴含子图，也称为可能世界。所有的蕴含子图构成不确定图所蕴含的确定图集合，记为Imp（G）。对于g∈Imp（G），称之为G蕴含g.记作C→g.假定所有边相互独立，蕴含概率P（G→g）等于所有g中的边的存在概率与不在g中的边不存在概率之积，如公式（1）所示。

下面通过一个简单的例子来说明蕴含子图及其存在概率的含义。

例1如图1（a）所示，图G是包含3个顶点和3条边的不确定图，每条边存在与否决定了图G共有2³=8个蕴含子图，每个子图的存在概率由公式（1）计算得到。以图1（b）中的子图g²为例，P（C→g²）=0.4×（1-0.9）×（1-0.7）=0.012.其它子图的存在概率计算与之类似，结果如图1（b）所示。

1.2 最可靠的最小生成树

下面通过例2求图1（a）中不确定图G上的MST_max来说明公式（3）的含义。

MST_max是最小生成树集合中存在概率最大的那棵，即MST₃，MST_max={Ac，BC}，P（MST_max）=P（MST₃）=0.378，利用|MST|表示最小生成树的代价，则|MST_max|=|MST₃|=7。

由MST_max的定義可知，一种直观的求解算法是枚举所有蕴含子图g.并在g上求最小生成树得到一个最小生成树集合，求集合中存在概率最大的最小生成树，然而该算法在实践上并不可行，图G共有2^|E|，个蕴含子图，枚举代价随边数增多呈指数增长，当图规模较大时，算法效率十分不理想。因此本文提出一种启发式的贪心算法近似求解MST_max，时间复杂度为0（d²|V|²），相对于枚举法性能大大提高，实验结果表明该算法在通常情况下能够得到MST_max。

2贪心算法求最可靠最小生成树

启发式贪心策略近似求解不确定图上最可靠的最小生成树，在2.1节给出算法的详细描述，而后在

2.2节分析贪心算法的运行时间。

2.1 算法描述

给定连通不确定图G=（v.e.p.W），求解其上MST_max的算法思想与Prim算法求解确定图上最小生成树类似，维持一棵树a.树A从任意根顶点r开始形成，并逐渐生成，直至树A覆盖了V中的所有顶点，每一次，一条连接树A与G_A=（v.A）中某孤立顶点的概率最大的轻边被加入到树A中，其中轻边是指权值最小的边，下面给出概率最大轻边的定义。

定义1概率最大的轻边（Light Edge withMaximum Probability.LEMP），将所有连接树A与森林G_A=（v.A）中某孤立顶点的边加入队列S中，按公式（4）计算其加入到树A中的概率，其中概率值最大的边即为LEMP。

将队列S中的边按权值非降序排列，p_i表示位于排序队列中第i条边的存在概率，l≤i≤|S|，则第i条边作为概率最大的轻边（LEMP）加入到树A中的概率P;为：

其中，n_i表示队列中所有与第i条边权值相等，但位置排在其前面的边的个数，O≤n;≤i-1。下面举例说明公式（4）。

例3假设G中所有与A中顶点直接相连但不在A中的边有{e₁，e₂，e₃}，将其加人队列s.按照权值升序排列，假设w₁2=w₃，则这3条边加入到树A中的概率依次为：P₁，（1-P₁）·P₂，（1-P₁）·P₃。

直观地讲，e₁具有最小权重值w₁，故其作为轻边加入树A的概率就是其自身的存在概率p₁;对于e₂，由于其的权值w₂大于e₁的权值w₁，，所以只有在e₁不存在的情况下，e₂才能作为轻边加入到A中，概率为e₁不存在的概率乘以e₂存在的概率，即（1-p₁）·p₂;对于e₃，由于e₃的权值w₃和e₂的权值w₂，相等，则其加入到A的概率与e₂存在与否无关，概率等于e₁不存在的概率乘以e₃存在的概率，即（1-p₁） ·p₃。

下面给出具体的算法描述，见算法1。实现时，采用插入排序法排序队列s.因为每次添加新边之前，S中已有的边是按权值升序排列的，只需要将新加入的边插入到已经排好序的队列中即可，这样减少了全部边重新排序的时间开销。

算法1最可靠的最小生成树算法，

输入：不确定图G=（v.e.p.W）。

输出：最可靠的最小生成树MST_max的边集A

（1）MST_V={r};A=φ;S=φ

（2）将所有与r相连的边添加到队列S中

（3）WHILE|MST_V|<|V|DO

（4）将S中的边按照权值升序排列

（5）按照公式（4）计算S中每条边加入A的概率值

（6）利用最大堆H求概率最大的边，记为（u.v）

（7）将（u.v）加入A中，将不在MST_V中的顶点

（8）假设是v.加入到MST_V中

（9）删除S中所有与v相连的边

（10）将G中所有与v相连但另一端的顶点不在MST_V中的边加入到S中

（11）END WHILE

2.2算法的分析

下面分析最坏情况下算法的运行时间。将图G中最大顶点度数记作d.1≤d≤|V-1|，第i次迭代时队列S₁的长度记为|S₂|则有如下关系成立：

第一次迭代时，A中只有一个顶点r.将r的邻边加入到S₁中，最多加入d条边;第i+1次迭代时，S_i+1中的边由S_i去掉包含新顶点v的边后，再并上G中v的邻边中另外一端不在A中的边，其中S_i最少去掉

3实验验证

3.1实验环境及实验数据

为了验证启发式贪心算法的效率以及有效性，分别在合成数据集和人造数据集上进行测试。采用C^{编程，实验环境为PC机，英特尔（R）酷睿2双核2.4GHz CPU和2GB的主内存，运行系统为Ubutu 12.04。MapReduce算法在完全分布式环境下测试，Hadoop版本为2.6.0.实验环境为3台PC机，配置为英特尔（R）酷睿TM四核3.4GHz CPU和32GB内存。}

实验中的合成数据集是在真实不确定图数据上，随机标注权值得到，权值取0-100之间的整数。使用文献[6]提供的2个真实的不确定图数据集，Nature是蛋白质交互网络，Flickr是一个社交网络，图规模及连通性见表1.其中N（MST）表示MSF_max中包含的连通分支数目。

人造数据集采用随机生成一些不确定图，顶点之间的边及边上的权值和概率都随机生成，权值取O-100之间的整数，概率取值0.00-0.99之间的两位有效小数。在人造数据集1中，控制顶点的平均度数d相同，都为1.23.顶点大小从1k递增到10k.每次递增1k：在人造数据集2中，控制顶点大小一定，都为1k.平均度数取3-7.5.每次递增0.5。人造数据集3是一个小规模图集合，顶点大小从10递增至50.平均度数都为3。

3.2实验结果

贪心算法在求MST_max時，如果图不连通，则求最可靠的最小生成森林MSF_max。具体来说，当算法求得一棵生成树A时，若A中顶点数小于图G的顶点数|V|，则将A加入到MSF_max中，同时随机选取一个不在A中的顶点作为新的根节点，生成另外一棵生成树，直至MSF_max覆盖所有G中的全部顶点。

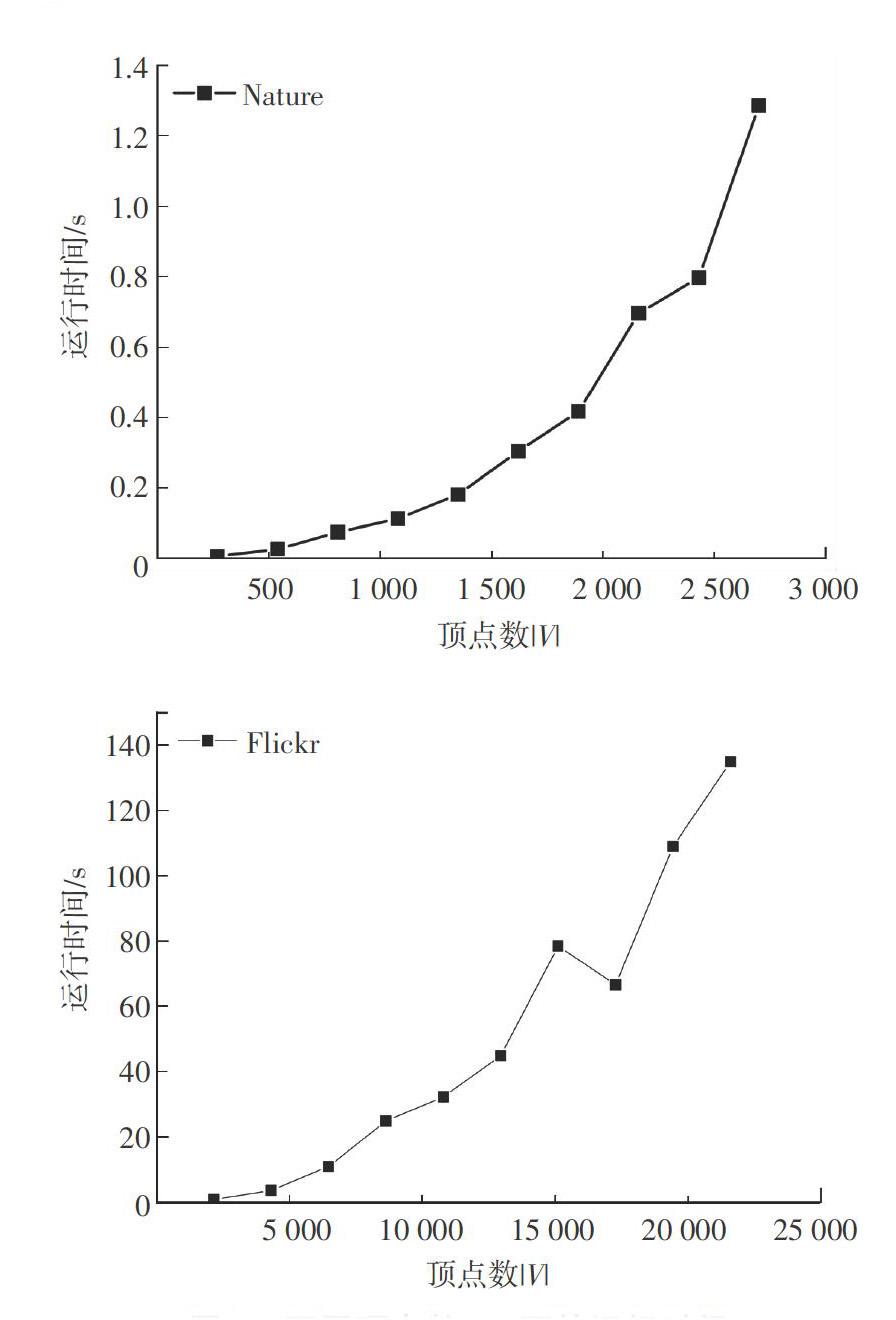
首先测试贪心算法在不同图规模下的性能表现。在合成数据集Nature和Flickr上，逐步抽取其上的子图进行测试，子图大小为原图的10%-100%，运行时间随顶点大小的变化如图3所示。实验结果表明运行时间随顶点数|V|的增加大致呈抛物线增长趋势，与上一节分析的算法运行时间O（d²|V|²）一致，另外在Flickr数据集上，图规模为（17273.102356）时的运行时间比图规模为（15113.97743）反而少，这是因为（17273.102356）的平均度数d为5.9.比（15113.97743）上的平均度数6.4小，接下来测试平均顶点度数对运行时间的影响。

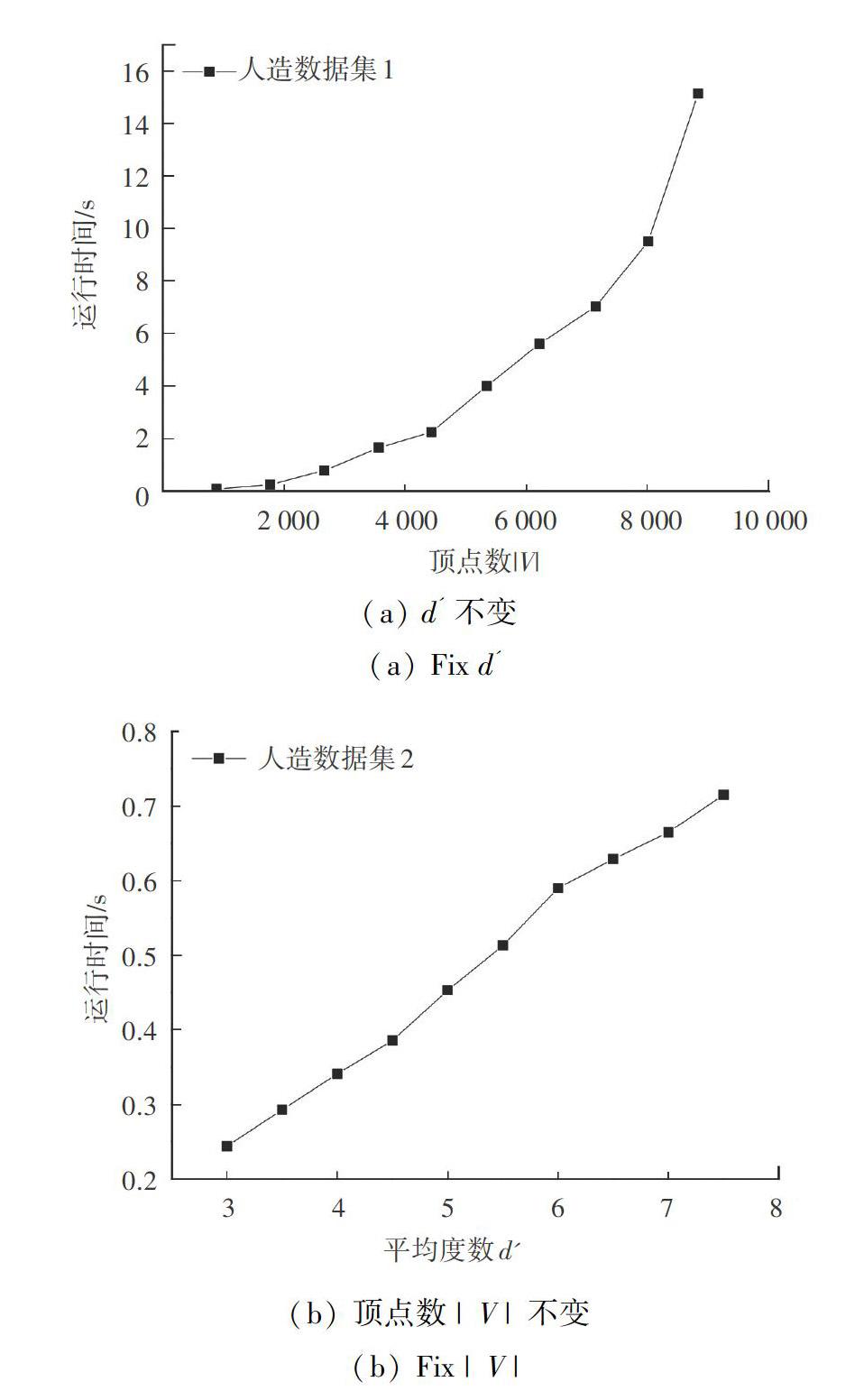
在人造数据集1中，顶点平均度数d一定，都为1.23.在其上运行贪心算法，测试顶点大小对运行时间的影响，结果如图4（a）所示。在人造数据集2上，顶点大小固定，都为1k.边的大小从3k递增到7.5k.即顶点平均度数取3-7.5.运行结果如图4（b）所示。

由图4（a）分析可知，当平均顶点度数d一定时，算法的运行时间随|V|的增大呈抛物线增长趋势，并且期间没有异常点出现。图4（b）中的实验结果表明，当顶点数一定时，运行时间随平均度数d增加而呈线性增长。

若要验证贪心算法得到的最小生成树与精确解得到的最小生成树是否一致，需要枚举所有可能的最小生成树，枚举代价非常大，为O（2^|E|），這为验证工作增加了很大困难，因此需要设计一个随机算法用来对比实验结果，

随机算法每次向树A中随机添加队列S中的一条边，由于最小生成树的存在概率等于每次迭代时加入A中边的概率P累乘，当图规模太大时，最小生成树的概率P很小，为了方便实验数据对比，取其对数得到logP从而将其放大，由于log函数具有单调递增性，所以不会影响实验对比结果。在人造数据集3小图上进行实验，随机算法执行3次，实验结果如图5所示。

由图5上的结果可见，随着顶点数增多，贪心算法求出的最小生成树的概率比3次随机算法求得的最小生成树概率大很多，并且权值更小，这在很大程度上说明了贪心算法求出的MST_max是精确解的一个很好的近似。

4结束语

本文研究了不确定图上最可靠的最小生成树问题。最可靠的最小生成树代表了不确定图上最稳定的连通分支，具有广泛的应用价值。精确求解算法的时间开销非常大，因此本文给出一个多项式时间的启发式贪心算法，实验结果表明该算法在大多数情况下能够得到最优解。