School of Chemical Engineering,Sichuan University,Chengdu 610065,China

Keywords:Ammonium dihydrogen phosphate Solubility Water-methanol system

ABSTRACT The solubility of ammonium dihydrogen phosphate(MAP)in the water-methanol system is essential for antisolvent crystallization studies.To investigate the effect of methanol on the solubility of MAP in water,the solubility of MAP in the water-methanol system was determined by dynamic method and static equilibrium method at temperatures ranging from 293.2 to 343.2 K at atmospheric pressure.Results showed that the solubility of MAP increased with the increase of temperature and the increase of water mole fraction in the water-methanol system.The experimental solubility data were correlated with the modified Apelblat equation,the combined nearly ideal binary solvent/Redlich-Kister(CNIBS/R-K)model and the Jouyban-Acree model.The calculated results based on these three models were in very good agreement with the experimental data with the average relative deviations of 0.65%,0.97%,and 5.38%,respectively.Simultaneously,the thermodynamic properties of the MAP dissolution process in the water-methanol system,including Gibbs energy change,enthalpy,and entropy were obtained by the Van't Hoff equation,which can be used to assess the crystallization process.

1.Introduction

Ammonium dihydrogen phosphate(MAP,NH4H2PO4)is an important product in the phosphorus chemical industry and has a wide range of applications in various fields,such as fertilizers,nonlinear optical materials,flame retardants,wastewater treatment[1-5].The MAP production process comprises the reaction between phosphate and ammonia,crystallization,drying,and so on[6,7].Among them,the crystallization of MAP is a key step and the traditional crystallization route is in aqueous solution,leading to high energy consumption and production costs.Generally,solubility is a basic thermodynamic parameter in crystallization process.Mullin et al.measured the solubility of MAP over the temperature range 20-40°C,and investigated the growth kinetic of MAP crystal[8,9].Yang et al.researched the solid-liquid phase equilibrium for urea phosphate+MAP+water to prepare the urea phosphate in the ternary system[10].Eysseltová et al.provided an overview of solubility of ammonium phosphates[11].In recent years,the antisolvent crystallization is proposed as a promising way to save energy and improve the crystal quality,because a suitable antisolvent can decrease the solubility of salt in water[12-15].In our previous study,a process to produce MAP using ethanol as the antisolvent was proposed and this has an important guiding significance on the production of MAP[16].However,it was difficult to recycle the ethanol by conventional distillation,because the water-ethanol system generates an azeotrope(89.5%of ethanol)at the temperature of 78.1°C and under atmospheric pressure.

Methanol is the simplest alcohol and shares many similarities with ethanol.It can also be used as an antisolvent.Importantly,there exists no azeotrope in the methanol-water system.It is also well known that methanol is cheaper than ethanol due to the methanol overproduction in China.Besides,methanol is a byproduct in some enterprises that produce MAP.Hence,it would be a good choice to use methanol as an antisolvent in the crystallization of MAP.The process is schematically shown in Fig.1,and an amount of recycled methanol is added to the MAP water solution to lower the solubility of MAP and the MAP product is produced by the antisolvent crystallization.The residual fluid obtained is distillated to recycle methanol.The solubility plays a crucial role in the crystallization process,but relevant data about the solubility in the water-methanol system are not available in any publications.Therefore,we report here the solubility of MAP in the water-methanol system.

In this work,the solubility of MAP in the water-methanol system is determined at temperatures ranging from 293.2 to 343.2 K and the experimental data were correlated with the modified Apelblat equation,combined nearly ideal binary solvent/Redlich-Kister(CNIBS/R-K)model and the Jouyban-Acree model.Besides,the thermodynamic properties of the MAP dissolution process in the water-methanol system,including Gibbs energy,enthalpy,and entropy were obtained by the Van't Hoff equation.

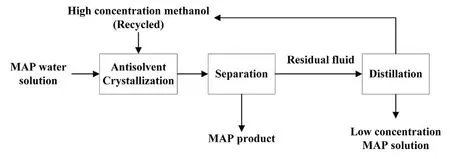
Fig.1.A flow-diagram of the antisolvent crystallization process in the water-methanol system for the production of ammonium dihydrogen phosphate(MAP).

2.Experimental

2.1.Materials

MAP(analytical grade)with a purity greater than 99.0%was from the Sinopharm Chemical Reagent Co.,Ltd.Methanol(analytical grade)was from the Chengdu Kelong Chemical Co.,Ltd.and its purity was greater than 99.5%.Deionized water was used in the experiments.

2.2.Apparatus and procedure

In order to ensure the accuracy of measurement,the solubility was relatively low with mole fraction of water from 0 to 0.6 and it was determined by a static equilibrium method[17-20];the solubility was relatively high with mole fraction of water from 0.6 to 1 and it was determined by a dynamic method[21-23].The experimental apparatus,as shown in Fig.2,was presented in detail in previous publications[16].It consisted of a jacketed-glass bottle(about 500 ml effective volume),a magnetic stirrer,a thermostatic water bath and a mercury thermometer.The temperature was controlled by a thermostatic water bath and determined by a mercury thermometer with an accuracy of 0.1 K.The magnetic stirrer was used to provide an agitation to accelerate the dissolution and the equilibration process.To accurately weigh the mass of a chemical reagent,an electronic balance with a precision of 0.0001 g was used.

Fig.2.Experimental device for solubility measurement:1,thermostatic water(inlet);2,jacketed-glass bottle;3,mercury thermometer;4,magnetic rotor;5,thermostatic water(outlet).

The solubility of MAP in the water-methanol system was determined as follows.A water-methanol solution with known composition was prepared and the mole fraction of water,x1,was calculated by the equation,

where m1,m2,M1,and M2represented the mass of water and methanol and the mole mass of water and methanol,respectively.When x1ranged from 0 to 0.6,the solubility was determined by the static equilibrium method.For each determination,an excessive amount of MAP was added to the water-methanol system with a known composition.The mixed solution in the sublayer of the jacketed-glass bottle,was stirred for 3.5 h until it reached the equilibrium state.Then,the solution was left static for 1 h,allowing the undissolved MAP to settle down.The supernatant liquid sample obtained was analyzed by the gravimetric method of quinoline phosphomolybdate.When x1ranged from 0.6 to 1.0,the determination method was switched to the dynamic method.The water-methanol solution of known composition was added to the jacketed-glass bottle and kept at a desired temperature;then MAP with known weight was added sequently.When the last small addition was not completely dissolved,the solid liquid phase equilibrium was established.The total addition amount before the last addition was the solubility of MAP in this water-methanol solution.The solubility of MAP expressed as MAP mole fraction in the water-methanol system,xA,was calculated as follows,

where mA,and MArepresent the mass and the mole mass of MAP,respectively.

3.Results and Discussion

3.1.Solubility of MAP in the water-methanol system

The mole fraction of MAP in the water-methanol system at temperatures from 293.2 to 343.2 K were listed in Table 1,and dotted in Fig.3.It was obvious that the solubility of MAP was related to the concentration and temperature of the water-methanol system.The solubility of MAP increased with the increase of temperature and the increase of the water mole fraction in the water-methanol system.At a constant temperature,the solubility increased slowly first,and then increased rapidly when the mole fraction of water(x1)was more than 0.6.It can be seen that the mole fraction of MAP was very small and its variability with the change of temperature was not obvious when the mole fraction of water was less than 0.6.When the binary solvent has a low mole fraction of water(x1=0-0.6),the solubility of MAP increased slowly with the increase of temperature,however it increased dramatically at a higher water content(x1=0.6-1).Compared with the solubility in pure water(x1=1),the MAP solubility was greatly reduced as the amount of methanol increased in the water-methanol system.Therefore,methanol can be used as an effective antisolvent in the MAP crystallization process.

3.2.Solubility model and parameterization

3.2.1.Modified Apelblat equation

The modified Apelblat equation is a semiempirical model which deduced from the Clausius-Clapeyron equation,and it is widely applied to calculate the solubility of solute in solution.The equation is correlated solubility and temperature in a solvent with known composition[24-26],and it can be expressed as,

where xAand T are the mole fraction of solute in the solution and the absolute temperature(K),respectively.A,B,and C are the parameters for the model.

Table1 The mole fraction solubility of MAP in experiment(),the calculated solubility(),and the relative absolute deviations(RAD)for MAP in the water-methanol system from 293.2 to 343.2 K at p=0.1MPa①

Table1 The mole fraction solubility of MAP in experiment(),the calculated solubility(),and the relative absolute deviations(RAD)for MAP in the water-methanol system from 293.2 to 343.2 K at p=0.1MPa①

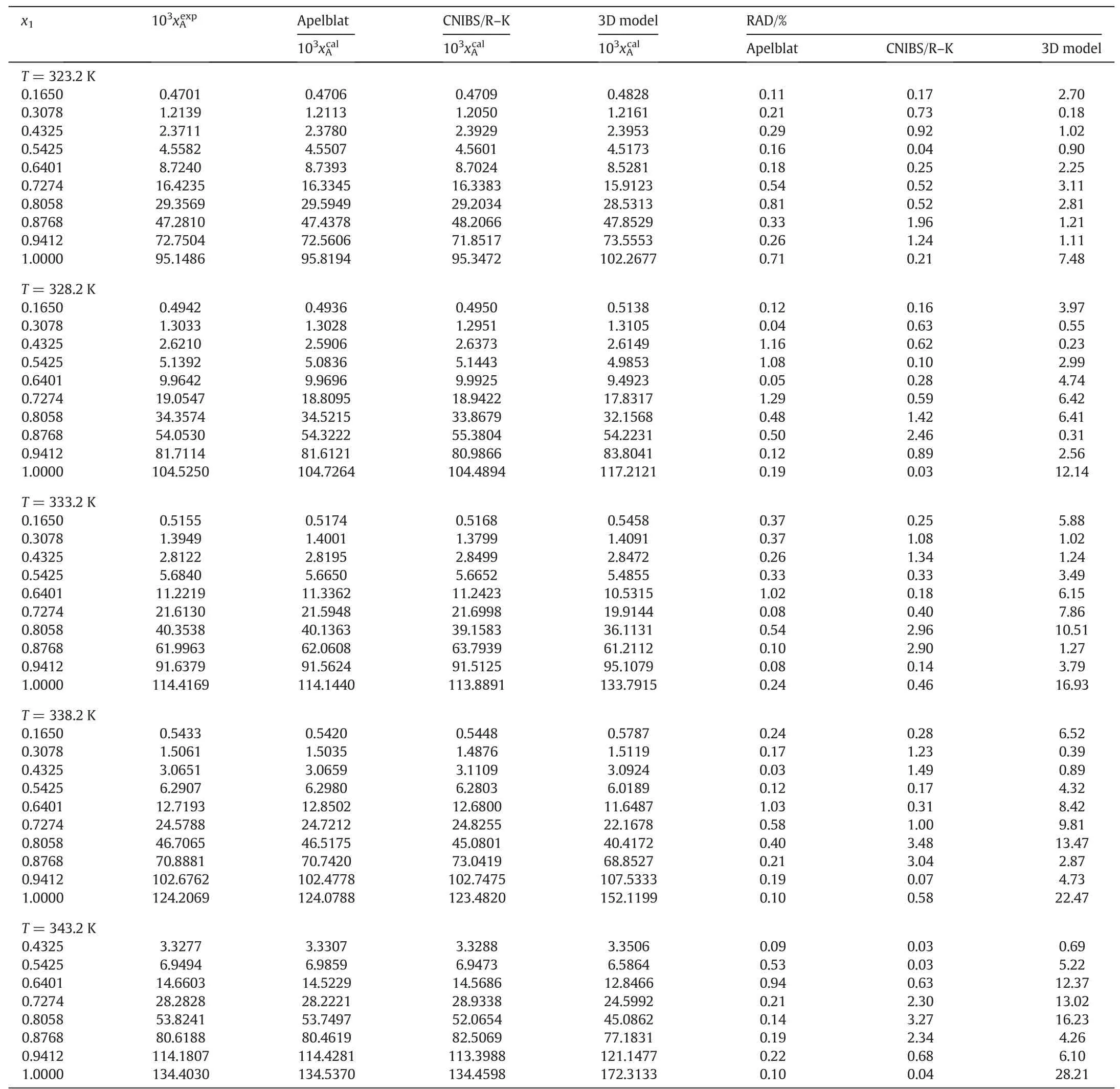
Table 1 (continued)

3.2.2.CNIBS/R-K model

The Combined Nearly Ideal Binary-Solvent/Redlich-Kister(CNIBS/R-K)model is one of the theoretical models,and it is a power series equation which associated the solubility with the concentration of one of the solvents in binary solvent systems[27-29].The model is broadly used to calculate the solubility in binary solvents at constant temperature,and it is described as follows,

where B0,B1,B2,B3,and B4are the parameters of the simplified CNIBS/R-K model in the mixed solvents.

3.2.3.Jouyban-Acree model

The Jouyban-Acree model is a 3D model and it is presented for the calculation of solubility in the mixed solvents system[30].In this model,the binary and ternary interactions have all been included.According to this model the solubility can be calculated as,

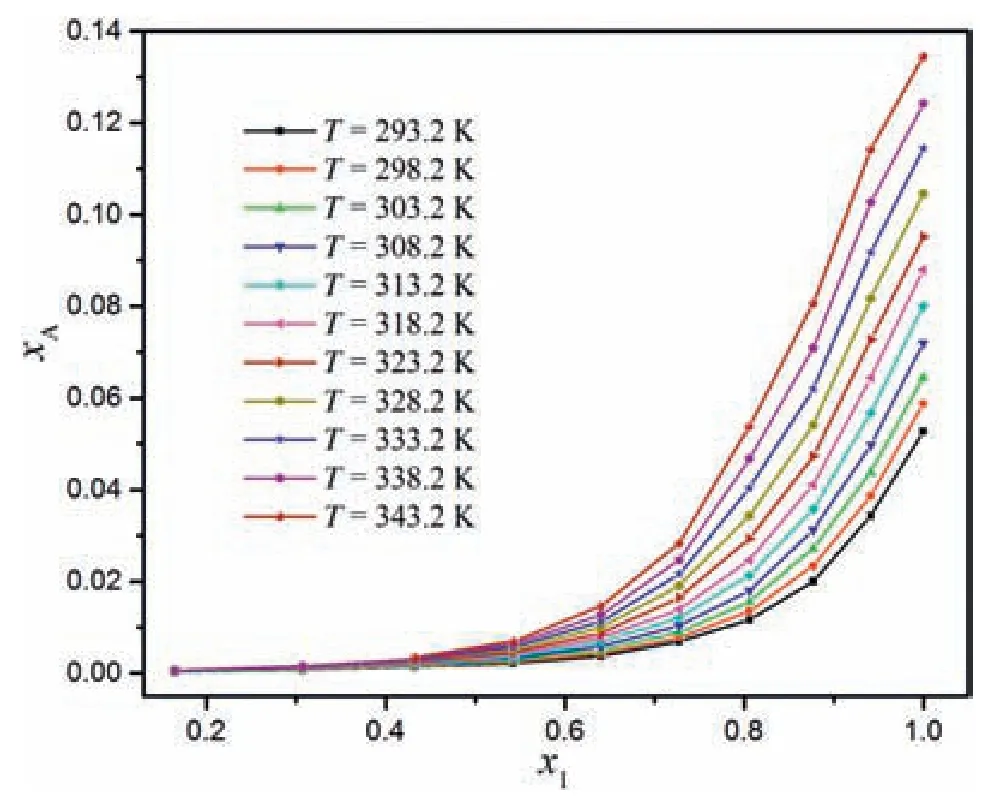
Fig.3.The solubility of MAP(expressed as MAP mole fraction xA)in the water-methanol system as a function of the mole fraction of water in the solvent(x1)at different temperatures.

where A1,A2,B1,B2,J0,J1,and J2are the parameters of the Jouyban-Acree model for the mixed solvent system.

3.2.4.Model parameterization

The solubility of MAP in the water-methanol system at different temperatures was fitted by the three models mentioned above and the corresponding parameters were obtained as listed in Tables 2-4.In addition,the solubility curves calculated by the three models were represented in Figs.4-6,respectively.

Table 2 Parameters of the modified Apelblat equation for the MAP solubility in the water-methanol system

Table 3 Parameters of the simplified CNIBS/R-K Model for the MAP solubility in the water-methanol system

Table 4 Parameters of the 3D Jouyban-Acree model for the MAP solubility in the water-methanol system

3.3.Relative absolute deviations

To evaluate the deviation between the experimental data and the model calculation values,the relative average deviations(RAD)are calculated as follows,

Fig.4.The solubility of MAP(expressed as mole fraction xA)in the water-methanol system:x1represented the mole fraction of water in the binary solvent,the solid lines were calculated with the modified Apelblat equation.

where N is the number of experimental points.are the experimental and calculated solubility of MAP in the water-methanol system,respectively.The values of RAD are calculated for the three different models and listed in Tables 1-4.It can be seen clearly that the RAD values are very small for all the three solubility models.The RAD values are 0.65%,0.97%,and 5.38%for the modified Apelblat equation,for the CNIBS/R-K model,and for the Jouyban-Acree model,respectively.The coefficient of determination(R2)is very good and all of them reach 0.999 for the model of modified Apelblat equation and CNIBS/R-K.For the Jouyban-Acree model,the R2is 0.9981.The results show that the solubility of MAP in the water-methanol system can be predicted by the three solubility models,the values of RAD and R2indicate that the predicted values are reliable.By comparing the three models,the accuracy of the modified Apelblat equation is the highest,the Jouyban-Acree model is the lowest,and the CNIBS/R-K model is intermediate.The modified Apelblat equation is used to predict the solubility of MAP in the same binary solvent system of identical composition but at different temperatures,while the CNIBS/R-K model is used to predict the solubility at a certain temperature at different concentrations of solvents.For the modified Apelblat equation and the CNIBS/RK model,it requires a lot of model parameters to describe the solubility of MAP in the water-methanol system.For the Jouyban-Acree model,although it has a larger RAD and a lower R2,the Jouyban-Acree model considers the combined impact of the temperature and the composition of the binary solvent,and the needed model parameters are much less than the model parameters of the modified Apelblat equation and the CNIBS/R-K model.Therefore,the Jouyban-Acree model is considered sufficient to predict the solubility of MAP at different temperatures and component concentrations in the water-methanol system.

Fig.5.Natural logarithm mole fraction solubility of MAP in the water-methanol system:x1represented the mole fraction of water in the binary solvent,the solid lines were calculated with the CNIBS/R-K model.

3.4.Thermodynamic properties of the solution

According to the thermodynamic principles of solid-liquid equilibrium,the Van't Hoff equation can be used to describe the relationship between the absolute temperature and logarithm of mole fraction solubility.The equation is expressed as follows[31,32],

Fig.7.Natural logarithm of the MAP solubility versus 1/T for the Van't Hoff plots in the water-methanol system:■x1=1.0000;○x1=0.9412;▲x1=0.8768;▽x1=0.8058;◆x1=0.7274;◇x1=0.6401;▼x1=0.5425;△x1=0.4325;●x1=0.3078;□x1=0.1650;x1represented the mole fraction of water in the binary solvent.

Table 5 Standard molar dissolution enthalpy and entropy for the MAP in the water-methanol system

The Van't Hoff plot of the MAP solubility in the water-methanol system is presented in Fig.7 and the values ofobtained are listed in Table 5.From Table 5,it can be obviously seen that the values ofare positive,and the values ofare mostly positive and while some are negative.Because the values ofare positive,it can be proved that the MAP dissolution process is endothermic,which confirms that the solubility of MAP increases with the increase of temperature in the water-methanol system.The value ofis maximum when the molar fraction of water is 0.8058 at the investigated experimental points.It can be speculated that the solubility of MAP is mainly affected by temperature at a particular concentration of water.When the values ofwere negative,the contribution ofto the Gibbs energy is positive,which substantiate the very low solubility of MAP in methanol-rich binary solvents.The solubleness of MAP increases when the values ofbecome more and more positive,with the increase of water content in the water-methanol system.

Obviously,Eq.(9)shows that theis a linear function of the natural logarithm of the MAP solubility at a constant temperature.From Table 6,it can be seen clearly that the value ofdecreased with the increase of the mole fraction of water in the water-methanol system at a constant temperature.It reveals that a smallervalue means better solubleness and a larger solubility.All thevalues are positive,which indicates that the MAP dissolution process is not spontaneous in the water-methanol system.

4.Conclusions

The solubility of MAP in the water-methanol system at atmospheric pressure and at the temperatures from 293.2 to 343.2 K was determined with the static equilibrium method and the dynamic method.Results show that the solubility of MAP increased with the increase oftemperature and the increase of the mole fraction of water in the binary solvent.The modified Apelblat equation,CNIBS/R-K model and Jouyban-Acree model were successfully applied to fit the experimental solubility data with the average RAD of 0.65%,0.97%,and 5.38%,respectively.On the basis of these results,it can be concluded that methanol can be used as an effective antisolvent in the crystallization process of MAP.Furthermore,the thermodynamic properties such as enthalpy,entropy and Gibbs energy change associated with the MAP dissolution process were calculated by the Van't Hoff equation;results indicated that the dissolution process of MAP in the water-methanol system was endothermic and nonspontaneous.

Table 6 The molar Gibbs energy change ΔsolG/kJ ∙mol-1 for the MAP dissolution at different temperatures in the water-methanol system

Table 6 The molar Gibbs energy change ΔsolG/kJ ∙mol-1 for the MAP dissolution at different temperatures in the water-methanol system