College of Chemical Engineering,Qingdao University of Science&Technology,Qingdao 266042,China

Keywords:Big data Fault diagnosis Mutual information TE process Process modeling

ABSTRACT A large amount of information is frequently encountered when characterizing the sample model in chemical process.A fault diagnosis method based on dynamic modeling of feature engineering is proposed to effectively remove the nonlinear correlation redundancy of chemical process in this paper.From the whole process point of view,the method makes use of the characteristic of mutual information to select the optimal variable subset.It extracts the correlation among variables in the whitening process without limiting to only linear correlations.Further,PCA(Principal Component Analysis)dimension reduction is used to extract feature subset before fault diagnosis.The application results of the TE(Tennessee Eastman)simulation process show that the dynamic modeling process of MIFE(Mutual Information Feature Engineering)can accurately extract the nonlinear correlation relationship among process variables and can effectively reduce the dimension of feature detection in process monitoring.

1.Introduction

In recent years,the industrial system is developing in the direction of large-scale installations and complex process.How to use process monitoring and fault diagnosis technology to guarantee its safety,long cycle,and high quality operation is of great importance.Therefore,the concept of feature engineering in machine learning field has gradually developed into a hotspot of process monitoring technology[1,2].For feature engineering,its difficulty lies in how to find new variables that can characterize the main feature of the data because it is essentially a complex combinatorial optimization problem[3].

In the feature modeling process,each feature variable has two possible states:reserved or excluded.The element number in the state set can be obtained using probability analysis algorithms such as Bayesian network and neural network[4,5].Generally,if there are N feature variables,the number of elements in the state set is 2N.Therefore,from the algorithm point of view,the time complexity of solving this problem is exponential in an exhaustive way.When N is large enough,feature selection will cost a lot of time and computing resources[6].In the field of information theory,mutual information is a very useful measure to explain the correlation information for a random variable in a vector.The aim to obtain the correlation of mutual information is to measure the shared information between two variables,not limited to a simple linear relationship only.This is a nonparametric and nonlinear measure index to analyze the main factors in multiple variables.At present,it has attracted more and more attention in the field of data analysis and numerical modeling[7-10].There also are some applications in the field of multivariate statistical process monitoring based on mutual information analysis and process data[11].

In recent years,the research of multi-variable feature extraction method based on PCA has received extensive attentions from industrial and academic fields[12-15].Its basic idea is to dig out potential information that can reflect the running status of process based on the data collected in industrial processes.This method usually conducts a projection of original data to the low dimension subspace after analyzing the characteristics of the high dimensional process data,thus providing the information to the operator in the form of statistics.Therefore,it is suitable for monitoring modern large-scale complex industrial processes.Generally,the classic feature extraction method like PCA determines the direction of the reduced dimension projection by calculating the covariance matrix or the correlation matrix of the data set.The latent variables extracted(i.e.,principal components)can comprise the correlation characteristics of the original data space.Although the PCA method is concise and easy to analyze process data,the covariance or correlation coefficient can only reflect the linear correlation among variables,not the nonlinear relationship[16].Therefore,there are great limitations for the traditional PCA method to extract data features.The nonlinear process monitoring method based on the modified PCA methods like kernel PCA(KPCA)can effectively deal with the nonlinear process data.However,for the transformed correlation among the high dimensional spatial data,the KPCA method still calculates the correlation coefficient without involving the nonlinear term[17-20].

The normal operation of chemical process must follow the first law,i.e.,many variables often affect each other and change dynamically with time.In such a case,there are often complex correlation characteristics among the process variables.Fault diagnosis(including fault monitoring)is a concept emerging in the field of computer,which is based on the dynamic process modeling of characteristic engineering.Compared with the traditional dimensionality reduction methods like PCA,ICA(Independent Component Correlation Algorithm),etc.[21-25],the relevant literature on fault diagnosis in the chemical industry domain is not much.Feature engineering finds the best feature subset by reducing the number of samples,thereby simplifying the complex association features between variables.Therefore,this paper proposes a mutual information feature based fault monitoring method for chemical processes.The concept of mutual information features is obtained by analyzing the nonlinear correlation between variables in chemical process to optimize the characteristics of variable set.Mutual information is used to find the correlation of process variables,construct and select the optimal feature subset.The selected features are called mutual information features.In this method,feature selection and feature extraction are performed by mutual information and dimension reduction,which makes up for the deficiency of traditional feature selection and extraction algorithms.

This paper is organized as follows.Firstly,the proposal is described in detail.It preprocesses data based on the characteristics of variable correlation,and selects the best variable subset using mutual information with the nonlinear and linear correlation information of the process.Afterwards,the process features are extracted by the PCA dimensionality reduction method and the corresponding PCA detection model is established hereafter.Secondly,through the application to the Tennessee-Eastman process,the validity and feasibility of the fault monitoring method based on the mutual information feature engineering are verified.

2.Fault Monitoring Based on Feature Engineering in Chemical Process

2.1.Description of fault monitoring based on feature engineering

Feature engineering is an essential activity to extract features from the original data to a maximum extent by algorithm and model.The method of fault monitoring for chemical process based on feature engineering is illustrated in Fig.1.

In feature engineering,the data is preprocessed first to select the optimal subset for different dimensionless features with missing values of data processed[26].

After data preprocessing,feature selection(also-called FSS,feature subset selection),is conducted from two aspects:the feature is divergent or not.In the practical application of feature engineering,interdependence exists between features with the following consequences:the more the number of features is,the longer it takes to analyze features and train models,and the easier it causes dimensional disaster.Additionally,the more complex the model is with increasing features,the lower its generalization ability becomes.Feature selection can eliminate irrelevant or redundant features to improve the accuracy of the model and reduce the running time.Consequently,it can select the real related features to simplify the model,benefiting a fundamental understanding of the process of data generation.

For feature extraction,the common methods used in engineering are linear methods like variance,correlation coefficient,and nonlinear methods like mutual information.The variance and correlation coefficient can only measure the linear correlation[27].Comparatively,the mutual information coefficient can measure all kinds of correlation well,but its computation is relatively complex.Because the correlation of each feature is extracted by mutual information,the feature extraction involves many relevant features.The correlation between each feature and response variables is calculated with a subset of features to facilitate modeling.

After feature extraction,the model can then be trained directly.It is necessary to reduce the dimension of feature matrix because of the high computation cost and long training time caused by the oversize of the feature matrix.The commonly used methods for reducing dimension in chemical process are PCA,LDA(Linear Discriminant Analysis),and the related improved algorithms[28-30].There are many similarities between PCA and LDA to map the original sample to the lower dimension of the sample space,but their mapping target is different:PCA treats the sample after mapping with maximum divergence while LDA does after mapping with best classification performance.Therefore,PCA is used to reduce dimension for verifying the effectiveness of the method in the TE process in this work.

2.2.Feature subset selection based on mutual information

2.2.1.Mutual information

Mutual information is a nonparametric and nonlinear measure index in information theory.It is also a typical method to analyze the model of computational linguistics,with the aim of evaluating the correlation between two measured variables.If the joint probability distribution function of two random variables x and y is p(x,y),the marginal probability distribution function is p(x)and p(y)respectively,and mutual information I(x,y)is defined as[31-33]:

If there is no overlapping information between x and y,namely mutual independence,the mutual information value is equal to 0.Conversely,the mutual information value will be larger than zero.It is worth noting that I(x,y)requires the probability of distribution density of the known variables.In this paper,the kernel density estimation method is used to determine the corresponding probability values,as shown in Eq.(2)[34].

Fig.1.Fault monitoring based on feature engineering in chemical process.

Fig.2.Optimal subset selection based on mutual information.

2.2.2.Modeling methods

Considering the interdependence between variables in complex dynamic processes,different measurement variables will have differentsequence correlations,and the interaction between variables will be reflected at different sampling times.The diagram of modeling methods is shown in Fig.2.In order to better describe the dynamics of each measurement variable,the specific implementation steps are given as follows:

(1)Introduce continuous time measurement values for each variable to form an augmented data matrix Xa;

(2)Calculate a measurement variable Xiwith all variables xj(j=1,2,…ml)in Xa,that is Mi,j=I(xi,xj)

Fig.3.TE process.

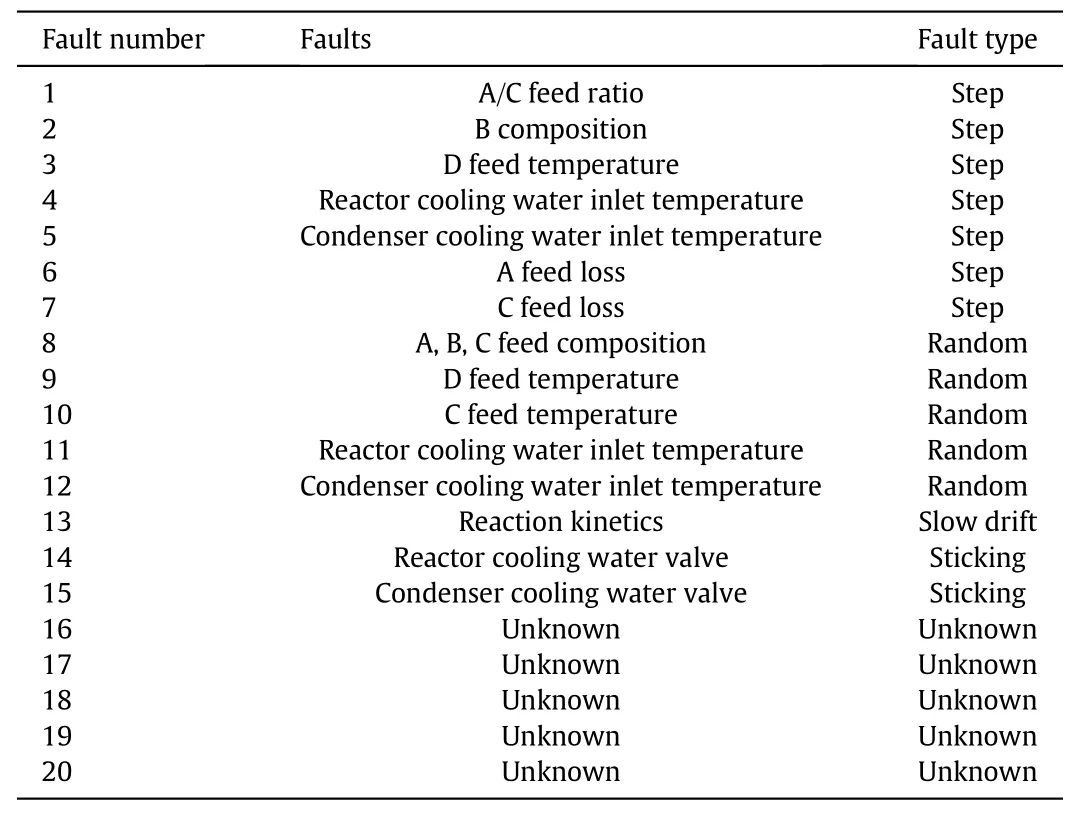
Table 2 TE process faults

Fig.4.The number of principal component selection based on PCA.

(3)With the descending order of Mi,j∈R1×ml,select highly relevant variables to form the variable sub-block Xicorresponding to the top k maximum values.

(4)Select the feature variables from the subset of m variables and construct the best feature subset.

The variables obtained in each feature subset at different times describe the dynamics of the corresponding measurement variables.Compared with the analysis of PCA that directly uses all variables,this variable selection method can eliminate the“interference”effect of some unrelated variables,thus make the sub-block PCA model reflecting the dynamic characteristics of each measured variable better.Therefore,when monitoring the operation state of the dynamic process,the feature engineering method based on mutual information should be expected to achieve a better fault detection effect.

2.3.Feature extraction

The PCA method is concise and easy to implement for analyzing process data.It is assumed that there are m sensor acquisition variables under normal working conditions,and each sensor is sampled n times.Then,the data matrix X=[X1,X2,……Xi,Xm]∈Rn×m,where Xiis n×1 data vector,each data vector represents a variable of the process,m is the number of sample variables,n is the number of data.Among them,the covariance of X is[35]:

First,the covariance matrix C of X is obtained:

where,Ci,j=COV(Xi,Xj).

Then the eigenvalues and eigenvectors corresponding to the covariance matrix C are calculated,and C is decomposed by feature decomposition:

The corresponding eigenvalues are{λ1,λ2,λ3…,λm},and the eigenvectors are{P1,P2,P3,…,Pm}.A set of orthonormal is found to guarantee the maximum variance after transformation.The PCA algorithm reduces the dimension by mapping the high-dimensional data to the low-dimensional space,and the mapping direction of the data is the direction in which the data variance changes greatly.Theprojection in the direction of the larger variance is caused by the fluctuation of the data itself,and in the direction of the smaller variance is caused by the noise.When the difference in the projection direction is large,the data is scattered,and also contains most of the information of the original data,which is called the maximum variance theory.So the largest variance dimension is selected to guarantee that the most information is stored.If the variables between the two dimensions are strongly correlated,the data with respect to the two dimensions will reach a straight line,meaning that partial data of the dimensions is redundant.In this situation,the transformed matrix is Ti=Xpi,where the rows form the principal components.The number of principal components is determined according to the principal component cumulative contribution rate(CPV):

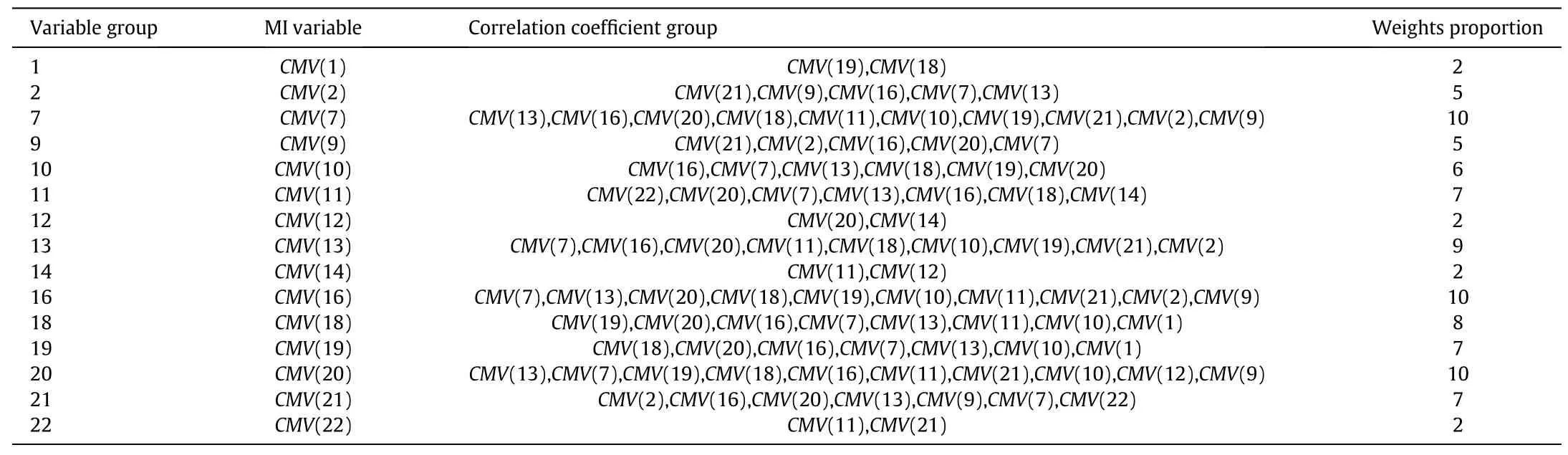
Table 3 Correlation set of continuous measurement variable

Fig.5.The number of principal component selection based on MIFE.

The T2=xTPΛ-1PTx statistic of principal component space T2can then be constructed,where Λ=diag{λ1,λ2,…λk}.The corresponding control limit with a confidence interval of 99%is obtained by[34]:

Fig.6.PCA monitoring results of fault 1.

Fig.7.MIFE monitoring results of fault 1.

Above all,the steps of fault monitoring for chemical process based on mutual information feature engineering are summarized as follows:

(1)Normal data of variables are normalized to form the modeling database.

(2)The probability of distribution density of time series variables is calculated to obtain the mutual information between variables.

(3)According to the mutual information value among variables,the process variables are divided into k related subsets and one non-related subsets to construct the best feature subset.

(4)The original PCA decomposition of the optimal subset data is carried out,and the K principal components are extracted with the CPV criterion.

(5)The best characteristic subset T2statistic is calculated,and its control limit is derived from Eq.(7).

3.Case Studies

In order to verify the feasibility of the fault monitoring method based on mutual information feature engineering modeling,this method was applied to the TE benchmark example.Various factors affecting the performance of this method are discussed in this section.

3.1.Process description

Fig.9.MIFE monitoring results of fault 8.

In this paper,a typical Tennessee Eastman process simulation system is used to verify the effectiveness of the proposed method.The process structure of TE is shown in Fig.3.It is a typical chemical process published by Downs and Vogel in the Computers&Chemical Engineering journal in 1993,mainly including 5 typical units:reactor,condenser,gas liquid separator,desorption tower,and circulating compressor.The process consists of 12 operating variables and 41 measurements variables,20 pre-set failures,and 6 control modes.Each training data consists of 480 sets of sample data,and the test data consist of 960 sets of sample data.

In this case study,22 continuous measured variables can effectively represent the state of the whole process,so they are used as the initial detection variables,as shown in Table 1.The 20 faults are shown in Table 2.

3.2.Feature subset selection

In order to prove the effectiveness of the method,this example selects fault 1,fault 8 and fault 13(three different kinds of fault)to carry out fault monitoring task.First,the mutual information of 22 continuous measured variables in the TE process is acquired in the normal state,and quantified in the abnormal state.The correlation variable subset is shown in Table 3.The feature variables with large weights reflect the nonlinearity and linear correlation between variables.Therefore,after eliminating the correlation redundancy,the related feature variables remain as CMV(2),CMV(7),and CMV(11).By classifying the mutual information variables and carrying out the weight ratio analysis,the optimal subset is further obtained as CMV(1),CMV(2),CMV(3),CMV(4),CMV(5),CMV(6),CMV(7),CMV(8),CMV(11),CMV(12),CMV(14),CMV(15),and CMV(17).

Fig.10.PCA monitoring results of fault 13.

Fig.11.MIFE monitoring results of fault 13.

3.3.Feature extraction based on PCA

The 500 groups of samples collected under normal working conditions are used as training sets of PCA and MIFE(Mutual Information Feature Engineering),and 960 groups of samples under normal conditions are used as validation sets of PCA and MIFE.The selection effect of latent variables based on PCA and MIFE is shown in Figs.4 and 5.First,considering the principal element contribution rate and the maximization of variance,the PCA monitoring model reorders the eigenvalues of the principal component from large to small,and selects first 13 variables according to the criterion of the CPV≥85%,as shown in Fig.4.The MIFE model has selected 11 corresponding variables to reconstruct the principal subspace,as shown in Fig.5.Compared with the dimensionality reduction feature extraction of PCA,the number of principal component based on MIFE is reduced by 10%.The contribution of some principal component contributions to MIFE is relatively low,indicating that the redundant information of nonlinear dependent variables in the process is effectively removed.

In order to demonstrate the superiority of the MIFE model,three typical faults 1,8 and 13 are selected for the key analysis.The monitoring effect of fault 1/8/13 based on PCA and MIFE is shown in Figs.6-11.It can be concluded that the two methods can directly detect the time of failure appearance.Compared with the MIFE model for fault 1,the missing rate of the PCA model gradually increases at the 533-960 sample points,as shown in Figs.6 and 7.Also,the missing detection rate of the PCA model increases gradually at 163-231 sample points.In contrast,the MIFE model can trigger the fault alert continuously from the fault signals.Even though the automatic loops pull off the effect of the process triggering device,the MIFE model still maintains a higher fault detection rate.Additionally,it is obvious that the traditional PCA method has difficulty in finding fault 8.For the MIFE method,only 6.375% of the fault samples are not detected and the failure rate is low,as shown in Figs.8 and 9.For the slow drift fault 13,the PCA model has poor detection ability before the 203 fault sample points,while the MIFE method can detect fault 13 effectively after the 174 sample points.The failure alarm rates of PCA and MIFE are shown in Table 4.From Table 4,it can be seen intuitively that the failure alarm rate of the proposed method MIFE is lower than that of PCA.

After above discussions,it is necessary to verify the failure rate of the MIFE method.Generally,a lower failure rate corresponds to a high falsealarm rate because the normal data sample error is also identified as failure.With 960 data collected under another set of normal working conditions,the false alarm rates of PCA and MIFE statistical indexes are tested.The corresponding results are shown in Table 5.We can see that the average false alarm rate of PCA is slightly lower than that of the MIFE algorithm.In previous discussion we know that the failure alarm rate of MIFE is significantly lower than PCA.For process monitoring,a lower failure alarm rate is better when false alarm rate is nearly the same.So through comparative analysis,the superiority and effectiveness of the process monitoring method based on MIFE are fully verified.

Table 4 Fault failure alarm rates of TE process

Table 5 Fault false alarm rates of TE process

4.Conclusions

Traditional monitoring methods often perform poor when monitoring the simultaneous nonlinear and non-Gauss process data.They present large false alarm rate and failure alarm rate,which seriously affect the decision-making process of chemical production.In this paper,a MIFE monitoring method is proposed to overcome the shortcomings of the traditional algorithm.The method first uses MI to select the feature subset to replace the traditional linear correlation detection method.Its main contribution is that the whitening variable subset can better maintain the original data cluster structure information,reducing the number of variable detection and redundant alarms.For PCA,only the linear relationship between variables can be reflected,and the nonlinear relationship cannot be measured effectively.For MIFE,after data is selected by the characteristics of mutual information,the correlation between the original nonlinear variables is removed and the PCA method is extended to the nonlinear domain,which makes up for the linear limitation of the PCA method when extracting the data features.In addition,MIFE based dynamic modeling method provides a feasible solution for chemical process monitoring with certain practical value.