Department of Chemistry and Chemical Engineering,South China University of Technology,Guangzhou 510640,China

Keywords:Supercritical carbon dioxide extraction Pogostemon cablin Response surface methodology Mathematical modeling Simulated annealing algorithm

ABSTRACT The supercritical carbon dioxide extraction was applied to obtain essential oil from Pogostemon cablin in this work.Effect of extraction parameters including temperature,pressure,extraction time and particle size on extraction yield was investigated,and the response surface methodology with a Box-Behnken Design was used to achieve the optimized extraction conditions.The maximum yield of essential oil was 2.4356%under the conditions of extraction temperature 47°C,pressure 24.5 MPa and extraction time 119 min.Moreover,based on the Brunauer-Emmett-Teller theory of adsorption,a mathematical modeling was performed to correlate the measured data.The model shows a function relationship between extraction yield and time by a simple equation with three significantly adjustable parameters.These model parameters have been optimized through simulated annealing algorithm.The predicted data from the mathematical model show a good agreement with the experimental data of the different extraction parameters.

1.Introduction

Pogostemon cablin(patchouli)belongs to the Lamiaceae family and it is an herbal plant from Philippines,Iran,Indonesia,China,etc.[1-3].In Chinese ancient history,patchouli has been used to treat various diseases[4].Patchouli oil is extracted from the stems,leaves and flowers of patchouli.Extracts from this plant contain numerous components including terpenes,alcohols,ketones,and acids[5].It is well known that essential oil from P.cablin has pleasant flavoring,medicinal,antimicrobial and antioxidant properties.Therefore,it is extensively applied for the food and cosmetics industry[2,3].It can be also suitable for use as medicine to treat rheumatism,headache,cold,vomiting,diarrhea,abdominal pain and wounds[3,6]and as antimicrobial agent to keep away Gram-positive bacteria[7]and Staphylococcus aureus[8].

Different extraction methods have a certain effect on the quality of essential oils.The patchouli oil has frequently been extracted by hydro-distillation(HD)[1]or solvent extraction.However,the method of HD requires high temperature,which has many disadvantages such as high cost,thermal degradation of heat-sensitive compounds,long extraction time,and low yield[9].Moreover,solvent extraction method can cause environmental pollution,and damage these sensitive compounds[10].

In recent years,supercritical carbon dioxide(scCO2)extraction has been deemed as a promising separation method of the various industrial areas such as recovery and separating extracts from natural products[11-14].The singular physicochemical properties of carbon dioxide are having low critical temperature(31.1 °C)and pressure(7.38 MPa).Carbon dioxide is non-toxic,inert,not oxidant and easy to be recycled from the extracted natural product[15,16].When compared to other extraction methods,scCO2extraction has many advantages such as low operating temperatures to reduce energy consumption,preservation of heat-sensitive compounds and avoidance of residual toxic solvent.Moreover,scCO2extraction maintains the organoleptic features of the natural plants,and it is better than the conventional extraction techniques[17].

The efficiency of scCO2extraction relies on several significant factors such as extraction temperature,pressure,particle size,and extraction time.The response surface methodology(RSM)with a Box-Behnken Design(BBD)has been proved to be a powerful statistical and mathematical approach to analyze the effect of several variables on one or more responses,and optimize these factors for the largest target value[18-21].Recently,the RSM has been successfully applied to optimize extraction of essential oil from Laurus nobilis[22],caraway[23],lavender[24],orange peel[25],Cyperus rotundus[25],geranium[26]and valerian roots[27].

Mathematical modeling on the supercritical extraction process is a significant tool for optimizing and scaling laboratory data up to industrial standard and to assess the impact of operation parameters on the economic and technical practicability of industrial processes[28,29].Furthermore,mathematical model has become a key step for the exploitation of extraction process,because it can be applied to design industrial equipment,which can enormously decrease a number of experiments in the laboratory[30].According to many literatures[30-34],several models have been developed to simulate the supercritical fluid extraction of essential oil.Due to the different mechanisms of mass transfer,these models can be divided into four major categories:empirical models[35],shrinking-core models[36],models based on heat transfer analogies[37]and models based on differential mass balance[38].Compared with other models,model based on differential mass balance has a mass of advantages such as less thermodynamic parameters and better mechanism expression of mass transfer for the extraction process.

With the increase of computing power,many complex mathematical models of supercritical fluid process have been solved by some intelligence algorithms such as simulated annealing(SA)[39],genetic algorithm(GA)[40],particle swarm optimization(PSO)[41],differential evolution(DE)[42],ant colony algorithm(ACA)[43],Levenberg-Marquardt(L-M)[44]and taboo search(TS)[45].

The first aim of this research is to study the influence of the extraction variables such as pressure,temperature,particle size and extraction time on the extraction yield of patchouli oil by using RSM with a BBD.Secondly,this work aims to apply the mathematical modeling by the differential mass balance methods to correlate the experimental data of scCO2extraction.Finally,the adjustable parameters of this model have been optimized by SA algorithm.The overall research framework of this paper was shown in Fig.1.

2.Materials and Methods

2.1.Materials and chemicals

The stem and leaves of P.cablin in this study were purchased from a local herbal medicine market in Guangzhou,China.Carbon dioxide(≥99.99%)was obtained from Guangzhou Shengying Gas Co.,Ltd.All chemical regents were of analytical grade.

2.2.Sample preparation

The stem and leaves of P.cablin were dried in an electrothermostatic blast oven(type DHG-9240,Shanghai Shenxian Constant Temperature Equipment Factory)until all the free water was removed.The dehydrated samples were smashed by a high speed pulverizer(type QE-100,Zhejiang Shengli Industry and Trade Co.,Ltd.)and then separated from the required particle size using a kit Sieve Shaker.Treated samples were loaded into a storage box,kept away from light and stored at room temperature before using.

2.3.Methods

2.3.1.Hydro-distillation

According to Chinese pharmacopeia,the dried sample(50 g)of P.cablin was hydro-distilled by using an all-glass extraction apparatus for 3 h.After extracted,the patchouli oil was dehydrated by using anhydrous sodium sulfate,then weighed and stored in a refrigerator at 4°C.Each experiment was repeated three times.The yield of patchouli oil was 0.6235%(w/w)with application of the hydro-distillation method.

2.3.2.Supercritical carbon dioxide extraction

The experimental apparatus of scCO2extraction was illustrated schematically in Fig.2.The dehydrated samples(120 g)of P.cablin were added into the stainless steel extractor,with steel wool placed at its bottom and top to prevent patchouli particles from blocking the pipeline.The temperature is controlled by a strip heater around the extractor and measured by a thermocouple.The pressure and flow rate of CO2were adjusted accurately by the micro-metering valve,respectively.In this work,the flow rate of CO2was invariably maintained at 20 L·h-1.The static time was 30 min for all experiments,which was incorporated in total extraction time.The dynamic time was ranged from 30 min to 150 min.Additionally,in order to obtain high quality essential oils,the extraction process was conducted by using two separators.Both separators'temperatures were constant at 30°C,while the pressure was separately kept at 10 MPa and 6 MPa according to the sequence of the two splitters in Fig.2.The operation steps were as follows:Firstly,carbon dioxide from a gas cylinder was introduced to a refrigerated container and then turned into liquid CO2by cooling;Secondly,the liquefied CO2was pressurized by a high pressure pump and then passed into the whole extraction device.Finally,patchouli oil was extracted by adjusting the relative parameters of the temperature,pressure,particle size,and extraction time.The extracted essential oil was weighed after collection and then the essential oil yield can be calculated through dividing the mass of essential oil by the mass of P.cablin powder fed into the extractor.

2.3.3.Gas chromatography analysis

Fig.1.Flow chart of extraction essential oil and mathematical modeling.

Fig.2.Schematic diagram of scCO2extraction equipment:1—CO2cylinder;2—on-off valve;3—CO2pump;4—pressure gauge;5—CO2vessel;6—extraction vessel;7—heat jacket;8—manual back pressure regulator;9—separator;10—safety valve;11—CO2pump chiller.

The compositions of essential oil were identified and analyzed by using a gas chromatograph(GC 6820,Agilent Technologies)equipped with a flame ionization detector(FID)and a HP-5MS 5%phenyl methyl siloxane capillary column(30 m×0.32 mm×0.50 μm).The temperatures of the injection and the flame ionization detector were set at 250°C and 280°C,respectively.The column temperature was programmed as follows:the initial temperature 60°C for 2 min,then subsequently increased at the speed of 3°C·min-1from 60°C to 280°C and held constant at 280°C for 5 min.The carrier gas was helium with a speed of 1.0 ml·min-1around the column and the injected sample volume was 1 μl of the patchouli oil with the spilt ratio of 1:100.The mass spectrometry(MS 5977B,Agilent Technologies)parameters were:electron energy 70 eV;ion source temperature 230°C;electron multiplier voltage 0.74 kV;acquisition mass range m/z 40-450;scan rate,5 scan·s-1;and solvent delay 3 min.The components of patchouli oil were authenticated by comparison of their linear retention indices(LRIs)on the two columns,determined in relation to a homologous series of n-alkanes,with those from pure standards or reported in literature,as well as comparison of fragmentation patterns in the mass spectra with those stored on the GC-MS library[46].

2.4.Experimental design

In this work,single-factor experiments were carried out to evaluate the influence of extraction variables such as temperature,pressure,particle size,and extraction time.It is well-known that this method can provide a reasonable range of data for the RSM.In the single-factor experiments,the yield response(Y)is only a function of the variable ratio(xi)and not of its total quantity.The obtained scCO2extraction experimental data and essential oil yield according to the single-factor experiment were shown in Fig.3,and all errors of these yields were less than 0.003%.Additionally,the RSM was employed to optimize experimental parameters for extracting essential oil from P.cablin.According to the result of the single-factor experiment,three factors consisting of temperature(x1),pressure(x2),extraction time(x3)as independent variables were selected and the correlation of three independent variables by using the BBD was evaluated.The BBD is an effective template for RSM,a type of rotatable and three-level incomplete factorial designs for correlating a second-order response surface.The completed design consisted of 17 experiments that incorporated two repetitions of the central point and 12 factor points.Table 1 illustrates the homologous uncoded levels of the independent and coded by using the RSM design.According to the BBD,the independent variables and the relevant experimental yields were listed in Table 2.The experimental data were analyzed by BBD to fit a second-order polynomial equation as follows:

Fig.3.The effect of the independent variables on the yield of extracted oil.

Table 1 Coded and uncoded levels of independent variables used in the BBD

Table 2 Box-Behnken Design with coded and uncoded levels of independent variables,and experimental yields

where Y is the yield of patchouli oil;β0,βi,βiiand βijare fitting parameters;and xiand xjare the coded degrees of independent variables.The importance of regression coefficients was assessed by applying analysis of variance(ANOVA).The determined coefficient(R2)and its adjusted value(adj.R2)were applied to estimate the consistency of the simulation results and the experimental data.

2.5.Mathematical modeling

2.5.1.Fixed bed extraction modeling

Fig.4 shows a packed bed of P.cablin powder as the solid phase and the flowing scCO2as the liquid phase.Based on the general model for the supercritical fluid extraction of a solid substrate in the packed bed,the differential mass balance equation was applied to describe the extraction process,and can be defined as[47]:

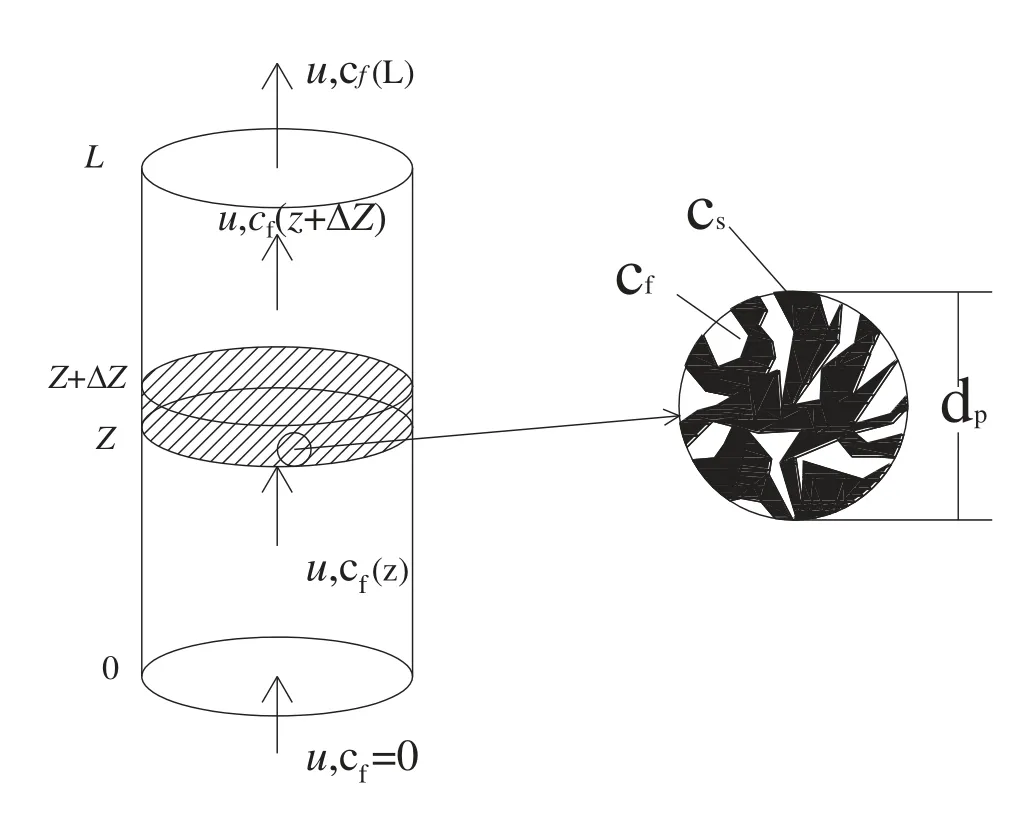
Fig.4.Schematic diagram of the extraction vessel.

Here,Cfrepresents the concentration of the solute in the scCO2;u is the interstitial velocity of the scCO2;ε is the porosity of material bed layer;Dsfrepresents the axial dispersion coefficient of the solute in the scCO2;asfis the effective solid-fluid contact area for mass transfer;and ksfis the mass transfer coefficient for carriage of the solute pass through the external fluid membrane around the solid particles,and Cf∗is the concentration of solute in the scCO2membrane at equilibrium with the solid surface.The differential mass balance equation can be predigested according to the method applied by Pardo-Castaño et al.[48].Therefore,the simplified assumption of the mathematical model was proposed as follows:(a)the internal temperature and pressure of the extractor are evenly distributed.Therefore,the dissolution and diffusion process of the solute is carried out at the same temperature and pressure;(b)the axial diffusion is ignored in the extraction process because the length of the extractor is at least 50 times to the average diameter of particle and the Reynolds number is greater than 10[49];(c)the particle porosity and bed voidage are constant and do not change in the extraction process;(d)there is local equilibrium at interface of fluid and solid phase,which was quickly reached[3,50];(e)the variation of solute in differential thin layer(ΔZ)in comparison with the variation of the height accumulation is negligible;(f)the mathematical model is single dimensional and only considered the vertical coordinates;and(g)the solute is considered as a pseudo-component,and the concentration of solute in the supercritical fluid has not a gradient in the radial directions.Thus,the differential mass balance equation is simplified to the following equation:

where y is the mass fraction of the solute in the scCO2and yeis the solute mass fraction in the scCO2film with the solid surface at equilibrium.

Integrated Eq.(4)within the usual boundary conditions for a packed extractor(z→0,y→0 and z→L,y→yL),the equation was obtained as follows:

where k=(1-ε)asfksf,and yLrepresents the mass fraction of solute in the bulk fluid phase at the exit of the extractor;L is the height of extractor.The external mass transfer coefficient ksfwas defined by applying the following equation[50]:

The Sherwood number(Sh)can be calculated by two related functions of the Reynolds number(Re)and Schmidt number(Sc)given by:

(1):Re(0.26-1.90)and Sc(7.24-21.93)[51]

(1):Re(2-40)and Sc(2-40)[52]

The dimensionless parameters(Re,Sc and Sh)were obtained by the following equations:

where D represents the diffusion coefficient of solute;ρ is the density of the solvent;and dpand μ represent the particle size and the viscosity,individually.

Besides Eq.(5),it is necessary to establish the material balance of the solute in the solid expressed by:

in which msrepresents the mass of solute in the solid;q is the mass flow rate of the scCO2;and mLand msolvrepresent the mass of solute and solvent in the scCO2at the outlet of the extraction vessel,separately.

In addition,Eq.(12)can be also described in mass fraction as:

Pardo-Castaño et al.[48]proposed that Eq.(13)could be simplified when yLmeets the condition(yL≪1).However,owing to the high solubility of the patchouli oil in the scCO2,Eq.(13)was solved as presented.

In this work,in order to premeditate the solute interaction with the solid matrix,a BET-type equilibrium relationship for scCO2extraction processes was applied.The equation was given as follows:

in which χ represents the ratio of the mass fraction to solute at equilibrium(ye)and the mass fraction solute in a saturated scCO2phase(ysat);xsrefers to the solute mass fraction in the solid at the time of t;xmis the mass fraction of solute in the first monolayer(mm/mo),where mois the initial mass of the solute in the packed bed,and K represents ratio of the adsorption equilibrium constants of the solute in the first monolayer to that in subsequent layer.

By solving Eq.(14),the following equation can be obtained:

At last,Eq.(15)is applied in Eq.(5)with ym=χysat.Eq.(13)is a differential equation with three adjustable parameters(xm,ysat,K),which was solved by applying the ode45 subroutine in MATLAB.

The average absolute relative deviation(AARD)as defined in Eq.(16)was usually applied to evaluate the agreement between the calculated yields and the experimental yields.

in which n denotes the number of experimental data;Yi,caland Yi,expare the essential oil yields of extraction obtained by the calculated model and the experimental data,separately.

2.5.2.Simulated annealing

SA based on the principle of statistical mechanics was introduced by Kirkpatrick et al.,which is an effective global optimization algorithm[53,54].This optimization algorithm has been widely applied to solve complex nonlinear function problems[55,56].In condensed matter physics,annealing describes a physical process that a solid is heated in order to maximize the temperature at which all molecules are randomly distributed in the liquid phase,and then the temperature of the solid is slowly dropped until the emergence of an immaculate crystal.Due to the formation of this crystal,the mechanical structure has been improved.The SA algorithm applies homologous“temperature drops”process for many nonphysical optimization problems.In the optimization process,the arrangement of the low energy bonds at the heating stages is the fitness function of the optimization problem.The controlled cooling process is the optimization process itself.At each iteration step,the temperature is assumed to decrease so that a low energy bond of the atoms is assumed.Within the iteration steps,the algorithm searches the neighbors of the current solution for a better solution.The iterative process is repeated until a more appropriate solution is found.This algorithm process mainly includes four parts:cold work,recovery,recrystallization and grain growth[57].A simplified flowchart of SA algorithm is shown in Fig.5.

Fig.5.Flow chart of simulated annealing optimization algorithm.

The SA algorithm is implemented as follows:

(1)The algorithm gives a set of random initial parameters and then the objective function(E0)is calculated.

(2)The algorithm generates the new random parameters,then the new objective function(E1)is calculated and obtained ΔE=E1-E0.

(3)If ΔE≤0,the new random parameters will be accepted;otherwise,the new random parameters will be accepted with probability exp(-ΔE/T).

(4)If the criterion of the step(3)is satisfied,the algorithm will store systematically the best random parameters;otherwise,it will go to step(2).

(5)Eventually,if the algorithm has reached the terminating condition,the optimal solution is given and the program is finished.

In this work,the adjustable parameters of the mathematical model were obtained by using SA algorithm,which could reduce the error between the experimental data and model results.

3.Results and Discussion

3.1.Comparison of composition and yield at different methods

In this work,the GC-MS analysis was applied to estimate the quality and identify the chemical compositions of patchouli oil obtained by the HD and scCO2methods.The chemical compositions of patchouli oil were listed in Table 3.It provided the compositions of patchouli oil according to peak area percentage of each compound.Shown from Table 3,the chemical compositions of patchouli oil from scCO2extraction were obviously different from HD extraction.The number of compounds by using scCO2extraction is more than that by the hydrodistillation,and the concentration of each compound has some discrepancy.However,the main compounds in patchouli oil from both extraction methods are α-Guaiene,seychellene,longifolenaldehyde,patchouli alcohol,and pogostone.The yields obtained from the scCO2under the optimized conditions and hydro-distillation methods were 2.4356%(w/w)and 0.6235%(w/w),respectively,and the extraction yield of scCO2was obviously higher than that of the hydro-distillation method.This indicates that the scCO2extraction can be carried out more effectively than the HD.

3.2.Single factor experiments

The extraction conditions have a great influence on the yield of patchouli oil.Single factor experiments about the effect of temperature(40-60°C),pressure(10-30 MPa),particle size(0.2-1.0 mm),and extraction time(30-150 min)on the yield of essential oil were studied.The primary influences of the extraction conditions on the yield of essential oil have been shown in Fig.3.According to this figure,the yield of essential oil was increased at the extraction temperature from 40°C to 45°C.The yield of essential oil was decreased when the temperature is higher than 45°C.The effect of temperature of scCO2on the extraction yield is manifested at two aspects:the rising temperature increases the diffusion coefficient of the solute,which leads to the increasing of the yield of essential oil.On the other hand,the temperature rise causes a reduction of the CO2fluid density,then the solubility of solute in the CO2fluid decreases and the yield of essential oil goes down[58,59].Therefore,the extraction temperature was chosen between 40°C and 50 °C at the following experiments of RSM.Moreover,it can be seen that the yield of essential oil has obviously gone up at the increase of extraction pressure from 10 to 25 MPa,which depends on the increase ofthe scCO2density.As expected,the increase of scCO2density causes an enhancement in the solubility of the essential oil with the scCO2fluid[60,61].However,the extraction pressure considered has a weak influence on the yield of essential oil when the pressure is more than 25 MPa.The density of scCO2is higher as pressure is higher,but the diffusion of carbon dioxide and the rate of mass transfer are weakened.Furthermore,higher extraction pressure will increase equipment losses and the costs of equipment operation and maintenance.So the extraction pressure was set from 15 and 25 MPa at the following research of RSM.

Table 3 Chemical compositions of patchouli oil extracted by the HD and scCO2extraction methods

As shown in Fig.3,the yield of patchouli oil gradually increased with the increase of extraction time less than 90 min.When the extraction time was more than 90 min,the yield curve of essential oil has gently changed.Because shortening the extraction time means saving energy consumption,the extraction time was set between 60 and 120 min.Moreover,as the particle size of the P.cablin enlarges,the yield of essential oil changes very weakly relative to other extraction parameters.Hence,in the following response surface analysis,research on the effect of temperature,pressure and extraction time on the yield of essential oil was carried on.

3.3.Prediction and optimization using RSM

According to the results of the single-factor experiments,the influence of three extraction parameters of scCO2,namely temperature(40-50°C,x1),pressure(15-25 MPa,x2)and time(90-120 min,x3),on the maximum yield of essential oil from P.cablin were studied by applying the RSM with BBD.The experimental results were given in Table 2.The analysis of variance(ANOVA)was applied to estimate the significance of the regression coefficients of the RSM,which have a negative or a positive influence on the yield of patchouli oil from P.cablin.The ANOVA for the RSM of scCO2extraction parameters was provided in Table 4.The F and p values were applied to determine the importance of each coefficient and also show the interaction strength between the independent variables.The higher F-value and lower p-value demonstrated more significance of the relevant coefficient.The high model Fvalue(F=29.89)and low p-value(p＜0.0001)indicated that the response surface model was highly statistically significant.Moreover,the lack-of-fit(＜0.0001)estimates the success of the model to experimental data.The coefficient of determination(R2)and adjusted coefficient of determination(R2adj.)were 0.9746 and 0.9420,respectively.It showed a good agreement between the experimental yields and the predicted yields.In addition,the low value of the coefficient variation(CV=2.31%)indicated that the experiments were reliable.Fig.6 presents the relationship between the experimental results and the computed yields from RSM,which is used to assess the reliability of this model.Seen from Fig.6,the experimental results are well fitted by theRSM.The results were presented in Table 4 and it demonstrated that effect of all linear terms and quadratic terms(x1×x1)on the yield of essential oil is highly significant(p＜0.01).The interaction terms(x1×x2)and quadratic terms(x2×x2)were significant(p＜0.05).However,the other terms were insignificantly influential(p＞0.05).All linear terms,the interaction terms(x1×x2),(x1×x3)and quadratic terms(x3×x3)have a positive effect on the yield of essential oil.The other two individual parameters perform a negative influence on the yield of extraction.The full quadratic Eq.(2)was fitted by involving the yield of essential oil,and the fitting equation is as follows:

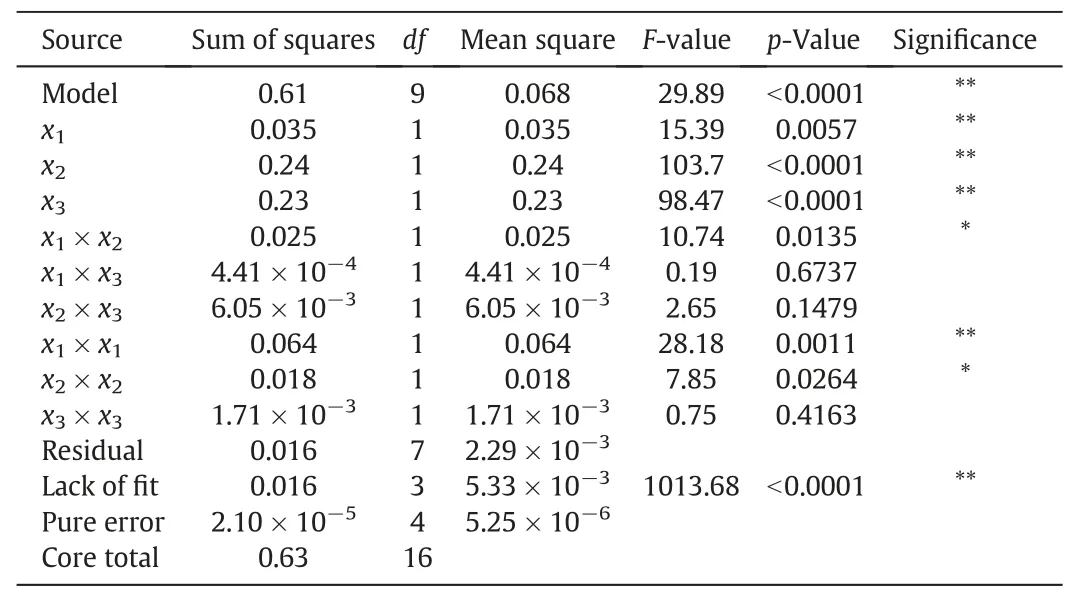
Table 4 Analysis of variance(ANOVA)and response surface model adequacy for the yield of patchouli oil

Fig.6.The degree of agreement between the experimental and predicted yields by using RSM.

The response surface graph is a three-dimensional(3D)response surface,which indicates the single and multi-dimensional influence of extraction parameters on the yield of essential oil.According to this regression model,the yield of essential oil in relation to the temperature,pressure and time was shown in Fig.7a-c.The three-dimensional response surface plot of effect of temperature and pressure on the yield of essential oil was shown in Fig.7a.From Fig.7a,the yield of essential oil was increased with the increase of extraction pressure from 15 to 25 MPa,and pressure had positive effects on the yield of essential oil.The yields of essential oil were obviously improved with the increase of pressure,because increasing pressure could increase the density of CO2and enhance the solubility of the essential oil in the scCO2fluid.Additionally,when the extraction temperature was changed,the yield of essential oils showed a tendency towards increasing firstly and then decreasing in Fig.7a.

Effect of temperature and time on the yield of essential oil was demonstrated in Fig.7b.It can be seen that extraction time has a positive influence on the yield of essential oil,and the influence of temperature is similar to that of Fig.7a.According to the three-dimensional response surface plot and the result of BBD,effect of interaction between temperature and time on extraction yield is insignificant.Fig.7c describes the three-dimensional response surface plot of the yield as a function of the pressure and time at 45°C.As shown in Fig.7c,the yield of essential oil was obviously increased with the increase of pressure from 15 to 25 MPa and time from 60 to 120 min,which indicated that pressure and time have a highly significant influence on the yield of essential oil.However,the interaction effect between the pressure and time on essential yield is not significant.Generally,extracting at the optimized extraction parameters can not only highly increase the yield of essential oil but also reduce the operation cost.In this work,the maximum yield of essential oil obtained by scCO2was at temperature 48°C,pressure 24 MPa and time 119 min.The maximum yield of essential oil obtained by the model is 2.4370%(w/w).The experimental yield of essential oil under the theoretical optimized conditions was 2.4356%(w/w).The experimental result is almost similar to the theoretical yield of essential oil,which indicates that the model can be well used to optimize the extraction conditions of essential oil.

3.4.Mathematical modeling results

The mathematical modeling was widely applied to estimate the scCO2extraction process of natural product[48,61,62].In this study,the mathematical modeling can be used to fit the experimental results.The SA algorithm for the nonlinear optimization was carried out through MATLAB program.For solving model equations in this study,many empirical important parameters were experimentally obtained and shown in Table 5.Table 6 gives the experimental operation conditions.The diffusion coefficient of solute in the scCO2,the external mass transfer coefficients,and the dimensionless parameters were also listed in Table 6.The solvent viscosity and density under a wide variety of extraction conditions can be obtained from NIST chemistry webbook in operational conditions(http://webbook.nist.gov/chemistry/).According to the results in Table 6,Re is greater than 10 for all experimental conditions.Table 7 and Figs.8-9 demonstrated that the correlated results of the BET based model were compared with the experimental values for the scCO2extraction under different conditions.

The model equations have three significant adjustable parameters:xm,K and ysatoptimized by minimizing the sum of square errors between experimental data and model fitting values.The AARD was shown in Table 7.As demonstrated in Table 7,all the AARD values are no greater than 2.02%,which indicated the mathematical modeling gives good representation for the scCO2extraction of essential oil from P.cablin.Thus,Figs.8 and 9 also demonstrate a good agreement of the experimental data with the fitted data from the mathematical model.Determining the initial value of the adjustable parameters is a key step in the simulation solution process.The values of xmare in inherent attribute of the solid-solute interaction,which is not affected by temperature and pressure.Therefore,xmis a constant in various extraction conditions.Because the initial mass of transferable solute is more than the mass of solute in the first monolayer,the xmvalue is less than 1[3,48,50].Seen from Table 7,the value of ysatincreases with the enhancement of pressure(15-25 MPa)and K value is decreased obviously at the certain temperature.Since the value of ysatis positively correlated to solubility,the molecular forces of solid-solute become quite weaker when solubility of the solute in the scCO2increases,which would cause the K values to decrease.These results have been similarly reported by otherreferences[3,48,50].Fig.8 gives the comparison of experimental data and calculated results using the mathematical modeling for the scCO2extraction at 45°C and 15-25 MPa,where the three stages can be premeditated.It can be clearly shown in Fig.8 that the BET based model can accurately correlate the experimental data for the extraction of essential oil and obtain the highest yield under the condition of 45 °C and 25 MPa.The three stages can be demonstrated by the curve of scCO2extraction at the pressure of 15-25 MPa.The first phase of the curve slope is stable,which indicates the stage with a constant extraction rate.And then the slope of the curve slows down,the second phase indicates a falling extraction rate.At last,the third phase declares diffusion control which is slow and the commanding extraction theory.In this study,because the third phase of kinetics is difficult to implement through experiment,it was not markedly demonstrated.The third phase of kinetics also was not achieved in other literatures[3,63,64].Fig.9 is the comparison of experimental data and calculated results using the mathematical modeling for the scCO2extraction at 20 MPa and 40-50 °C,and the highest yield of essential oil was determined under the condition of 45°C and 20 MPa.The mathematical modeling should be considered as a promising method to evaluate the kinetic process of the scCO2extraction of essential oil from P.cablin.

Fig.9.Comparison of experimental data and calculated results using the mathematical modeling at P=20 MPa,dp=0.6 mm.

4.Conclusions

In this work,the scCO2extraction and hydro-distillation were applied to obtain the essential oil from P.cablin,and chemical composition of essential oil from both methods was compared by GC-MS analysis.The single-factor experiments studied the influence of temperature,pressure,extraction time and particle size on the scCO2extraction of patchouli oil.The RSM-BBD was employed to optimize the extraction factors on the basis of a single-factor experiment.The maximum yield of patchouli oil obtained by scCO2was 2.4356%under the optimized conditions of temperature 47 °C,pressure 24.5 MPa and extraction time 119 min.The BET-based mathematical model has successfully been applied to describe the scCO2extraction.The SA algorithm was used to obtain the three significant adjustable parameters of the model.The AARD values are less than 2.02%,which indicates the mathematical modeling has a satisfactory good performance and can be applied to correlate experimental data.Namely,the mathematical modeling is a promising method to evaluate the kinetic process of the scCO2extraction of essential oil from P.cablin.

Nomenclature

AARD average absolute relative deviation

asfimpactful solid-fluid contact area

Cfconcentration of the solute in the scCO2

Cf∗concentration of solute in the scCO2membrane that is in equilibrium with the solid surface

D diffusion coefficient of the solute

Dsfaxial dispersion coefficient of the solute in the scCO2

dmdiameter of the extractor

dpparticle size

K ratio between the adsorption equilibrium constants of the solute in the first monolayer and that in subsequent layers

ksfmass transfer coefficient for carriage of the solute pass through the external fluid membrane around the solid particles

L length of the extractor

mLmass of solute in the scCO2at the export of the extractor

moinitial mass of the solute in the packed bed

msmass of solute in the solid

msolvmass of solvent in the scCO2at the export of the extractor

q mass flow rate of the scCO2

Re Reynolds number

Sc Schmidt number

Sh Sherwood number

u interstitial velocity of the scCO2

xmmass fraction of solute in the first monolayer(mm/mo)

xsmass fraction of solute in the solid at time t

yemass fraction of solute in the scCO2film that is in equilibrium with the solid surface

yLmass fraction of solute in the bulk fluid phase at the exit of the extractor

ysatmass fraction of solute in a saturated scCO2phase

ε porosity of material bed layer

μ viscosity

ρ density of the solvent

ρsdensity of the solid phase