赵春娥，程志远，谭尊林

(中国石油大学(华东) 理学院,山东 青岛 266580)

群的概念已经普遍地被认为是数学及其许多应用中最基本的概念之一，它不但渗透到如几何学、函数论、泛函分析等许多数学分支中，还在其他领域如结晶学、理论物理、量子化学、代数编码学、自动机理论等方面都有重要的应用.

论文主要将群的理论应用于多址联接通信技术中.多址联接通信技术在移动通信网和卫星通信网等工程领域都有广泛的应用，主要有频分多址、时分多址和码分多址3种基本多址技术.时分多址是把时间分割成互不重叠的时段(帧)，再将帧分割成互不重叠的与用户具有一一对应关系的时隙(信道).当多个用户在同一时隙通信的时候，为了避免因冲突的产生使得发送消息不能被基站接收而导致通信失败，每一个用户都指定了一个通信协议，用户按照协议来进行通信.而每一个通信协议都是由一个冲突可避码的码字作为支撑集生成的0-1序列.因此，成功完成通信的基本保障是构造合适的冲突可避码.在这里，冲突可避码的重量w是可以同时进行通信的用户数目，码的容量为系统所支持的通信用户的总数.

对于重量w=3的冲突可避码， 文献[1-5]在长度为n=16m，n=4(mod8)，n=4m，n=2(mod4)，n=1(mod2)时，给出了相应的最优冲突可避码的构造方法.文献[6]给出了奇素数长紧的等差码存在的充要条件并给出了最优等差码冲突可避码的直接构造和递归构造.文献[7]给出了奇数长冲突可避码容量的上界.对于重量w=4，文献[8-9]分别利用了有向图和无向图，给出长度为2a3b和2a3bm的最优冲突可避码的分析和构造.对于一般重量w，文献[10]给出了常重量冲突可避码的上界，文献[11]给出了渐进上界和最优构造方法.论文将对文献[12]中的方法进行推广，得到更多满足条件的素数p，从而构造更多长度的最优码，可以给更多的用户提供协议序列进行通信，提高通信系统的性能.

1 预备知识

d*(I)={j-i|i,j∈I,i≠j},

其中：减法是指模L的减法运算.

一个长为L、重量为w的冲突可避码(conflict-avoiding code，简称CAC)C是P(L,w)的一个满足下面条件的子集

d*(Ij)∩d*(Ik)=φ，∀Ij,Ik∈C,j≠k,

其中：每一个I∈C都称为一个长为L、重量为w的码字.

一个码字I∈P(L,w)称为是等差的，如果I中每一个元素都形成ZL的一个等差排列，即

I=(0,i,2i,…,(w-1)i)，对于某个i∈ZL.

在上面的式子中，乘积是指模L的乘法运算，i被称为这个码字的生成元，差的集合等于

d*(I)=(±i,±2i,…,±(w-1)i).

如果一个冲突可避码C中所有的码字都是等差的，则称C是等差的，并且其生成元的集合记为Γ(C).

对于一个给定的L，令CAC(L,w)是所有的长为L、重量为w的CAC的集合.某个码C∈CAC(L,w)具有极大容量，则记其容量为M(L,w)，即

M(L,w)=max{|C||C∈CAC(L,w)}.

类似地，令CACe(L,w)是长度为L、重量为w的等差CAC的集合，等差码C∈CACe(L,w)的极大容量记为Me(L,w)，即

Me(L,w)=max{|C||C∈CACe(L,w)}.

对于一个等差码C∈CACe(L,w)，如果

|C|=Me(L,w)，

则称C是最优的.一个最优的码C∈CAC(L,w)，如果

则称C为紧的.

2 常重量素数长冲突可避码的最优构造

定义1[12]给定素数p，令

Zp={0,1,…,p-1}，

则Zp中的非零元集合Zp*对于模p的乘法运算是一个阶为p-1的循环群.

对于p-1的因子f，记Zp*的f阶乘法子群为

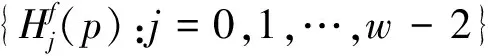
定理2令p=2(w-1)ms+1是一个素数，如果存在Zp*的2m(w-1)阶子群H，使得{1,2,…,w-1}是{Nj:j=1,2,…,w-1}的一个代表系，其中:N1是H的一个2m阶子群，Nj为N1在H中的陪集，则存在最优等差(2(w-1)ms+1,w)-冲突可避码.

证明由于H是Zp*的2m(w-1)阶子群，则存在有限域Zp的本原元α，使得

H=(αs)，

令

g=αs(w-1)，

则

N1=(g)，

有

(1)

令Γ(C)={αigj:0≤i≤s-1,0≤j≤m-1}为等差码字的生成集，由于对于每一个等差码字

I=(0,αigj,2αigj,…,(w-1)αigj)，

其差的集合为

d*(I(i,j))={±αigj,±2αigj,…,±(w-1)αigj}.

由于{1,2,…,w-1}构成N1的一个代表系，由(1)式得，对于任意两个码字I(i1,j2)，I(i2,j2)，有

d*(I(i1,j1))∩d*(I(i2,j2))=φ,(i1,j1)≠(i2,j2)，

因此，由这些等差码字构成的冲突可避码是最优的而且是紧的,由αigj:0≤i≤s-1,0≤j≤m-1生成的ms个码字构成一个等差(2(w-1)ms+1,w)-冲突可避码.

特别地，当定理2中参数s=1时，即为定理1中的构造方法.因此，定理2是定理1的一种推广.

定理3[10]设G是一个群，H是G的一个子群，A是G的一个非空子集，如果A是一个H-周期，则A能写成H的某些陪集的并.

则存在最优等差(2(w-1)ms+1,w)-冲突可避码.

H=(αs(w-1))，

则

(2)

记g=αs(w-1)，令

Γ(C)={αigj:0≤i≤s-1,0≤j≤m-1}

为等差码字的生成集， 由于对于每一个等差码字

I(i,j)=(0,αigj,2αigj,…,(w-1)αigj)，

其差的集合为

d*(I(i,j))={±αigj,±2αigj,…,±(w-1)αigj}.

由于{1,2,…,w-1}构成N0的一个代表系，由(2) 式得，对于任意两个码字I(i1,j1)，I(i2,j2),有

d*(I(i1,j1))∩d*(I(i2,j2))=φ,(i1,j1)≠(i2,j2)，

因此，由这些等差码字构成的冲突可避码是最优的而且是紧的，由αigj:0≤i≤s-1,0≤j≤m-1生成的ms个等差码字构成一个(2(w-1)ms+1,w)-冲突可避码.

特别地，当定理4中参数s=1时，即定理1中的构造方法.因此，定理4也是定理1的一种推广.

3 结束语

论文主要研究了重量为w且长度为素数p的冲突可避码的最优构造.区别于以往图论圈结构的讨论方法，论文利用子群陪集划分的方法首先确定出码字差的集合，然后再还原成码字，从而构造冲突可避码.论文将已有方法中群的代表系推广至子群的代表系，又将群的代表系推广至H-周期的代表系, 扩大了参数p的取值范围，用此方法可以构造更多最优的冲突可避码.