某类包含Hurwitz-Lerch Zeta函数的三阶积分算子
2018-12-03王小元王知人温胜男
王小元,王知人,温胜男,尹 枥
(1.燕山大学理学院,河北秦皇岛 066004)
(2.滨州学院数学系,山东滨州 256603)
1 引言
设H[a,n]为单位圆盘U={z:z∈C,|z|<1}中的解析函数类且具有如下形式为了方便,设H=H[1,1].
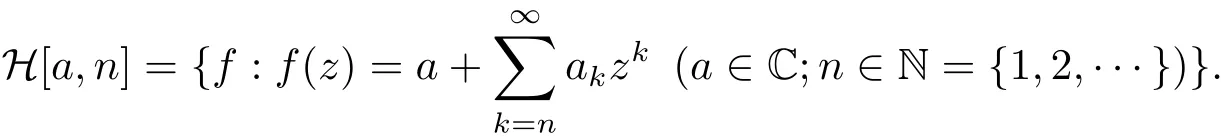
设f(z)和g(z)是U中的两个解析函数,如果存在U内解析且满足条件ω(0)=0和|ω(z)|<1的Schwarz函数,使得f(z)=g(ω(z))(z∈U)恒成立,称函数f(z)在U中从属于函数g(z),记为f(z)≺g(z).相应地,称g在U内超从属于f.下列关系

是众所周知的.更进一步地,如果g在U内单叶,则有下列等价关系
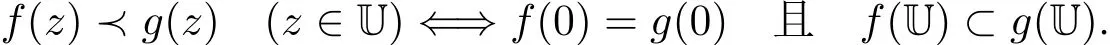
设Σ表示在去心单位开圆盘U∗={z∈C,0<|z|<1}=U{0}内解析且具有如下形式

的函数类.
下面的函数Φ(z,s,a)称为广义的Hurwitz-Lerch Zeta函数(可参考文献[1,2])

关于Hurwitz-Lerch Zeta函数Φ(z,s,a)的一些有趣的性质和特征可以参见最近的文献,例如Choi和Srivastava[3],Srivastava等[4],Lin等[5]和Garg等[6].
利用Hurwitz-Lerch Zeta函数Φ(z,s,a),Srivastava和Attiya[7](也可参考文献[8–11])引入和研究了下面的积分算子

类似于算子Js,bf(z),Wang和Shi[12]引入了积分算子

通过Hadamard卷积得到以下定义的形式

可以很容易从公式(1.1),(1.2),(1.5)和(1.6)中发现
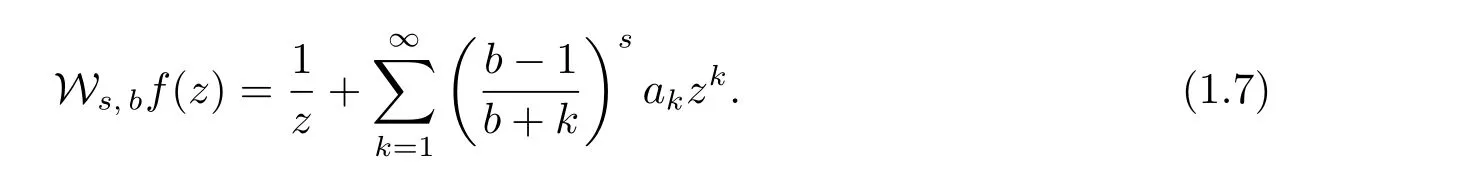
当b∈C{Z−∪{1}}时,算子Ws,b可以被定义为

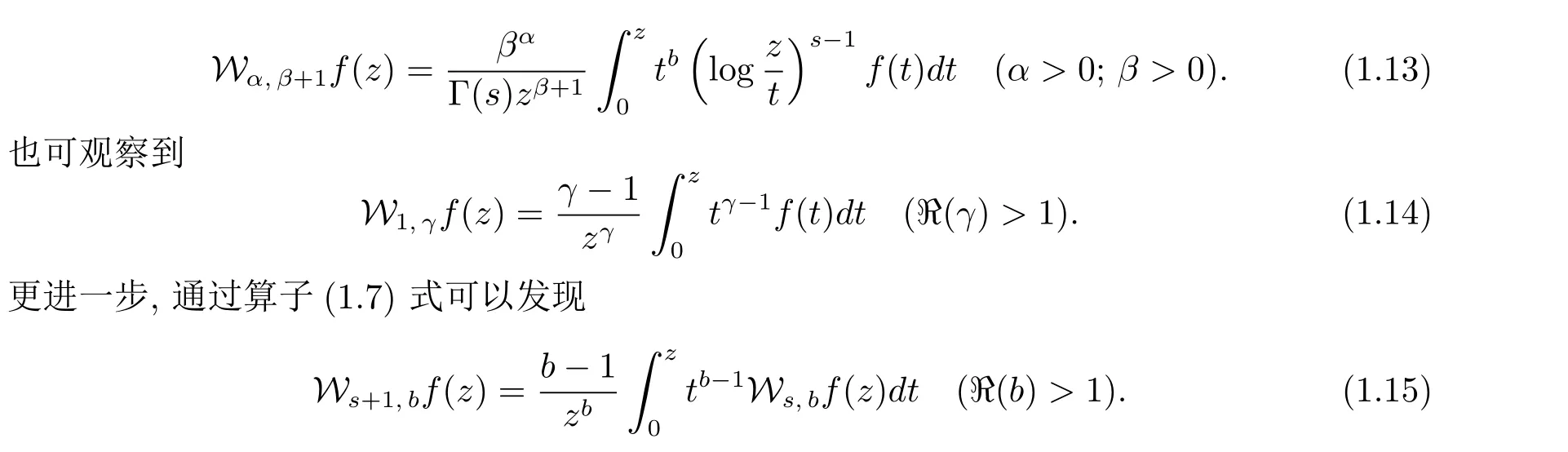
值得注意的是,算子(1.11)是被Alhindi和Darus[13]引入和研究的;算子(1.12)和(1.13)是被Lashin[14]引入和研究的.
本文的主要目的是通过研究算子Ws,bf(z)得出微分从属,微分超从属和Sandwich定理的相关结论.
2 预备知识
为了证明本文的主要结果,需要用到如下的定义和引理.
定义2.1[15]设Ψ:C4×U→C,函数q(z)和h(z)在U内单叶.若p(z)在U内解析且满足三阶微分从属条件

则称p(z)为上述微分从属的一个解.如果对所有的解p(z),有p(z)≺q(z),则称q(z)为微分从属解的一个控制.进一步,若存在一个控制eq(z)对所有适合(2.1)式的控制q(z)满足eq(z)≺q(z),则称eq(z)为最佳控制.
定义2.2[15]设Ω为U的一个子集,函数q∈Q且n∈N{1}.又设ψ:C4×U→C满足如下的允许条件
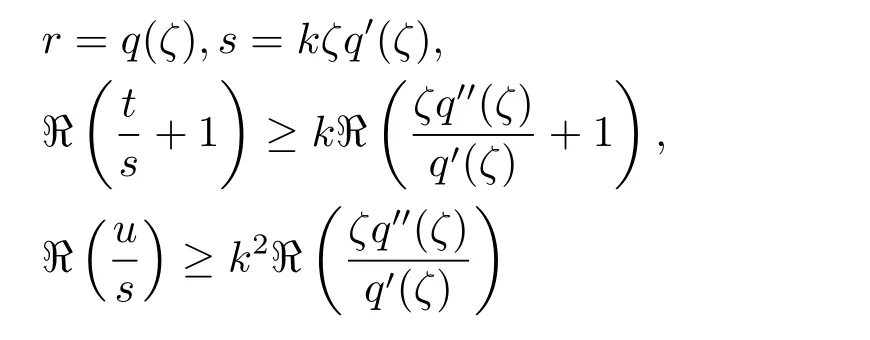
时,ψ(r,s,t,u;z)/∈Ω成立,其中z∈U;ζ∈∂UE(q)和k≥n.称上述函数ψ的集合为允许函数类,记作Ψn[Ω,q].
类似于Miller和Mocanu[16]引入的二阶微分超从属,Tang等[17]给出如下三阶微分超从属定义.
定义2.3[17]设ψ为C4×U→C的映射,函数h(z)在U内解析.如果p(z)和
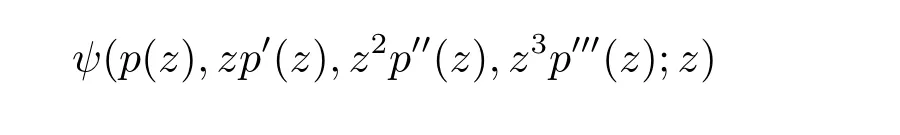
在U内单叶且满足三阶微分超从属

则称p(z)为上述微分超从属的一个解.若对所有的解p(z),有q(z)≺p(z),则称q(z)为微分超从属的一个从属子.进一步,若存在一个单叶从属子qe(z)对所有适合(2.2)式的从属子q(z),均有q(z)≺则称为最佳从属子.
定义2.4[17]设Ω为C的子集,函数q∈H[a,n]且q0(z)6=0.又设函数ψ:C4×U→C满足如下的允许条件:当

时,有ψ(r,s,t,u;z)∈Ω成立,其中z∈U,ζ∈∂U和m≥n≥2.则称上述函数ψ的集合为允许函数类,记作[Ω,q].
关于微分从属与微分超从属的条件,本文选择如下的允许函数.
定义2.5设Ω为C的子集且函数q(z)∈Q且q0(z)6=0.又设函数ψ:C4×→C满足如下的允许条件:当
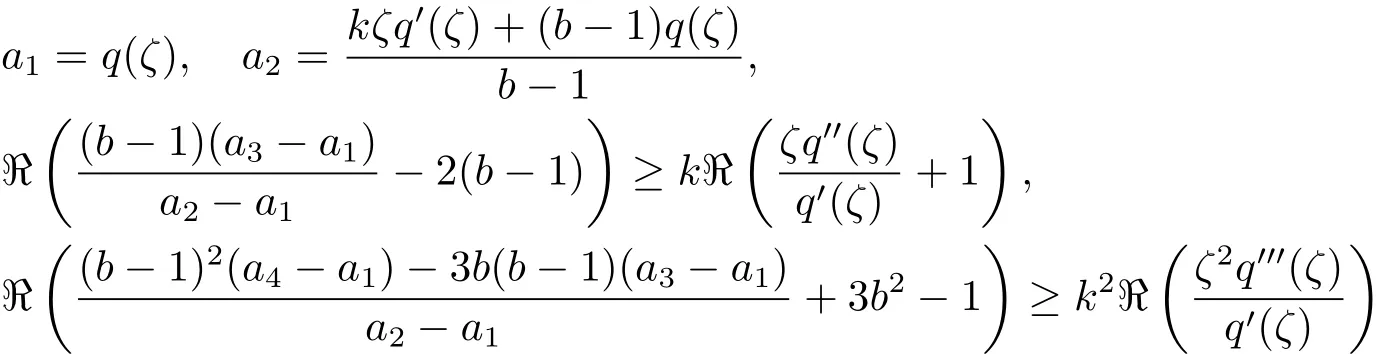
时,有φ(a1,a2,a3,a4;z)∈/Ω,其中z∈U,b∈C{∪{1}},s∈C,ζ∈∂UE(q)和k∈N{1}.则称上述函数φ的集合为允许函数,记作ΦΓ[Ω,q].
定义2.6 设Ω为C的子集且函数q(z)∈H且q0(z)6=0.又设函数ψ:C4×U→C满足如下的允许条件:当
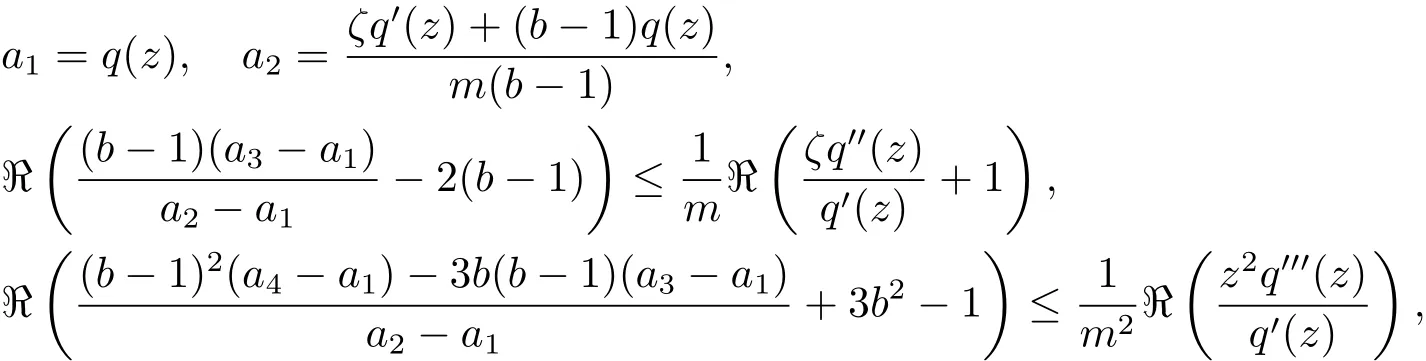
则有φ(a1,a2,a3,a4;ζ)∈ Ω,其中z ∈ U,b∈ C{∪{1}},s∈ C,ζ∈ ∂UE(q)和m ∈ N{1}.则称上述函数φ的集合为允许函数类,记作[Ω,q].
引理2.1[15]设p(z)∈H[a,n],n∈N{1},函数q(z)∈Q(a)且满足条件
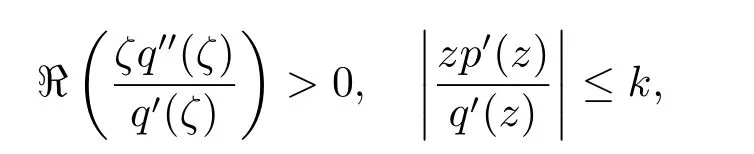
其中z∈U;ζ∈∂UE(q)且k≥n.如果Ω是C的一个子集,满足条件ψ∈Ψn[Ω,q]和

则p(z)≺q(z).
引理2.2[17]设q(z)∈H[a,n]和ψ∈[Ω,q].如果ψ(p(z),zp0(z),z2p00(z),z3p000(z);z)在U中单叶,且满足条件
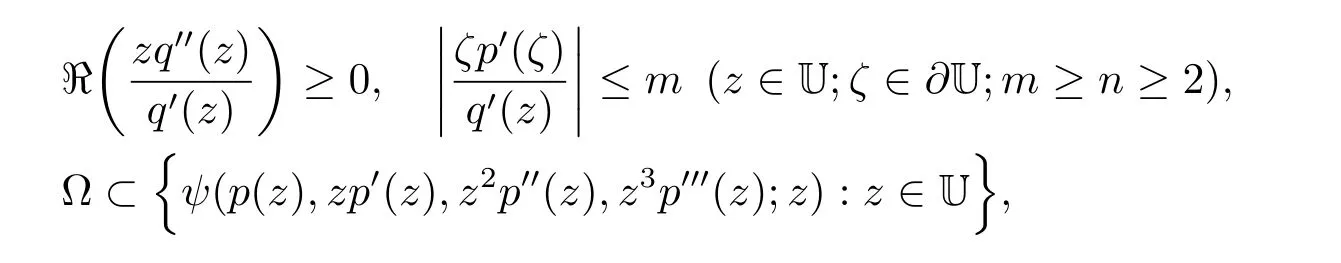
则q(z)≺p(z).
3 主要结果
本文研究关于算子Ws,bf(z)的微分从属与超从属的亚纯函数的性质,进而得到Sandwich型双从属结果.
定理3.1 设φ∈ΨΓ[Ω,q].如果f(z)∈Σ和q(z)∈Q1满足条件


所以在定义2.5中当φ∈ΦΓ[Ω,q]时,结果可被证明.也可等价的看作ψ在定义2.2的条件n=2时可证明结果.注意到
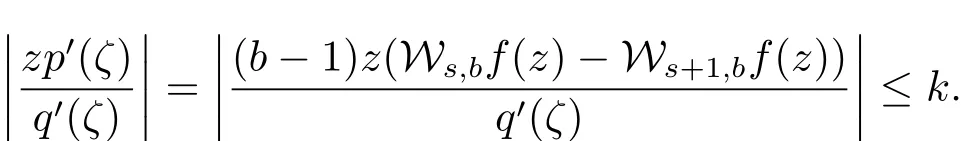
因此ψ∈Ψ2[Ω,q]且通过引理2.1,得到定理3.1.
如果Ω 6=C是一个单连通区域,且Ω=h(U)对U中的一些共形映射h(z)到Ω,则函数类ΦΓ[h(U),q]被看作ΦΓ[h,q].可以得到以下结果.
推论3.1 设φ∈ΦΓ[h,q].如果f(z)∈Σ和q(z)∈Q1满足条件
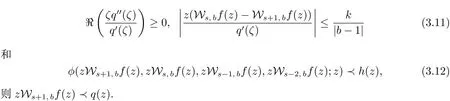
下面的推论是定理3.1的推广,其中q(z)在U的边界∂U是未知的.
推论3.2 设Ω⊂C,q(z)在U中单叶且q(0)=1.又设σ∈(0,1)对φ∈ΦΓ[Ω,qσ]成立,其中qσ(z)=q(σz).如果函数f(z)∈ Σ 满足

则zWs+1,bf(z)≺ q(z),其中z∈ U,ζ∈ UE(qσ).
证 通过定理3.1,可以得出zWs+1,bf(z)≺qσ(z).因此从qσ(z)≺q(z)可以得到结果的证明.
推论3.3 设Ω⊂C,q(z)在U中单叶且q(0)=1.又设σ∈(0,1)对φ∈ΦΓ[Ω,qσ]成立,其中qσ(z)=q(σz).如果函数f(z)∈ Σ 满足

则zWs+1,bf(z)≺ q(z),其中z∈ U,ζ∈ UE(qσ).

证 设函数p(z)和ψ分别被(2.1)式和(3.9)式定义.因为φ∈Φ0Γ[Ω,q],所以从 (3.10)式和(3.18)式推出

如果Ω 6=C是一个单连通区域,且Ω=h(U)对U中的一些共形映射h(z)到Ω,则函数类[h(U),q]被看作[h,q].可以得到以下结果.
推论3.4 设φ∈Φ0Γ[h,q]且h(z)在U中解析.如果函数f(z)∈Σ,zWs,bf(z)∈Q1和
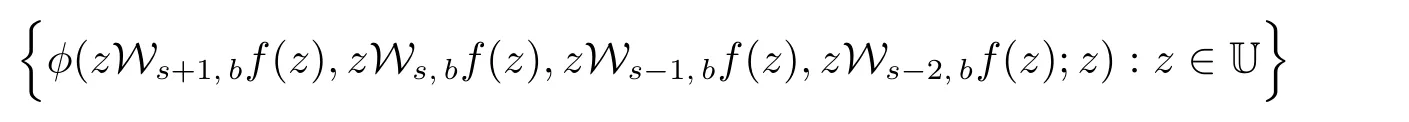
是单叶的,且

结合推论3.1和推论3.4,得到下面的Sandwich型双从属结果.
推论3.5 设h1(z)和q1(z)在U中解析,h2(z)在U中单叶,q2(z)∈Q1且q1(0)=q2(0)=1,φ ∈ ΦΓ[h,q]∩[h,q].如果函数f(z)∈ Σ,zWs+1,bf(z)∈Q1∩H 和

在U中单叶,且满足条件(3.11)式和(3.17)式,则可由
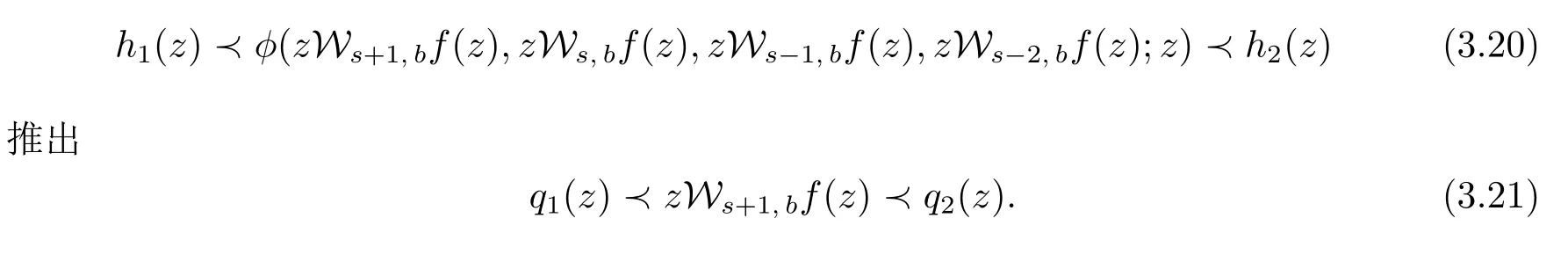
猜你喜欢
杂志排行
数学杂志的其它文章
- WEIGHTED MIXED INEQUALITIES ON PRODUCT SPACES WITH MUCKENHOUPT BASES
- OPTIMAL TIME-CONSISTENT INVESTMENT AND REINSURANCE STRATEGIES FOR MEAN-VARIANCE INSURER UNDER THE DEPENDENT RISK MODEL
- CONSTACYCLIC CODES OF LENGTH 2sOVER F2+uF2+vF2+uvF2
- HIGH-DIMENSIONAL VARIABLE SELECTION WITH THE GENERALIZED SELO PENALTY
- OPTIMAL DIVIDENDS WITH EXPONENTIAL AND LINEAR PENALTY PAYMENTS IN A DUAL MODEL
- CHARACTERIZATIONS OF SOBOLEV CLASSES OF BANACH SPACE-VALUED FUNCTIONS ON METRIC MEASURE SPACE
