胡献国,郭梦甜,吕家凤

(浙江师范大学 数学系, 浙江 金华 321004)

0 引 言

Poisson代数的概念起源于Poisson几何, 可简单看作交换代数与Lie代数的结合. 近年来，随着Poisson代数的广泛应用, 得到了多种Poisson代数的推广形式[1-4]. 特别地, DRINFEL’D[5]定义了Poisson Hopf代数，详细研究了这类代数在Poisson-Lie群上的应用. 此外, 吕家凤等[6]给出了Poisson Hopf代数及其泛包络代数的基本性质. 微分分次代数起源于代数拓扑与表示理论, 在交换代数与非交换代数领域有重要作用[7-8]. 作为其推广, LYU等[9]引入了微分分次Poisson代数, 研究了这类代数的张量积及相关性质和应用. 受此启发, 本文尝试将Poisson Hopf代数的概念推广到微分分次的情形, 定义了p次微分分次Poisson Hopf代数, 并推广了文献[9]的相关结果： 证明了任意2个p次微分分次Poisson Hopf代数的张量积仍为p次微分分次Poisson Hopf代数; 证明了p次微分分次Poisson Hopf代数构成的范畴dg-PHA是对称monoidal范畴.

本文的主要结果如下：

定理1(1) 设(A,uA,ηA,ΔA,εA,SA,{·,·}A,dA)和(B,uB,ηB,ΔB,εB,SB,{·,·}B,dB)是任意2个p次微分分次Poisson Hopf代数，则

(A⊗B,u,η,Δ,ε,S,{·,·},d)

也是p次微分分次Poisson Hopf代数.相关运算定义为：

S(a⊗b)∶=SA(a)⊗SB(b),

η(1k)∶=1A⊗1B,ε(a⊗b)∶=εA(a)εB(b),

u((a⊗b)⊗(a′⊗b′))∶=(-1)|a′||b|aa′⊗bb′,

Δ(a⊗b)∶=(-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2),

d(a⊗b)∶=dA(a)⊗b+(-1)|a|a⊗dB(b),

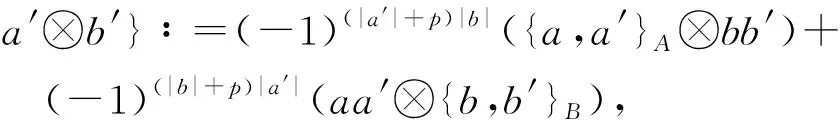
其中,uA(a⊗a′)∶=aa′,uB(b⊗b′)∶=bb′,

ΔA(a)∶=a(1)⊗a(2), ΔB(b)∶=b(1)⊗b(2), ||表示齐次元的次数,a,a′∈A,b,b′∈B为齐次元.

(2) 记dg-PHA为p次微分分次Poisson Hopf代数构成的范畴, 则dg-PHA是对称monoidal范畴, 其左单位元与右单位元均为基础域k.

(3) 设Aop与Bop分别为A与B的p次微分分次Poisson Hopf反代数. 则

(A⊗B)op=Aop⊗Bop.

1 p次微分分次Poisson Hopf代数

首先，回顾一些后面要用到的概念.

如无特别说明, 文中所有代数均含有单位元1,k表示特征为0的基域, 所涉及的对象都是域k上的向量空间, 所涉及的分次均为Z-分次. 对任给的分次向量空间V与W, 扭转映射是指

T：V⊗W→W⊗V∶T(v⊗w)=(-1)|v||w|w⊗v,

其中，v∈V,w∈W.

文中的分次代数A为Z-非负分次代数(A,u,η), 其中A=⊕n≥0An满足A0=k,u∶A⊗A→A与η∶k→A分别被称为A的乘法与单位. 方便起见, 记u(a⊗b)为ab, ∀a,b∈A. 而微分分次代数是指具有次数是1的微分d：A→A分次代数, 并且其是一个分次导子.

定义1设(A,·)是分次k-代数. 若存在k-齐次线性映射：

{·,·}∶A⊗A→A, |{·,·}|=p,

对于任意的齐次元a,b,c∈A, 满足

(i) (A,{·,·})是p次分次Lie代数, 即

(ia) {a,b}=-(-1)(|a|+p)(|b|+p){b,a},

(ib) {a,{b,c}}={{a,b},c}+

(-1)(|a|+p)(|b|+p){b,{a,c}}，

(ii) 分次交换性：a·b=(-1)|a||b|b·a,

(iii) 双导子性质： {a,b·c}={a,b}·c+

(-1)(|a|+p)|b|b·{a,c}，

则称(A,·,{·,·})为p次分次Poisson代数[10]. 若在此基础上, 存在1次k-线性映射d：A→A, 满足d2=0与

(iv)d({a,b})={d(a),b}+(-1)(|a|+p){a,d(b)},

(v)d(a·b)=d(a)·b+(-1)|a|a·d(b),

其中a,b∈A为齐次元, 则称A为p次微分分次Poisson代数, 可表示为(A,·,{·,·},d). 在不引起混淆的情况下, 可表示为(A,{·,·},d)或A.

文中的分次余代数(C,Δ,ε)为非负分次向量空间C, 具有次数为0的k-齐次线性映射

Δ∶C→C⊗C与ε∶C→k,

使得通常的图表可交换[11-12]. 注意到

k⊗C≅C≅C⊗k

是明显同构的, 因此，非负分次向量空间C是分次余代数当且仅当(C,Δ,ε)满足：

(Δ⊗I)Δ=(I⊗Δ)Δ,

(ε⊗I)Δ=I=(I⊗ε)Δ,

其中，I∶C→C恒等同态, Δ与ε分别称为C的余乘法与余单位. 在不引起混淆的情况下, 可将(C,Δ,ε)记为C.

对于任给的c∈C, 参照文献[12]中的记号, 记Δ(c)∶=∑(c)c(1)⊗c(2). 在使用过程中, 求和符号经常省略，因此, 对任给的齐次元c∈C, 余乘法与余单位可分别表示为

(Δ⊗I)Δ(c)=(I⊗Δ)Δ(c)=c(1)⊗c(2)⊗c(3)

与

c=ε(c(1))c(2)=c(1)ε(c(2)).

设(C,ΔC,εC)与(D,ΔD,εD)是2个分次余代数, 如果f满足条件：

(f⊗f)∘ΔC=ΔD∘f,εD∘f=εC,

则称次数为0的分次线性映射f∶C→D为分次余代数同态.

定义2设H是分次k-向量空间. 若存在1次k-线性映射d：H→H, 满足d2=0与

(i) (H,Δ,ε,d)是微分分次余代数, 即

(ia) (H,Δ,ε)是分次余代数,

(ib)d是次数为1的分次余导子，即有εd=0 与 Δd=(d⊗I+T(d⊗I)T)Δ，

(ii) (H,u,η,d)是微分分次代数,

(iii) Δ与ε是分次代数同态，

则称H为微分分次双代数. 若在此基础上, 存在次数为0的齐次线性映射S∶H→H, 满足

u(I⊗S)Δ=u(S⊗I)Δ=ηε，

则称(H,u,η,Δ,ε,S,d)为微分分次Hopf代数[13], 并称S为H的对极.

注记1在定义2的(ib)中, 若使用文献[12]中的记号, 对任给的齐次元x∈H, 则有

Δ(d(x))=d(x(1))⊗x(2)+(-1)|x(1)|x(1)⊗d(x(2)).

设(C,ΔC,εC)与(D,ΔD,εD)是2个分次双代数, 若f既是分次代数同态, 又是分次余代数同态，则称次数为0的分次线性映射f：C→D为分次双代数同态 . 更进一步, 若(C,SC)与(D,SD)都是分次Hopf代数，则易证f为分次Hopf代数同态, 即SD∘f=f∘SC( 参见文献[12] 引理4.0.4).

定义3设A是分次k-向量空间. 若存在k-齐次线性映射：

{·,·}∶A⊗A→A, |{·,·}|=p;

d∶A→A, |d|=1,

满足d2=0与

(i) (A,u,η,{·,·},d)是p次微分分次Poisson代数,

(ii) (A,u,η,Δ,ε,d)是微分分次双代数,

(iii) Δ({a,b}A)={Δ(a),Δ(b)}A⊗A, ∀a,b∈A，

其中{·,·}A⊗A定义为

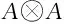
(-1)(|a′|+p)|b|(ab⊗{a′,b′}),

a,b,a′,b′∈A为齐次元，

则称(A,u,η,Δ,ε,{·,·},d)为p次微分分次Poisson双代数. 若在此基础上, 存在次数为0的k-齐次线性映射S∶A→A, 满足

u(I⊗S)Δ=u(S⊗I)Δ=ηε，

则称A为p次微分分次Poisson Hopf代数,表示为(A,u,η,Δ,ε,S,{·,·},d).

定义4设A与B是任意2个p次微分分次Poisson Hopf代数, 若对任给的齐次元a,b∈A, 有fdA=dBf,f({a,b}A)={f(a),f(b)}B，则称次数为0的分次双代数同态f∶A→B为微分分次Poisson Hopf代数同态. 进一步, 若微分分次Poisson Hopf代数同态f∶A→B是双射的, 则称作为微分分次Poisson Hopf代数的A与B是同构的, 记为A≅B.

记dg-PHA为p次微分分次Poisson Hopf代数构成的范畴, 其中的态射为微分分次Poisson Hopf代数同态.

下面给出具体的例子.

例1设(A,u,η,Δ,ε,S,{·,·},d)为任给的p次微分分次Poisson Hopf代数. 那么

(Aop,uop,η,Δop,ε,S,{·,·}op,d)

也为p次微分分次Poisson Hopf代数, 其中，

uop(a⊗b)=(-1)|a||b|b·a=a·b=u(a⊗b),

{a,b}op=(-1)(|a|+p)(|b|+p){b,a}=-{a,b},

Δop=TΔ,

a,b∈A为齐次元,T∶A⊗A→A⊗A为扭转映射, 即T(a⊗b)=(-1)|a||b|b⊗a.

d(x)=y,d(y)=0,

且{x,y}=-{y,x}=y2, {x,x}={y,y}=0. 定义分次Hopf代数的结构如下：

Δ(x)=x⊗1+1⊗x, Δ(y)=y⊗1+1⊗y,

ε(x)=0,ε(y)=0,S(x)=-x,S(y)=-y.

注意到在A中有y2=0. 易证A是1次微分分次Poisson Hopf代数.

2 定理1的证明

简单起见, 在不引起混淆的情况下, 下文中常省去下标. 所取的元素都是对应代数中的齐次元.

根据定义3, 定理1的证明可以分解成以下几个引理.

引理1由定理1中的定义, 有(A⊗B,Δ,ε)为分次余代数.

证明因为(A,Δ,ε)是分次余代数, 由分次余代数的定义, 有

a(11)⊗a(12)⊗a(2)=a(1)⊗a(21)⊗a(22),

ε(a(1))a(2)=a=a(1)ε(a(2)).

对分次余代数(B,Δ,ε), 有类似的等式成立. 从而

(Δ⊗I)Δ(a⊗b)=

(Δ⊗I)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)|a(2)|(|b(11)|+|b(12)|)+|a(12)||b(11)|a(11)⊗b(11)⊗

a(12)⊗b(12)⊗a(2)⊗b(2)=

(-1)|a(2)||b(1)|+|a(3)||b(1)|+|a(3)||b(2)|a(1)⊗b(1)⊗

a(2)⊗b(2)⊗a(3)⊗b(3),

(I⊗Δ)Δ(a⊗b)=

(I⊗Δ)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)(|a(21)|+|a(22)|)|b(1)|+|a(22)||b(21)|a(1)⊗b(1)⊗

a(21)⊗b(21)⊗a(22)⊗b(22)=

(-1)|a(2)||b(1)|+|a(3)||b(1)|+|a(3)||b(2)|a(1)⊗b(1)⊗

a(2)⊗b(2)⊗a(3)⊗b(3),

(I⊗ε)Δ(a⊗b)=

(I⊗ε)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)|a(2)||b(1)|(a(1)⊗b(1))·ε(a(2))ε(b(2))=

(-1)|a(2)||b(1)|a(1)ε(a(2))⊗b(1)ε(b(2))

与

(ε⊗I)Δ(a⊗b)=

(ε⊗I)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)|a(2)||b(1)|ε(a(1))ε(b(1))·(a(2)⊗b(2))=

(-1)|a(2)||b(1)|ε(a(1))a(2)⊗ε(b(1))b(2).

进而有

(Δ⊗IA⊗B)Δ=(IA⊗B⊗Δ)Δ.

注意到εA与εB均为次数为0的齐次线性映射, 且k为次数聚集在0处的分次向量空间, 所以对任意i>0, 有εA(Ai)=0与εB(Bi)=0, 其中A=⊕i≥0Ai，B=⊕i≥0Bi. 同理可得, Δ(An)⊆⊕i+j=nAi⊗Aj, 其中n≥0. 因此, 只有在a(2)∈A0时, 才有εA(a(2))≠0, 此时(-1)|a(2)||b(1)|=1. 故

(I⊗ε)Δ(a⊗b)=(-1)|a(2)||b(1)|a(1)ε(a(2))⊗

b(1)ε(b(2))=a(1)ε(a(2))⊗b(1)ε(b(2))=a⊗b.

类似地, 有 (ε⊗I)Δ(a⊗b)=a⊗b.

由此可得, (A⊗B,Δ,ε)为分次余代数.

引理2由定理1中的定义, 有εd=0, 且

Δd=(d⊗IA⊗B+T(d⊗IA⊗B)T)Δ.

证明注意到εAdA=0与εBdB=0. 因此

εd(a⊗b)=ε(d(a)⊗b+(-1)|a|a⊗d(b))=

εd(a)ε(b)+(-1)|a|ε(a)εd(b)=0.

下面证明Δ与微分的交换性. 根据Δ与d的结构, 可得

Δd(a⊗b)=Δ(d(a)⊗b+(-1)|a|a⊗d(b))=

(-1)|d(a)(2)||b(1)|d(a)(1)⊗b(1)⊗d(a)(2)⊗b(2)+

(-1)|a(1)|+|a(2)|+|a(2)||d(b)(1)|a(1)⊗d(b)(1)⊗a(2)⊗

d(b)(2)=(-1)|a(2)||b(1)|+|a(1)|+|b(1)|a(1)⊗b(1)⊗

d(a(2))⊗b(2)+(-1)|a(2)||b(1)|d(a(1))⊗b(1)⊗

a(2)⊗b(2)+(-1)|a(1)|+|a(2)||b(1)|a(1)⊗d(b(1))⊗

a(2)⊗b(2)+(-1)|a(1)|+|a(2)|+|b(1)|+|a(2)||b(1)|a(1)⊗b(1)⊗

a(2)⊗d(b(2))，

(d⊗I+T(d⊗I)T)Δ(a⊗b)=(d⊗I+T(d⊗

I)T)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)|a(2)||b(1)|d(a(1)⊗b(1))⊗a(2)⊗b(2)+

(-1)|a(2)||b(1)|+|a(1)⊗b(1)|a(1)⊗b(1)⊗d(a(2)⊗b(2))=

(-1)|a(2)||b(1)|[(d(a(1))⊗b(1)+(-1)|a(1)|a(1)⊗

d(b(1)))⊗a(2)⊗b(2)+(-1)|a(1)|+|b(1)|a(1)⊗

b(1)⊗(d(a(2))⊗b(2)+(-1)|a(2)|a(2)⊗d(b(2)))].

故

Δd=(d⊗IA⊗B+T(d⊗IA⊗B)T)Δ.

引理3由定理1中的定义, 有Δ与ε为分次代数同态.

证明先证Δ为分次代数同态. 注意到对任给的齐次元a,a′∈A, 有

Δ(aa′)=Δ(a)Δ(a′)=

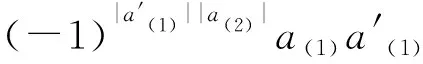
同理, 由ΔB为分次代数同态, 可推出

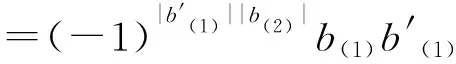
其中b,b′∈B为齐次元.

从而有

Δ((a⊗b)(a′⊗b′))=Δ((-1)|a′||b|aa′⊗bb′)=

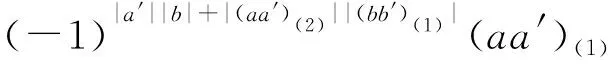
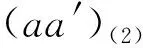
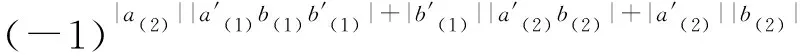
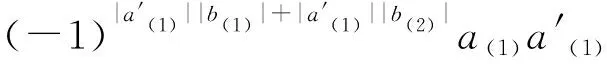
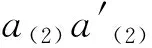
Δ(a⊗b)Δ(a′⊗b′)=(-1)|a(2)||b(1)|a(1)⊗b(1)⊗

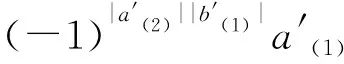
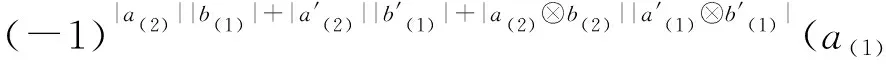
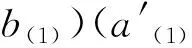
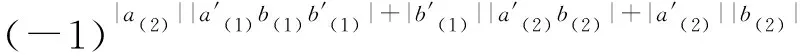
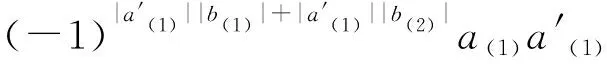
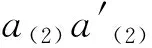
因此

Δ((a⊗b)(a′⊗b′))=Δ(a⊗b)Δ(a′⊗b′).

接下来证ε为分次代数同态.

ε((a⊗b)(a′⊗b′))=ε((-1)|a′||b|aa′⊗bb′)=

(-1)|a′||b|ε(aa′)ε(bb′)=

(-1)|a′||b|ε(a)ε(a′)ε(b)ε(b′)=

ε(a)ε(b)ε(a′)ε(b′)=ε(a⊗b)ε(a′⊗b′).

引理4由定理1中的定义, 有

Δ({a⊗b,a′⊗b′})={Δ(a⊗b),Δ(a′⊗b′)}.

证明注意到对任给的齐次元a,a′∈A, 有

Δ({a,a′})={Δ(a),Δ(a′)}=

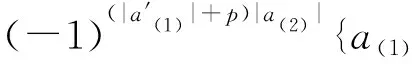
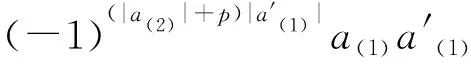
同理, 有

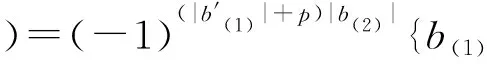
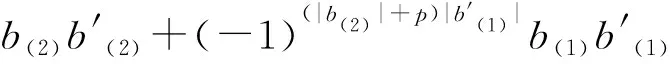
其中b,b′∈B为齐次元.

从而有

{Δ(a⊗b),Δ(a′⊗b′)}={(-1)|a(2)||b(1)|a(1)⊗

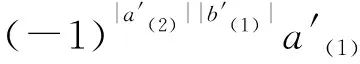
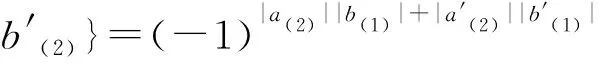
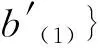
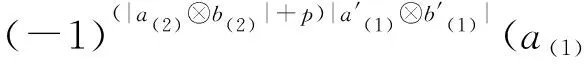
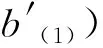
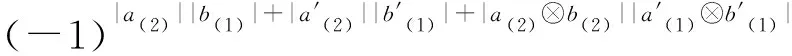
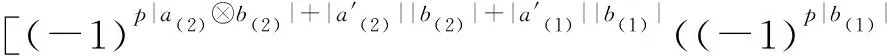
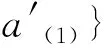
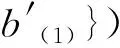
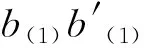
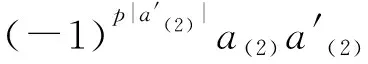
与

Δ({a⊗b,a′⊗b′})=Δ((-1)(|a′|+p)|b|{a,a′}⊗

bb′+(-1)(|b|+p)|a′|aa′⊗{b,b′})=

(-1)(|a′|+p)|b|Δ({a,a′}⊗bb′)+

(-1)(|b|+p)|a′|Δ(aa′⊗{b,b′})=

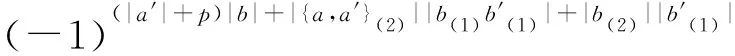
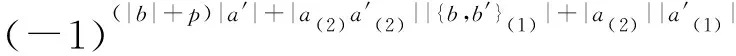
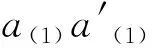
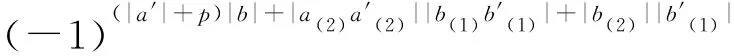
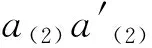
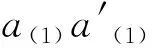
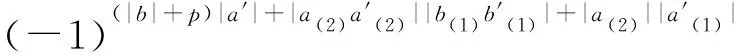
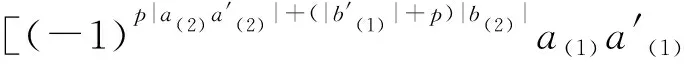
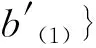
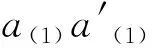
分别比较各项系数, 可得

Δ({a⊗b,a′⊗b′})={Δ(a⊗b),Δ(a′⊗b′)}.

引理5由定理1中的定义, 有S为A⊗B的对极, 即

u(I⊗S)Δ=u(S⊗I)Δ=ηε.

证明注意到

u(I⊗S)Δ(a⊗b)=

u(I⊗S)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)|a(2)||b(1)|(a(1)⊗b(1))S(a(2)⊗b(2))=

(-1)|a(2)||b(1)|(a(1)⊗b(1))(S(a(2))⊗S(b(2)))=

a(1)S(a(2))⊗b(1)S(b(2))=ε(a)ε(b)1A⊗B,

从而

ηε(a⊗b)=η(ε(a)ε(b))=ε(a)ε(b)1A⊗B=

u(I⊗S)(a⊗b).

类似地, 有

u(S⊗I)Δ=ηε.

定理1的证明(1) 由文献[9]可知, (A⊗B,u,η,d,{·,·})是p次微分分次Poisson代数. 再由引理1～引理5可得, (A⊗B,u,η,Δ,ε,S, {·,·},d)是p次微分分次 Poisson Hopf代数. 故(1)成立.

(2) 定义映射

φ：A⊗B→B⊗A，

φ(a⊗b)=(-1)|a||b|b⊗a,

其中，a∈A,b∈B为齐次元. 要证dg-PHA为对称monoidal范畴, 只须证φ是同构映射. 由于φ∘φ=1, 故只需证φ是微分分次Poisson Hopf代数同态. 注意到εA与εB都是次数为0的齐次线性映射, 所以有

ΔB⊗Aφ(a⊗b)=ΔB⊗A((-1)|a||b|b⊗a)=

(-1)|a||b|+|a(1)||b(2)|b(1)⊗a(1)⊗b(2)⊗a(2),

(φ⊗φ)ΔA⊗B(a⊗b)=

(φ⊗φ)((-1)|a(2)||b(1)|a(1)⊗b(1)⊗a(2)⊗b(2))=

(-1)|a||b(1)|+|a(2)||b(2)|b(1)⊗a(1)⊗b(2)⊗a(2)

与

εB⊗Aφ(a⊗b)=εB⊗A((-1)|a||b|b⊗a)=

(-1)|a||b|ε(b)ε(a)=ε(a)ε(b)=εA⊗B(a⊗b).

因此,φ是分次余代数同态. 注意到φ是微分分次Poisson代数同态,k是p次微分分次Poisson Hopf代数, 故结论成立.

(3) 由例1可知,Aop,Bop与(A⊗B)op都是p次微分分次Poisson Hopf代数. 注意到(A⊗B)op与Aop⊗Bop的代数结构均由(uop,η,Δop,ε,S,{·,·}op,d)所决定, 其中，

η(1k)： =1A⊗1B,
ε(a⊗b)： =εA(a)εB(b),
S(a⊗b)： =SA(a)⊗SB(b),
d(a⊗b)： =dA(a)⊗b+(-1)|a|a⊗dB(b),
uop((a⊗b)⊗(a′⊗b′))： =(-1)|a′||b|aa′⊗bb′,

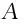
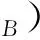
Δop(a⊗b)： =(-1)|a(1)||a(2)|+|a(1)||b(2)|+|b(1)||b(2)|×

a(2)⊗b(2)⊗a(1)⊗b(1),

a,a′∈A,b,b′∈B为齐次元. 故

(A⊗B)op=Aop⊗Bop.

证毕！