孔新海，马 新

（1.广安职业技术学院 智能制造与能源工程学院，四川 广安 638000；2.西南科技大学 理学院，四川 绵阳 621010）

0 引言

灰色系统理论自被提出以来，经过几十年的快速发展，已被广泛地应用于经济社会管理、工业企业生产等各个领域。它能够处理小样本贫信息问题，是处理这类问题方法体系，特别GM（1,1）模型是灰色系统理论中非常简洁且应用广泛的一类预测模型[1]。在应用过程中，为了提高模型精度，很多学者提出了优选初始值、优化灰导数或背景值等一系列的改进方法[2,3]；而针对建模序列的特点，提出了适合单调递增序列、单调递减序列或非等间距序列的GM（1,1）建模方法及其优化措施[4-9]。对于具有凹凸性的序列，文献[10]提出了用轴对称手段来改变原始序列凹凸性进行GM（1,1）建模的一种方法。本文针对原始序列是凸的情况，首先分析了GM（1,1）模型预测序列的特点，其次提出了改变序列凹凸性的一种新方法，即以原始序列首尾两点连线为对称轴，把凸序列转化为对称序列（凹序列），再基于对称序列建立非等间距GM（1,1）模型，从而对原序列进行预测。

1 凹（凸）序列的定义

定义1：设x（0）={x（0）（1），x（0）（2），…，x（0）（n）}为任意一组正序列，对任意k（2≤k≤n-1），若满足 Δ（0）（k）≤ Δ（0）（k-1），则称x（0）为凸序列；若满足 Δ（0）（k）≥ Δ（0）（k-1），则称x（0）为凹序 列 ，其中 Δ（0）（k）=x（0）（k）-x（0）（k-1）。 特别地 ，当Δ（0）（k）＜ Δ（0）（k-1）时 ，称x（0）为严格凸序列 ；当Δ（0）（k）＞ Δ（0）（k-1），称x（0）为严格凹序列。

定理 1：若序列x（0）={x（0）（1），x（0）（2），…，x（0）（n）} 是凸序列，则满足不等式：

2x（0）（k）≥x（0）（k+1）+x（0）（k-1）

若x（0）为凹序列，则满足不等式：

2x（0）（k）≤x（0）（k+1）+x（0）（k-1）

证 明 ：若x（0）是凸序列，则由定义 1 可知 Δ（0）（k）≤Δ（0）（k-1），即：

x（0）（k+1）-x（0）（k）≤x（0）（k）-x（0）（k-1）

从而 2x（0）（k）≥x（0）（k+1）+x（0）（k-1）。同理，可证x（0）为凹序列时，有 2x（0）（k）≤x（0）（k+1）+x（0）（k-1）。

2 原始GM（1,1）模型及其特性

定义 2[1]：设x（0）={x（0）（1），x（0）（2），…，x（0）（n）} 为一非负的原始序列 ，其一次累加序列为x（1）={x（1）（1），x（1）（2），…，x（1）（n）} ，均值序列为Z（1）={z（1）（2），z（1）（3），…，z（1）（n）} ，其中Z（1）（k）=0.5（x（1）（k）+x（1）（k-1））,则称下列离散等式：

式（1）为灰色GM（1,1）模型的均值形式，称微分方程。

式（2）为灰色GM（1,1）模型均值形式的白化微分方程。对式（1）由最小二乘法得参数a，b估计值。

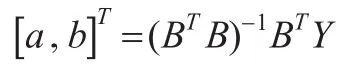
式中：

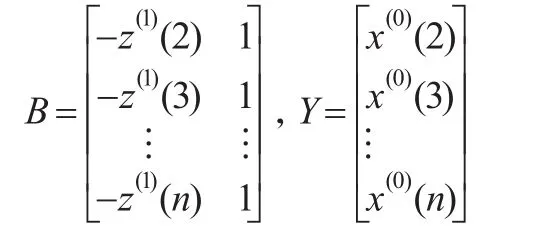
把参数a，b估计值代入式（2）,求得白化方程的解为：

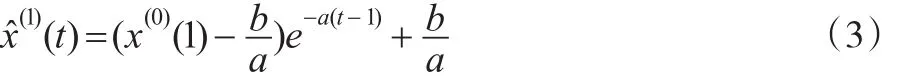
然后离散化,可得时间响应序列：

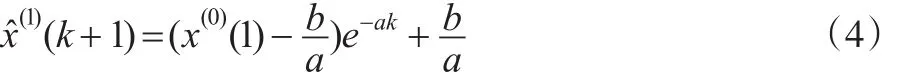
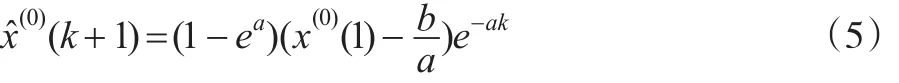
一般来说，GM（1,1）建模序列都是正数序列，如果是负数序列或正负混合序列，则可以通过平移变换转化为正数序列。因此，在应用GM（1,1）模型进行建模时，其拟合或预测序列也应该是正数序列。下面将论证GM（1,1）模型预测序列的一个显著特征。

定理2：GM（1,1）模型的拟合预测序列是凹的。

证明：对一切k=1，2，…，不妨假设式（5）都是正数，则有：

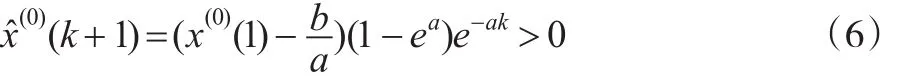
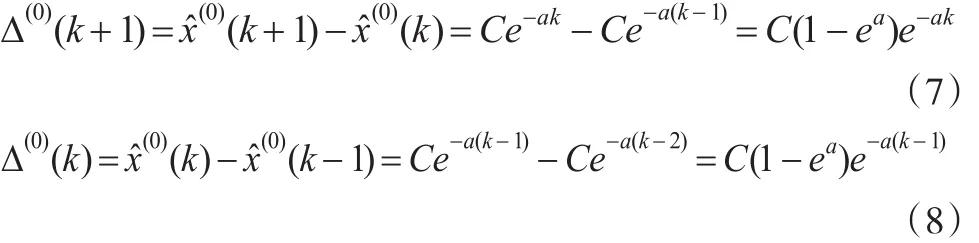
将式（7）与式（8）相比，有：

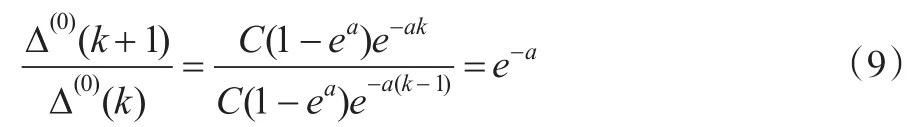
（1）当a＞0时，显然有e-a＜1，即:

由于 （1-ea）＜ 0 ，于是 Δ（0）（k）=C（1-ea）e-a（k-1）＜ 0 ，代入式（10）则有：

（2）当a＜0时，有e-a＞1，即:

由于 （1-ea）＞ 0 ，于是 Δ（0）（k）=C（1-ea）e-a（k-1）＞ 0 ，代入式（12）则有：

因此，无论原始序列具有什么特征，根据定义1可知GM（1,1）模型的模拟预测序列是凹的。

定理2实际上说明了GM（1,1）模型的拟合预测值是一个凹序列，当原始序列是凸序列时，用式（5）计算得到的GM（1,1）模型拟合序列与原始凸序列的几何形状完全相反。因此对原始凸序列直接进行GM（1,1）建模将会产生很大的误差，预测结果将与原始序列发展态势不一致。

3 原始凸序列的对称变换

根据前面对GM（1,1）模型特性分析可知，对原始凸序列进行GM（1,1）建模，会导致很大的模型误差。如果把凸序列转换成凹序列就可以避免这种模型误差。这里选取以第1个点和第n个点的连线作为对称轴（如图2所示），进行凹凸性对称转换。

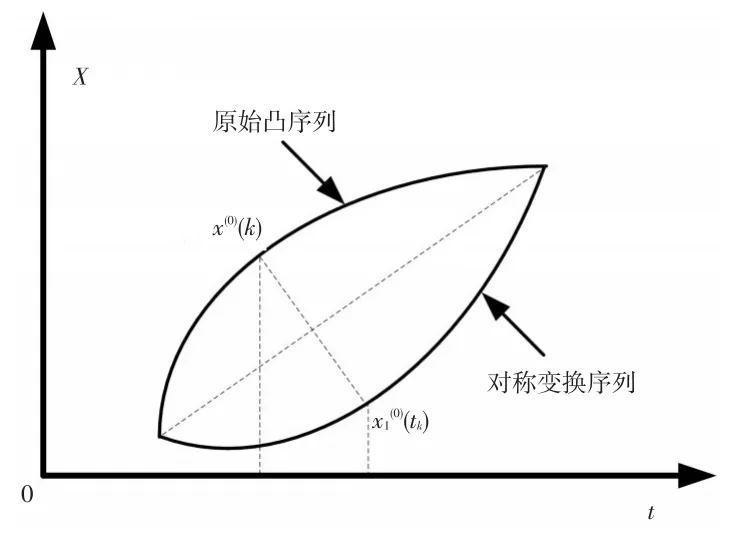
图1 原始凸序列的对称变换

定理 3:若X（0）={x（0）（1），x（0）（2），…，x（0）（n）} 为一正的凸序列，其初值化序列为，对进行对称变换，则得到凹序列，其中:

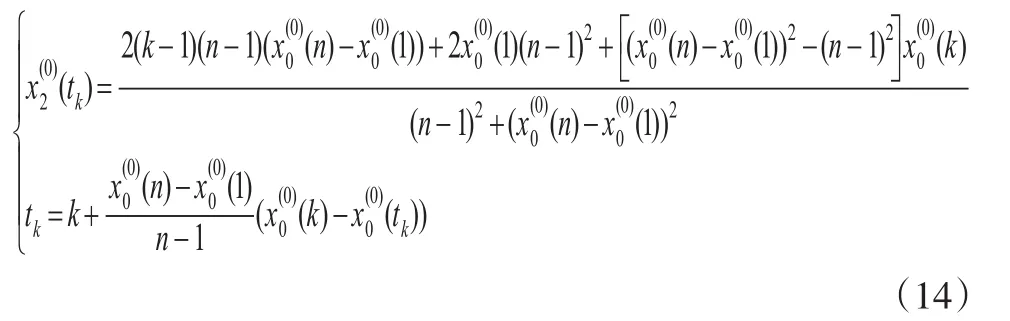
证明：由两点法，可得到对称轴的直线方程为:

对于任意一点 （k，（k）），其对称点为 （tk，（tk）），则两点中心满足式（15），即:

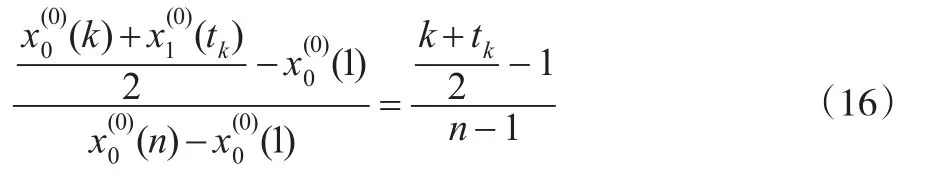
根据两条垂线斜率乘积为-1，有:

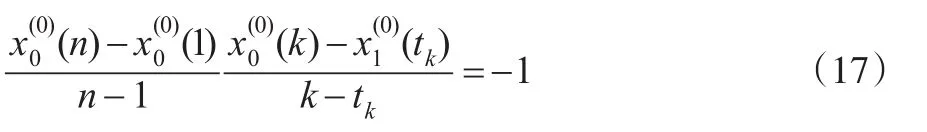
联立式（16）和式（17），即可解得式（14）。显然当k=1时，有当k=n时，有

4 基于凸序列对称变换非等间距GM（1,1）模型

对于原始凸序列经对称变换之后，由于Δtk（Δtk=tk-tk-1）不为常数，所以对称变换序列为非等间距序列。这就需要建立非等间距 GM（1,1）模型）+）=b，其与等间距GM（1,1）模型的不同之处在于：

（1）间距序列

Δt={Δt1，Δt2，…，Δtn}，Δt1=1，

Δtk=tk-tk-1，k=2，3，…，n

（2）一次累加序列

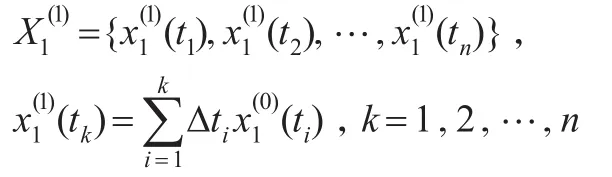
（3）紧邻均值序列

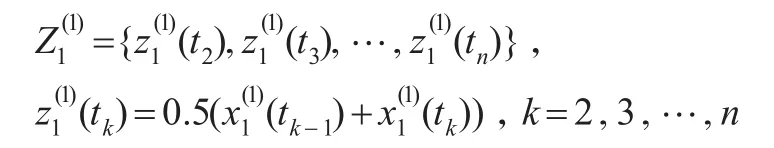
（4）响应函数序列

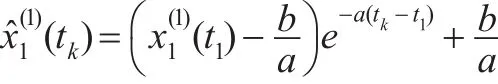
（5）还原值序列

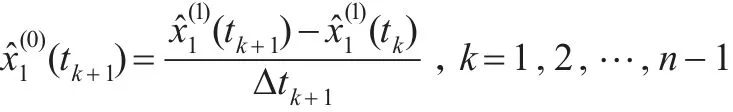
因此，对于凸序列，应用GM（1,1）模型进行预测，首先要对原始序列进行初值化，然后对初值化序列进行对称变换，基于对称序列建立GM（1,1）模型，进而由GM（1,1）模型预测对称序列，最后再逆变换可得原始序列的预测值。具体步骤如下：

第一步：对于一正凸数据序列x（0）={x（0）（1），x（0）（2），…，，先对原始序列初值化变换，得初值化序列；

第三步：基于对称序列建立非等间距GM（1,1）模型，得拟合序列

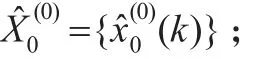
第五步：计算还原值序列

5 实例分析

例1[11]:我国2009—2015年人均天然气生活消费量为X（0）={13.3，17.0，19.7，21.3，23.8，25.1，26.2} ，单位：立方米。这是个单调递增具有上凸特征的序列，这里用本文方法对原始数据进行对称变换再建立GM（1,1）模型，其模拟结果见表1所示。

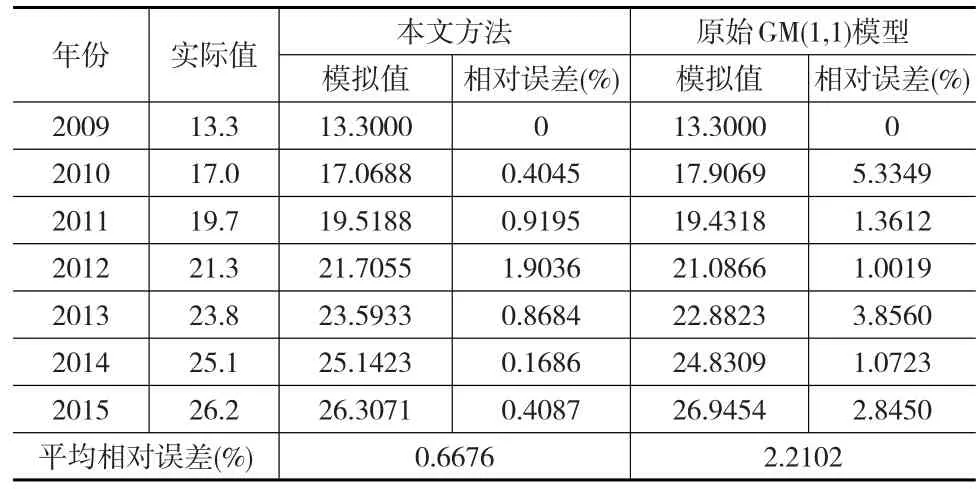
表1 基于GM（1,1）模型2009—2015年我国人均天然气生活消费量模拟结果

从表1可以看出，本文方法拟合平均相对误差明显小于直接GM（1,1）建模的平均相对误差。因此，对于单调递增的凸数据序列，需要把凸数据序列转化为凹数据序列进行GM（1,1）建模，其建模精度更高。

例2：萨莫特洛尔油田是俄罗斯的第一大油田，1969年投产，1980年的产量达到峰值，在1980—1988年递减阶段的年产量分别为：X（0）={15.48，15.03，14.38，14，13.06，12.09，10.98，9.88，8.27}，其单位：107t/年。这显然是个单调递减的凸数据序列，如果也用本文中给出方法进行数据对称变换再建立GM（1,1）模型，模拟结果见表2所示。

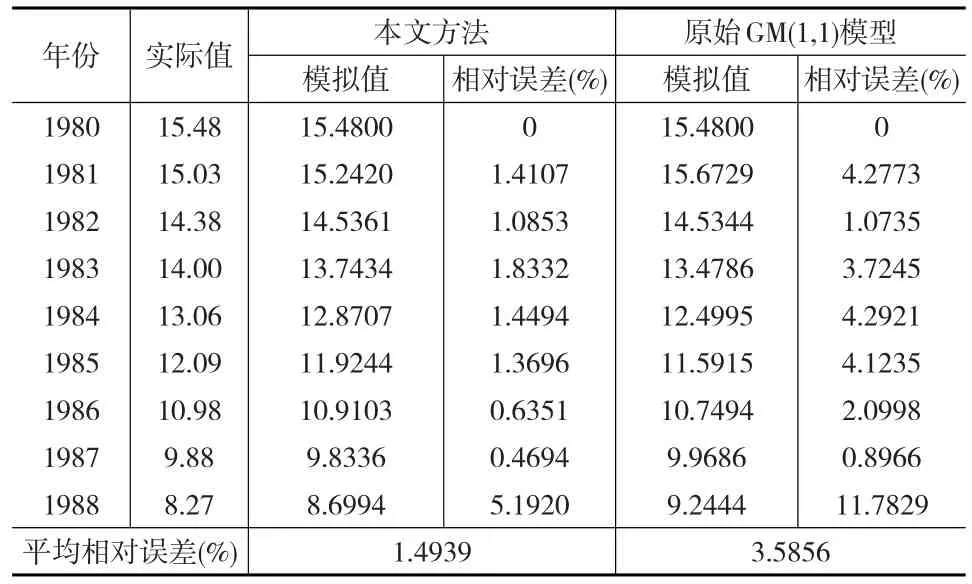
表2 基于GM（1,1）模型萨莫特洛尔油田递减阶段的年产量模拟结果

表2比较结果也显示：本文方法拟合误差比直接GM（1,1）建模误差要小很多。因此，对于单调递减的凸数据序列，同样需要对凸数据序列进行凹凸性转换，才能取得更好的GM（1,1）建模效果。

6 结束语

根据本文证明可知，GM（1,1）模型的模拟预测序列具有凹向性，因此GM（1,1）模型适合凹数据序列建模。对于凸数据序列，要使得预测结果符合原始序列的发展趋势，需要对原始数据进行对称变换，否则预测结果失真。经过进一步研究发现，对于凸数据序列采用GM（1,1）模型预测时，仅对GM（1,1）模型参数进行优化，GM（1,1）模型拟合精度并不能有效提高，其预测结果更偏离原始序列发展趋势。要想从根本上解决模型误差，可以借助对称变换，把原始序列是凸的转换成凹的，然后再进行GM（1,1）建模。