特征匹配驱动的IVIFSs相似性测度模型研究
2018-11-09江文奇祁晨晨
江文奇, 祁晨晨
(1. 南京理工大学经济管理学院, 江苏 南京 210094; 2. 江苏产业集群决策咨询研究基地, 江苏 南京 210094)
0 引 言
直觉模糊型多准则决策问题是近年来多准则决策研究领域的热点问题之一。传统的直觉模糊集(intuitionistic fuzzy sets, IFSs)采用隶属度、非隶属度和犹豫度表征评估值,但是忽视了决策信息的模糊性和决策者认知的局限性[1]。区间直觉模糊集(interval-valued intuitionistic fuzzy sets,IVIFSs),使用区间值来表示隶属度、非隶属度和犹豫度,增强了表达信息的不确定性能力,可以有效处理数据的不确定性和模糊性[2]。
IFSs相似性测度是直觉模糊型多准则决策的重要环节,在模式识别等领域得到广泛应用[3]。文献[4-5]最先提出了IFSs相似性测度距离模型,文献[6]分析了这两个模型的缺点并进行了改进。2002年,李登峰等提出了IFSs的相似性测度模型,被国际学者命名为登峰-春田相似性测度,为相似度设计奠定了研究基础[7-8]。文献[9]基于直接算子重新定义了相似性测度。文献[10]则根据反直觉的案例重新定义了相似性测度模型。文献[11]运用几何距离模型重新定义了连续距离和相似性测度。文献[12]拓展了基数测度,设计了基于t范数的相似性测度。文献[13]则基于Hausdorff距离计算IFSs间的距离进而提出新的相似性测度模型。文献[14]指出一些相似性测度并不有效,提出了几种新的测度模型。文献[15]运用欧式距离进行相似性度量;文献[16]将IFSs转化为直角三角形,基于重心提出相似性度量模型。
IVIFSs相似性测度分成两类,第一类设计借鉴IFSs相似性测度思想。文献[17]分别利用区间数中点值和Hausdorff距离定义相似性测度。文献[18]结合IFSs的Hamming距离和补集提出了IVIFSs相似性测度。文献[19]设计包含犹豫度的IVIFSs欧氏距离公式。文献[20]分别将文献[11]中IFSs相似度拓展至IVIFSs相似性测度中。
另一种类型是设计全新的相似性测度模型。文献[21-23]构建了IVIFSs的熵和相似性测度的关联性,进而设计了基于熵的相似性测度。文献[24]采用shapely函数定义了几个赋权的shapely相似性测度模型。文献[25]对IVIFSs进行约简,进而提出了Dice相似性测度。文献[26]考虑了犹豫度因素并运用相关系数表示相似度。文献[27]考虑了犹豫度对隶属度和非隶属度的影响,结合TOPSIS构建相似性模型。文献[28]考虑隶属度、非隶属度和区间中点的影响并定义了新的相似度。文献[29]分别考虑隶属度与非隶属度的距离,提出了新的相似性模型。
总体上看,IFSs的相似性测度主要以距离测度为主,采用左右端点分别比较的方式确定任意两个IFSs的隶属关系[30]。在含有IVIFSs的决策环境下,难以采用IFSs左右端点进行直接比较,因此提高了相似性测度特征匹配的难度。同时,IVIFSs相似性测度大部分考虑区间端点和中点值,容易造成信息损失,导致相似度测度模型可能不满足相似度性质,存在着反直觉现象,且部分IVIFSs相似性区分度不高,难以展现决策方案的差异性。于是,基于IVIFSs的特点,本文首先提出其相似性解释框架,分析现有IVIFSs相似性测度与解释框架匹配性难度,通过转换IVIFSs进而提出了一种新的IVIFSs相似性测度模型,并说明其科学性和应用价值。
1 IVIFSs相似性测度性质
定义1[1]设X是一给定论域,IFSA={〈x,μA(x),vA(x)〉|x∈X}。其中μA(x)和vA(x)分别为X中元素x属于A的隶属度和非隶属度。μA:X→[0,1],vA:X→[0,1],且满足条件0≤μA(x)+vA(x)≤1,x∈X。称πA(x)=1-μA(x)-vA(x)为X中x属于A的犹豫度。

定义3[7]如果映射S:IVIFS(X)×IVIFS(X) →[0,1],称S(A,B)为IFSA∈IVIFS(X)和B∈IVIFS(X)间的相似度,且满足5个特征条件:
① 0≤S(A,B)≤1;
②S(A,B)=1当且仅当A=B;
③S(A,B)=S(B,A);
④S(A,B)=0当且仅当A=〈[0,0],[1,1]〉,B=〈[1,1],[0,0]〉或A=〈[1,1],[0,0]〉,B=〈[0,0],[1,1]〉;
⑤ 如果A⊆B⊆C,则S(A,C)≤S(A,B),S(A,C)≤S(B,C)。
⑥SA≤SB≤SC。
⑦ 如果SA=SB=SC,则HA≤HB≤HC。
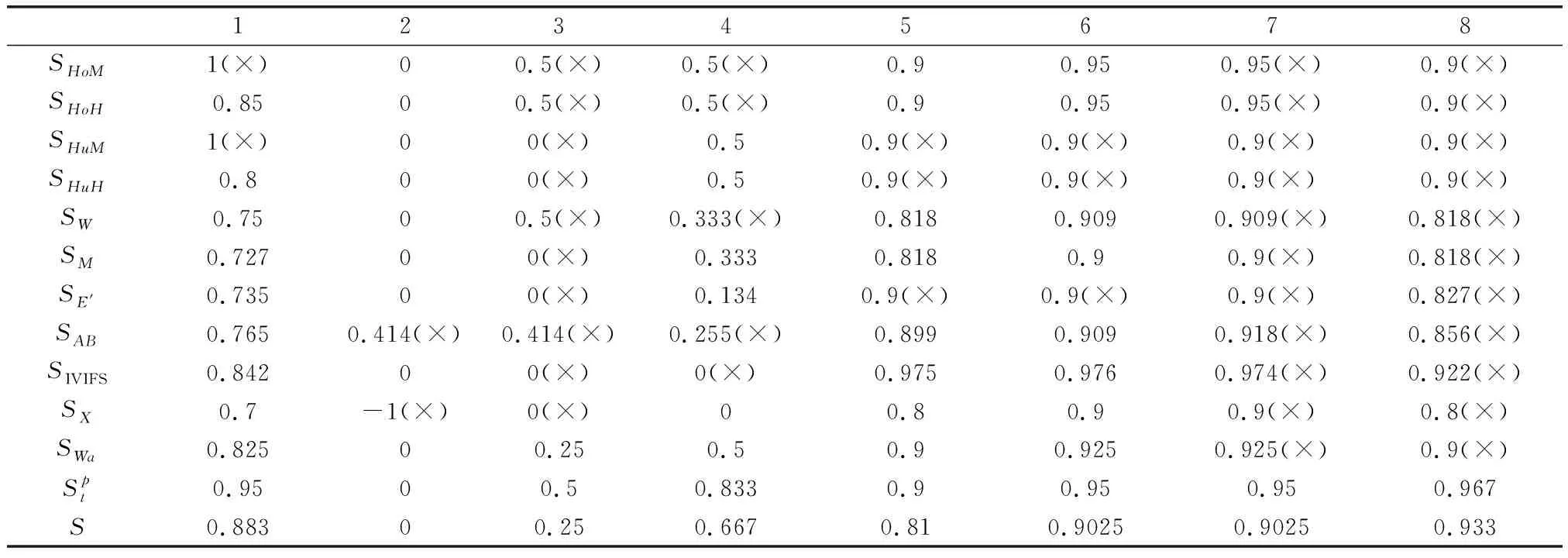
假设A=〈[0.3,0.5],[0.1,0.3]〉,B=〈[0.4,0.6],[0.2,0.4]〉,C=〈[0.4,0.6],[0.1,0.3]〉,采用区间数中点表示隶属度和非隶属度,A,B,C支持比率分别为0.667、0.625、0.714,故A和B相似度高于A和C,不满足条件⑤中A⊆B⊆C,采用条件⑥有SA=0.1,SB=0.2,SC=0.3,即S(A,C) (1) 基于Hamming距离的相似度为 (1) (2) 基于欧氏距离的相似度为 (2) (3) 基于Hausdorff距离与Hamming距离的相似度为 (3) (4) 基于Hausdorff与欧氏距离的相似度为 (4) (5) 分别利用区间数中点值和Hausdorff测度等相似性测度方法[17],得到 (5) (6) (7) (8) (6) 基于熵测度的相似度[22]为 (9) (7) Meng[24]改进了Wei的相似度,提出SM为 (10) (8) 在欧式距离中考虑犹豫度,有相似度[19]为 (11) (9) 结合TOPSIS的思想构建的相似度模型为 (12) 式中 (10) 用相关系数表示相似度,即 (13) 式中 CIVIFS(A,B)= EIVIFS(A)= EIVIFS(B)= (11)相似度为 (14) (12) 结合欧氏距离和Hausdorff距离的相似度为 (15) (13) Dügenci[20]拓展了文献[16]的相似度为 (16) (1)SH,SE,SHH,SHE只考虑了4个参数绝对值或平方,若他们相等则相似度相同,因此均不满足条件⑥。如当A=〈[0.25,0.35],[0.25,0.35]〉,B=〈[0.35,0.45],[0.35,0.45]〉,C=〈[0.25,0.35],[0.35,0.45]〉,D=〈[0.35,0.45],[0.25,0.35]〉时SH(A,B)=SH(C,D)=0.9,SE(A,B)=SE(C,D)=0.9;SHH(A,B)=SHH(C,D)=0.975,SHE(A,B)=SHE(C,D)=0.95,然而根据记分函数有C (2)SHH和SHE不满足条件④。当A=〈[1,1],[0,0]〉,B=〈[0,0],[1,1]〉时,SHH(A,B)=0.75,SHE(A,B)=0.5, 而A和B表示全部支持和全部反对,即S(A,B)=0,故SHH和SHE不合理。 (3)SHoM和SHuM违反了条件②、条件④和条件⑤。使用区间中点替代整个区间,会丢失原区间信息。如当A=〈[0.2,0.6],[0.2,0.4]〉,B=〈[0.4,0.4],[0.3,0.3]〉时,SHoM(A,B)=SHuM(A,B)=1,而A≠B;当A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉时,SHuM(A,B)=SHuH(A,B)=0,两者相似度为0并不合理;当A=〈[0.2,0.3],[0.4,0.6]〉,B=〈[0.3,0.4],[0.4,0.6]〉,C=〈[0.3,0.4],[0.3,0.5]〉,根据条件⑤有A⊆B⊆C,然而SHuM(A,B)=SHuM(A,C)=SHuH(A,B)=SHuH(A,C)=0.9。 (4)SHoM,SHoH,SHuM,SHuH违反条件⑥。如A=〈[0.35,0.45],[0.15,0.25]〉,B=〈[0.45,0.55],[0.25,0.35]〉,C=〈[0.45,0.55],[0.15,0.25]〉,由记分函数可得A (5)SW违反条件⑥。熵到相似度转换过程中使用的函数在某些情况下非区间直觉模糊数,反例同(4)。 (6)SM不满足条件④和条件⑥。改进后的相似度可以保证转换中的函数为IVIFSs,但当A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉时,SM(A,B)=0;其次不满足性质条件⑥,反例同(4)。 (7)SE′违反了条件④:当A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉时,SE′(A,B)=0;此外不满足性质条件⑤和条件⑥,反例同(3)与(4)。 (8)SAB违反了条件④:当A=〈[0,0],[1,1]〉,B=〈[1,1],[0,0]〉时,SAB(A,B)=0.414≠0;也同样违反了条件⑥,反例同(4)。 (9)SIVIFS违反条件④。考虑犹豫度,克服距离测度造成的信息混淆。但当A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉时,SIVIFS(A,B)=0;违反了条件⑥,反例同(4)。 (10)SX违反条件①和条件④:A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉时,SX(A,B)=-1;违反条件⑥,反例同(4)。 (11)SWa满足前5条性质,但违背条件⑥,反例同(4)。 如用“√”表示满足该性质,“×”表示不满足该性质,则上述分析结果可以总结如表1所示。 表1 现有文献满足约束条件情况 现有的IVIFSs相似性测度没有充分考虑式(5)中IVIFSs的隶属关系的局限性,故未能完全满足相似度性质。尽管从记分函数角度出发来刻画式(5),但仍然无法满足其特征要求,有必要重新设计一个新的相似度函数。借鉴文献[16]将IFS转换为三角模糊数而获取相似度的研究思路,本文考虑了IVIFSs端点不一致情形,将其转化为三角模糊数而设计相似度测度,具体设计如下。 令 则转化后的区间三角模糊数为 定义4A与B的相似度为 S(A,B)=[1-d(A,B)]×(1-|xA-xB|) (17) 式中 d(A,B)= (18) 重心分别为 /4 于是,证明定义4满足上述7个性质。 (3)S(A,B)=S(B,A)显然成立。 由以上可得S(A,C)≤S(A,B)。同理可得S(A,C)≤S(B,C)。 (6) 由SA≤SB≤SC,得 ≤0 6S(A,B)= {1-(SB-SA)/2}= {6-[2(HB-HA)+SB-SA]}×{1-(SB-SA)/2}= 6-4(SB-SA)- 2(HB-HA)+(HB-HA)(SB-SA)+(SB-SA)2/2 则 6(S(A,B)-S(A,C))= (SC-SB)[8-(SB+SC-2SA)]/2+[HB(SB-SA)+ HA(SC-SB)-HC(SC-SA)+2(HC-HB)] 其中 HB(SB-SA)+HA(SC-SB)- HC(SC-SA)+2(HC-HB)= (HB-HC)(SB-SA-2)+ HC(SB-SC)+HA(SC-SB)≥ (HA-HC)(SB-SA-2)+ (SC-SB)(HA-HC)= (HA-HC)(SC-SA-2) 得 12(S(A,B)-S(A,C))≥ (SC-SB)[8-(SB+SC-2SA)]+ 2(HA-HC)(SC-SA-2) 因为-4≤SB+SC-2SA≤4,得8-(SB+SC-2SA)≥0,即有:(SC-SB)[8-(SB+SC-2SA)]≥0。又HA-HC≤0,0≤SC-SA≤2,所以:(HA-HC)(SC-SA-2)≥0。因此有S(A,B)-S(A,C)≥0,即S(A,C)≤S(A,B)。 同理,S(A,C)≤S(B,C)。如果SA≤SB≤SC,如果为其他两种情形,也可以证明S(A,C)≤S(A,B),S(A,C)≤S(B,C)。 证毕 6S(A,B)= 6[1-(SA-SB)/2]2 则 S(A,B)-S(B,C)= [1-(SA-SB)/2]2-[1-(SB-SC)/2]2= [(SA-SB)2-(SB-SC)2]/4-(SA-2SB+SC)= (SA-2SB+SC)[(SA-SC)/4-1] 针对文献[31]的相似性测度式(16),当t=2,p=1时, (A,B)=12- 12-6(SA-SB) D1=|S(A,B)-S(B,C)|= |(SA-2SB+SC)|×(1-(SA-SC)/4) 因为-1≤SA≤1,-1≤SC≤1,有-2≤SA-SC≤2,0.5≤1-(SA-SC)/4≤1.5,因此D1≥D2,相比文献[31],本文的相似性测度具有较强的区分度和辨别能力。 接着本文拟从实证角度进行分析。将本文的方法与16种相似度测度进行比较,具体见表2。其中p=1,t=2,数字后有(×)表示不满足。 表2 区间直觉模糊数之间的各种相似度量方法比较 续表2 IVIFSs中的相互包含关系在现实中出现概率较低,导致其相似性测度模型很难与这种包含关系完全匹配。为了有效分析IVIFSs的隶属关系对相似性测度设计的影响,本文采用记分函数和精确函数来加以刻画,提出了新的IVIFSs的相似性测度性质解释框架,接着分析对比了现有相似性测度的缺陷,以本文构建的性质框架为切入点,将IVIFSs转换为区间三角模糊数,结合三角模糊数的距离和重心定义一个新的相似性测度函数,并通过理论证明验证本文提出的相似性测度不仅可以满足现有的和改进的相似性测度性质,而且比现有的相似性测度有更高的区分度。2 现有IVIFSs相似性测度分析
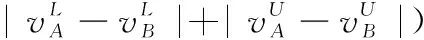
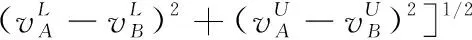
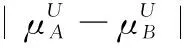

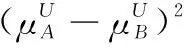
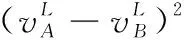

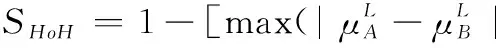

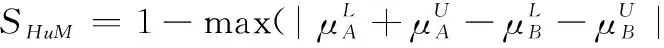

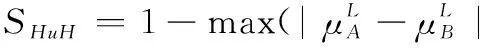

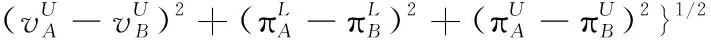
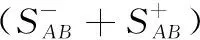
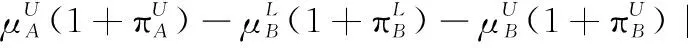
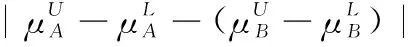
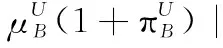

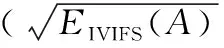
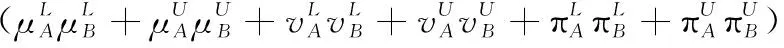

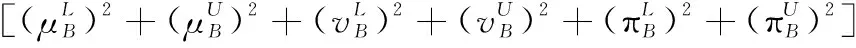
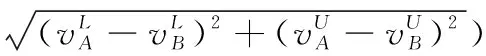
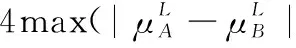

3 现有IVIFSs相似性测度性质分析


4 新的IVIFSs相似性测度设计
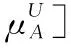
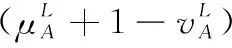
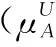


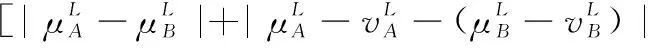

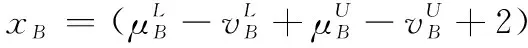
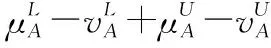
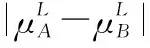
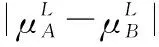
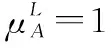

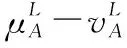

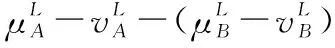
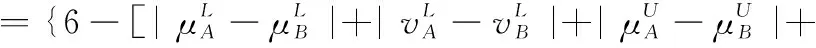
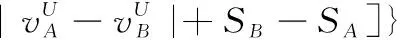
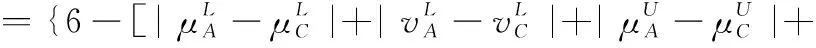
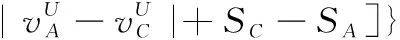
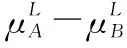
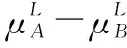
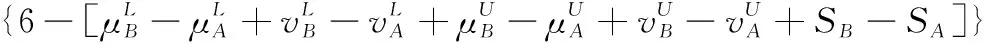
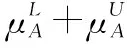
5 新的IVIFSs相似性分析与验证
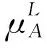
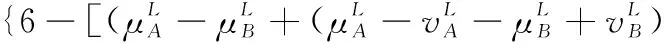
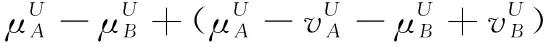
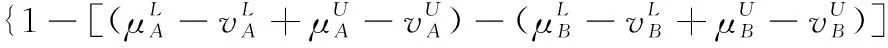
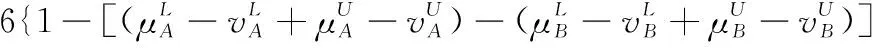
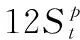
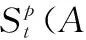
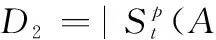

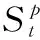
6 结 论
