刘芯菱，陈守全

(1.西华师范大学， 四川 南充 637002； 2.西南大学， 重庆 400715)

在学术界中，关于随机变量序列的极大值的渐近分布已经有了许多研究，假定第1个随机变量序列{ξn}为一个平稳的标准正态序列且具有相关系数ρj=Cov(ξ0,ξj)，第2个随机变量序列为一个独立标准正态序列，文献[1]证明了对于第一个序列，当条件

ρjlnj→0,j→∞

(1)

(1-ρnj)lnj→δj∈(0，∞]，j≥1

(2)

其中ρn, j=E(ξni,ξn,i+j)，δ0=0，可得到下面的引理。

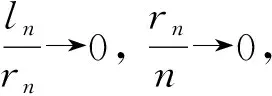
以及

那么

ϑexp(-x))

(3)

1 主要结论

αn,ln=max{|P(ξi≤un,i∈I∪J)-P(ξi≤un,i∈I)×P(ξi≤un,i∈J)|}

为混合系数，若当ln=o(n)时，αn,ln→0,n→∞，则称序列{ξn}满足Δ(un)条件。

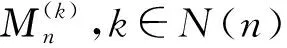
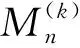
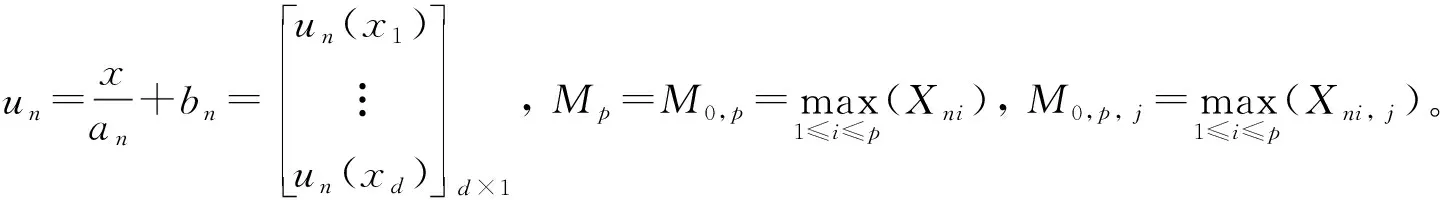
αn,ln=max{|P(Xi≤un,i∈I∪J)-P(Xi≤un,i∈I)×P(Xi≤un,i∈J)|}

为混合系数，若当ln=o(n)时，αn,ln→0,n→∞，则称序列{Xn}满足Δ(un)条件。

ϑjexp(-xj))

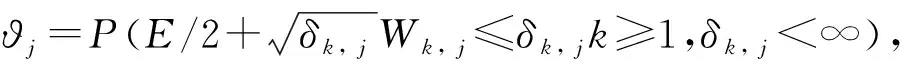
2 证明

为了证明主要结论，需要给出以下引理

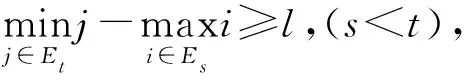
证明正如文献[2]中有关引理3.2.2的证明一样，将采用类似过程。为了简单起见令Ej={kj,…,lj}，若Δ(un)条件满足，且k2-l1≥l，则

|P(M(E1∩E2)≤un)-P(M(E1)≤un)×P(M(E2)≤un)|≤αn,l

类似地，结合E1∪E2⊂{k1,…,l2}和k3-l2≥l有

|P(M(E1∩E2∩E3)≤un)-P(M(E1)≤un)×P(M(E2)≤un)P(M(E3)≤un)|≤

|P(M(E1∩E2∩E3)≤un)-P(M(E1∩E2)≤un)P(M(E3)≤un)|+

|P(M(E1∩E2)≤un)P(M(E3)≤un)-P(M(E1)≤un)P(M(E2)≤un)P(M(E3)≤un)|≤2αn,l

重复以上过程，引理得证。

通过引理2，容易得到以下推论成立。

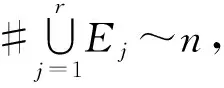
|P(Mn≤un)-Pr(Mp≤un)|→0,n→∞

证明由引理2得

|P(Mn≤un)-Pr(Mp≤un)|≤(r-1)αn,l

其中，

故得证。

引理3 令{Xni}为一个三角向量阵列，满足定理1中的条件①和条件②，则有

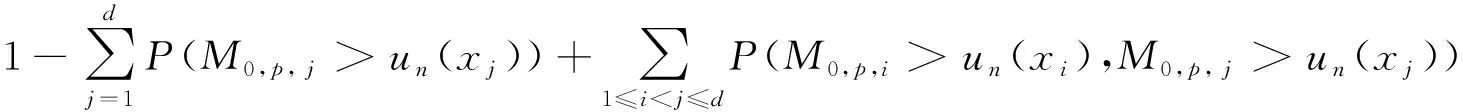
由平稳条件得

且

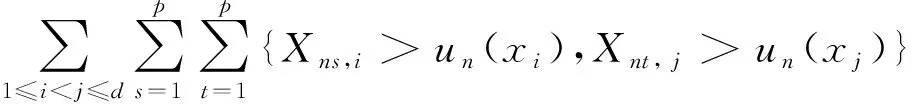
因此

P(Mn≤un)=Pr(Mp≤un)+o(1)≤(1-(B1-B2))r+o(1)≤

exp(-r(B1-B2))+o(1)

(4)

其中

(5)

以及

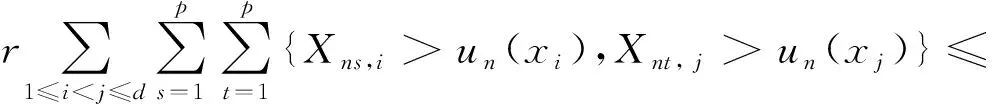
(6)

由式(4)～(6)得

(7)

下面只需要证明式(7)的反方向即可。因为

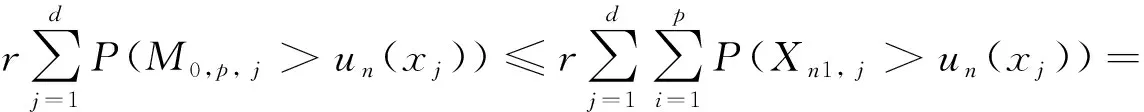
故存在常数C,C<∞，使得

r(1-P(Mp≤un))≤C

则有

只需证明，对于满足P(Mp≤un)收敛于Q∈[0,1]的某个子列，式(8)的反方向成立即可。

当Q=1，显然成立。

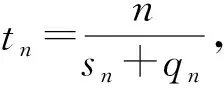
P(Mn, j≤un(xj))-Pr(M0,p, j≤un(xj))→0,n→∞

P(Mn, j≤un(xj))-Pt(M0,s, j≤un(xj))→0,n→∞

从而

Pr(M0,p, j≤un(xj))～Pt(M0,s, j≤un(xj))

记Ap, j={M0,p, j≤un(xj)}，则Pr(Ap)～Pt(As)，又因为当n→∞时，

所以

即有

P(M0,p, j>un(xj))=o(P(M0,s, j>un(xj))),j∈N(d)

从而

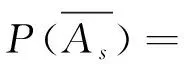
则有

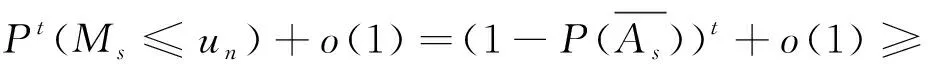
(8)

由式(8)有式(7)的反方向成立，结论得证。

定理1的证明对于三角阵列{Xni, j,j∈N(d)}，由引理3有

结合定理1中条件③有，引理1中条件满足，从而定理1得证。

3 结束语

本文将文献[4]中一类正态三角阵列的极限分布，通过运用概率极限理论的方法推广至有限维情形，具有一定的参考价值。