邱保志，程 栾

(郑州大学 信息工程学院，郑州 450001)

0 引言

聚类是将相似的数据对象聚集在一起，而相异的数据对象尽可能地分离[1]。聚类技术在数据挖掘、模式识别、图像处理、信息检索等领域有着广泛的应用，是数据分析的基础。在现有的聚类算法中，基于聚类中心的聚类算法由于其应用广泛而备受人们的关注，例如K-means[2]、具有噪声的基于密度的聚类方法(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)[3]、密度峰值聚类(Clustering by fast search and find of Density Peaks, DPC)算法[4]等，这些算法都是以选择初始聚类中心作为聚类的起始点，通过迭代或扩展进行聚类。选择聚类中心的准确性对聚类的迭代效率、聚类个数的确定和聚类精度有着重要的影响，如何准确地选择聚类中心、提高聚类精度成为聚类技术研究的关键问题。

以K-means为代表的基于划分的聚类首先初始化聚类中心，然后通过聚类中心的反复迭代的方式进行聚类，这类算法由于初始聚类中心选择的任意性，导致聚类结果精度不高；以DBSCAN为代表的基于密度聚类的算法是以任一个核心点作为聚类的起始点，将密度可达的对象集合看作一个聚类[5]，由于其中心点选择的随意性和密度定义的全局性，造成该类聚类算法不能对多密度数据集和高维数据集进行有效的聚类；基于密度峰值的聚类算法DPC以局部密度峰值为聚类中心，将包围密度峰值的低密度区域看成一个聚类[6-7]，虽然能准确地确定聚类的中心，但在确定密度峰值时需人工选取相应的参数，在没有先验知识的情况下，很难确定聚类的中心[8-9]。为了解决DPC算法存在的问题，拉普拉斯中心峰聚类(Laplace centrality Peaks Clustering, LPC)算法[10]将数据集转换为加权完全图，通过计算节点拉普拉斯中心性评估每个节点在加权图中的重要性，并计算一个节点到更高拉普拉斯中心性的节点的相对距离，将拥有较大拉普拉斯中心性且较大相对距离的对象确定为聚类中心，以此来进行聚类，但这一过程需要建立决策图人工选择聚类中心。

针对上述问题，本文通过引入图的拉普拉斯能量，综合考量每个节点的拉普拉斯中心性和该节点到具有更高拉普拉斯中心性的节点的相对距离，将数据集映射到由数据对象的拉普拉斯中心性和该对象的相对距离组成的二维特征空间中；进而构造决策图，依据正态分布的“3σ”准则提取聚类中心，从而自动确定聚类中心；最后将非聚类中心点指派到距离最近的数据对象所属聚类中，完成整个数据集的聚类。

1 相关定义

设数据集D={x1,x2,…,xn}，其中xi=(xi1,xi2,…,xim),i=1,2,…,n，m为数据对象的维度。用wi, j表示数据对象xi和xj之间的欧几里得距离，首先把数据集转换为加权完全图，数据集中每个数据对象作为图G中的一个节点，数据对象xi和xj之间的欧几里得距离作为图G中节点xi和xj之间边的权值。

定义1 相异度矩阵[10]。设加权完全图G是由数据集D转换得到的，则图G的相异度矩阵记为W(G)，定义如下：

(1)

其中，wi, j为节点xi和xj之间的欧几里得距离，对任意的1≤i，j≤n都有：wi, j≥0，wi, j=wj,i,wi,i=0。

Z(G)=diag(Z1,Z2,…,Zn)

(2)

定义3 拉普拉斯矩阵[10]。给定加权完全图G，它的拉普拉斯矩阵定义为:L(G)=Z(G)-W(G)。其中：Z(G)为图的和对角矩阵，W(G)为图的相异度矩阵。

定义4 拉普拉斯能量[11]。对于给定数据集D转换的加权完全图G，图G的拉普拉斯能量LEL(G)定义为其拉普拉斯矩阵的特征值的平方和，即：

(3)

其中,λ1,λ2,…,λn是图G的拉普拉斯矩阵L(G)的特征值。

定义5 拉普拉斯中心性[11]。给定加权完全图G，删除节点xi及其所有相连的边之后的图记为图Gi，给定xi∈G，节点xi的拉普拉斯中心性ci定义为：

ci=(LEL(G)-LEL(Gi))/LEL(G)

(4)

LEL(Gi)是删除节点xi之后图Gi的拉普拉斯能量。节点的重要性往往体现在该节点被移除之后对图的拉普拉斯能量的影响，因此可以用图中删除某节点后拉普拉斯能量的相对下降来度量一个节点的重要性(中心性)，拉普拉斯中心性越高，则该节点越重要。

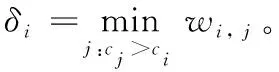
当数据对象xi为聚类中心时，ci和δi具有较大的值，令γi=ci*δi，这时，γi具有较大的值。为了从数据对象中分离出聚类中心，采用式(5)对γi进行放大[12]，加大聚类中心与其他数据对象的差别，从而便于识别真正的聚类中心。

(5)

定义7 正态分布[13]。若随机变量X服从一个数学期望为μ、标准差为σ的概率分布，且其概率密度函数为:

则这个随机变量X就称为正态随机变量，正态随机变量服从的分布就称为正态分布。

在正态分布中，随机变量X落在(μ-3σ，μ+3σ)以外的概率仅为0.002 7，基本上可以把区间(μ-3σ，μ+3σ)看作是随机变量X实际可能的取值区间，这称之为正态分布的“3σ”准则。

当数据对象xi为聚类中心时，该对象具有较高的拉普拉斯中心性ci和较大的相对距离δi两个特征。潜在聚类中心点所对应的E值远远大于非聚类中心点所对应的E值。由于聚类中心点拥有较大的E值，而非聚类中心点的E值较小这一特点，依据正态分布“3σ”准则筛选出那些E值大于μ+3σ的数据对象，将其设为聚类中心。图1是Sprial数据集所对应的分布直方图及其正态分布曲线。从图1中可以看出，Sprial数据集中有3个数据对象的E值大于μ+3σ，这3个数据对象就是数据集Sprial的3个类中心。

图1 数据集Sprial的分布直方图和正态分布曲线

2 ALPC描述

基于拉普拉斯中心性和密度峰值的无参数聚类算法(Parameter-free Clustering Algorithm based on Laplace centrality and density peaks, ALPC)首先把数据集转换为无向完全图G，得到图的拉普拉斯矩阵L(G)；然后根据删除某个数据对象后所引起的拉普拉斯能量变化，来得到数据对象的拉普拉斯中心性ci，并计算得到该数据对象的相对距离δi，接着通过式(5)扩大γ值之间的差别，通过正态分布，选取E值大于μ+3σ的数据对象为聚类中心,然后按照最近邻分类完成对整个数据集的聚类。ALPC算法描述如算法1所示。

算法1 ALPC。

输入 数据集D;

输出 聚类结果。

步骤1 将数据集D转换为带权完全图根据定义1～3计算W(G)、Z(G)和L(G)。

步骤2 根据式(3)、式(4)计算各数据对象的拉普拉斯中心性。

步骤3 提取数据集聚类中心：

a)根据定义6计算各数据对象的相对距离δi；

b)根据式(5)计算各数据对象的E值；

c)运用正态分布的3σ准则，将E值大于μ+3σ的数据对象作为聚类中心。

步骤4 按照最近邻分类完成对整个数据集的聚类。

在ALPC中，首先需要将待聚类的数据集转换为带权的无向完全图，图中的每个节点代表数据集中每个对象，利用拉普拉斯中心性来度量对象的重要性。拉普拉斯中心性基本思想是：通过删除某个节点后所引起的图的拉普拉斯能量的相对下降来度量该节点的中心性。然后计算该对象到具有更高拉普拉斯中心性的对象的相对距离，在聚类中心选取时，ALPC不再手动选取那些具有较大拉普拉斯中心性和较大相对距离的数据对象作为聚类中心，而是采用概率统计中正态分布理论选取聚类中心，避免了手动选取聚类中心时因视觉误差所带来的聚类结果的不准确问题。ALPC综合考虑对象的拉普拉斯中心性和该对象到更高拉普拉斯中心性的对象的相对距离，通过式(5)加大潜在聚类中心与待聚类数据集中其他对象的差别，利用概率统计中的正态分布理论选取具有较大E值，即E值大于μ+3σ的数据对象为聚类中心,然后按照最近邻分类原则将其余的点分配到相应的聚类中心，从而完成聚类并输出聚类结果。

3 实验结果与分析

该算法的实验环境为：CPU为AMD 3.4 GHz，4 GB内存，操作系统为Windows 7(64 bit)，算法的编写使用Matlab R2014a软件。

3.1 实验数据集及评价指标

实验选用 10个数据集，其中 4个人工数据集分别用于验证ALPC识别桥接簇、螺旋形、球形簇和非球形簇的能力；6个真实数据集来源于 UCI机器学习数据库，用于验证ALPC对高维数据处理的有效性。表1详细描述了实验数据集的基本信息。

表1 实验数据集基本信息

实验的评价指标采用准确率(ACCuracy, ACC)[10]、调整兰德系数(Adjusted Rand Index，ARI)[5]和归一化互信息(Normalized Mutual Information, NMI)[5]度量ALPC聚类的有效性。准确率衡量聚类结果与实际结果的符合程度，其取值范围为[0,1],当算法的聚类结果与真实情况完全一致时准确率为1，两者越不一致，准确率越低；调整兰德系数的计算需要待聚类数据集的真实分类结果，其取值范围为[-1,1]，调整兰德系数越高意味着算法的聚类结果与数据集的实际分类情况越吻合，从广义的角度看，调整兰德系数衡量的是算法聚类结果与数据集实际分类情况的吻合程度；归一化互信息是衡量聚类结果与数据集实际分类情况的相近程度，同样需要待聚类数据集的真实分类结果，归一化互信息的取值范围为[0,1]，值越大意味着聚类结果与真实情况越相近，聚类效果越好。

3.2 聚类结果分析

首先在二维数值属性数据集上与DBSCAN、DPC和LPC算法进行聚类有效性的比较，然后在高维数据集上与DBSCAN、DPC和LPC算法进行聚类有效性的比较。

图2依次是DBSCAN、DPC、LPC和ALPC在4k2_far、Aggregation、Spiral和Ring数据集上的聚类结果，不同的灰度值代表不同的聚类。

图2(a)是DBSCAN算法的聚类结果，它在Aggregation和Ring数据集上的聚类结果不正确，说明DBSCAN算法不能识别桥接簇和非球形簇，这是因为DBSCAN算法的半径阈值和密度阈值定义的全局性，当待聚类数据集的密度不均匀、聚类间距差很大时，参数选取困难，半径阈值和密度阈值选取不合适会造成聚类结果的不准确；图2(b)是DPC算法在4个人工数据集上的聚类结果，它在Ring数据集上的聚类结果不正确，这是因为DPC算法需要人工输入截断距离和手动选取聚类中心，截断距离定义的全局性和视觉误差造成的聚类中心选取不准确，就会影响聚类结果的准确性；图2(c)是LPC算法的聚类结果，它在4k2_far数据集上聚类结果不正确，这是因为LPC算法人为分析决策图，手动选取聚类中心时视觉误差造成的聚类中心选取不准确，使聚类结果不准确；图2(d)是算法ALPC的聚类结果，表明ALPC可以准确识别出数据集中的球形簇、桥接簇、螺旋形和非球形簇。上述四个二维数据集上的聚类结果验证了ALPC的有效性。

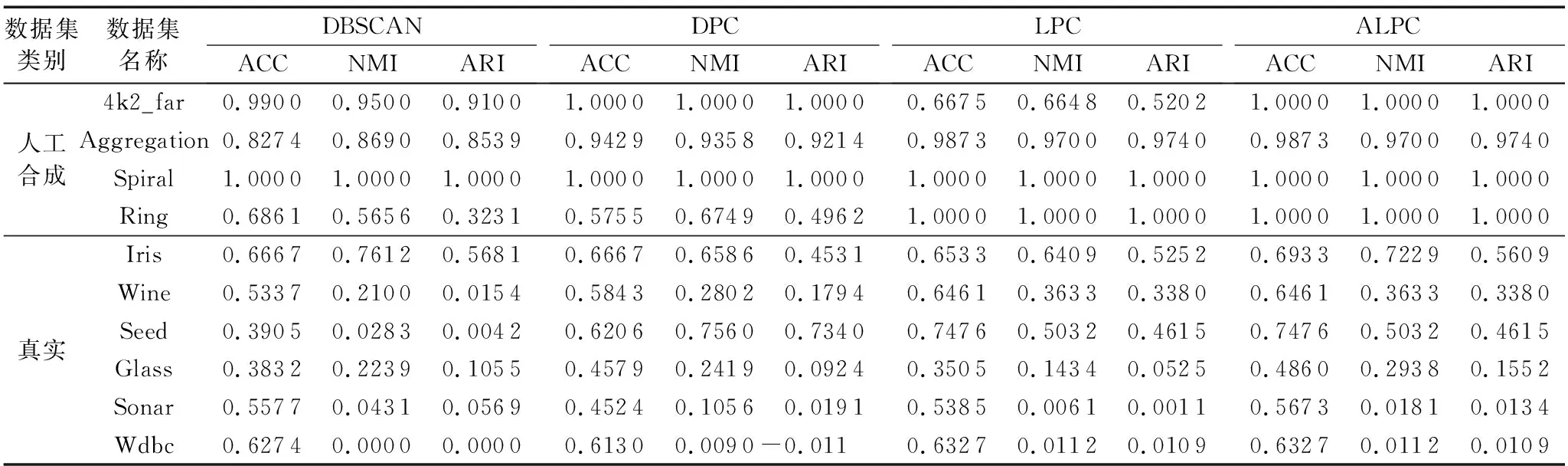
表2给出了4种算法在人工数据集和真实数据集上的实验结果。从表2中可以看出：与其他三个算法相比，ALPC的ACC值有10项为最高，NMI值有7项为最高，ARI值有7项为最高;虽然ALPC在Iris、Seed和Sonar这三个数据集上的归一化互信息和调整兰德系数不是最高值，但与评价指标最高值接近。

ALPC对于Spiral、Ring和4k2_far这三个数据集的执行能力最好，其聚类结果完全正确；与LPC算法相比较，ALPC在不需要人为干预的情况下对于Spiral、Aggregation、Ring、Wine、Seed和Wdbc这六个数据集自动划分的效果与人为划分效果一致，实现了自动聚类的目标；ALPC对4k2_far、Iris、Glass和Sonar这四个数据集自动划分的聚类结果的精度比LPC算法人为划分的聚类结果的精度要高，说明ALPC在应对一些数据集时，具有更优秀的性能，能得到较好的聚类效果。综上所述，ALPC对人工数据集和真实数据集均有良好的聚类结果。

3.3 时间复杂度分析

对于对象数量为n的数据集D:1)DPC算法的时间复杂度主要来自于距离矩阵、局部密度和相对距离的计算过程，其中计算距离矩阵和相对距离的时间复杂度为O(n2)，计算局部密度需要依次寻找与该对象相对距离小于截断距离的对象的时间复杂度最坏为O(n2)，所以DPC算法的时间复杂度为O(n2)。2)DBSCAN算法的时间复杂度为O(n2)；LPC算法的时间复杂度主要来自于距离矩阵、拉普拉斯中心性和相对距离的计算过程，其中计算距离矩阵和相对距离的时间复杂度为O(n2)，计算对象拉普拉斯中心性需要依次删除该对象并计算拉普拉斯能量的相对下降，时间复杂度最坏为O(n3)，所以LPC算法的时间复杂度为O(n3)。3)ALPC与LPC算法类似，所以ALPC算法的时间复杂度同样为O(n3)。

LPC算法不需要人工输入参数，但仍然需要人工选取聚类中心，虽然ALPC和LPC算法的时间复杂度相同，但ALPC可以自动选取聚类中心，避免了人工选取聚类中心的不准确问题。

图2 4种算法在人工数据集上聚类结果比较

数据集类别数据集名称DBSCANACCNMIARIDPCACCNMIARILPCACCNMIARIALPCACCNMIARI人工合成真实4k2_far0.99000.95000.91001.00001.00001.00000.66750.66480.52021.00001.00001.0000Aggregation0.82740.86900.85390.94290.93580.92140.98730.97000.97400.98730.97000.9740Spiral 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000Ring0.68610.56560.32310.57550.67490.49621.00001.00001.00001.00001.00001.0000Iris0.66670.76120.56810.66670.65860.45310.65330.64090.52520.69330.72290.5609Wine0.53370.21000.01540.58430.28020.17940.64610.36330.33800.64610.36330.3380Seed0.39050.02830.00420.62060.75600.73400.74760.50320.46150.74760.50320.4615Glass0.38320.22390.10550.45790.24190.09240.35050.14340.05250.48600.29380.1552Sonar0.55770.04310.05690.45240.10560.01910.53850.00610.00110.56730.01810.0134Wdbc0.62740.00000.00000.61300.0090-0.0110.63270.01120.01090.63270.01120.0109

4 结语

本文应用拉普拉斯理论和正态分布的“3σ”准则，提出了一种无参数聚类算法，实现了聚类中心的自动选择和无参数聚类，解决了LPC算法人工选取聚类中心的不准确性问题，为基于中心的聚类技术的聚类中心选取提供了理论基础，提高了聚类精度。

[4] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks [J]. Science, 2014, 344(6191): 1492-1496.

[5] 邱保志,唐雅敏.快速识别密度骨架的聚类算法[J].计算机应用,2017,37(12):3482-3486.(QIU B Z, TANG Y M. Efficient clustering algorithm for fast recognition of density backbone [J]. Journal of Computer Application, 2017, 37(12): 3482-3486.)

[6] 蒋礼青,张明新,郑金龙,等.快速搜索与发现密度峰值聚类算法的优化研究[J].计算机应用研究,2016,33(11):3251-3254.(JIANG L Q, ZHANG M X, ZHENG J L, et al. Optimization of clustering by fast search and find of density peaks [J]. Application Research of Computers, 2016, 33(11): 3251-3254.)

[7] 马春来,单洪,马涛.一种基于簇中心点自动选择策略的密度峰值聚类算法[J].计算机科学,2016,43(7):255-258.(MA C L, SHAN H, MA T. Improved density peaks based clustering algorithm with strategy choosing cluster center automatically [J]. Computer Science, 2016, 43(7): 255-258.)

[8] BIE R, MEHMOOD R, RUAN S S, et al. Adaptive fuzzy clustering by fast search and find of density peaks [J]. Personal and Ubiquitous Computing, 2016, 20 (5): 785-793.

[9] XU J, WANG G, DEND W. DenPEHC: density peak based efficient hierarchical clustering [J]. Information Sciences, 2016, 373(12): 200-218.

[10] YANG X H, ZHU Q P, HUANG Y J, et al. Parameter-free Laplacian centrality peaks clustering [EB/OL]. [2017- 12- 05]. https://www.researchgate.net/publication/320602767_Parameter-free_Laplacian_centrality_peaks_clustering.

[11] QI X, FULLER E, WU Q, et al. Laplacian centrality: a new centrality measure for weighted networks [J]. Information Sciences, 2012, 194(5): 240-253.

[12] YE X, LI D, HE X. An algorithm for automatic recognition of cluster centers based on local density clustering [C]// Proceedings of the 2017 29th Chinese Control and Decision Conference. Piscataway, NJ: IEEE, 2017: 1347-1351.

[13] STEIN C M. Estimation of the mean of a multivariate normal distribution [J]. Annals of Statistics, 1981, 9(6): 1135-1151.