福建省龙岩市第一中学 (364000)

刘文娟

圆锥曲线综合问题是解析几何的核心内容，是历年高考数学的重要考点之一，也是复习备考中较难突破的难点之一.对于圆锥曲线的综合问题，由于含字母且运算量大，加之学生能熟练使用的方法比较单一，所以在求解过程中让许多学生倍感困惑.在高考复习中，针对圆锥曲线的某些综合问题，不能仅仅停留在对问题的求解上，教师要善于适时引导学生对问题解决后的再研究、再发现.这样，既能培养学生的灵活解决数学问题的能力，又可以避免由于孤立静止地思考问题所带来思维的局限性和片面性，还能较好地激发学生自身对数学问题的探究能力，提升研究水平.这对于训练学生数学思维的敏捷性与灵活性是有益的.

笔者以下面的这道圆锥曲线综合问题为例，开启了抛物线中一个定点问题的探究之旅.

1.探究背景

笔者对学生的解答情况进行了分析，发现学生解题思路很好，只是未能到最终的结果.

思路2：先设M(-m,yM)、N(-m,yN)，写出以MN为直径的圆方程，同样联立直线方程x=ty+m与抛物线方程，得到一个一元二次方程，利用韦达定理得到y1+y2,y1·y2但由于忽略题目当中各变量间的关系，无法将圆方程继续整理化简，也放弃了.

笔者根据前面的解题思路继续讲评，正确解答：

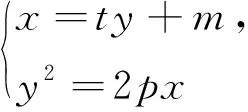
设M(-m,yM)、N(-m,yN)，则以MN为直径的圆方程(-m-x)2+(yM-y)(yN-y)=0，整理得x2+2mx+m2+y2-(yM+yN)y+yMyN=0，

令y=0，x2+2mx+m2+yMyN=0.

此题讲评完，学生感慨：看来“成功就是再坚持一下的努力中”真是没错.

课上，笔者又提问学生：反过来，我们是否能根据“以MN为直径的圆被x轴截得的弦长为定值

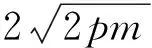
思考一段时间后，就有学生给出肯定答案，并根据刚才的推导过程，说明缘由.从而我们得到

讲完这道例题,笔者在想:是否还有其它的关于这个定点的等价条件?为完成教学进度,笔者课题上没有过多地思考,只给学生留下一句话:同学们把这道题作为一个特殊的题目记录在笔记中,课后有兴趣的同学可以交流探讨.但此时笔者的心中却已燃起了探究的火花.

2．探究发现

课后笔者再次探究这道题目时,突然想起在课本上有一道类似的题目,湖南教育出版社《数学》(选修1-1文科)第79页复习二第19题,也是探究抛物线中的定点问题.

设直线l与抛物线y2=2px(p>0)交于A(x1,y1),B(x2,y2)两点，其中y1>y2.

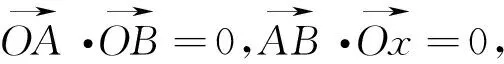
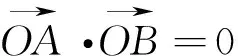
由这道例题，笔者再深入分析，发现这样一个更一般性的结论：

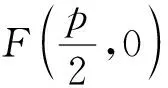
对于上面两道题的分析，给了笔者启发，在平时的教学过程中，做有心人，笔者又得到了其他几个结论.

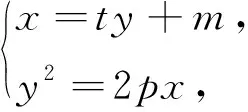
(充分性略)

结论4 设不垂直于x轴的直线l与抛物线y2=2px(p>0)交于A(x1,y1),B(x2,y2)两点，点M′(-m,0)，则直线l过点(m,0)(m>0)的充要条件是x轴为∠AM′B的角平分线.

结论5 设直线l与抛物线y2=2px(p>0)交于A(x1,y1),B(x2,y2)两点，则直线l过点(m,0)的充要条件是y1y2=-2pm.

还有下面两种特殊情况：

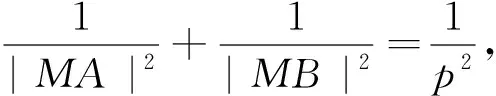
除了从结论1-结论5中得到直线过焦点的等价条件外，还有如下的结论：

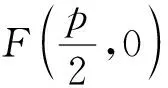
3.反思总结

教师在平时做题时，可以多做一些问题的拓展探究，并在讲题时适当引导学生思考探索，教师在教学中的多引导，促进学生多思考，培养学生的发散思维，让学生看到解题的“有趣”，体会数学的魅力.

在对抛物线中一个定点问题的探究过程中，给笔者的启发就是，我们要在平时的教与学的过程中做“有心人”，我们做的每一道题，都是专家经验的积累、智慧的结晶，所以不是做完一道题就结束了解题，我们要深入研究，也要引导学生利用好做过的题，善于积累将会起到事半功倍的作用，同时也可以挖掘学生的潜能，提高学习的兴趣.