杨 波

引言

切换系统是一类重要的混杂系统，它是由一族子系统和一个切换规律构成，该规则在某一时刻指定哪个子系统被激活.近年来,切换系统受到了越来越多的关注并取得了大量的研究成果.研究这种系统的主要动机包括以下两点.首先,从实际应用方面看,不同子系统之间的切换是许多实际系统的一个本质特征,例如,化工过程,运输系统,计算机控制系统和通讯工业等.其次,从控制观点看,多个控制器切换提供了一种有效的机制,可以处理具有大量不确定性和/或非常复杂的系统.例如,基于切换控制器的思想,研究者设计了一些智能控制方法以便于改进系统的性能.基于不同的工程背景,各类切换系统已被广泛研究,见文献[1-3]等.例如,文献[1]通过构造三重求和的Lyapunov泛函,研究了具有模式依赖无穷分布时滞的耦合中立性耦合神经网络的同步性问题.在文献[2]中,对具有不同类型激励函数和混合时滞的切换神经网络,作者给出了相应的被动性分析.

近来,通过驻留时间方法[4]探讨切换系统相关问题的研究兴趣已日益增加,并取得了一系列的研究成果.值得注意的是,时滞切换系统在工程系统中具有广阔的应用前景,例如,电力系统和网络化控制系统等,因此,一些研究人员已经着手研究时滞切换系统的性能.例如,文献[5]应用平均驻留时间方法给出了一类离散时间时滞切换系统达到指数稳定的充分条件.文献[6]应用比较原理和平均驻留时间技巧探讨了基因调控神经网络的随机稳定性问题.

此外,在设计时滞系统控制器时，我们期望闭环系统不仅稳定，而且具有足够的性能，尤其是当子系统之间存在切换现象的情况下.为了解决这一问题,我们可以考虑保成本控制，其主要思想是利用固定的李雅普诺夫函数给出二次成本函数关于闭环值的上界.目前,已有一些文献探讨了闭环系统的保证成本控制,见文献[7-11]等.例如,文献[7]考虑了一类具有脉冲的切换时滞系统,设计了它的鲁棒有限时间保成本控制问题.文献[11]针对具有中立型切换系统设计了具有动态输出反馈的保成本控制器.

以上这些研究结果主要关于线性时滞系统,设计相应的保成本控制器.然而,非线性时滞切换系统的保成本控制问题却被忽略,尽管这种控制问题在实际工程应用中非常重要.正是这一情形促使我们对这种系统的保成本控制问题展开研究.

在这篇文章中,我们通过状态反馈控制方法探讨了离散型的非线性时滞切换系统的保成本控制问题.借助平均驻留时间技巧和模式依赖的Lyapunov泛函方法,我们首先给出了保证所考虑的切换系统存在保成本控制器的充分条件及成本函数的上界.接着,我们由一族线性矩阵不等式的可行解表示了所需控制器的增益矩阵.

1 模型的刻画

考虑一类具有时滞的离散型切换非线性系统:

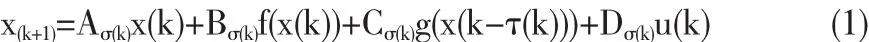
其中x(k)∈Rn是状态向量,其初始条件是x(l)=ø(l),k0-τ2≤l≤k0；f和 g：Rn→Rn是系统的非线性函数,u(k)∈Rn是控制输入信号.τ(k)表示有界的离散时滞,满足 τ1≤τ(k)≤τ2.{(Aσ(k)，Bσ(k)，Cσ(k)，Dσ(k))；σ(k)∈M,k≥k0}是一族矩阵,其中 M={1,2,…,m0},且σ:Z≥k0→M是分段常值函数,称为切换信号.

当σ(k)=i，i∈M时,对应于模式i的系统矩阵记为

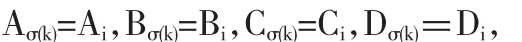
其中 Ai，Bi，Ci，Di是常矩阵.关于切换信号 σ,我们有切换序列

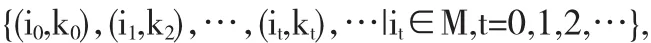
其中k0=0,这意味着当k∈[kt,kt+1)时,第it个子系统被激活.

假设1[1]设非线性函数f和g满足下面的扇形有界条件:

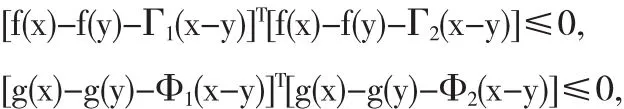
其中 Γ1，Γ2，Φ1，Φ2是适当维数的常值矩阵.

对于系统(1),我们考虑状态反馈控制,其控制输入为

其中Kσ(k)为需要设计控制增益矩阵.

由(1)和(2),我们可得到如下的切换闭环系统:

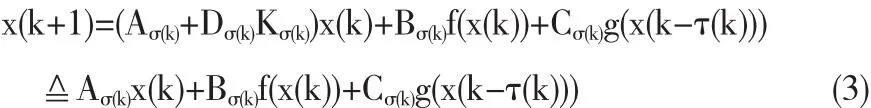
在本文中,我们对切换闭环系统(3)考虑保成本控制方法,并设成本函数为

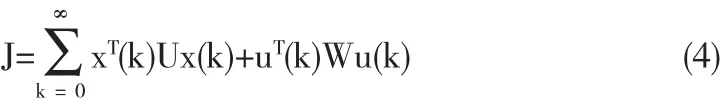
其中U和W为正定矩阵.

定义1[11]考虑切换非线性时滞系统(1).若存在状态反馈控制器u(k)和正常数J*使得闭环系统(3)是指数稳定的且成本函数J满足J≤J*,则J*称为保成本且u(k)称为切换系统(1)的保成本控制器.

在讨论上面的保成本控制问题之前,我们首先下面的定义.

定义2 系统(3)的平衡点x*=0是指数稳定的,若存在λ∈(0,1),ϑ＞0,使得(3)的解 x(k)满足

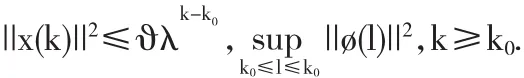
定义3[4]在区间[k0,k)上,切换信号σ的切换次数记为Nσ(k,k0).若存在 N0≥0 和 T0＞0 使得

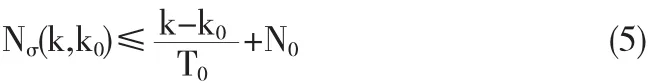
则T0称为平均驻留时间.为了简便,这里取N0=0.

本文的目的是对系统(3)设计保成本控制器u(k),使得闭环系统(3)是指数稳定的且成本函数J存在上界J*.

2 主要结果

在这一小节,我们将通过构造模式依赖的Lyapunov泛函,并应用平均驻留时间技巧给出闭环系统(3)和成本函数(4)存在保成本控制器(2)的充分条件;然后,借助一组线性矩阵不等式的可行解表示控制增益矩阵.

为此,我们考虑下面的无切换的非线性时滞系统:

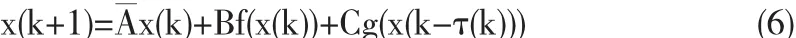
其中A=A+DK.

定理1 对给定的α∈(0,1)和增益矩阵K,若存在正定矩阵Q和R,使得下面的线性矩阵不等式成立

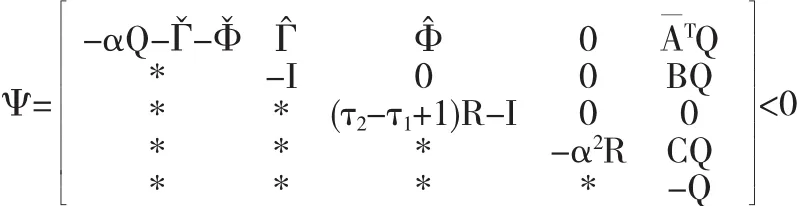
则系统(6)是指数稳定的.

证明 为了便于表示,我们记

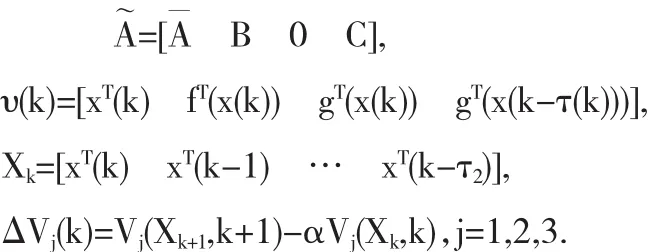
对于系统(6),我们构造如下的Lyapunov泛函:

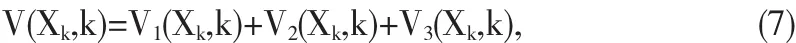
其中

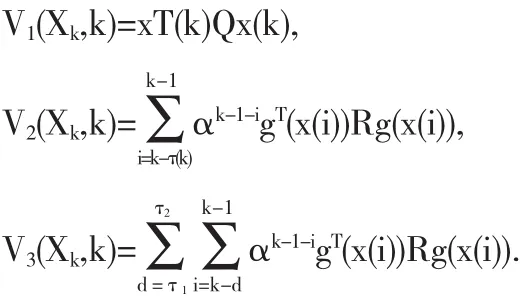
下面,我们计算Lyapunov泛函(7)关于系统(6)的差分:

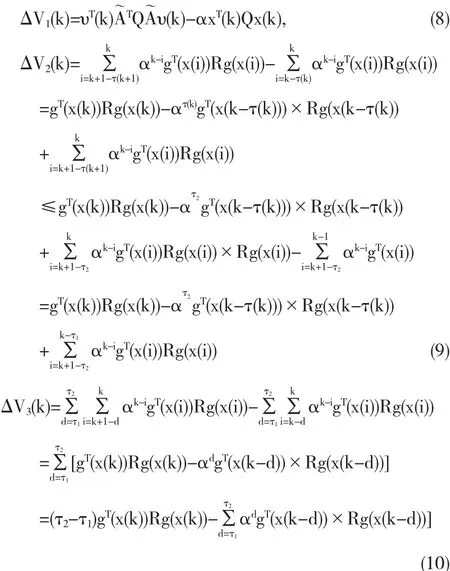
此外,由假设1可得

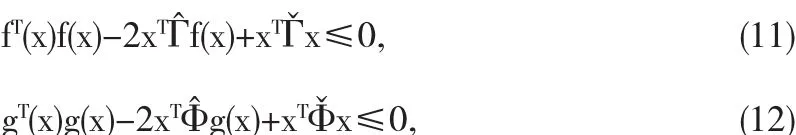
其中

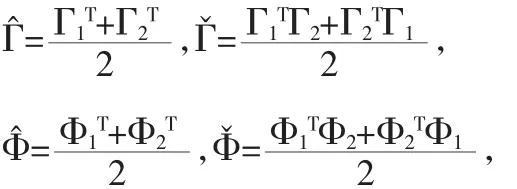
于是,由(8)-(12)可得,

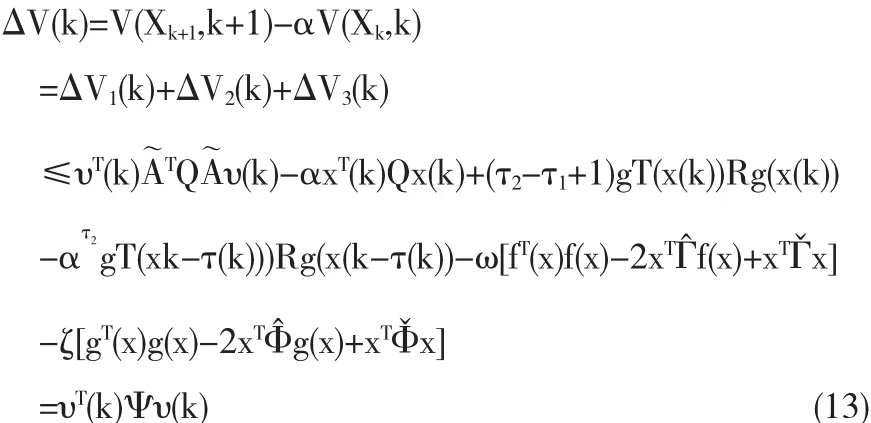
进一步,由条件Ψ＜0可知,

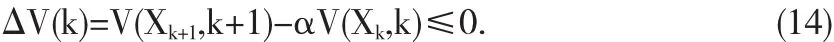
因此,当 k≥k0时,我们有

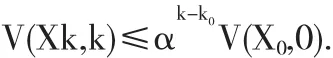
根据定义1,可知系统(6)是指数稳定的.证毕.

接下来,我们将在定理1的基础上,通过构造模式依赖的Lyapunov泛函,并应用平均驻留时间技巧给出系统(1)存在保成本控制器的充分条件.

定理2 对给定的α∈(0,1),μ＞1和增益矩阵Ki,若存在一组正定矩阵Qi和Ri,使得下面不等式成立

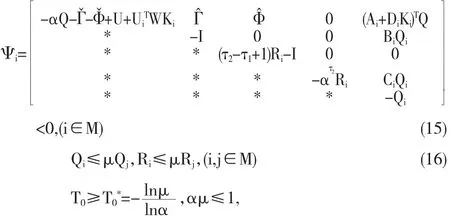
则控制器(2)是系统(1)的保成本控制器,且成本函数有如下的上界

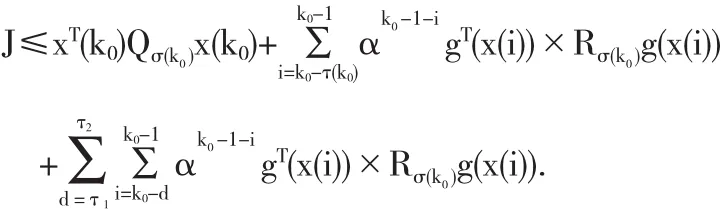
证明 构造模式依赖的Lyapunov泛函如下:

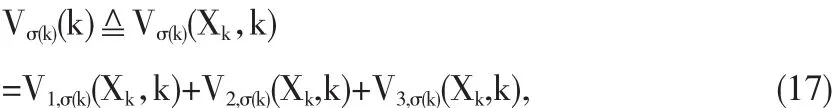
其中

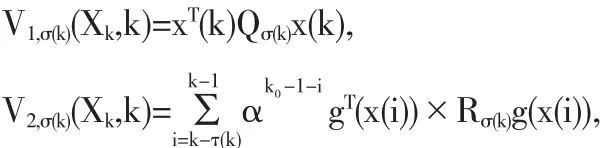
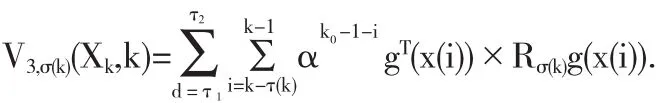
当k∈[kt,kt+1)时,应用定理1及条件(16),我们得到,

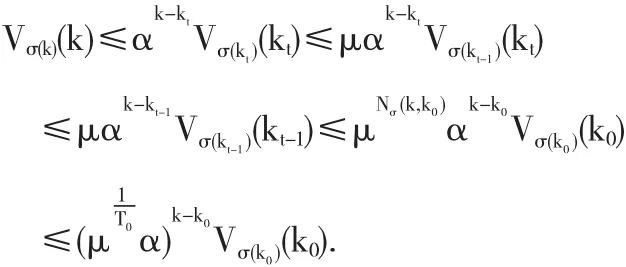
因此,由定义1可知,闭环系统(3)是指数稳定的.

另一方面,当 k∈[kt,kt+1)时,

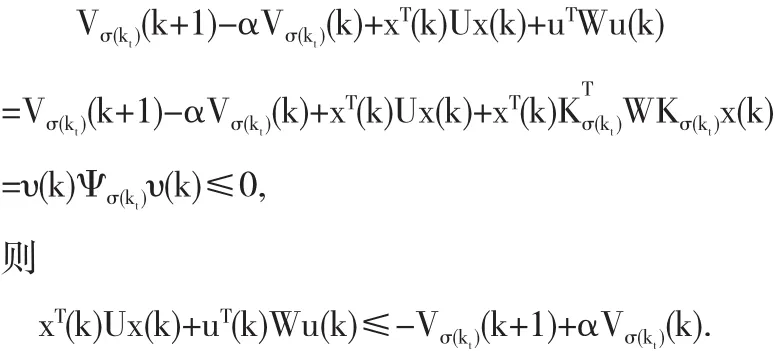
于是,我们得到

证毕.

定理2给出了系统(1)存在保成本控制器的充分条件及成本函数的上界.下面,我们将通过一组线性矩阵不等式的可行解表示出控制器的增益矩阵.

定理3 对给定的α∈(0,1),μ＞1,若存在一组正定矩阵Pi和Ri,使得下面不等式i∈M均成立.

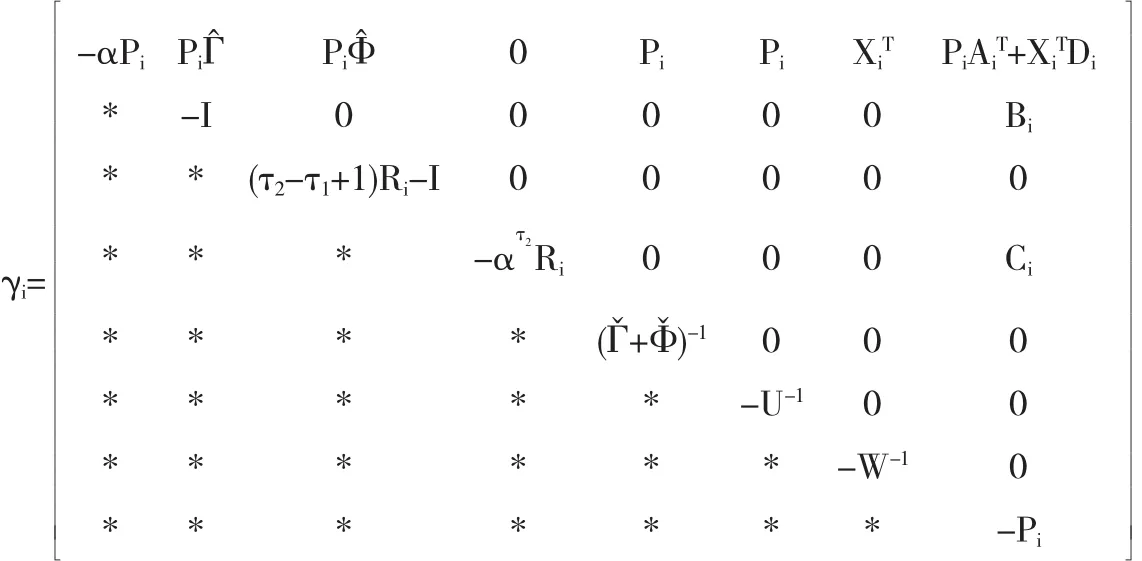
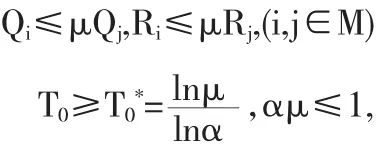
则控制器u(k)=Kix(k)且Ki=XiPi-1是系统(1)的保成本控制器,且成本函数J有如下的上界

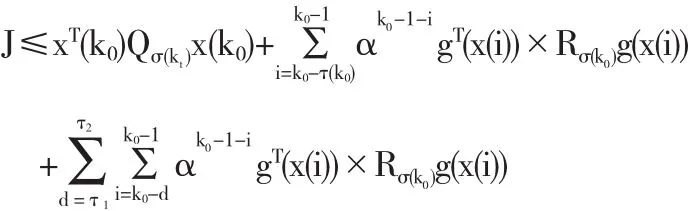
证明 现设Pi=Qi-1且Xi=KiPi,令Ξi=diag{PiI … I},则γi=ΞiTΩiΞi,其中

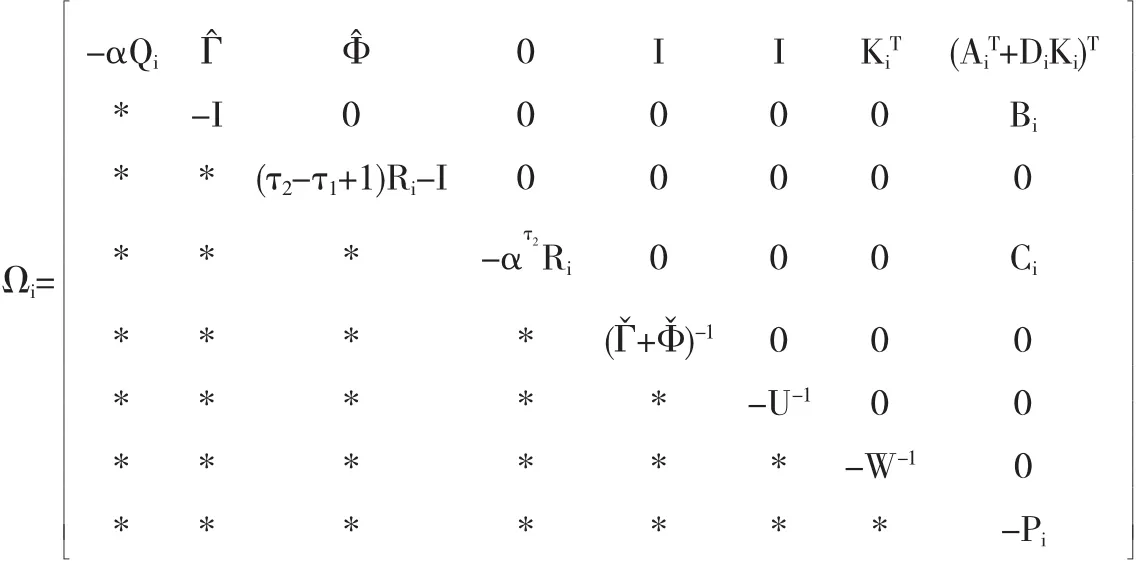
应用 Sucher Completement定理,可知 Ωi＜0等价于Ψi＜0,于是,由定理 2 可知结论成立.证毕.

3 结论

在这篇文章中,我们针对一类离散型切换系统探讨了它的保成本控制问题,其中既考虑了离散时滞又考虑了非线性函数对保成本控制问题的影响.我们通过构造模式依赖的Lyapunov泛函,并应用平均驻留时间技巧,给出了保成本控制器的充分条件,并给出了成本函数的上界.接着,借助一组线性矩阵不等式的可行解,我们表示了所需的保成本控制器的增益矩阵.